【抽代复习笔记】34-群(二十八):不变子群的几道例题
例1:证明,交换群的任何子群都是不变子群。
证:设(G,o)是交换群,H≤G,
对任意的a∈G,显然都有aH = {a o h|h∈H} = {h o a|h∈H} = Ha。
所以H⊿G。
【注:规范的不变子群符号是一个顶角指向左边的等腰三角形】
推论:
①循环群的子群都是不变子群;
②素数阶群的任何子群都是不变子群。
例2:证明,平凡子群是不变子群。
证:设(G,o)是一个群,则{e}和G本身是G的平凡子群。
①对∀a∈G,
显然a{e} = {a o e} = {a} = {e o a} = {e}a,
所以{e}是G的不变子群。
②下面证对∀a∈G,有aG = G = Ga:
对∀x∈G,有x = (a o a^(-1)) o x = a o (a^(-1) o x)∈aG,
即x∈aG,从而退出G⊆aG,又由aG的定义可知aG⊆G,所以G = aG,
同理可得Ga = G,
所以G⊿G。
例3:证明,设(G,o)是一个群,若N = {n∈G|n o a = a o n,a∈G},则N⊿G。
【这个不变子群称为G的中心,记作:C(G)。】
证:①对∀a∈G,有e o a = a = a o e,
所以e∈N,即N≠∅;
②∀n₁,n₂∈N,对∀a∈G,
有n₁ o a = a o n₁,n₂ o a = a o n₂,
所以(n₁ o n₂) o a = n₁ o (n₂ o a) = n₁ o (a o n₂) = (n₁ o a) o n₂ = (a o n₁) o n₂ = a o (n₁ o n₂),
所以n₁,n₂∈N;
③n₁^(-1) o a = (n₁^(-1) o a) o (n₁ o n₁^(-1)) = n₁^(-1) o (a o n₁) o n₁^(-1) = n₁^(-1) o (n₁ o a) o n₁^(-1) = (n₁^(-1) o n₁) o (a o n₁^(-1)) = a o n₁^(-1),
根据子群的第一判定定理,可得N≤G;
④由N的定义,易得aN = {a o n|n∈N} = {n o a|n∈N} = Na,
所以N⊿G。
例4:证明:
(1)K₄⊿A₄;
(2)N = {(1),(123),(132)}⊿S₃;
(3)H = {(1),(12)}不是S₃的不变子群。
证:(1)①因为K₄ = {(1),(12)(34),(13)(24),(14)(23)},
对∀a∈K₄,均有aK₄ = K₄a = K₄;
②因为(123)K₄ = K₄(123) = {(123),(134),(243),(142)},所以对∀a∈(123)K₄,有aK₄ = K₄a = (123)K₄;
③同②,因为(132)K₄ = K₄(132) = {(132),(143),(234),(124)},所以对∀a∈(132)K₄,有aK₄ = K₄a = (132)K₄,
同理可推出对∀a∈A₄,都有aK₄ = K₄a,
所以K₄⊿A₄。
(2)已知N是S₃的子群,运用(1)中同样的枚举法,易得对∀a∈S₃,有aN = Na,从而N⊿S₃。
(3)H = {(1),(12)}≤S₃,但对于(123)∈S₃,(123)H = {(123),(13)},而H(123) = {(123),(23)},即(123)H ≠ H(123),所以不满足不变子群的条件,
∴H不是S₃的不变子群。
[注:aN = Na并不是说a和N中的每一个元都适合交换律,而仅仅是作为集合它们是相等的。]
(待续……)
相关文章:
:不变子群的几道例题)
【抽代复习笔记】34-群(二十八):不变子群的几道例题
例1:证明,交换群的任何子群都是不变子群。 证:设(G,o)是交换群,H≤G, 对任意的a∈G,显然都有aH {a o h|h∈H} {h o a|h∈H} Ha。 所以H⊿G。 【注:规范的不变子群符号是一个顶角指向左边…...
Chrome和Firefox如何保护用户的浏览数据
在当今数字化时代,保护用户的浏览数据变得尤为重要。浏览器作为我们日常上网的主要工具,其安全性直接关系到个人信息的保密性。本文将详细介绍Chrome和Firefox这两款主流浏览器如何通过一系列功能来保护用户的浏览数据。(本文由https://chrom…...

CentOS 7镜像下载
新版本系统镜像下载(当前最新是CentOS 7.4版本) CentOS官网 官网地址 http://isoredirect.centos.org/centos/7.4.1708/isos/x86_64/ http://mirror.centos.org/centos/7/isos/ 国内的华为云,超级快:https://mirrors.huaweiclou…...

opencv-windows-cmake-Mingw-w64,编译opencv源码
Windows_MinGW_64_OpenCV在线编译动态库,并使用在C项目: (mingw-w64 cmakegithub actions方案) 修改版opencv在线编译: 加入opencv-contrib库, 一起编译生成动态库,在线编译好的opencv动态库,可以下载使用.验证opencv动态库是否可用的模板项目,测试opencv动态库是否可用的模板…...

Puppeteer点击系统:解锁百度流量点击率提升的解决案例
在数字营销领域,流量和搜索引擎优化(SEO)是提升网站可见性的关键。我开发了一个基于Puppeteer的点击系统,旨在自动化地提升百度流量点击率。本文将介绍这个系统如何通过模拟真实用户行为,优化关键词排名,并…...
Kyber原理解析
Kyber是一种IND-CCA2安全的密钥封装机制。Kyber的安全性基于在模格(MLWE问题)中解决LWE问题的难度。Kyber的构造采⽤两阶段⽅法:⾸先介绍⼀种⽤来加密固定32字节⻓度的消息原⽂的IND-CPA安全性的公钥加密⽅案,我们称之为 CPAPKE&a…...
2024 CCF CSP-J/S 2024 第二轮认证 真题试卷
2024年信息学奥赛CSP-J2入门级复赛真题试卷 题目总数:4 总分数:400 编程题 第 1 题 问答题 扑克牌(poker) 【题目描述】 小 P 从同学小 Q 那儿借来一副 n 张牌的扑克牌。 本题中我们不考虑大小王,此时每张牌具有两个属性:花色和…...

Android 无障碍服务常见问题梳理
android 无障碍服务本意是为了帮助盲人操作手机而设计,但是现在也有人利用这个做自动化操作。 本片文章讲述的主要用作自动化方面。 官方文档 关于配置方法和接口列表,参考 无障碍 比较常用的接口: 1. 执行点击操作 2. 触摸屏幕…...

Milvus 与 Faiss:选择合适的向量数据库
向量数据库 Milvus 和 Faiss 都是处理大规模向量数据的工具,尤其适用于需要相似性搜索的场景,比如推荐系统、图像检索和自然语言处理等。但它们各自的设计初衷和功能有所不同,适用于不同的使用场景。下面,我们从性能、功能特性、部…...

2024最全CTF入门指南、CTF夺旗赛及刷题网站(建议收藏!)
文章目录 一、赛事介绍二、竞赛模式三、CTF各大题型简介四、赛题情况分析CTF 工具集合Web | Web 安全🕸 MISC | 杂项❆ 基础工具❆ 解题工具❆ 开源脚本🔑 Crypto | 密码学 💫 Reverse | 逆向基础工具💥 PWN | 二进制 ὄ…...

【论文阅读】ESRGAN+
学习资料 论文题目:进一步改进增强型超分辨率生成对抗网络(ESRGAN : FURTHER IMPROVING ENHANCED SUPER-RESOLUTION GENERATIVE ADVERSARIAL NETWORK)论文地址:2001.08073代码:ncarraz/ESRGANplus: ICASSP …...
北京市首发教育领域人工智能应用指南,力推个性化教育新篇章
近年来,人工智能在全球教育领域的应用呈现蓬勃发展之势,各国都在探索如何将其更好的融入教育体系,在这一背景下,北京市于10月26日发布《北京市教育领域人工智能应用指南》(以下简称《指南》),推…...

【Java并发编程】信号量Semaphore详解
一、简介 Semaphore(信号量):是用来控制同时访问特定资源的线程数量,它通过协调各个线程,以保证合理的使用公共资源。 Semaphore 一般用于流量的控制,特别是公共资源有限的应用场景。例如数据库的连接&am…...
window11使用wsl2安装Ubuntu22.04
目录 1、快速了解wsl2 安装子系统linux流程(B站视频) 2、wsl2常用命令 3、windows与子系统Linux文件访问方法 4、子系统linux使用windows网络代理、网络配置(镜像网络,非NAT) 5、wsl2 Ubuntu miniconda 安装 6、…...
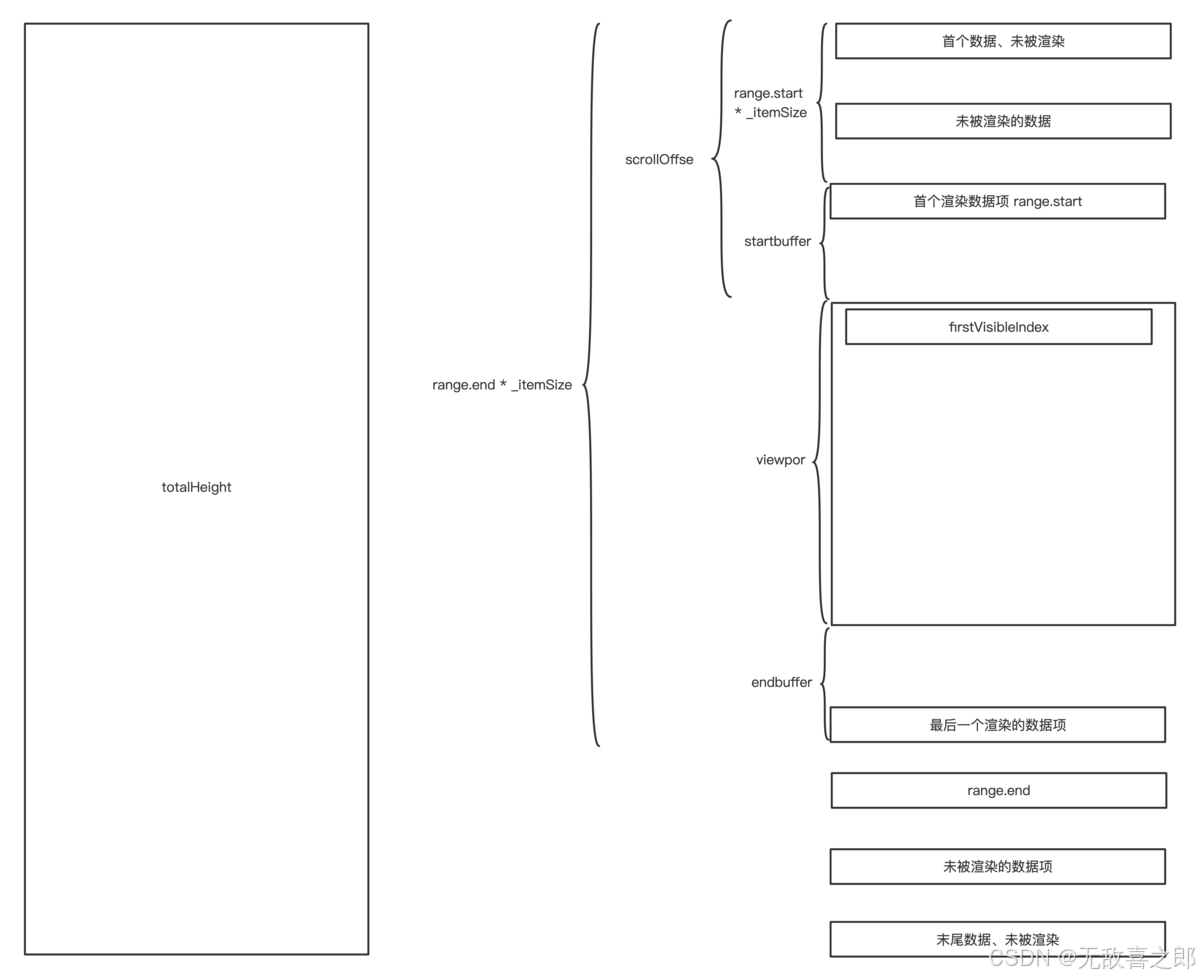
虚拟滚动 - 从基本实现到 Angular CDK
简介 在大数据列表的处理上,虚拟滚动是一种优化性能的有效方式。本篇文章将详细介绍两种常见的虚拟滚动实现方式:使用 transform 属性和 Intersection Observer。重点讲解如何通过 transform 属性实现高效的虚拟滚动,并对比Angular CDK中的实…...
)
Spring WebFlux学习笔记(一)
核心思想 WebFlux主要是异步 例子 参考一个源码: https://blog.csdn.net/qq_43923045/article/details/106309432?spm1001.2014.3001.5506 GetMapping("/delay1")public Mono<RestResult> delayResult() {long l System.currentTimeMillis();…...

富格林:正确追损思维安全交易
富格林指出,对于如何正确追损的这个问题是需要持续付出时间和精力的,发现具备耐心的投资者往往在正确追损的路上更加游刃有余。他们总是可以保持较为平和的心态,不急不躁地分析原因并通过自身掌握的安全应对措施来进行交易。富格林在以下分享…...

前端vue2迁移至uni-app
1.确定文件存放位置 components: 继续沿用 pages: views内容移动到pages static: assets内容移动到static uni_modules: uni-app的插件存放位置 迁移前 src├─assets│ └─less├─components│ ├─common│ │ ├─CommentPart│ │ └─MessDetail│ ├─home│…...

恋爱脑学Rust之闭包三Traits:Fn,FnOnce,FnMut
在Rust中,FnOnce、FnMut和Fn是三个用于表示闭包(closure)类型的trait。闭包是一种特殊的函数,它可以捕获其环境变量,即在其定义时所处的作用域中的变量。以下是关于这三个trait的详细介绍: 1. FnOnce&#…...

区块链介绍
区块链(英文名:blockchain或block chain)是一种块链式存储、不可篡改、安全可信的去中心化分布式账本,它结合了分布式存储、点对点传输、共识机制、密码学等技术,通过不断增长的数据块链(Blocks)…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
