空间解析几何【上】
文章目录
- 两向量共线&三向量共面
- 线段定比分点
- 内积&外积&混合积
- 内积(点积)
- 外积(叉积)
- 几何性质
- 混合积
- 轮换对称性
- 对换改变一次符号
- 线性性质
- 几何性质
- 球面方程
- 特点
- 空间平面
- 参数方程
- 行列式方程(点位式)
- 向量式方程
- 三点式方程
- 行列式方程
- 点法式
- 一般式
- 截距式
- 法式方程
- 离差
- 几何意义
- 两平面位置关系
- 相交
- 平行
- 重合
两向量共线&三向量共面
两向量 a ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_1, y_1, z_1) a=(x1,y1,z1), b ⃗ = ( x 2 , y 2 , z 2 ) \vec{b} = (x_2, y_2, z_2) b=(x2,y2,z2) 共线充要条件是对应坐标成比例,即
x 1 x 2 = y 1 y 2 = z 1 z 2 \frac{x_1}{x_2} = \frac{y_1}{y_2} = \frac{z_1}{z_2} x2x1=y2y1=z2z1
推论
三点 A ( x 1 , y 1 , z 1 ) A(x_1, y_1, z_1) A(x1,y1,z1), B ( x 2 , y 2 , z 2 ) B(x_2, y_2, z_2) B(x2,y2,z2), C ( x 3 , y 3 , z 3 ) C(x_3, y_3, z_3) C(x3,y3,z3) 共线充要条件
x 2 − x 1 x 3 − x 1 = y 2 − y 1 y 3 − y 1 = z 2 − z 1 z 3 − z 1 \frac{x_2 - x_1}{x_3 - x_1} = \frac{y_2 - y_1}{y_3 - y_1} = \frac{z_2 - z_1}{z_3 - z_1} x3−x1x2−x1=y3−y1y2−y1=z3−z1z2−z1
三非零向量 a ⃗ ( x 1 , y 1 , z 1 ) \vec{a}(x_1, y_1, z_1) a(x1,y1,z1), b ⃗ ( x 2 , y 2 , z 2 ) \vec{b}(x_2, y_2, z_2) b(x2,y2,z2), c ⃗ ( x 3 , y 3 , z 3 ) \vec{c}(x_3, y_3, z_3) c(x3,y3,z3) 共面充要条件
∣ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ∣ = 0 \left| \begin{array}{ccc} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{array} \right|= 0 x1x2x3y1y2y3z1z2z3 =0
四点 A i ( x i , y i , z i ) ( i = 1 , 2 , 3 , 4 ) A_i (x_i, y_i, z_i)\, ( i = 1, 2, 3, 4) Ai(xi,yi,zi)(i=1,2,3,4) 共面充要条件
∣ x 2 − x 1 y 2 − y 1 z 2 − z 1 x 3 − x 1 y 3 − y 1 z 3 − z 1 x 4 − x 1 y 4 − y 1 z 4 − z 1 ∣ = 0 \left| \begin{array}{ccc} x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\ x_3 - x_1 & y_3 - y_1 & z_3 - z_1 \\ x_4 - x_1 & y_4 - y_1 & z_4 - z_1 \end{array} \right| = 0 x2−x1x3−x1x4−x1y2−y1y3−y1y4−y1z2−z1z3−z1z4−z1 =0
或
∣ x 1 y 1 z 1 1 x 2 y 2 z 2 1 x 3 y 3 z 3 1 x 4 y 4 z 4 1 ∣ = 0 \left| \begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \end{array} \right|= 0 x1x2x3x4y1y2y3y4z1z2z3z41111 =0
线段定比分点
设空间两点 P 1 ( x 1 , y 1 , z 1 ) P_1(x_1, y_1, z_1) P1(x1,y1,z1) 和 P 2 ( x 2 , y 2 , z 2 ) P_2(x_2, y_2, z_2) P2(x2,y2,z2),点 P ( x , y , z ) P(x, y, z) P(x,y,z) 在 P 1 P 2 P_1 P_2 P1P2 两点连线上按比例 λ \lambda λ 分割线段 P 1 P 2 P_1 P_2 P1P2 的点 P P P,即
P 1 P P P 2 = λ \frac{P_1 P}{P P_2} = \lambda PP2P1P=λ
其中,
{ λ > 0 ( P ∈ P 1 P 2 ) λ < 0 ( P ∉ P 1 P 2 ) \begin{cases} \lambda > 0 & (P\in P_1 P_2 ) \\ \lambda < 0 & (P\notin P_1 P_2 ) \end{cases} {λ>0λ<0(P∈P1
相关文章:

空间解析几何【上】
文章目录 两向量共线&三向量共面线段定比分点内积&外积&混合积内积(点积)外积(叉积)几何性质混合积轮换对称性对换改变一次符号线性性质几何性质球面方程特点空间平面参数方程行列式方程(点位式)向量式方程三点式方程行列式方程点法式一般式截距式法式方程离…...

Python 获取PDF的各种页面信息(页数、页面尺寸、旋转角度、页面方向等)
目录 安装所需库 Python获取PDF页数 Python获取PDF页面尺寸 Python获取PDF页面旋转角度 Python获取PDF页面方向 Python获取PDF页面标签 Python获取PDF页面边框信息 了解PDF页面信息对于有效处理、编辑和管理PDF文件至关重要。PDF文件通常包含多个页面,每个页…...

独孤思维:曾经副业赚大钱的人,怎么不见了
01 总有一双眼睛默默关注你。 别以为自己每天做项目,日更文章,没人看。 总会有人默默观察你。 看你能坚持多久,看多段时间,你是不是还在。 今天上午,有个2年前认识的副业同行,今天突然跟我发消息。 说…...

OpenGL 异常处理-glCreateShader失败
【1】glCreateShader创建顶点着色器时候报错,如下 【2】原因分析 初始化失败,你使用一个扩extension loader library来访问现代OpenGL,当需要初始化它时,加载器需要一个当前的上下文来加载 【3】解决办法 GLenum glew_err gle…...

【el-pagination的使用及修改分页组件的整体大小修改默认样式的宽度详细教程】
今天遇到个bug,使用element-puls中的分页的时候,长度会超出盒子,今天教大家如何修改el-pagination的宽度,以及修改分页组件的整体大小 直接修改 style"width: 100%; margin-top: 10px"不生效 控制台修改el-pagination…...

Uniapp的学习
uniapp的内容和vue网页开发会有很多区别,但是都是基于vue开发的,大多数业务还是在vue打交道,但是这些uniapp的特殊的知识点也是要掌握好的。 基本配置 创建uniapp项目 npx degit dcloudio/uni-preset-vue#vite-ts 项目名 :用于…...

C#-万物之父object、装箱拆箱
万物之父:object 基于里氏替换原则,可以用object容器装载一切类型的变量。可以用来表示不确定类型,作为函数参数类型 object是所有类型的基类 装箱拆箱 用object存值类型(装箱)→ 把值类型用引用类型存储,…...

AI大模型重塑软件开发流程:从自动化编码到智能协作的未来展望
目录 1. 引言:AI大模型的崛起与软件开发的变革 1.1 AI大模型的兴起与发展背景 1.2 软件开发的现状与痛点 1.3 AI大模型如何解决这些问题 2. AI大模型的工作原理与技术背景 2.1 什么是AI大模型? 2.2 深度学习与自然语言处理技术的演变 2.3 大模型…...

HTB:GreenHorn[WriteUP]
目录 连接至HTB服务器并启动靶机 使用nmap对靶机TCP端口进行开放扫描 再次使用nmap对这三个端口进行脚本、服务扫描 尝试先通过curl访问靶机80端口 将靶机IP与该域名写入hosts使DNS本地解析 使用浏览器访问greenhorn.htb 使用Wappalyzer插件查看该页面技术栈 尝试在sea…...

SelfAttention在Ascend上的实现
1 SelfAttention是什么? Self-Attention(自注意力)机制是深度学习领域的一种重要技术,尤其在自然语言处理(NLP)任务中得到广泛应用。它是 Transformer 架构的核心组成部分之一,由 Vaswani 等人…...

C#设计模式
文章目录 项目地址一、开放封闭原则1.1 不好的版本1.2 将BankProcess的实现改为接口1.3 修改BankStuff类和IBankClient类二、依赖倒置原则2.1 高层不应该依赖于低层模块2.1.1 不好的例子2.1.2 修改:将各个国家的歌曲抽象2.2 抽象不应该依于细节2.2.1 不同的人开不同的车(接口…...

仪表板展示|DataEase看中国:历年双十一电商销售数据分析
背景介绍 2024年“双十一”购物季正在火热进行中。自2009年首次推出至今,“双十一”已经成为中国乃至全球最大的购物狂欢节,并且延伸到了全球范围内的电子商务平台。随着人们消费水平的提升以及电子商务的普及,线上销售模式也逐渐呈现多元化…...

急着骂华为?我劝你别急
文 | AUTO芯球 作者 | 雷慢 赛力斯这下怒了! 要对那些华为黑、问界黑出手了, 就在这几天,赛力斯起诉了一批蓄意抹黑、散步虚假信息的人。 起因是什么,听我慢慢说, 今年7月,佛山一辆问界M7发生交通事故…...
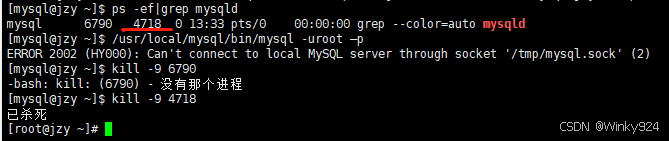
虚拟机linux7.9下安装mysql
1.MySQL官网下载安装包: MySQL :: Download MySQL Community Server https://cdn.mysql.com/archives/mysql-5.7/mysql-5.7.39-linux-glibc2.12-x86_64.tar.gz 2.解压文件: #tar xvzf mysql-5.7.39-linux-glibc2.12-x86_64.tar.gz 3.移动文件&#…...

【Linux】一篇文章轻松搞懂基本指令
本篇所有展示代码均是在超级用户的权限下进行的,如果不是超级用户并且一些命令执行的和我的不太一样,那么可以试着在对应命令前暂且加上sudo,我们在下一篇会讲权限问题,到时候再转换为普通用户。 本篇展示的内容是基于CentOs进行…...

深入浅出理解Spring和SpringBoot,剖析自动配置源码
文章目录 1.Spring2.SpringBoot3.小结 1.摘要 本文旨在带大家理解Spring框架和SpringBoot框架最为核心的部分,自Spring和SpringBoot问世以来,给Web开发掀起了巨大的浪潮,极大的缩短项目开发周期,下面将带大家分析Spring和SpringBo…...
)
Spring配置文件初始化加载(一)
1.枚举 public enum TestEnum {type_01("01", "zeroTest01ServiceImpl"),type_02("02", "zeroTest02ServiceImpl"),type_03("03", "zeroTest03ServiceImpl");private String type;private String pathClass; } …...

正则表达式 - 简介
正则表达式 - 简介 正则表达式(Regular Expression,简称Regex)是一种用于处理字符串的强大工具,它允许用户通过特定的模式(pattern)来搜索、匹配、查找和替换文本中的数据。正则表达式广泛应用于文本编辑器…...

【电机控制器】STC8H1K芯片——ADC电压采集
【电机控制器】STC8H1K芯片——ADC电压采集 文章目录 [TOC](文章目录) 前言一、ADC1.ADC初始化1.ADC_CONTR2.ADCCFG3.ADCTIM4.代码 2.ADC读取1.ADC_RES、ADC_RESL2.代码 3.VREF电压读取——MCU工作电压1.MCU工作电压计算公式2.代码 4.ADC被转换通道的输入电压读取1.ADC被转换通…...

图像格式中的 stride 和 pix stide
最近发现media codec 解码后 yuv 的拷贝时间很大,进一步分析后发现底层会一个像素一个像素拷贝,非常花时间。用过调整解码后图像的Stride(步幅)后直接进行内存块拷贝,可以大幅缩短拷贝时间 在YUV图像格式中,…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
