求从2开始的第n个素数
方法一:暴力法
-
思路:从2开始,逐个判断每个数是否为素数。素数是除了1和它自身外,不能被其他自然数整除的数。对于每个数
m,从2到sqrt(m)遍历,如果能被整除则不是素数。当找到n个素数时停止。 -
C++ 代码如下:
#include <iostream>
#include <cmath>
using namespace std;bool isPrime(int num) {if (num <= 1) return false;if (num <= 3) return true;if (num % 2 == 0 || num % 3 == 0) return false;/*for (int i = 5; i * i <= num; i = i + 6) {if (num % i == 0 || num % (i + 2) == 0) return false;}*/for(int i=5;i*i<=num;i++){if(num%i==0) return false;}return true;
}int nthPrime(int n) {int count = 0;int num = 2;while (true) {if (isPrime(num)) {count++;if (count == n) return num;}num++;}return -1;
}int main() {int n;cout << "Enter the value of n: ";cin >> n;cout << "The " << n << "th prime number is: " << nthPrime(n) << endl;return 0;
}
方法二:埃氏筛法(Sieve of Eratosthenes)改进
-
思路:先创建一个足够大的布尔数组来标记数是否为素数。从2开始,将2的倍数标记为非素数,然后找到下一个未标记的数(即素数),重复这个过程。当找到
n个素数时,可以得到第n个素数的值。 -
C++ 代码如下:
#include <iostream>
#include <vector>
using namespace std;int nthPrime(int n) {if (n == 1) return 2;int scope = 100;int x = (int)(scope / log(scope));while (x < n) {scope++;x = (int)(scope / log(scope));}cout<< "scope: " << scope << endl;vector<bool> isPrime(scope, true); // 假设一个较大的范围,可根据需要调整//vector<bool> isPrime(1000000, true); // 假设一个较大的范围,可根据需要调整isPrime[0] = isPrime[1] = false;int count = 0;for (int i = 2; i < isPrime.size(); i++) {if (isPrime[i]) {count++;if (count == n) return i;for (int j = i * i; j < isPrime.size(); j += i) {isPrime[j] = false;}}}return -1;
}int main() {int n;cout << "Enter the value of n: ";cin >> n;cout << "The " << n << "th prime number is: " << nthPrime(n) << endl;return 0;
}
这两种方法中,埃拉托斯特尼筛法在处理较大的n值时效率更高,因为它避免了对许多数的重复判断。但需要注意内存使用情况,如果n非常大,可能需要更复杂的数据结构或算法优化。
拓展与总结:
-
从不大于 n 的自然数随机选一个,它是素数的概率大约是 1 / l n ( n ) 1/ln(n) 1/ln(n)。
所以范围为n以内的素数个数为 n / l n ( n ) n/ln(n) n/ln(n) ,在n->无穷时成立,其他情况下近似成立。 -
比如求第100个素数,设num的范围是x,则必须满足 x / l n ( x ) > = 100 x/ln(x)>=100 x/ln(x)>=100 ,解出的这个x才是我们需要的范围,在这个范围内我们才能找到第100个素数。
相关文章:

求从2开始的第n个素数
方法一:暴力法 思路:从2开始,逐个判断每个数是否为素数。素数是除了1和它自身外,不能被其他自然数整除的数。对于每个数m,从2到sqrt(m)遍历,如果能被整除则不是素数。当找到n个素数时停止。 C 代码如下&am…...

【Android】View—基础知识,滑动,弹性滑动
基础知识 什么是View 在 Android 中,View 是用户界面(UI)中的基本组件,用于绘制图形和处理用户交互。所有的 UI 组件(如按钮、文本框、图片等)都是 View 的子类。可以说,View 是构建 Android …...

MYSQL中的两种转义操作
在 MySQL 中,转义字符用于处理特殊字符,以防止语法错误或 SQL 注入攻击,而单双引号都是需要重点注意的字符 可以用转义符\ 和 两个连续的引号 来起到转义引号的作用 转义符转义: 这是users表中的数据 如果查询admin 或者 admin" 用户,可以用转义符\ 两个连…...
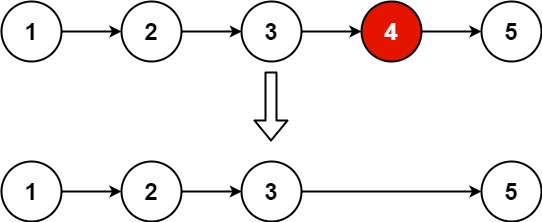
力扣题目解析--删除链表的倒数第n个节点
题目 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
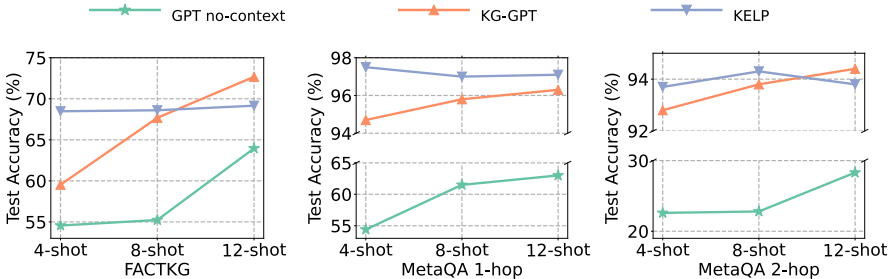
Knowledge Graph-Enhanced Large Language Models via Path Selection
研究背景 研究问题:这篇文章要解决的问题是大型语言模型(LLMs)在生成输出时存在的事实不准确性,即所谓的幻觉问题。尽管LLMs在各种实际应用中表现出色,但当遇到超出训练语料库范围的新知识时,它们通常会生…...

Android 项目模型配置管理
Android 项目配置管理 项目模型相关的配置管理config.gradle文件:build.gradle文件: 参考地址 项目模型相关的配置管理 以下是一个完整的build.gradle和config.gradle示例: config.gradle文件: ext {// 模型相关配置࿰…...

「QT」几何数据类 之 QSizeF 浮点型尺寸类
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid…...

Essential Cell Biology--Fifth Edition--Chapter one(2)
1.1.1.3 Living Cells Are Self-Replicating Collections of Catalysts 催化剂集合 生物最常被引用的特性之一是它们的繁殖能力。对于细胞来说,这个过程包括复制它们的遗传物质和其他成分,然后分裂成两个,产生一对子细胞[daughter cells]&a…...
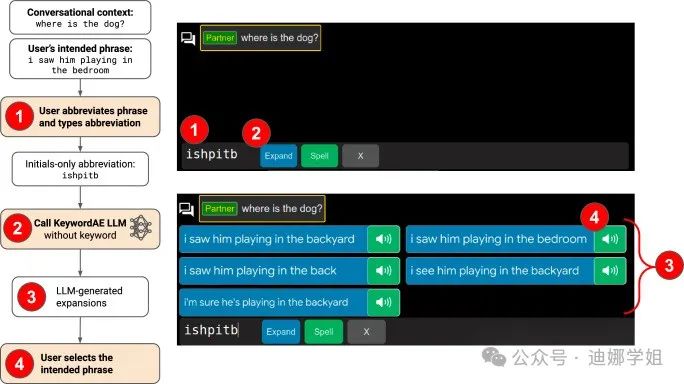
大语言模型LLMs在医学领域的最新进展总结
我是娜姐 迪娜学姐 ,一个SCI医学期刊编辑,探索用AI工具提效论文写作和发表。 相比其他学科,医学AI,是发表学术成果最多的领域。 医学数据的多样性和复杂性(包括文本、图像、基因组数据等),使得…...

云防护单节点2T抗攻击能力意味着什么?
随着互联网的发展,DDoS攻击的规模和频率不断增加,对企业和个人用户的网络服务造成了严重威胁。云防护服务作为一种高效的DDoS防护手段,逐渐成为许多企业的首选。本文将重点讨论云防护单节点2T(太比特每秒)抗攻击能力的…...

IDEA在编译时: java: 找不到符号符号: 变量 log
一、问题 IDEA在编译的时候报Error:(30, 17) java: 找不到符号符号: 变量 log Error:(30, 17) java: 找不到符号 符号: 变量 log 位置: 类 com.mokerson.rabbitmq.config.RabbitMqConfig 二、解决方案 背景:下载其他同事代码时,第一次运行,…...

HTML 基础架构:理解网页的骨架
HTML的文档结构主要由以下几个部分组成:<html>、<head>和<body>。 <html>标签是HTML文档的根元素,用来包裹整个HTML文档的内容。<head>标签用于定义文档的头部,包含了一些元数据和其他不直接显示在页面上的内…...

FPGA学习笔记#5 Vitis HLS For循环的优化(1)
本笔记使用的Vitis HLS版本为2022.2,在windows11下运行,仿真part为xcku15p_CIV-ffva1156-2LV-e,主要根据教程:跟Xilinx SAE 学HLS系列视频讲座-高亚军进行学习 从这一篇开始正式进入HLS对C代码的优化笔记 目录 1.循环优化中的基…...

web实操4——servlet体系结构
servlet体系结构 我们基本都只实现service方法,其余几个都不用, 之前我们直接实现servlet接口,所有的方法都必须实现,不用也得写,不然报错,写了又不用当摆设。 能不能只要定义一个service方法就可以&…...

Linux开发讲课48--- Linux 文件系统概览
本文旨在高屋建瓴地来讨论 Linux 文件系统概念,而不是对某种特定的文件系统,比如 EXT4 是如何工作的进行具体的描述。另外,本文也不是一个文件系统命令的教程。 每台通用计算机都需要将各种数据存储在硬盘驱动器(HDD)…...

Node.js 模块详解
模块的概念 Node.js 运行在 V8 JavaScript 引擎上,通过 require() 函数导入相关模块来处理服务器端的各种进程。一个 Node.js 模块可以是一个函数库、类集合或其他可重用的代码,通常存储在一个或多个 .js 文件中。 例如,启动一个 Node.js 服…...

大厂面试真题-说说tomcat的优缺点
Tomcat作为服务器,特别是作为Java Web服务器,具有一系列优点和缺点。以下是对其优缺点的详细分析: 优点 开源免费: Tomcat是一个免费、开源的Web服务器,用户可以在任何环境下自由使用,无需支付任何费用。…...

Linux系统编译boot后发现编译时间与Windows系统不一致的解决方案
现象 如下图,从filezilla软件看虚拟机Linux中编译的uboot.img修改时间与Windows系统时间不同 解决过程 在Linux中查看编译的uboot详细信息,从而得到编译时间。终端输入ls -l后,如下图: 结论 说明在Linux是按照Windows系统时…...

WPS Office手机去广高级版
工具介绍功能特点 WPS Office是使用人数最多的移动办公软件,独有手机阅读模式,字体清晰翻页流畅;完美支持文字,表格,演示,PDF等51种文档格式;新版本具有海量精美模版及高级功能 安装环境 [名称…...

Python爬虫基础-正则表达式!
前言 正则表达式是对字符串的一种逻辑公式,用事先定义好的一些特定字符、及这些特定字符的组合,组成一个“规则的字符串”,此字符串用来表示对字符串的一种“过滤”逻辑。正在在很多开发语言中都存在,而非python独有。对其知识点…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
