【Python-AI篇】K近邻算法(KNN)
0. 前置----机器学习流程
- 获取数据集
- 数据基本处理
- 特征工程
- 机器学习
- 模型评估
- 在线服务
1. KNN算法概念
如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中大多数属于某一个类别,则该样本也属于这一个类别
1.1 KNN算法流程总结
- 计算已知类别数据集中的点与当前点之间的距离
- 按距离递增次序排序
- 选取与当前点距离最小的k个点
- 统计前k个点所在的类别出现的频率
- 返回前k个点出现频率最高的类别作为当前点的预测分类
2. KNN算法api ---- Scikit-learn
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, algorithm='auto')
参数含义:
- n_neighbors: 查询默认使用的邻居数,默认为5
- algorithm:
- 快速K近邻搜索算法,默认参数为auto,可以理解为算法自己决定合适的搜索算法,除此之外,用户也可以自己指定搜索算法进行搜索
- bruth: 蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时
- kd_tree: 构造kd树存储数据以便对其进行快速搜索的树形数据结构,kd树也就是数据结构
- ball_tree: 为了克服kd树高维失效而发明的,其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体
简单示例:
from sklearn.neighbors import KNeighborsClassifier# 构造数据集
x = [[0], [1], [2], [3]] # 特征
y = [0, 0, 1, 1] # 标签# 实例化 KNN 分类器
estimator = KNeighborsClassifier(n_neighbors=2)# 使用 fit 方法进行训练
estimator.fit(x, y)# 数据预测
ret = estimator.predict([[10]]) # 输入一个新的特征
print(ret)

详细解释:
- 训练数据
x 是特征向量,y 是对应的标签:
x[0] = [0] 对应 y[0] = 0
x[1] = [1] 对应 y[1] = 0
x[2] = [2] 对应 y[2] = 1
x[3] = [3] 对应 y[3] = 1 - 使用训练数据进行拟合
estimator.fit(x, y) 训练模型后,它将 KNN 分类器的内部数据结构用训练数据(x 和 y)初始化,并准备进行预测。 - 当输入特征 [[10]] 进行预测时,KNN 会执行以下操作:
(1)计算距离:计算 10 与训练集中每个点的距离(使用欧几里得距离作为默认度量):
距离到 0 是 10 - 0 = 10
距离到 1 是 10 - 1 = 9
距离到 2 是 10 - 2 = 8
距离到 3 是 10 - 3 = 7
由于 10 远离了所有训练样本,因此它与所有训练样本间的距离都非常大。
(2)选择 K 个最近邻:因为设置了 n_neighbors=2,KNN 会选择最近的 2 个邻居。在这种情况下,它将选择距离和标签如下的最近的两个样本:
x[3] = [3], y[3] = 1(距离第三小)
x[2] = [2], y[2] = 1(距离第四小)
(3)投票决定输出:在仅考虑 2 个邻居的情况下,两个邻居的标签均为 1。因此,投票结果显示 1 是最多的,因此预测 ret 为 1。
3. 距离度量
3.1 距离公式
- 欧式距离:
- 二维空间距离:d12 = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt{( x_1-x_2)^2+( y_1-y_2)^2} (x1−x2)2+(y1−y2)2
- 三维空间距离:d12 = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 \sqrt{( x_1-x_2)^2+( y_1-y_2)^2+( z_1-z_2)^2} (x1−x2)2+(y1−y2)2+(z1−z2)2
- n维空间的距离:d12 = ∑ k = 1 n ( x 1 k − x 2 k ) 2 \sqrt{\sum\limits_{k = 1}^n( x_{1k}-x_{2k})^2} k=1∑n(x1k−x2k)2
- 曼哈顿距离:
- 二维平面上的两点距离:d12 = ∣ x 1 − x 2 ∣ \mid{ x_1-x_2}\mid ∣x1−x2∣ + ∣ y 1 − y 2 ∣ \mid{y_1-y_2}\mid ∣y1−y2∣
- n维空间的两点距离:d12 = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ \sum\limits_{k=1}^n\mid{ x_{1k}-x_{2k}}\mid k=1∑n∣x1k−x2k∣
- 切比雪夫距离:
- 二维平面上两点距离:d12 = max( ∣ x 1 − x 2 ∣ \mid{ x_1-x_2}\mid ∣x1−x2∣, ∣ y 1 − y 2 ∣ \mid{y_1-y_2}\mid ∣y1−y2∣)
- n维空间上两点距离:d12 = max( ∣ x 1 i − x 2 i ∣ \mid{ x_{1i}-x_{2i}}\mid ∣x1i−x2i∣)
- 闵可夫斯基距离:
- n维变量间的闵可夫斯基距离为:d12 = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ p p \sqrt[p]{\sum\limits_{k = 1}^n \mid{x_{1k}-x_{2k}}\mid^p} pk=1∑n∣x1k−x2k∣p
- 其中p是一个可变参数
- p=1,就是曼哈顿距离
- p=2,就是欧式距离
- p → ∞ \rightarrow\infty →∞,就是切比雪夫距离
3.2 其他距离公式
3.2.1 标准化欧式距离
- 针对欧式距离的改进
- 数据各维度分量分布不一样,先将各个分量标准化到均值,方差相等
- 标准化欧式距离公式:d12 = ∑ k = 1 n ( x 1 k − x 2 k S k ) 2 \sqrt{\sum\limits_{k = 1}^n(\frac{x_{1k}-x_{2k}}{S_k})^2} k=1∑n(Skx1k−x2k)2
- 如果将方差的倒数看成一个权重,也可称之为加权欧式距离
3.2.2 余弦距离
- 几何中,夹角余弦可以用来衡量两个方向上的差异,机器学习中,借用这一概念来衡量样本向量之间的差异
- 二维空间中向量A(x1, y1)与向量B(x2, y2)的夹角余弦公式: cos θ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 + x 2 2 + y 2 2 \cos\theta=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}+\sqrt{x_2^2+y_2^2}} cosθ=x12+y12+x22+y22x1x2+y1y2
- 两个n维样本点a(x11, x12,… ,x1n)和b(y21, y22,… ,y2n)的夹角余弦为: cos ( θ ) = a ⋅ b ∣ a ∣ ∣ b ∣ \cos(\theta)=\frac{a·b}{\mid{a}\mid\mid{b}\mid} cos(θ)=∣a∣∣b∣a⋅b
即: cos ( θ ) = ∑ k = 1 n x 1 k x 2 k ∑ k = 1 n x 1 k 2 ∑ k = 1 n x 2 k 2 \cos(\theta)=\frac{\sum\limits_{k=1}^n{x_{1k}x_{2k}}}{\sqrt{\sum\limits_{k=1}^n{x_{1k}^2}}\sqrt{\sum\limits_{k=1}^n{x_{2k}^2}}} cos(θ)=k=1∑nx1k2k=1∑nx2k2k=1∑nx1kx2k - 夹角的余弦范围为[-1, 1],余弦越大表示两个向量的夹角越小,余弦越小表示两个向量的夹角越大,当两个向量的方向重合时余弦取最大值1,当两个向量的方向完全相反余弦取最小值-1
3.2.3 汉明距离
两个等长字符串s1与s2的汉明距离为:将其中一个变换成另一个所需要做的最小字符替换次数
3.2.4 杰卡德距离
- 杰卡德相似系数:两个集合A和B的交集元素在A,B并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示: J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ J(A,B)=\frac{\mid{A\cap{B}}\mid}{\mid{A\cup{B}}\mid} J(A,B)=∣A∪B∣∣A∩B∣
- 杰卡德距离: J δ ( A , B ) = 1 − J ( A , B ) = ∣ A ∪ B ∣ − ∣ A ∩ B ∣ ∣ A ∪ B ∣ J_\delta(A,B)=1-J(A,B)=\frac{\mid{A\cup{B}}\mid-\mid{A\cap{B}}\mid}{\mid{A\cup{B}}\mid} Jδ(A,B)=1−J(A,B)=∣A∪B∣∣A∪B∣−∣A∩B∣
3.2.5 马氏距离
- 基于样本分布的一个距离,表示数据协方差距离,有效计算两个位置样本集的相似度方法
- 马氏距离定义: 设总体G为m维总体(考察m个指标),均值向量为 μ = ( μ 1 , μ 2 , . . . , μ m ) \mu=(\mu_1, \mu_2, ..., \mu_m) μ=(μ1,μ2,...,μm),协方差阵为: ∑ = ( σ i j ) \sum=(\sigma_{ij}) ∑=(σij)
则样本x = ( x 1 , x 2 , . . . , x m x_1, x_2,...,x_m x1,x2,...,xm)与总体G的马氏距离定义为: d 2 ( X , G ) = ( X − μ ) ′ ∑ − 1 ( X − μ ) d^2(X,G) = (X-\mu)^\prime\sum^{-1}(X-\mu) d2(X,G)=(X−μ)′∑−1(X−μ)
当m=1时, d 2 ( x , G ) = ( x − μ ) ′ ( x − μ ) σ 2 = ( x − μ ) 2 σ 2 d^2(x,G)=\frac{(x-\mu)^\prime(x-\mu)}{\sigma^2}=\frac{(x-\mu)^2}{\sigma^2} d2(x,G)=σ2(x−μ)′(x−μ)=σ2(x−μ)2
4. KNN算法中k值如何选择
4.1 K值影响
- K值过小:容易受到异常点影响
- K值过大:受样本均衡问题
4.2 两个概念
- 近似误差:
- 对现有训练集的训练误差,关注训练集
- 近似误差过小可能会出现过拟合情况,对现有训练集能有很好的预测,但是对未知测试样本将会出现比较大的偏差
- 模型本身不是接近最佳模型
- 估计误差:
- 对测试集的测试误差,关注测试集
- 估计误差小说明对未知数据预测能力好
- 模型本身是接近最佳模型
5. kd树
- 树的建立
- 最近邻域搜索:
kd树是一种对k维空间中的实例点进行存储以便对其快速检索的树形数据结构,kd树是一种二叉树,表示对k维空间的一个划分,构造kd树相当于不断的用垂直于坐标的超平面将k维空间切割构成一系列k维超矩形区域,kd树的每一个节点对应一个k维超矩形区域,利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量
5.1 构造方法
- 构造根节点,使根节点对应于K维空间包含所有实例节点的超矩形区域
- 通过递归的方法,不断的对k维空间进行划分,生成子节点
- 上述过程直到子区域没有实例为止(终止时的节点为叶节点)
- 循环的选择坐标对空间切分,选择训练实例点在坐标轴上中位数为切分点,这样得到的kd树是平衡的
6. scikit-learn数据集API的介绍
6.1 调用参数
- sklearn.datasets
- 加载获取流行的数据集
- datasets.load*()
- 获取小规模数据集,数据包含在datasets里
- datasets.fetch_*(data_home=None)
- 获取大规模数据集,需要从网络上下载,函数的第一个参数是data_home,表示数据下载的目录
6.2 sklearn数据集返回值
- 返回的是datasets.base.Bunch(字典格式)
- data: 特征数据数组,是[n_samples * n_features]的二维numpy.ndarray数组
- target: 标签数组,是n_samples的一维numpy.ndarray数组
- DESCR: 数据描述
- feature_names: 特征名,新闻数据,手写数字,回归数据集
- target_names: 标签名
from sklearn.datasets import load_irisiris = load_iris()# 特征值
# print(iris.data)
# 目标值
# print(iris.target)
# 特征值名字
print(iris.feature_names)
# 目标值名字
print(iris.target_names)
# 描述
# print(iris.DESCR)

6.3 数据可视化
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_irisiris = load_iris()
# 把数据转化成dataFrame格式
iris_d = pd.DataFrame(iris['data'], columns=['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])
iris_d['Species'] = iris.targetdef plot_iris(iris_d, col1, col2):sns.lmplot(x=col1, y=col2, data=iris_d, hue='Species', fit_reg=False)# 设置字体plt.rcParams['font.sans-serif'] = ['SimHei']plt.xlabel(col1)plt.ylabel(col2)plt.title('鸢尾花分布图')plt.savefig('./pic.png', dpi=100)plt.show()plot_iris(iris_d, 'Petal_Length', 'Sepal_Length')
6.4 数据集划分
sklearn.model_selection.train_test_split(arrays, *options)
- 参数
- x: 数据的特征值
- y: 数据的标签值
- test_size: 测试集的大小,一般为float
- random_state: 随机数种子,不同种子会造成不同的随机采样结果,相同种子采样结果相同
- return
- x_train x_test y_train y_test: 特征值的训练集、测试集,目标值的训练集、测试集
# -*- coding: utf-8 -*-
# @Time: 2024/11/3 20:13
# @File: 数据集的划分.py
# @Author: xujie.qu
# @Des:
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_splitiris = load_iris()
# 把数据转化成dataFrame格式
iris_d = pd.DataFrame(iris['data'], columns=['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])
iris_d['Species'] = iris.target
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
print("训练集的特征值是:\n",x_train)
print("训练集的目标值是:\n", y_train)
print("测试集的特征值是:\n",x_test)
print("测试集的目标值是:\n", y_test)
7. 特征值
7.1 特征预处理
7.1.1 定义
通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
7.1.2 原因
特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级,容易影响或支配目标结果,使得一些算法无法学习到其他特征
7.2 归一化和标准化
7.2.1 归一化
7.2.1.1 定义
通过对原始数据进行变化把数据映射到[0,1]之间
7.2.1.2 公式
X ′ = x − m i n m a x − m i n X^\prime=\frac{x-min}{max-min} X′=max−minx−min
X ′ ′ = X ′ ∗ ( m x − m i ) + m i X''=X'*(mx-mi)+mi X′′=X′∗(mx−mi)+mi
7.2.1.3 API
sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1)...)
- MinMaxScaler.fit_transform(X)
- X: numpy array格式化数据[n_namespaces, n_features]
- 返回值
- 转换后的形状相同的array
7.2.1.4 数据计算
from sklearn.preprocessing import MinMaxScaler
import pandas as pddef minmax_demo():data = pd.read_csv('dating.txt')print('归化前:\n',data)# 实例化一个转换器transfer = MinMaxScaler(feature_range=(0, 1))# 调用fit_transformdata = transfer.fit_transform(data[['milage','Liters','Consumtime']])print('处理结果:\n',data)return Noneminmax_demo()

7.2.1.5 缺点
最大值最小值是变化的,非常容易受到异常点的影响,鲁棒性较差,只适合传统精确小数据场景
7.2.2 标准化
7.2.2.1 定义
通过对原始数据进行变换把数据变换到均值为0,标准差为1的范围内
7.2.2.2 公式
X ′ = x − m e a n σ X'=\frac{x-mean}{\sigma} X′=σx−mean
7.2.2.3 API
sklearn.preprocessing.StandardScaler()
- 处理之后每列来说所有数据都聚集在均值0附近标准差差为1
- sklearn.preprocessing.StandardScaler.fit_transform(X)
- X: numpy array格式化数据[n_namespaces, n_features]
- 返回值
- 转换后的形状相同的array
7.2.2.4 数据计算
from sklearn.preprocessing import StandardScaler
import pandas as pddef stand_demo():data = pd.read_csv('dating.txt')# 实例化一个转换器类transfer = StandardScaler()# 调用fit_transformdata = transfer.fit_transform(data[['milage','Liters','Consumtime']])print('处理结果:\n', data)print('每一列特征值的平均值:\n', transfer.mean_)print('每一列特征值的方差:\n', transfer.var_)return Nonestand_demo()

8. 案例
- 鸢尾花案例
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
# 1. 获取数据
iris = load_iris()# 2. 数据基本处理
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)# 3. 特征工程 - 特征预处理
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)# 4. 机器学习KNN
# 1. 实例化一个估计器
estimator = KNeighborsClassifier(n_neighbors=5)# 使用估计器进行模型训练
estimator.fit(x_train, y_train)# 5. 模型评估
# 1. 预测值结果输出
y_pre = estimator.predict(x_test)
print("预测值是:\n", y_pre)
print("预测值和真实值对比:\n", y_pre == y_test)# 2. 准确率计算
score = estimator.score(x_test, y_test)
print("准确率是:\n", score)

9. 交叉验证&网格搜索
9.1 交叉验证定义
- 将拿到的训练数据,分为训练集和测试集,例:将数据分为4份,其中一份作为验证集,然后经过4次测试,每次都更换不同的验证集,即得到4组模型的结果,取平均值作为最终的结果
- 为了让被评估的模型更加准确可信
9.2 网格搜索定义
- 超参数:需要手动指定的参数(KNN中的K值)
- 手动过程繁杂,需要对模型预设几种超参数组合,每组超参数都采用交叉验证来进行评估,最后选出最优参数组合建立模型
9.3 模型选择与调优API
sklearn.model_selection.GridSearchCV(estimator, param_grid=None, cv=None)
- 对估计器的指定参数进行详尽搜索
- estimator: 估计器对象
- param_grid: 估计器参数(dict)
- cv: 指定几折交叉验证
- fit: 输入训练数据
- score: 准确率
- 结果分析
- bestscore_: 在交叉验证中验证的最好结果
- bestestimator: 最好的参数模型
- cvesults: 每次交叉验证后的验证集准确率结果和训练集准确率结果
相关文章:

【Python-AI篇】K近邻算法(KNN)
0. 前置----机器学习流程 获取数据集数据基本处理特征工程机器学习模型评估在线服务 1. KNN算法概念 如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中大多数属于某一个类别,则该样本也属于这一个类别 1.1 KNN算法流程总…...

aws xray如何实现应用log和trace的关联关系
参考资料 https://community.aws/tutorials/solving-problems-you-cant-see-using-aws-x-ray-and-cloudwatch-for-user-level-observability-in-your-serverless-microservices-applicationshttps://stackoverflow.com/questions/76000811/search-cloudwatch-logs-for-aws-xra…...

centos服务器登录失败次数设定
实现的效果 一台centos服务,如果被别人暴力或者登录次数超过多少次,就拒绝或者在规定时间内拒绝ip登录。这里使用的是fail2ban 安装fail2ban sudo yum install epel-release -y # 先安装 EPEL 源 sudo yum install fail2ban -y配置fail2ban # 复制默…...

实时高效,全面测评快递100API的物流查询功能
一、引言 你是否曾经在网购后焦急地等待包裹,频繁地手动刷新订单页面以获取最新的物流信息?或者作为一名开发者,正在为如何在自己的应用程序中高效地实现物流查询功能而发愁?其实,有一个非常好用的解决方案——快递10…...

第14张 GROUP BY 分组
一、分组功能介绍 使用group by关键字通过某个字段进行分组,对分完组的数据分别 “SELECT 聚合函数”查询结果。 1.1 语法 SELECT column, group_function(column) FROM table [WHERE condition] [GROUP BY group_by_expression] [ORDER BY column]; 明确&#…...
input子系统与相关框架)
笔记整理—linux驱动开发部分(10)input子系统与相关框架
关于输入类设备的系统有touch、按键、鼠标等,在系统中,命令行也是输入类系统。但是GUI的引入,不同输入类设备数量不断提升,带来麻烦,所以出现了struct input_event。 struct input_event {struct timeval time;//内核…...

[算法初阶]埃氏筛法与欧拉筛
素数的定义: 首先我们明白:素数的定义是只能整除1和本身(1不是素数)。 我们判断一个数n是不是素数时,可以采用试除法,即从i2开始,一直让n去%i,直到i*i<n c语言: #include<…...

【THM】linux取证 DisGruntled
目录 0x00 房间介绍 0x01 连接并简单排查 0x02 让我们看看做没做坏事 0x03 炸弹已埋下。但何时何地? 0x04 收尾 0x05 结论 0x00 房间介绍 嘿,孩子!太好了,你来了! 不知道您是否看过这则新闻,我…...
)
SpringBoot整合Freemarker(四)
escape, noescape 语法 <#escape identifier as expression>...<#noescape>...</#noescape>... </#escape> 用例 主要使用在相似的字符串变量输出,比如某一个模块的所有字符串输出都必须是html安全的,这个时候就可以使用&am…...

centos docker 安装 rabbitmq
安装docker 1.更新现有的软件包 首先,确保您的系统是最新的,可以通过运行以下命令来实现: sudo yum update -y 2.移除旧版本的Docker 如果您之前安装过Docker,可能需要先卸载旧版本。使用以下命令来卸载旧版本的Docker&#…...

手动实现promise的all,race,finally方法
Promise.all 是一个非常有用的工具,它接受一个 Promise 对象数组,并返回一个新的 Promise。当所有输入的 Promise 都成功解决时,新的 Promise 会解决为一个包含所有结果的数组;如果任何一个 Promise 被拒绝,新的 Prom…...

H5移动端预览PDF方法
新建页面 新建一个页面以便去预览对应的pdf 新建完后在 pages.json 文件内去新增对应路由 页面内容 <template><view class"page"><view class"pdf"><view id"demo"></view></view><view class"b…...

uniapp—android原生插件开发(1环境准备)
本篇文章从实战角度出发,将UniApp集成新大陆PDA设备RFID的全过程分为四部曲,涵盖环境搭建、插件开发、AAR打包、项目引入和功能调试。通过这份教程,轻松应对安卓原生插件开发与打包需求! 项目背景: UniApp集成新大陆P…...

《潜行者2切尔诺贝利之心》游戏引擎介绍
潜行者2切尔诺贝利之心是基于虚幻5引擎,所以画面效果大家不必担心。游戏目前已经跳票了很久,预计发售时间是2024 年 11 月 21 日,这次应该不会再跳票。 潜行者2切尔诺贝利之心是虚幻5吗 答:是虚幻5。 潜行者官方推特之前回复了…...

winform 加载 office excel 插入QRCode图片如何设定位置
需求:winform 加载 office excel 并加载QRCode图片,但是每台PC打印出来QRCode位置都不太一样,怎么办呢? 我的办法: 1、在sheet中插入一个 textbox ,改名 qrcode (这个名字随便设置)…...

简易入手《SOM神经网络》的本质与原理
原创文章,转载请说明来自《老饼讲解神经网络》:www.bbbdata.com 关于《老饼讲解神经网络》: 本网结构化讲解神经网络的知识,原理和代码。 重现matlab神经网络工具箱的算法,是学习神经网络的好助手。 目录 一、入门原理解说 01.…...

21.assert断言
assert(断言)主要用于在程序运行过程中检查某个条件是否满足,如果不满足则会触发错误并终止程序执行,可以帮助程序员在开发阶段及时发现可能存在的逻辑错误等问题。 通过断言调试程序,abotr() has been called 就是断言…...

15分钟学 Go 第 46 天 : 监控与日志
第46天:监控与日志 学习目标 了解如何实现应用监控与日志管理,掌握相关工具和最佳实践。 内容结构 引言监控的概念与工具 监控的定义常见监控工具 日志管理的概念与工具 日志的重要性常见日志管理工具 实现监控与日志的最佳实践 监控指标日志格式 实战…...

BFS 算法专题(四):多源 BFS
目录 1. 01 矩阵 1.1 算法原理 1.2 算法代码 2. 飞地的数量 2.1 算法原理 2.2 算法代码 3. 地图中的最高点 3.1 算法原理 3.2 算法代码 4. 地图分析 4.1 算法原理 4.2 算法代码 1. 01 矩阵 . - 力扣(LeetCode) 1.1 算法原理 采用 BFS 正难…...
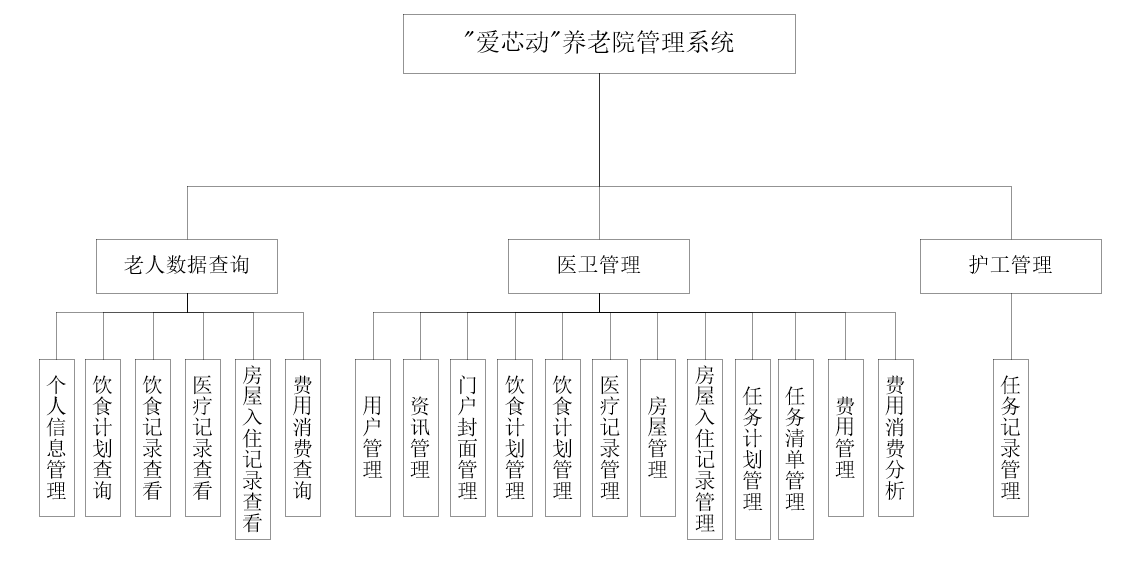
基于Spring Boot+Vue的养老院管理系统【原创】
一.系统开发工具与环境搭建 1.系统设计开发工具 后端使用Java编程语言的Spring boot框架 项目架构:B/S架构 运行环境:win10/win11、jdk17 前端: 技术:框架Vue.js;UI库:ElementUI; 开发工具&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

数据库优化实战指南:提升性能的黄金法则
在现代软件系统中,数据库性能直接影响应用的响应速度和用户体验。面对数据量激增、访问压力增大,数据库性能瓶颈经常成为项目痛点。如何科学有效地优化数据库,提升查询效率和系统稳定性,是每位开发与运维人员必备的技能。 本文结…...
