深入解析Python中的逻辑回归:从入门到精通
引言
在数据科学领域,逻辑回归(Logistic Regression)是一个非常重要的算法,它不仅用于二分类问题,还可以通过一些技巧扩展到多分类问题。逻辑回归因其简单、高效且易于解释的特点,在金融、医疗、广告等多个行业中得到广泛应用。本文将带你深入了解逻辑回归的基本原理、基础语法、实际应用以及一些高级技巧,无论你是初学者还是有经验的开发者,都能从中受益匪浅。
基础语法介绍
逻辑回归的核心概念
逻辑回归是一种用于解决分类问题的统计模型。与线性回归不同,逻辑回归的输出是一个概率值,表示某个样本属于某一类别的可能性。逻辑回归使用Sigmoid函数(也称为Logistic函数)将线性组合的结果映射到0到1之间,从而得到一个概率值。
Sigmoid函数的公式如下:
[ \sigma(z) = \frac{1}{1 + e^{-z}} ]
其中,( z ) 是线性组合的结果,即 ( z = w_0 + w_1x_1 + w_2x_2 + \cdots + w_nx_n ),( w_i ) 是权重,( x_i ) 是特征值。
基本语法规则
在Python中,我们通常使用scikit-learn库来实现逻辑回归。以下是一些基本的语法规则:
-
导入库:
from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score, confusion_matrix, classification_report -
数据准备:
X = ... # 特征矩阵 y = ... # 目标变量 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) -
模型训练:
model = LogisticRegression() model.fit(X_train, y_train) -
模型预测:
y_pred = model.predict(X_test) -
评估模型:
accuracy = accuracy_score(y_test, y_pred) cm = confusion_matrix(y_test, y_pred) report = classification_report(y_test, y_pred) print(f"Accuracy: {accuracy}") print(f"Confusion Matrix:\n{cm}") print(f"Classification Report:\n{report}")
基础实例
问题描述
假设我们有一个数据集,包含患者的年龄、性别、血压等信息,目标是预测患者是否患有糖尿病。我们将使用逻辑回归来解决这个问题。
代码示例
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report# 读取数据
data = pd.read_csv('diabetes.csv')
X = data.drop('Outcome', axis=1)
y = data['Outcome']# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 训练模型
model = LogisticRegression()
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)print(f"Accuracy: {accuracy}")
print(f"Confusion Matrix:\n{cm}")
print(f"Classification Report:\n{report}")
进阶实例
问题描述
在现实世界中,数据往往存在不平衡问题,即某一类别的样本数量远多于其他类别。这种情况下,直接使用逻辑回归可能会导致模型偏向多数类。我们将探讨如何处理不平衡数据,并提高模型的性能。
高级代码实例
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from imblearn.over_sampling import SMOTE# 读取数据
data = pd.read_csv('imbalanced_data.csv')
X = data.drop('Target', axis=1)
y = data['Target']# 处理不平衡数据
smote = SMOTE(random_state=42)
X_resampled, y_resampled = smote.fit_resample(X, y)# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X_resampled, y_resampled, test_size=0.2, random_state=42)# 训练模型
model = LogisticRegression(class_weight='balanced')
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)print(f"Accuracy: {accuracy}")
print(f"Confusion Matrix:\n{cm}")
print(f"Classification Report:\n{report}")
实战案例
问题描述
在金融行业中,信用评分是一个重要的任务,银行需要根据客户的个人信息来决定是否批准贷款。我们将使用逻辑回归来构建一个信用评分模型,帮助银行更好地评估客户的风险。
解决方案
- 数据收集:收集客户的个人信息,包括年龄、收入、职业、信用历史等。
- 数据预处理:处理缺失值、异常值,进行特征工程。
- 模型训练:使用逻辑回归模型进行训练。
- 模型评估:评估模型的性能,调整参数以优化模型。
- 模型部署:将模型部署到生产环境中,实时预测客户的信用评分。
代码实现
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.preprocessing import StandardScaler# 读取数据
data = pd.read_csv('credit_score_data.csv')
X = data.drop('CreditScore', axis=1)
y = data['CreditScore']# 数据预处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)# 训练模型
model = LogisticRegression()
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)print(f"Accuracy: {accuracy}")
print(f"Confusion Matrix:\n{cm}")
print(f"Classification Report:\n{report}")
扩展讨论
正则化
逻辑回归中常用的正则化方法有L1正则化(Lasso)和L2正则化(Ridge)。正则化可以帮助防止过拟合,提高模型的泛化能力。在scikit-learn中,可以通过设置penalty参数来选择正则化方法。
model = LogisticRegression(penalty='l1', solver='liblinear')
多分类问题
逻辑回归不仅可以用于二分类问题,还可以通过“一对多”(One-vs-Rest, OvR)或“一对一”(One-vs-One, OvO)的方法扩展到多分类问题。scikit-learn默认使用OvR方法。
model = LogisticRegression(multi_class='ovr')
特征选择
在实际应用中,特征选择是非常重要的一步。可以通过递归特征消除(Recursive Feature Elimination, RFE)等方法来选择最重要的特征,从而提高模型的性能。
from sklearn.feature_selection import RFEmodel = LogisticRegression()
selector = RFE(model, n_features_to_select=5)
selector.fit(X, y)
selected_features = X.columns[selector.support_]
print(f"Selected Features: {selected_features}")
模型解释
逻辑回归的一个优点是其可解释性强。通过查看模型的系数,可以了解每个特征对预测结果的影响。这对于业务决策非常重要。
coefficients = model.coef_[0]
feature_names = X.columns
for feature, coef in zip(feature_names, coefficients):print(f"{feature}: {coef}")
总结
逻辑回归作为一种经典的机器学习算法,在分类问题中表现出色。本文从基础语法到实际应用,再到高级技巧,全面介绍了逻辑回归的相关知识。希望本文能帮助你更好地理解和应用逻辑回归,无论是解决简单的二分类问题,还是复杂的多分类问题,都能游刃有余。
相关文章:

深入解析Python中的逻辑回归:从入门到精通
引言 在数据科学领域,逻辑回归(Logistic Regression)是一个非常重要的算法,它不仅用于二分类问题,还可以通过一些技巧扩展到多分类问题。逻辑回归因其简单、高效且易于解释的特点,在金融、医疗、广告等多个…...

【数据库】mysql数据库迁移前应如何备份数据?
MySQL 数据库的备份是确保数据安全的重要措施之一。在进行数据库迁移之前,备份现有数据可以防止数据丢失或损坏。以下是一套详细的 MySQL 数据库备份步骤,适用于大多数情况。请注意,具体的命令和工具可能因 MySQL 版本的不同而有所差异。整个…...

C语言——鸡兔同笼问题
没注释的源代码 #include <stdio.h> #include <stdlib.h> /* run this program using the console pauser or add your own getch, system("pause") or input loop */ int main(int argc, char *argv[]) { int tou 10; i…...

数据结构王道P234第二题
#include<iostream> using namespace std; int visit[MAxsize]; int color[MaxSize];//1表示红,2表示白; bool dfs(Graph G, int i){visit[i]1;ArcNode *p;bool flag1;for(pG.vertices[i].firsrarc; p ; pp->next){int jp->adjvex;if(!visi…...

层归一化和批归一化
层归一化是针对某一样本的所有特征,批归一化是针对所有样本的某一特征。 计算公式:(当前值 - 均值)/ 标准差。 作用:缓解梯度消失和梯度爆炸的问题,并提高网络的泛化性能。 为什么Transform和BERT中使用层归…...
Spring Cloud Gateway 网关
微服务网关 Spring Cloud Gateway https://docs.spring.io/spring-cloud-gateway/docs/current/reference/html/#gateway-request-predicates-factories Spring Cloud 在版本 2020.0.0 开始,去除了 Zuul 网关的使用,改用 Spring Cloud Gateway 作为网关…...

LabVIEW中的UDP与TCP比较
在LabVIEW中,UDP和TCP可以用于不同的网络通信场景,开发者可以根据需求选择合适的协议。以下是结合LabVIEW开发时的一些比较和应用场景: 1.TCP在LabVIEW中的应用: 可靠性高的场景:当开发一个对数据传输的准确性和完整…...

半导体器件与物理篇3 P-N结
热平衡时的PN结 pn结的定义:由p型半导体和n型半导体接触形成的结 pn结的特性和关键变量包括:整流性(即电流单向导通的特性)、平衡费米能级(费米能级 E F E_F EF为常数, d E F d x 0 )、内建电势 \frac…...

深入剖析String类的底层实现原理
嘿嘿,家人们,今天咱们来模拟实现string,好啦,废话不多讲,开干! 1:string.h 1.1:构造函数与拷贝构造函数 1.1.1:写法一 1.1.2:写法二(给缺省值) 1.2:赋值运算符重载与operatror[]获取元素 1.3:容量与迭代器 1.4:reserve与resize 1.5:清空与判断是否为空 1.6:push_back与…...

#其它:面试题
第一面试官提问如下: 1、自我介绍 2、根据项目提问:混合开发调取api的通讯方式 3、技术提问:如何隐藏div,但是div需要存在 使用 visibility 隐藏: 1.visibility: hidden2.display: none 3.opcity: 04、css塌陷问题…...

计算机视觉中的双边滤波:经典案例与Python代码解析
🌟 计算机视觉中的双边滤波:经典案例与Python代码解析 🚀 Hey小伙伴们!今天我们要聊的是计算机视觉中的一个重要技术——双边滤波。双边滤波是一种非线性滤波方法,主要用于图像去噪和平滑,同时保留图像的边…...

【AI日记】24.11.17 看 GraphRAG 论文,了解月之暗面
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】 核心工作 内容:看 GraphRAG 论文时间:4 小时评估:不错,继续 非核心工作 内容:了解国内大模型方向,重点了解了创业独角兽-月之暗面&…...
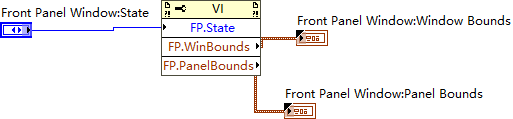
Front Panel Window Bounds 与 Front Panel Window Bounds 的区别与应用
在LabVIEW中,Front Panel Window Bounds 和 Front Panel WindowBounds 是两个不同的属性节点,用于描述前面板窗口的位置和大小。它们的区别主要体现在它们表示的是窗口的不同部分,具体如下: 1 Window Bounds:调整整个…...

比较TCP/IP和OSI/RM的区别
一、结构不同 1、OSI:OSI划分为7层结构:物理层、数据链路层、网络层、传输层、会话层、表示层和应用层。 2、TCP/IP:TCP/IP划分为4层结构:应用层、传输层、互联网络层和主机-网络层。 二、性质不同 1、OSI:OSI是制定…...

【Java项目】基于SpringBoot的【招聘信息管理系统】
技术简介:系统软件架构选择B/S模式、SpringBoot框架、java技术和MySQL数据库等,总体功能模块运用自顶向下的分层思想。 系统简介:招聘信息管理系统的功能分为管理员,用户和企业三个部分,系统的主要功能包括首页、个人中…...

【论文笔记】LLaMA-VID: An Image is Worth 2 Tokens in Large Language Models
🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。 基本信息 标题: LLaMA-VID: An Image is W…...
使用Web Storage API实现客户端数据持久化
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 使用Web Storage API实现客户端数据持久化 使用Web Storage API实现客户端数据持久化 使用Web Storage API实现客户端数据持久化…...

基于STM32F103的秒表设计-液晶显示
基于STM32F103的秒表设计-液晶显示 仿真软件: Proteus 8.17 编程软件: Keil 5 仿真实现: 在液晶1602上进行秒表显示,每100ms改变一次数值,一共三个按键,分为启动按键、暂停按键、复位按键。 电路介绍: 前面章节里已经和大家介绍了使用数码管设计的秒表,本次仿真将数…...

ReentrantLock的具体实现细节是什么
在 JDK 1.5 之前共享对象的协调机制只有 synchronized 和 volatile,在 JDK 1.5 中增加了新的机制 ReentrantLock,该机制的诞生并不是为了替代 synchronized,而是在 synchronized 不适用的情况下,提供一种可以选择的高级功能。 在 Java 中每个对象都隐式包含一个 monitor(监…...

【JavaScript】this 指向
1、this 指向谁 多数情况下,this 指向调用它所在方法的那个对象。即谁调的函数,this 就归谁。 当调用方法没有明确对象时,this 就指向全局对象。在浏览器中,指向 window;在 Node 中,指向 Global。&#x…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
