【算法】【优选算法】前缀和(下)
目录
- 一、560.和为K的⼦数组
- 1.1 前缀和
- 1.2 暴力枚举
- 二、974.和可被K整除的⼦数组
- 2.1 前缀和
- 2.2 暴力枚举
- 三、525.连续数组
- 3.1 前缀和
- 3.2 暴力枚举
- 四、1314.矩阵区域和
- 4.1 前缀和
- 4.2 暴力枚举

一、560.和为K的⼦数组
题目链接:560.和为K的⼦数组
题目描述:

题目解析:
- 求数组中子串的和为k的个数。
1.1 前缀和
解题思路:
- 假设已经创建好了一个前缀和数组dp,我们使用前缀和的时候,判断从0到 i 位置的和为k的子数组个数,只需要在dp下标[ 0 , i - 1 ]中找dp元素值为dp[ i ] - k的个数即可。
- 所以我们使用一个容器hash表来存储从0 到 i - 1的前缀和的个数,关键字key就是前缀和,values就是次数。
- 细节处理:
-
- 我们不需要真的使用前缀和数组,只需要遍历原数组时,用一个变量记录遍历过的元素和即可。
-
- 当该前缀和就是k的时候,我们上面条件没有考虑,所以我们还要先放入(0,1)表示这种情况。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {public int subarraySum(int[] nums, int k) {Map<Integer,Integer> hash = new HashMap<>();hash.put(0,1);int sum = 0;int ret = 0;for(int i = 0; i < nums.length; i++) {sum += nums[i];ret += hash.getOrDefault(sum-k,0);hash.put(sum, hash.getOrDefault(sum,0)+1);}return ret;}
}
1.2 暴力枚举
解题思路:
- 直接使用两层for循环,将每一种可能枚举出来。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {public int subarraySum(int[] nums, int k) {int ret = 0;for(int i = 0; i < nums.length; i++) {int sum = 0;for(int j = i; j < nums.length; j++) {sum += nums[j];if(sum == k) {ret++;}}}return ret;}
}
二、974.和可被K整除的⼦数组
题目链接:974.和可被K整除的⼦数组
题目描述:

题目解析:
- 跟上一道题一样的思路,只不过这个是求能被整除的个数而已。
2.1 前缀和
解题思路:
- 同余定理:如果(a - b)% p == 0 那么a % p 和b % p值相等。
- Java中负数对正数取余修正:在Java中负数对正数取余余数会是负数,修正方法就是:(a % p + p)% p
- 使用hash表将i下标前的每一个前缀和与k的余数存入。
- 再看前面前缀和与当前 前缀和的余数相同的个数即可。
- 当[0 , i]本身前缀和余数为0的时候,就是一个符合条件的子数组。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {public int subarraysDivByK(int[] nums, int k) {int ret = 0;Map<Integer,Integer> hash = new HashMap<>();hash.put(0 % k , 1);int sum = 0;for(int x : nums) {sum += x;int key = (sum % k + k ) % k;ret += hash.getOrDefault(key,0);hash.put(key, hash.getOrDefault(key , 0) + 1);}return ret;}
}
2.2 暴力枚举
解题思路:
- 直接遍历数组,在将遍历元素的和取余即可。
- 会超时。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {public int subarraysDivByK(int[] nums, int k) {int ret = 0;for(int i = 0; i < nums.length; i++) {int sum = 0;for(int j = i; j < nums.length; j++) {sum += nums[j];if((sum % k + k) % k == 0) ret++;}}return ret;}
}
三、525.连续数组
题目链接:525.连续数组
题目描述:

题目解析:
- 要我们返回子数组中 0 和1 数量相等的最长子数组的长度。
3.1 前缀和
解题思路:
- 我们使用一个容器hash表,关键字key来记录原数组每个下标i中的1与0个数差,而values记录这个差值的最小下标。
- 注意边界情况,如果刚好整个数组满足条件,结果就是数组长 又等于nums.length-1 + 1所以我们初始一个(0,-1)
- 求长度的时候,我们在前面找到 j 下标与现在 i 下标关键字一样,那么数组区间就是[ j+1 , i ]
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {public int findMaxLength(int[] nums) {int ret = 0;int n = nums.length;Map<Integer,Integer> hash = new HashMap<>();hash.put(0,-1);//前面1和0个数之差int num = 0;for(int i = 0; i < n; i++) {if(nums[i] == 0) num--;else num++;if(hash.containsKey(num)) ret = Math.max(ret, i - hash.get(num));else hash.put(num, i);}return ret;}
}
3.2 暴力枚举
解题思路:
- 两层for循环遍历数组,记录每一个子数组中1和0的个数,
- 当个数相同的时候,更新结果。
- 会超时
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {public int findMaxLength(int[] nums) {int ret = 0;for(int i = 0; i < nums.length; i++) {int oneNum = 0;int zeroNum = 0;for(int j = i; j < nums.length; j++) {if(nums[j] == 0) zeroNum++;else oneNum++;if(oneNum == zeroNum) ret = Math.max(ret,j-i+1);}}return ret;}
}
四、1314.矩阵区域和
题目链接:1314.矩阵区域和
题目描述:

题目解析:
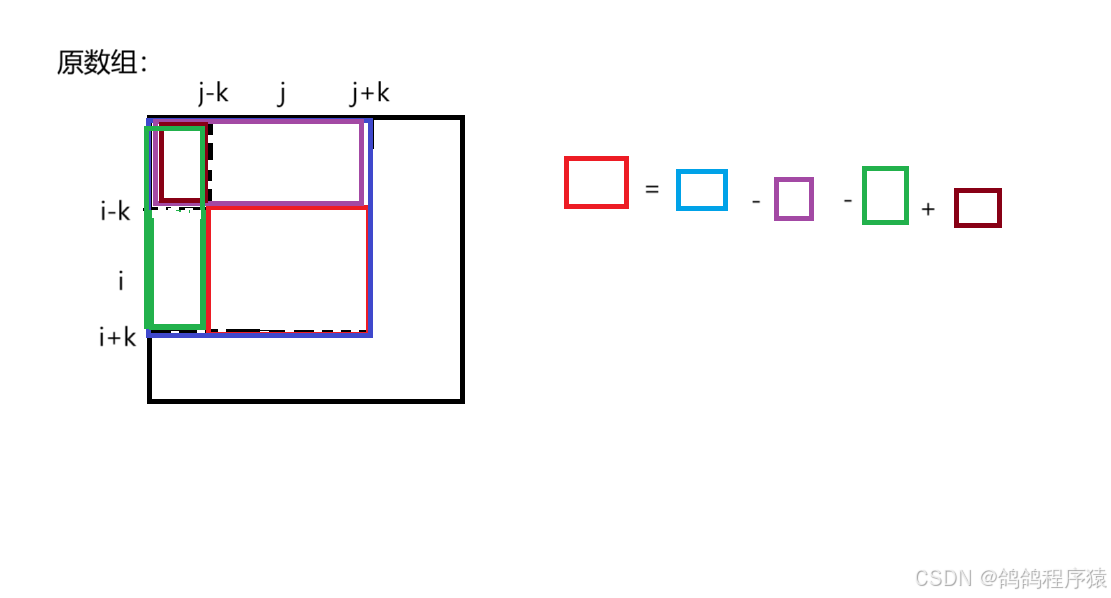
- 给一个二维数组,给一个k,返回的二维结果数组中数组( i , j )下标的值是原数组( i-k , j-k )到( i+k , j+k)的和。
- 就像下图中红方框框起来的:

4.1 前缀和
解题思路:
- 其实着就是前缀和上篇中给出的二维前缀和模版。
- 我们使用一个二维数组dp比原来数组多一行一列,dp[ i ][ j ]就是原数组中(0 , 0)到(i - 1 , j -1)的元素和。
- dp[ i ][ j ] = dp[ i - 1][j - 1] + nums[ i - 1][j - 1]。
- 在结果数组中与原数组大小一样,本来是求原数组( i-k , j-k )到( i+k , j+k)的和。那么对应到dp数组中,都要加1。
- 注意越界,如果( i-k , j-k )小于0那么就是0,i+k大于原数组行数,那么就是原数组行数,j+k大于原数组列数,那么就是原数组列数。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(n^2)
class Solution {public int[][] matrixBlockSum(int[][] mat, int k) {int n = mat.length;int m = mat[0].length;int[][] dp = new int[n+1][m+1];dp[0][0] = mat[0][0];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];} } int[][] ret = new int[n][m]; for(int i = 0; i < n; i++) {for(int j = 0; j < m; j++) {int x2 = i+k > n-1 ? n-1 : i+k;int y2 = j+k > m-1 ? m-1 : j+k;int x1 = i-k < 0 ? 0 : i-k;int y1 = j-k < 0 ? 0 : j-k;ret[i][j] = dp[x2+1][y2+1] - dp[x2+1][y1-1+1] - dp[x1-1+1][y2+1]+dp[x1-1+1][y1-1+1];}}return ret;}
}
4.2 暴力枚举
解题思路:
- 先两层for循环,拿到结果数组行列,
- 再两层for循环,求原数组( i-k , j-k )到( i+k , j+k)的和。
解题代码:
//时间复杂度:O(n^4)
//空间复杂度:O(1)
class Solution {public int[][] matrixBlockSum(int[][] mat, int k) {int n = mat.length;int m = mat[0].length;int[][] ret = new int[n][m];for(int i = 0; i < n; i++) {for(int j = 0; j < m; j++) {int x2 = i+k > n-1 ? n-1 : i+k;int y2 = j+k > m-1 ? m-1 : j+k;int x1 = i-k < 0 ? 0 : i-k;int y1 = j-k < 0 ? 0 : j-k;for(int w = x1; w <= x2; w++) {for(int q = y1; q <= y2; q++) {ret[i][j] += mat[w][q];}}}}return ret;}
}
相关文章:

【算法】【优选算法】前缀和(下)
目录 一、560.和为K的⼦数组1.1 前缀和1.2 暴力枚举 二、974.和可被K整除的⼦数组2.1 前缀和2.2 暴力枚举 三、525.连续数组3.1 前缀和3.2 暴力枚举 四、1314.矩阵区域和4.1 前缀和4.2 暴力枚举 一、560.和为K的⼦数组 题目链接:560.和为K的⼦数组 题目描述&#x…...

Node.js 23 发布了!
Node.js 23 现已推出,带来了新功能、性能改进和更好的开发者体验。此次版本提升了兼容性和稳定性,提供了更多工具来构建高效的应用程序。 此外,Node.js 22 将在 10 月 29 日当周被提升为长期支持 (LTS) 版本,进入长期维护阶段&am…...

如何通过低代码逻辑编排实现业务流程自动化?
随着数字化转型的加速,企业对高效、灵活的业务流程自动化需求日益增加。传统开发模式下的定制化解决方案往往周期长、成本高且难以适应快速变化的需求。低代码平台以其直观、简便的操作界面和强大的功能逐渐成为企业实现业务流程自动化的理想选择。本文将探讨低代码…...

thinkphp6模板调用URL方法生成的链接异常
var uul params.url ;console.log(params.url);console.log("{:Url(UserLog/index)}");console.log("{:Url("uul")}"); 生成的链接地址 UserLog/index /jjg/index.php/Home/UserLog/index.html /jjg/index.php/Home/Index/UserLog/index.html…...

Spring Boot汽车资讯:科技驱动的未来
4系统概要设计 4.1概述 本系统采用B/S结构(Browser/Server,浏览器/服务器结构)和基于Web服务两种模式,是一个适用于Internet环境下的模型结构。只要用户能连上Internet,便可以在任何时间、任何地点使用。系统工作原理图如图4-1所示: 4系统概要设计 4.1概…...

嵌入式硬件电子电路设计(五)LDO低压差线性稳压器全面详解
引言: LDO(Low Dropout Regulator,低压差线性稳压器)是一种常用的电源管理组件,用于提供稳定的输出电压,同时允许较小的输入电压与输出电压之间的差值。LDO广泛应用于各种电子设备中,特别是在对…...

qiankun主应用(vue2+element-ui)子应用(vue3+element-plus)不同版本element框架css样式相互影响的问题
背景:qiankun微前端架构实现多应用集成 主应用框架:vue2 & element-ui 子应用框架:vue3 & element-plus >> 问题现象和分析 登录页面是主应用的,在登录之后才能打开子应用的菜单页面,即加载子应用。 首…...

resnet50,clip,Faiss+Flask简易图文搜索服务
一、实现 文件夹目录结构: templates -----upload.html faiss_app.py 前端代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widt…...

使用OkHttp进行HTTPS请求的Kotlin实现
OkHttp简介 OkHttp是一个高效的HTTP客户端,它支持同步和异步请求,自动处理重试和失败,支持HTTPS,并且可以轻松地与Kotlin协程集成。OkHttp的设计目标是提供最简洁的API,同时保持高性能和低延迟。 为什么选择OkHttp …...
使用Mac下载MySQL修改密码
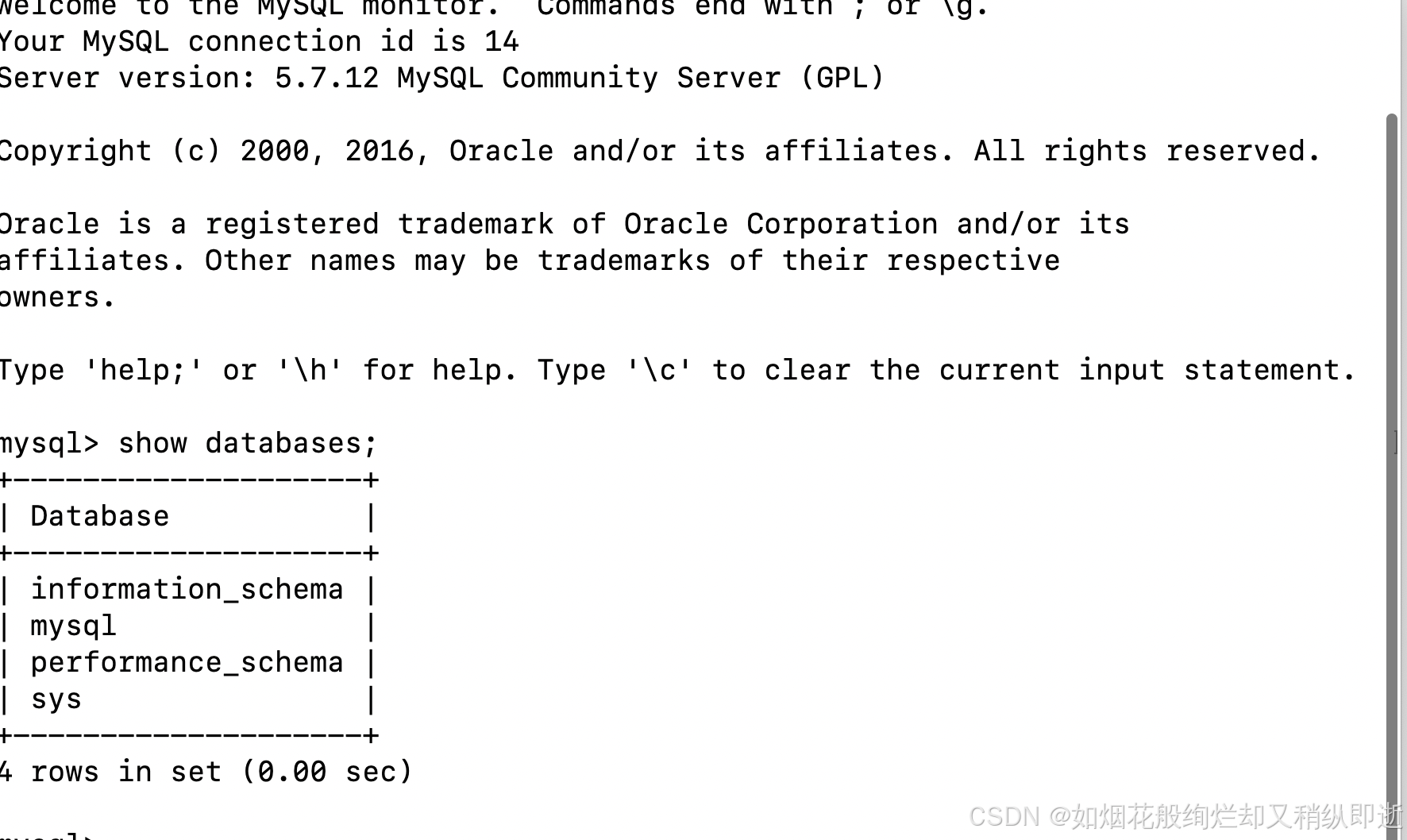
Mac下载MySQL MySQL官网链接MySQL 当进入到官网后下滑到community社区,进行下载 然后选择community sever下载 这里就是要下载的界面,如果需要下载之前版本的话可以点击archives, 可能会因为这是外网原因,有时候下…...

运维面试题.云计算面试题集锦第一套
运维+网络安全学科基础升就业 测试题(总分100分) 一,单词翻译(10分,直接写在答题卡上) 二,单选题(每题2分,共30题): 1.如下哪个属于管道符?( ) A、|| B、<< C、// D、| 2.有一备份程序mybackup,需要在周一至周五下午1点和晚上8点各运行一次,下面哪条cront…...

CSS-flex布局
flex常用语法 display: flex 父级元素相关 flex-direction 主轴方向【水平方向(默认)、垂直方向】justify-content 主轴上的对齐方式【flex-end结束对齐、space-between两端对齐、center】align-items 交叉轴的对齐方式【center、flex-end】flex-wrap…...

Linux:进程的优先级 进程切换
文章目录 前言一、进程优先级1.1 基本概念1.2 查看系统进程1.3 PRI和NI1.4 调整优先级1.4.1 top命令1.4.2 nice命令1.4.3 renice命令 二、进程切换2.1 补充概念2.2 进程的运行和切换步骤(重要) 二、Linux2.6内核进程O(1)调度队列(重要&#x…...

web应用安全和信息泄露
使用springboot开发的应用可能存在各种使用不当导致的信息泄露和漏洞,在此记录 1:spring actuator导致的信息泄露 使用spring actuator你可以选择通过使用HTTP端点或使用JMX来管理和监控你的应用程序。 审计、健康和指标收集也可以自动应用于你的应用程…...

创建vue3项目步骤
脚手架创建项目: pnpm create vue Cd 项目名称安装依赖:Pnpm iPnpm Lint:修复所有文件风格 ,不然eslint语法警告报错要双引号Pnpm dev启动项目 拦截错误代码提交到git仓库:提交前做代码检查 pnpm dlx husky-in…...

尽量通俗易懂地概述.Net U nity跨语言/跨平台相关知识
本文参考来自唐老狮,Unity3D高级编程:主程手记,ai等途径 仅作学习笔记交流分享 目录 1. .Net是什么? 2. .Net框架的核心要点? 跨语言和跨平台 .Net x Unity跨平台发展史 Net Framework 2002 Unity跨平台之 Mono 2004 Unity跨平台之 IL2CPP 2015 二者区别 .NET Core …...

【AlphaFold3】开源本地的安装及使用
文章目录 安装安装DockerInstalling Docker on Host启用Rootless Docker 安装 GPU 支持安装 NVIDIA 驱动程序安装 NVIDIA 对 Docker 的支持 获取 AlphaFold 3 源代码获取基因数据库获取模型参数构建将运行 AlphaFold 3 的 Docker 容器 参考 AlphaFold3: https://github.com/goo…...
vue2/vue3中使用的富文本编辑器vue-quill
前言: 整理下常用的富文本编辑器工具。 vue3: 实现效果: 实现步骤: 1、安装插件, 编辑器核心插件 vueup/vue-quill yarn add pnpm i npm i cnpm i vueup/vue-quill vueup/vue-quill 2、安装选择性插件 &a…...

论文阅读《BEVFormer v2》
BEVFormer v2: Adapting Modern Image Backbones to Bird’s-Eye-View Recognition via Perspective Supervision 目录 摘要1 介绍2 相关工作2.1 BEV三维目标检测器 摘要 我们提出了一种具有透视监督的新型鸟瞰图(BEV)检测器,其收敛速度更快…...
自动化运维(k8s):一键获取指定命名空间镜像包脚本
前言:脚本写成并非一蹴而就,需要不断的调式和修改,这里也是改到了7版本才在 生产环境 中验证成功。 该命令 和 脚本适用于以下场景:在某些项目中,由于特定的安全或政策要求,不允许连接到你的镜像仓库。然而…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...
