Python教程:运算符重载
在Python中,运算符重载是通过定义特殊方法(也称为魔术方法)来实现的,这些特殊方法允许类的实例像内置类型那样使用运算符。
Python提供了一系列这样的特殊方法,用于重载各种运算符。
以下是一些常见的运算符重载特殊方法及其对应的运算符:
add(self, other):重载加法运算符 +
sub(self, other):重载减法运算符 -
mul(self, other):重载乘法运算符 *
truediv(self, other):重载真除法运算符 /(在Python 3中)
floordiv(self, other):重载整除法运算符 //
mod(self, other):重载取模运算符 %
pow(self, other[, modulo]):重载幂运算符 **
radd(self, other):重载右加法运算符(用于反向操作,例如当左侧操作数不是该类的实例时)
iadd(self, other):重载就地加法运算符(用于 +=)
eq(self, other):重载等于运算符 ==
ne(self, other):重载不等于运算符 !=
lt(self, other):重载小于运算符 <
le(self, other):重载小于等于运算符 <=
gt(self, other):重载大于运算符 >
ge(self, other):重载大于等于运算符 >=
以下是一个简单的Python示例,展示了如何重载加法运算符 + 和等于运算符 ==:
class Vector: def __init__(self, x, y): self.x = x self.y = y def __add__(self, other): if isinstance(other, Vector): return Vector(self.x + other.x, self.y + other.y) return NotImplemented def __eq__(self, other): if isinstance(other, Vector): return self.x == other.x and self.y == other.y return NotImplemented def __repr__(self): return f"Vector({self.x}, {self.y})" # 使用示例
v1 = Vector(2, 3)
v2 = Vector(4, 5)
v3 = v1 + v2 # 调用 __add__ 方法
print(v3) # 输出: Vector(6, 8) v4 = Vector(2, 3)
print(v1 == v4) # 输出: True
print(v1 == v2) # 输出: False
在这个例子中,Vector 类定义了两个特殊方法:add 和 eq。add 方法用于重载加法运算符,允许两个 Vector 实例相加。eq 方法用于重载等于运算符,允许比较两个 Vector 实例是否相等。
注意,当重载运算符时,如果操作数类型不匹配,通常应该返回 NotImplemented,这样Python可以尝试使用反向运算符(例如,如果 a + b 不匹配,则尝试 b.radd(a))。这是Python运算符重载的一个约定俗成的做法,有助于保持代码的灵活性和健壮性。
相关文章:

Python教程:运算符重载
在Python中,运算符重载是通过定义特殊方法(也称为魔术方法)来实现的,这些特殊方法允许类的实例像内置类型那样使用运算符。 Python提供了一系列这样的特殊方法,用于重载各种运算符。 以下是一些常见的运算符重载特殊…...
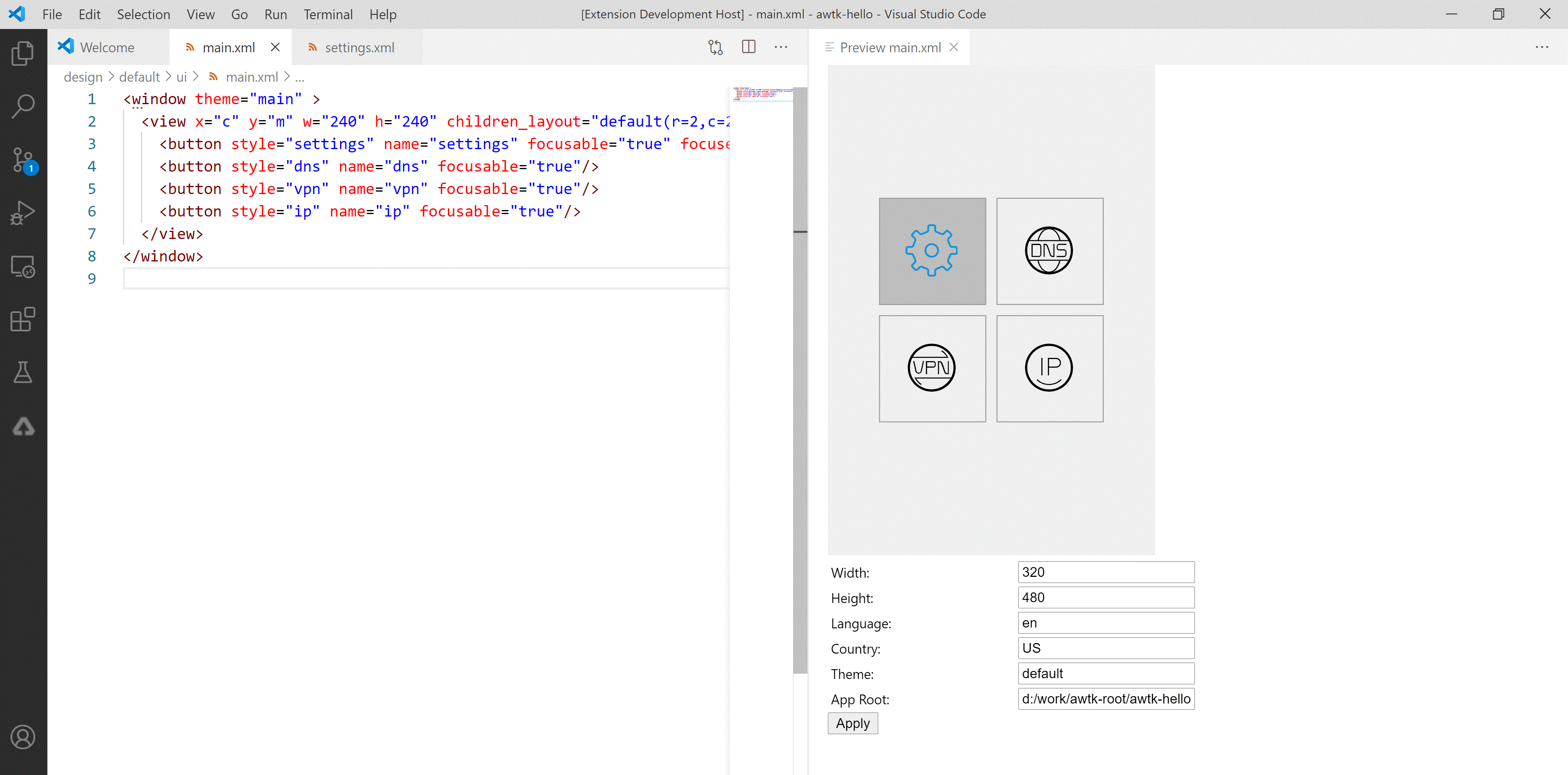
AWTK VSCode 实时预览插件端口冲突的解决办法
AWTK XML UI 预览插件:在 vscode 中实时预览 AWTK XML UI 文件,在 Copilot 的帮助下,可以大幅提高界面的开发效率。 主要特色: 真实的 UI 效果。可以设置主题,方便查看在不同主题下界面的效果。可以设置语言…...

【MySQL系列】深入理解MySQL中的存储、排序字符集
前言 在创建数据库时,我们经常会需要填写数据库的所用字符集、排序规则,字符集和排序规则是两个非常重要的概念,它们决定了数据库如何存储和比较字符串数据。在 MySQL 中,常用的存储字符集有 utf8、utf8mb4,而排序字符…...
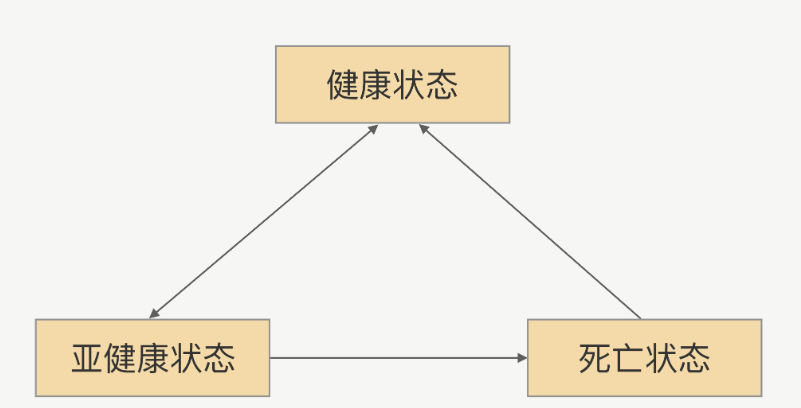
RPC-健康检测机制
什么是健康检测? 在真实环境中服务提供方是以一个集群的方式提供服务,这对于服务调用方来说,就是一个接口会有多个服务提供方同时提供服务,调用方在每次发起请求的时候都可以拿到一个可用的连接。 健康检测,能帮助从连…...
关于Java处理Excel常规列表记录,并入库的操作
1.描述 对于常规的Excel列表(二维表格)的入库处理,一般的mysql连接工具,例如Navicat就支持。但是,因为业务需要,不想每次都去手动导入,所以这里采用编码且定时任务的形式来实现。 2.Excel常规列…...

深入理解 JavaScript 中的 Array.find() 方法:原理、性能优势与实用案例详解
目录 深入理解 JavaScript 中的 Array.find() 方法:原理、性能优势与实用案例详解 一、引言:为什么要使用Array.find() 二、Array.find()的使用与技巧 1、基础语法 2、返回值 3、使用技巧 三、Array.find()的优势与实际应用案例 1、利用返回引用…...
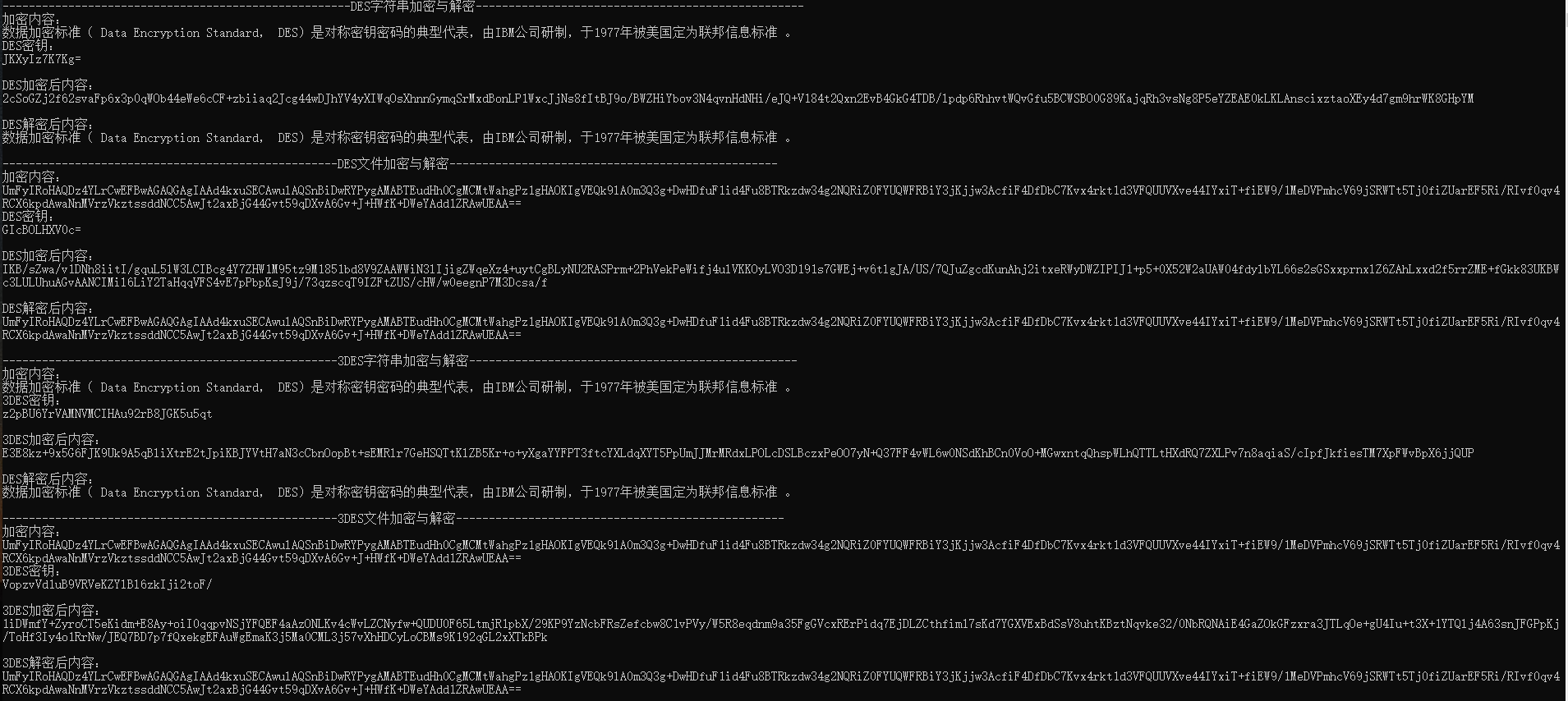
计算机网络安全 —— 对称加密算法 DES (一)
一、对称加密算法概念# 我们通过计算机网络传输数据时,如果无法防止他人窃听, 可以利用密码学技术将发送的数据变换成对任何不知道如何做逆变换的人都不可理解的形式, 从而保证了数据的机密性。这种变换被称为加密( encryptio…...
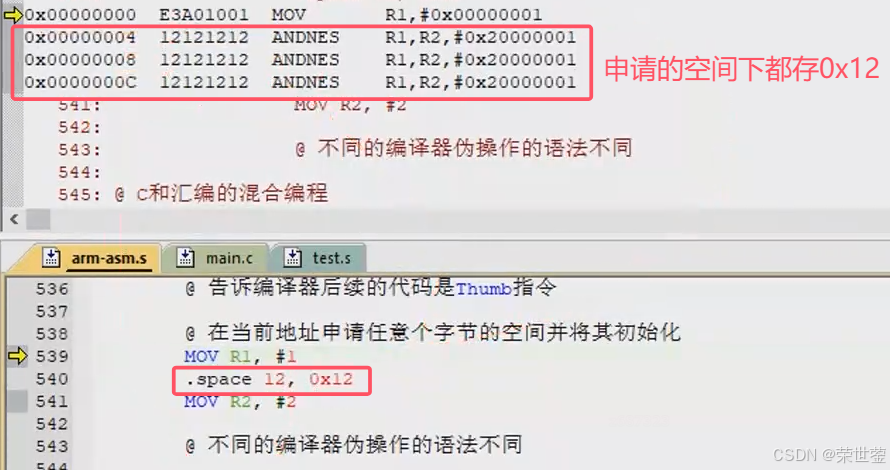
5. ARM_指令集
概述 分类 汇编中的符号: 指令:能够编译生成一条32位机器码,并且能被处理器识别和执行伪指令:本身不是指令,编译器可以将其替换成若干条指令伪操作:不会生成指令,只是在编译阶段告诉编译器怎…...

Jenkins的pipeline Script的 每个组件的详细讲解
在Jenkins的Pipeline脚本中,各个组件的配置和Groovy的一些常用函数起到了决定性的作用,帮助开发人员控制自动化流程的执行。以下是对Jenkins Pipeline的主要组件和Groovy常用函数的详细讲解: 1. Jenkins Pipeline主要组件 1.1 agent 功能&…...

Tomcat 和 Netty 的区别及应用场景分析
在 Java Web 开发中,Tomcat 和 Netty 都是常见的网络框架,它们各自有着不同的设计理念和适用场景。本文将通过详细的对比和实际场景示例,帮助你理解 Tomcat 和 Netty 在功能、性能、架构等方面的差异,帮助你在实际开发中做出更合理…...

6.C操作符详解,深入探索操作符与字符串处理
C操作符详解,深入探索操作符与字符串处理 C语言往期系列文章目录 往期回顾: C语言是什么?编程界的‘常青树’,它的辉煌你不可不知VS 2022 社区版C语言的安装教程,不要再卡在下载0B/s啦C语言入门:解锁基础…...

生数科技发布 Vidu 1.5 新版本,引领视频大模型新潮流
在国内视频大模型领域,生数科技一直以创新和突破而备受瞩目。近日,生数科技再度发力,发布了 Vidu 1.5 新版本,为视频创作带来了全新的变革与机遇。 Vidu 1.5 新版本在多个方面展现出了卓越的性能和创新的特点。首先,它…...

CentOS 7 aarch64停止更新后安装gcc8 —— 筑梦之路
CentOS 7.9非X86架构系统生命周期结束后(2024-6-30)配置在线可用yum源 —— 筑梦之路_centos7.9 arm-CSDN博客 以前的做法 sudo yum install centos-release-scl-rh sudo yum install devtoolset-8-buildsudo yum install devtoolset-8-gdb sudo yum i…...
WPF下 DataGrid加入序号列
先上代码: <DataGrid Name"DGV" AutoGenerateColumns"False" Grid.Row"0" Grid.Column"0" HorizontalGridLinesBrush"RoyalBlue" VerticalGridLinesBrush"Tomato" CanUserAddRows"False&qu…...

iOS UI 自动化 手势右滑退出当前页面
1、TouchAction from appium.webdriver.common.touch_action import TouchAction# 获取屏幕的宽度和高度 screen_width driver.get_window_size()["width"] screen_height driver.get_window_size()["height"]# 定义滑动的起点和终点坐标 start_x 0 en…...

《MySQL 实战教程:从零开始到高手进阶》
当然可以。下面是一篇关于MySQL的学习指南,它适合初学者到中级用户,涵盖了MySQL的基础知识、安装步骤、基本命令以及一些高级功能。 MySQL 学习指南 1. 了解 MySQL MySQL 是一个关系型数据库管理系统(RDBMS),由瑞典…...

第27天 安全开发-PHP应用TP 框架路由访问对象操作内置过滤绕过核心漏洞
时间轴 演示案例 TP 框架-开发-配置架构&路由&MVC 模型 TP 框架-安全-不安全写法&版本过滤绕过 TP 框架-开发-配置架构&路由&MVC 模型 参考: https://www.kancloud.cn/manual/thinkphp5_1 1、配置架构-导入使用 去thinkphp官网可以看到&…...

应用系统开发(12) Zync中实现数字相敏检波
在 Xilinx Zynq 系列(如 Zynq-7000 或 Zynq UltraScale+)中实现数字相敏检波(DSP,Digital Synchronous Detection)可以通过硬件(PL部分,FPGA逻辑)和软件(PS部分,ARM Cortex-A 处理器)的协同工作来实现。以下是一个详细的设计方法,包括基本原理和 Zynq 的实现步骤。…...

栈Stack和队列Queue
目录 一、栈 (1)用数组实现 (2)用单链表实现 (3)用标注尾结点的单链表实现 (4)用双向链表实现 2、栈的实际应用 (1)改变元素的序列 (2&am…...

uniapp 微信小程序地图标记点、聚合点/根据缩放重合点,根据缩放登记显示气泡marik标点
如图,如果要实现上方的效果: 上方两个效果根据经纬度标记点缩放后有重复点会添加数量 用到的文档地址https://developers.weixin.qq.com/miniprogram/dev/api/media/map/MapContext.addMarkers.htmlMapContext.addMarkers(Object object) 添加标记点Ma…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
