【机器学习】机器学习中用到的高等数学知识-1.线性代数 (Linear Algebra)
- 向量(Vector)和矩阵(Matrix):用于表示数据集(Dataset)和特征(Feature)。
- 矩阵运算:加法、乘法和逆矩阵(Inverse Matrix)等,用于计算模型参数。
- 特征值(Eigenvalues)和特征向量(Eigenvectors):用于降维(dimensionality reduction)(如主成分分析 PCA(Principal Component Analysis))和理解数据结构。
- 奇异值分解 (SVD):用于数据降维和矩阵近似。
向量和矩阵
向量
向量是线性代数中的一个基本概念,它是具有大小和方向的数学对象。向量在物理学、工程学、计算机科学和许多其他领域中都有广泛的应用。以下是向量的基本概念、性质和应用。
1. 向量的定义
向量可以用有序的数值集合来表示,通常写作 或
。在
-维空间中,一个向量可以表示为:
这里, 是向量的分量。
2. 向量的类型
向量可以根据其特征进行分类:
位置向量的用途
表示点的位置:可以用位置向量确定一个点在空间中的具体位置。
计算点间距离:两个点的距离可以通过它们的相对位置向量计算,例如 。
空间变换:位置向量可以用于描述平移、旋转等空间操作。
示例
若点 的坐标为
,则其位置向量为:
若点 在三维空间中的坐标为
,则其位置向量为:
位置向量的使用使得我们可以将几何问题转化为向量运算,使得计算更为简洁和直观。
- 零向量:是向量空间中的特殊向量,它的所有分量都为零。零向量通常用符号
表示,在任意维度的向量空间中都存在。例如:
在二维空间中,零向量为:
在
-维空间中,零向量为:
零向量的特点是无方向、无长度,它在向量加法中是单位元,添加到任何向量上都不会改变其值。 - 单位向量:模(长度)为 1 的向量,通常用于表示方向,单位向量的符号通常为
,
,
或加上帽子符号的其它向量符号。下面是一些常见的单位向量示例:
二维空间中的单位向量:
沿-轴方向的单位向量:
沿-轴方向的单位向量:
三维空间中的单位向量:
沿-轴方向的单位向量:
沿-轴方向的单位向量:
沿-轴方向的单位向量:
任意向量的单位化: 对于任意非零向量
,可以通过将它除以其模长
来获得单位向量:
例如,如果
,则它的模长为 5,单位向量为:
单位向量在多种计算中都很有用,尤其是表示方向,而不关注大小。
- 位置向量(Position Vector):表示空间中一个点的位置的向量,它通常从坐标系的原点
指向该点
,可以表示点的相对位置。位置向量是非常有用的工具,尤其在几何、物理学和工程中,用于描述物体的位置。
位置向量的定义
在二维和三维空间中,位置向量常以从原点到目标点的矢量形式表示。若点
二维空间中的位置向量: 若的坐标为
或
,则位置向量
为:
,则位置向量为:
三维空间中的位置向量: 若,则位置向量为:
3. 向量的运算
向量之间可以进行多种运算,包括:
-
向量加法:将两个相同维数的向量相加,对应分量相加。
-
向量减法:将两个相同维数的向量相减,对应分量相减。
-
数乘:将向量的每个分量乘以一个标量
。
4. 向量的性质
向量具有以下重要性质:
-
模(长度):向量的模可以通过以下公式计算:
-
点积(内积):两个向量的点积是一个标量,计算方式如下:
点积的结果可以用来判断两个向量的夹角关系,若
,则两者正交。
-
叉积(外积):仅在三维空间中定义,返回一个向量,计算方式为:
叉积的结果与两个向量均垂直,其大小等于两个向量夹角的正弦值乘以它们的模。
5. 向量的应用
向量在许多领域中有广泛的应用,包括:
- 物理学:描述力、速度、加速度等物理量。
- 工程学:在设计和分析中使用向量表示物体的位置和方向。
- 计算机图形学:用于表示图形、模型和运动。
- 机器学习:用于表示数据点和特征,进行分类和聚类。
6. 结论
向量是描述空间中大小和方向的基本工具,理解向量的性质和运算对于学习线性代数、物理学和工程学等领域至关重要。掌握向量的概念和应用能够为解决实际问题提供强有力的支持。
矩阵
矩阵是线性代数中的基本概念之一,它是一个按照矩形阵列排列的数值集合,通常用来表示线性方程组、线性变换、图像处理和其他许多数学和工程问题。以下是矩阵的基本概念、性质及应用。
1. 矩阵的定义
一个矩阵是由 行和
列的元素(通常是数字)组成的二维数组。矩阵通常用大写字母表示,例如
,其形式为:
这里, 是第
行第
列的元素。
2. 矩阵的类型
矩阵根据其特征可以分为几种类型:
- 行矩阵:只有一行的矩阵。
- 列矩阵:只有一列的矩阵。
- 方阵:行数与列数相同的矩阵(例如
矩阵)。
- 零矩阵:所有元素均为零的矩阵。
- 单位矩阵:对角线元素为 1,其他元素为 0 的方阵。
3. 矩阵的运算
矩阵之间可以进行多种运算,包括:
-
加法:两个相同维数的矩阵可以相加,对应元素相加。
-
减法:两个相同维数的矩阵可以相减,对应元素相减。
-
数乘:矩阵中的每个元素都可以乘以一个标量
。
-
矩阵乘法:两个矩阵相乘,只有当第一个矩阵的列数等于第二个矩阵的行数时才能进行。设
为
矩阵,
为
矩阵,结果矩阵
将是
矩阵。
4. 矩阵的性质
矩阵有许多重要的性质,包括:
-
转置矩阵:将矩阵的行和列互换,记作
。
-
迹:方阵的对角线元素之和,记作
。
-
行列式:方阵的一个标量值,反映了该矩阵的特性(如是否可逆),记作
或
。
-
逆矩阵:若矩阵
是可逆的,则存在一个矩阵
,使得
(单位矩阵)。
5. 矩阵的应用
矩阵在许多领域中有广泛的应用,包括:
- 线性方程组:可以用矩阵表示和求解线性方程组。
- 图形变换:在计算机图形学中,矩阵用于进行旋转、缩放和平移等变换。
- 数据分析:在机器学习和统计学中,矩阵用于表示数据集和执行各种运算。
- 网络分析:在图论中,邻接矩阵和权重矩阵用于表示网络结构。
6. 结论
矩阵是线性代数的核心工具,提供了一种有效的方式来表示和处理线性关系。掌握矩阵的基本概念、运算和性质对学习更高级的数学和应用至关重要。
矩阵运算
矩阵运算是线性代数的重要组成部分,广泛应用于计算机科学、物理学、统计学和机器学习等领域。主要的矩阵运算包括加法、减法、数乘、矩阵乘法、转置、求逆、以及行列式计算。以下是这些运算的简要概述和应用。
1. 矩阵加法和减法
-
加法:两个矩阵相加,需要它们的维度相同。对应元素相加形成新的矩阵。
例如,对于矩阵
和
,它们的和为:
-
减法:与加法类似,减法要求矩阵维度相同,对应元素相减。
2. 数乘(标量乘法)
一个矩阵的每个元素都与同一个标量(数值)相乘,称为数乘。若有矩阵 ,标量
,则:
3. 矩阵乘法
矩阵乘法需要左矩阵的列数等于右矩阵的行数,得到一个新的矩阵。假设 是
矩阵,
是
矩阵,则
为
矩阵,计算方式如下:
例如:
则
4. 矩阵转置
矩阵转置是将矩阵的行与列互换。对于 ,其转置
为:
5. 矩阵求逆
对于方阵 ,如果存在一个矩阵
使得
(单位矩阵),则
称为
的逆矩阵。矩阵求逆仅适用于方阵,且非所有方阵都有逆(只有行列式不为零的矩阵才有逆)。
6. 行列式
行列式是方阵的一个标量值,记为 ,可以用于判断矩阵是否可逆(行列式不为零时矩阵可逆)。例如,对于
,行列式
。
3x3 矩阵的行列式: 对于一个 的矩阵
,行列式为:
这就是通过展开法计算行列式。
Python 示例
使用 NumPy 库可以简便地实现这些矩阵运算:
import numpy as np# 创建矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
C = np.array([[2, 0], [1, 2]])# 矩阵加法
print("A + B =\n", A + B)# 矩阵减法
print("A - B =\n", A - B)# 数乘
print("3 * A =\n", 3 * A)# 矩阵乘法
print("A * C =\n", np.dot(A, C))# 矩阵转置
print("A^T =\n", A.T)# 矩阵求逆
try:A_inv = np.linalg.inv(A)print("A inverse =\n", A_inv)
except np.linalg.LinAlgError:print("A is not invertible")# 行列式
det_A = np.linalg.det(A)
print("det(A) =", det_A)
应用
矩阵运算在机器学习、数据科学、图像处理、物理模拟等领域极其重要,尤其在神经网络和线性回归等算法中被广泛应用。
特征值和特征向量
特征值和特征向量是线性代数中重要的概念,在许多科学与工程应用(例如数据降维、图像处理、推荐系统、自然语言处理等)中扮演关键角色。了解特征值和特征向量有助于理解数据中的模式,识别重要的方向和特征。
什么是特征值和特征向量?
假设有一个 方阵
,如果存在一个向量
和一个标量
,使得:
那么 就是矩阵
的特征向量,
就是对应的特征值。
解读:
- 特征向量:在矩阵作用下保持方向不变的向量。
- 特征值:是标量,表示在矩阵作用下特征向量的拉伸或缩放因子。
如何求特征值和特征向量?
-
特征值的求解:特征值的求解基于以下特征方程:
其中
是单位矩阵。通过解这个多项式方程,我们可以找到所有可能的特征值
。
-
特征向量的求解:在找到特征值
后,代入
并解线性方程组,可以找到对应的特征向量
。
示例
假设有矩阵 :
-
计算特征值:
展开行列式并解方程,得到特征值。
-
代入特征值解出特征向量。
矩阵的特征方程求解步骤如下:
步骤 1:定义矩阵和特征值
设有一个 的方阵
,其特征值定义为满足方程:
其中, 是特征向量,
是特征值。
步骤 2:构造特征方程
将方程 改写为:
这可以进一步表示为:
其中, 是单位矩阵,
是特征值。
为了有非零解 ,必须有:
这是特征方程。
步骤 3:展开行列式
计算 ,这是一个关于
的多项式。对于
的矩阵,展开行列式得到一个
次多项式:
其中, 是关于
的特征方程。这个多项式的根就是矩阵
的特征值。
步骤 4:求解特征值
解方程 ,得到特征值
。
举个例子
考虑一个 的矩阵:
构造特征方程:
求行列式:
解方程:
使用求根公式:
因此,特征值为:
这是矩阵 的特征值计算过程。
使用求根公式来解二次方程的过程是基于二次方程的标准形式和求解方法。二次方程的标准形式为:
其中,a、b、c 是常数,且 a ≠ 0。
求根公式的推导
二次方程的求根公式是通过配方或者使用判别式来得到的。具体步骤如下:
步骤 1:标准化二次方程
首先将二次方程写成标准形式:
然后,除以 (假设
):
步骤 2:完成平方式
接下来,我们需要通过配方来将方程转化为平方形式。首先,左边部分是一个完全平方式,因此我们将常数项移到右边:
然后在等式两边加上 :
这时左边已经是一个完全平方式:
简化右边:
步骤 3:解出 
对两边开平方:
最后,解出 :
这就是二次方程的求根公式:
特征值和特征向量的几何意义
特征向量指示矩阵变换作用下保持方向的“固有”方向,而特征值则表示这种“固有”方向的缩放程度。例如:
- 数据降维:在主成分分析(PCA)中,我们选择数据协方差矩阵的特征向量(即主成分)来保留主要信息。
- 图像压缩:在图像处理中的奇异值分解(SVD)中,我们可以通过保留矩阵的主要特征向量来减少数据维度。
Python 实现示例
以下代码使用 numpy 库来求矩阵的特征值和特征向量:
import numpy as np# 定义矩阵 A
A = np.array([[4, 1], [2, 3]])# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)
应用场景
- 主成分分析(PCA):用于数据降维和特征提取。
- 图像处理:特征值分解帮助从图像数据中提取信息。
- 稳定性分析:在物理学、工程学中,特征值可用于判断系统的稳定性(例如,控制系统的稳定性与特征值的正负相关)。
- 推荐系统:在矩阵分解中,特征值和特征向量帮助识别潜在的用户偏好模式。
特征值和特征向量提供了数据内在结构和变化方向的重要信息,因此在机器学习和数据分析中不可或缺。
奇异值分解 (SVD)
奇异值分解(Singular Value Decomposition, SVD)是一种在矩阵分解和数据分析中非常有用的工具,广泛应用于数据降维、噪声过滤、推荐系统、图像压缩等多个领域。
什么是奇异值分解?
对于任意一个 的矩阵
,可以将它分解为三个矩阵的乘积:
其中:
是一个
的正交矩阵,称为左奇异向量组成的矩阵。
是一个
的对角矩阵,称为奇异值矩阵,其中的元素为非负实数,且按照降序排列。这些非零的对角元素就是矩阵
的奇异值。
是一个
的正交矩阵,称为右奇异向量组成的矩阵。
奇异值分解的结构使得我们可以对矩阵 进行有效的压缩和分析。
假设我们有一个 矩阵:
步骤 1:计算  和
和 
为了计算 、
和
,首先需要计算
和
,它们分别的特征值和特征向量会帮助我们求出奇异值和奇异向量。
- 计算
:
然后计算:
- 计算
:
步骤 2:计算特征值和特征向量
-
计算
的特征值和特征向量:
的特征值即为矩阵
的奇异值的平方。
- 特征向量对应着右奇异向量。
-
计算
的特征值和特征向量:
的特征值也与矩阵
的奇异值相关。
- 特征向量对应着左奇异向量。
步骤 3:求解奇异值和奇异向量
假设计算出的特征值和特征向量为:
- 特征值(奇异值的平方):
- 7.7224 和 0.2776
- 奇异值(取平方根):
然后,得到右奇异向量 和左奇异向量
(通过对
和
的特征向量进行标准化得到)。
步骤 4:构造矩阵 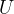 、
、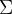 和
和 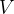
-
左奇异向量矩阵
:
的列由
的特征向量组成。假设计算出以下特征向量:
-
奇异值矩阵
:
-
右奇异向量矩阵
:
的列由
的特征向量组成。假设计算出以下特征向量:
步骤 5:重构矩阵 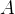
通过 ,我们可以验证分解的正确性,恢复原矩阵
。
总结
奇异值分解的关键步骤包括:
- 计算
和
。
- 求解它们的特征值和特征向量。
- 奇异值是特征值的平方根,右奇异向量来自
的特征向量,左奇异向量来自
的特征向量。
- 通过这些步骤,我们可以得到
、
和
矩阵,从而得到矩阵
的奇异值分解。
这个过程在实际应用中可以使用数值计算方法(如通过SVD算法的库函数)来计算。
SVD 的计算方法
- 计算矩阵的特征值和特征向量:我们可以通过
和
的特征值和特征向量来构造
和
矩阵。
- 构造奇异值矩阵:特征值的平方根便是奇异值,将这些奇异值排列在
矩阵的对角线上。
SVD 的几何意义
- 矩阵
的奇异值表示的是矩阵在不同方向上的拉伸或缩放程度。
- 奇异值较大的方向表示数据中的主要模式,而较小的奇异值方向则表示噪声或不重要的模式。因此,在数据降维中,我们可以保留最大的奇异值所对应的分量,从而获得矩阵的低秩近似。
SVD 的应用
- 数据降维:在主成分分析(PCA)中,我们可以使用 SVD 提取出数据的主成分,从而减少数据维度。
- 图像压缩:SVD 可以用于对图像进行压缩,通过保留最大的奇异值所对应的主成分来保持图像的大部分信息。
- 推荐系统:在协同过滤推荐系统中,SVD 用于用户和物品的隐式特征分解,可以帮助识别用户偏好。
- 噪声去除:通过丢弃小奇异值分量,我们可以从数据中去除噪声,提取出主要模式。
Python 示例
以下代码展示了如何使用 NumPy 进行奇异值分解:
import numpy as np# 定义矩阵 A
A = np.array([[3, 1, 1], [-1, 3, 1]])# 进行奇异值分解
U, S, Vt = np.linalg.svd(A)# SVD 分解结果
print("U 矩阵:\n", U)
print("奇异值(对角矩阵的对角元素):\n", S)
print("V 转置矩阵:\n", Vt)# 重构矩阵 A(通过 U * S * Vt)
S_matrix = np.zeros((U.shape[0], Vt.shape[0]))
np.fill_diagonal(S_matrix, S)
A_reconstructed = U @ S_matrix @ Vt
print("重构后的矩阵 A:\n", A_reconstructed)
应用示例:图像压缩
在图像压缩中,我们可以通过 SVD 提取最重要的奇异值分量来降低数据量。例如,若图像被表示为矩阵,SVD 分解后,保留最大的奇异值对应的前几列,可以保留图像的主要特征,同时去除冗余信息。
总结
奇异值分解提供了一种强大的方法来分析数据的主成分结构,有助于降维、数据压缩和模式识别。在实际应用中,SVD 尤其在高维数据处理中被广泛使用,比如文本数据、图像数据和推荐系统等。
相关文章:
【机器学习】机器学习中用到的高等数学知识-1.线性代数 (Linear Algebra)
向量(Vector)和矩阵(Matrix):用于表示数据集(Dataset)和特征(Feature)。矩阵运算:加法、乘法和逆矩阵(Inverse Matrix)等,用于计算模型参数。特征值(Eigenvalues)和特征向量(Eigenvectors)&…...

无插件H5播放器EasyPlayer.js网页web无插件播放器选择全屏时,视频区域并没有全屏问题的解决方案
EasyPlayer.js H5播放器,是一款能够同时支持HTTP、HTTP-FLV、HLS(m3u8)、WS、WEBRTC、FMP4视频直播与视频点播等多种协议,支持H.264、H.265、AAC、G711A、MP3等多种音视频编码格式,支持MSE、WASM、WebCodec等多种解码方…...

Idea中创建和联系MySQL等数据库
备注:电脑中要已下好自己需要的MySQL数据库软件 MySQL社区版下载链接: https://dev.mysql.com/downloads/installer/ 优点: 1.相比与在命令行中管理数据库,idea提供了图形化管理,简单明了; 2.便于与后端…...

【pytest】pytest注解使用指南
前言:在 pytest 测试框架中,注解(通常称为装饰器)用于为测试函数、类或方法提供额外的信息或元数据。这些装饰器可以影响测试的执行方式、报告方式以及测试的组织结构。pytest 提供了多种内置的装饰器,以及通过插件扩展…...
在Unity中使用Epplus写Excel
Overview 本文旨在帮助你快速入门,该库发展多年内容庞大(官方文档写的极好:https://github.com/EPPlusSoftware/EPPlus/wiki),有些功能在Unity环境可能你永远都不会使用. 官方的一个Demo: https://github.com/EPPlusSoftware/EPPlus.Samples.CSharp 如果你只有读的需求,可以…...

初识算法 · 模拟(2)
目录 前言: Z字形变换 题目解析 算法原理 算法编写 数青蛙 题目解析 算法原理 算法编写 前言: 本文的主题是模拟,通过两道题目讲解,一道是Z字形变化,一道是数青蛙。 链接分别为: 1419. 数青蛙…...
(详细))
【Java面试】—— 创建线程池的两种方式(执行流程、拒绝策略)(详细)
目录 一、ThreadPoolExecutor(推荐)(重点) 1、参数 2、执行流程 3、常用方法 4、任务拒绝策略 二、Executors(不推荐) 1、常用方法 2、存在的问题 一、ThreadPoolExecutor(推荐)(重点) 1、参数 使用指定的初始化参数创建一个新的线程池对象 public Thread…...

Docker在微服务架构中的应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 Docker在微服务架构中的应用 Docker在微服务架构中的应用 Docker在微服务架构中的应用 引言 Docker 基本概念 1. 容器 2. 镜像 3…...

苹果ASA归因对接以及API接入
一、归因概要 广告归因,目的是用于衡量广告带来的激活用户的成本以及后续进一步的用户质量表现。 Apple Ads 广告平台是基于 App Store(站内广告),同时属于自归因平台(通常称为 SAN)。这两个因素ÿ…...

Git常用操作学习
目录 Git基础概述 1.1 什么是Git? 1.2 Git的优点Git工作流程 2.1 集中式工作流程 2.2 功能分支工作流程 2.3 Git Flow工作流程克隆仓库 3.1 使用git clone 3.2 克隆特定分支分支管理 4.1 创建分支 4.2 切换分支 4.3 合并分支 4.4 删除分支提交和推送更改 5.1 查看状…...

2.5D视觉——Aruco码定位检测
目录 1.什么是Aruco标记2.Aruco码解码说明2.1 Original ArUco2.2 预设的二维码字典2.3 大小Aruco二维码叠加 3.函数说明3.1 cv::aruco::detectMarkers3.2 cv::solvePnP 4.代码注解4.1 Landmark图说明4.2 算法源码注解 1.什么是Aruco标记 ArUco标记最初由S.Garrido-Jurado等人在…...

【PSQLException: An I/O error occurred while sending to the backend.】
PSQLException: An I/O error occurred while sending to the backend. java项目定时任务执行耗时很长的sql语句(很多条sql,从很多表中,很多数据中查询,处理)总之,耗时很长(PG数据库)。报错I/O error,Caused by : java.net.SocketTimeoutException: Read time out场景…...

图像基础算法学习笔记
目录 概要 一、图像采集 二、图像标注 四、图像几何变换 五、图像边缘检测 Sobel算子 Scharrt算子 Laplacian算子 Canny边缘检测 六、形态学转换 概要 参考书籍:《机器视觉与人工智能应用开发技术》 廖建尚,钟君柳 出版时间:2024-…...

【Elasticsearch】01-ES安装
1. 安装 安装elasticsearch。 docker run -d \--name es \-e "ES_JAVA_OPTS-Xms512m -Xmx512m" \-e "discovery.typesingle-node" \-v es-data:/usr/share/elasticsearch/data \-v es-plugins:/usr/share/elasticsearch/plugins \--privileged \--networ…...

网络性能测试
一、iperf网络性能测试工具 测试udp丢包率 在服务器启动 iperf 服务端 iperf -p 9000 -s -u -i 1参数说明: -p : 端口号 -s : 表示服务端 -u : 表示 udp 协议 -i : 检测的时间间隔(单位,秒) 在客户端,启动 iperf 客户端 iperf -c xxx.xxx.14…...

docker:docker: Get https://registry-1.docker.io/v2/: net/http: request canceled
无数次的拉镜像让人崩溃: rootnode11:~/ragflow/docker# more rag.sh #export HTTP_PROXYhttp://192.168.207.127:7890 #export HTTPS_PROXYhttp://192.168.207.127:7890 #export NO_PROXYlocalhost,127.0.0.1,.aliyun.com docker compose -f docker-compose-gpu-C…...
esp32c3开发板通过micropython的mqtt库连MQTT物联网消息服务器
MQTT介绍 MQTT(Message Queuing Telemetry Transport)是一种轻量级的消息协议,旨在设备之间进行通信,尤其是在网络条件较差的情况下。MQTT v3.1.1 和 MQTT v5 是该协议的两个主要版本。 MQTT v3.1.1: 优点ÿ…...
OceanBase 升级过程研究(4.2.1.6-4.2.1.8)
模拟业务 使用benchmark加载10仓数据模拟业务场景 升级方法 使用滚动升级方式来进行OB升级。该方法前提是OB集群必须满足官方规定的高可用架构(如果 Zone 个数小于 3,滚动升级时则无法构成多数派), 滚动升级的原理就是轮流完成每个ZONE的升级工作,由于…...

ubuntu下怎么设置机器程序开机自启?
在 Ubuntu 中,可以通过多种方法设置程序或脚本在系统启动时自动运行。以下是几种常见方法: 方法 1:使用 crontab crontab 是一个定时任务管理工具,可以用来设置程序在开机时自动运行。 1. 打开终端,编辑当前用户的 …...

Cesium 相机系统
Cesium 的相机系统是其 3D 地球渲染引擎的重要组成部分,它控制用户在虚拟地球上的视图和交互体验。Cesium 的相机系统具备灵活性和强大的功能,允许开发者自定义视图、导航和交互方式。以下是 Cesium 相机系统的主要特点和功能: 1. 相机的基本…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
