机器学习(贝叶斯算法,决策树)
朴素贝叶斯分类
贝叶斯分类理论
假设现有两个数据集,分为两类

我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中红色圆点表示的类别)的概率,用p2(x,y)表示数据点(x,y)属于类别2(图中蓝色三角形表示的类别)的概率,那么对于一个新数据点(x,y),可以用下面的规则来判断它的类别:
-
如果p1(x,y)>p2(x,y),那么类别为1
-
如果p1(x,y)<p2(x,y),那么类别为2
条件概率
条件概率是指在一定条件下事件发生的概率

P(A|B)即表示事件B发生的情况下,事件A发生的概率。
有图可知:在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
𝑃(A|B)=𝑃(A∩B)/𝑃(B)
变换可得
𝑃(A∩B)=𝑃(A|B)𝑃(B) 或𝑃(A∩B)=𝑃(B|A)𝑃(A)
即:𝑃(𝐴|𝐵)=𝑃(B|A)𝑃(𝐴)/𝑃(𝐵)
这为条件概率公式。
全概率公式
假定样本空间S,是两个事件A与A'的和。

红色部分是事件A,绿色部分是事件A',它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。

事件B的概率即可表示为:𝑃(𝐵)=𝑃(𝐵∩𝐴)+𝑃(𝐵∩𝐴′)
由上可得:𝑃(𝐵∩𝐴)=𝑃(𝐵|𝐴)𝑃(𝐴)
所以:𝑃(𝐵)=𝑃(𝐵|𝐴)𝑃(𝐴)+𝑃(𝐵|𝐴′)𝑃(𝐴′)
这就是全概率公式。它的含义是,如果A和A'构成样本空间的一个划分,那么事件B的概率,就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。
贝叶斯推断
对条件概率公式进行变形,可以得到如下形式:

我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
后验概率 = 先验概率x调整因子
朴素贝叶斯推断
贝叶斯和朴素贝叶斯的概念是不同的,区别就在于“朴素”二字,朴素贝叶斯对条件概率分布做了条件独立性的假设。
根据贝叶斯定理,后验概率 P(a|X) 可以表示为:
-
P(X|a) 是给定类别 ( a ) 下观测到特征向量 $X=(x_1, x_2, ..., x_n) $的概率;
-
P(a) 是类别 a 的先验概率;
-
P(X) 是观测到特征向量 X 的边缘概率,通常作为归一化常数处理。
又因,朴素贝叶斯分类器的关键假设是特征之间的条件独立性, 因此,我们可以将联合概率 P(X|a) 分解为各个特征的概率乘积:
将这个条件独立性假设应用于贝叶斯公式,我们得到:
这样,朴素贝叶斯分类器就可以通过计算每种可能类别的条件概率和先验概率,然后选择具有最高概率的类别作为预测结果。
| 纹理 | 色泽 | 鼔声 | 类别 | |
|---|---|---|---|---|
| 1 | 清晰 | 清绿 | 清脆 | 好瓜 |
| 2 | 模糊 | 乌黑 | 浊响 | 坏瓜 |
| 3 | 模糊 | 清绿 | 浊响 | 坏瓜 |
| 4 | 清晰 | 乌黑 | 沉闷 | 好瓜 |
| 5 | 清晰 | 清绿 | 浊响 | 好瓜 |
| 6 | 模糊 | 乌黑 | 沉闷 | 坏瓜 |
| 7 | 清晰 | 乌黑 | 清脆 | 好瓜 |
| 8 | 模糊 | 清绿 | 沉闷 | 好瓜 |
| 9 | 清晰 | 乌黑 | 浊响 | 坏瓜 |
| 10 | 模糊 | 清绿 | 清脆 | 好瓜 |
| 11 | 清晰 | 清绿 | 沉闷 | ? |
| 12 | 模糊 | 乌黑 | 浊响 | ? |
按例中第12个瓜来判断
首先计算样本中好瓜和坏瓜的概率(10个瓜中有6个好瓜,4个坏瓜)
P(好瓜)=0.6
P(坏瓜)=0.4
--------------
P(纹理清晰)=0.5
P(纹理模糊)=0.5
--------------
P(色泽清绿)=0.5
P(色泽乌黑)=0.5
--------------
P(声音清脆)=0.3
P(声音沉闷)=0.3
P(声音浊响)=0.4
-----------------
第12个瓜的特征是(纹理模糊,色泽乌黑,声音浊响)
则:
P(纹理模糊|好瓜)=1/3
P(纹理模糊|坏瓜)=3/4
P(色泽乌黑|好瓜)=1/3
P(色泽乌黑|坏瓜)=3/4
P(声音浊响|好瓜)=1/3
P(声音浊响|坏瓜)=3/4
---------------------
P(好瓜)=P(纹理模糊|好瓜)*P(色泽乌黑|好瓜)*P(声音浊响|好瓜)*P(好瓜)/p(纹理模糊,色泽乌黑,声音浊响)=((1/3)*(1/3)*(1/3)*0.6)/p(纹理模糊,色泽乌黑,声音浊响)
P(坏瓜)=P(纹理模糊|坏瓜)*P(色泽乌黑|坏瓜)*P(声音浊响|坏瓜)*P(坏瓜)/p(纹理模糊,色泽乌黑,声音浊响)=((3/4)*(3/4)*(3/4)*0.4)/p(纹理模糊,色泽乌黑,声音浊响)P(好瓜) < P(坏瓜)
故第12个瓜推断为坏瓜拉普拉斯平滑系数
些事件或特征可能从未出现过,这会导致它们的概率被估计为零。然而,在实际应用中,即使某个事件或特征没有出现在训练集中,也不能完全排除它在未来样本中出现的可能性。拉普拉斯平滑技术可以避免这种“零概率陷阱”
公式为:

一般α取值1,m的值为总特征数量
例如:
sklearn API
sklearn.naive_bayes.MultinomialNB()
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)sklearn 示例
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
# 加载数据
x,y = load_iris(return_X_y=True)
# 分割
x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.8,random_state=42,stratify=y)
# 创建模型
bayes = MultinomialNB()
# 训练
bayes.fit(x_train,y_train)
# 评估
score = bayes.score(x_test,y_test)
print(score)
# 预测
y_predict=bayes.predict([[2,5,3,5]])
print(y_predict) 
决策树-分类
概念
树结构,通过条件判断而进行分支选择的节点。
基于信息增益决策树的建立
信息增益决策树倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息,算法只能对描述属性为离散型属性的数据集构造决策树。
(1) 信息熵
信息熵描述的是不确定性。信息熵越大,不确定性越大。信息熵的值越小,则D的纯度越高。
假设样本集合D共有N类,第k类样本所占比例为Pk,则D的信息熵为![]()
(2) 信息增益
信息增益是一个统计量,用来描述一个属性区分数据样本的能力。信息增益越大,那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量, 信息增益公式:
![]()
(3) 信息增益决策树建立步骤
第一步,计算根节点的信息熵
上表根据是否贷款把样本分成2类样本,"是"占4/6=2/3, "否"占2/6=1/3,
所以 ![]()
第二步,计算属性的信息增益
计算各特征的信息增益
第三步, 划分属性
对比属性信息增益,选择最大的特征作为第一个节点,将剩下的特征及目标继续重复计算信息熵,得到最大的作为第二个,以此类推。
基于基尼指数决策树的建立
基尼指数(Gini Index)是决策树算法中用于评估数据集纯度的一种度量,基尼指数衡量的是数据集的不纯度,或者说分类的不确定性。在构建决策树时,基尼指数被用来决定如何对数据集进行最优划分,以减少不纯度。
基尼指数的计算
对于一个二分类问题,如果一个节点包含的样本属于正类的概率是 (p),则属于负类的概率是 (1-p)。那么,这个节点的基尼指数 (Gini(p)) 定义为:
对于多分类问题,如果一个节点包含的样本属于第 k 类的概率是 ,则节点的基尼指数定义为:
-
当一个节点的所有样本都属于同一类别时,基尼指数为 0,表示纯度最高。
-
当一个节点的样本均匀分布在所有类别时,基尼指数最大,表示纯度最低。
案例:

首先工资有两个取值,分别是0和1。当工资=1时,有3个样本。
因此:![]()
同时,在这三个样本中,工作都是好。
故:![]()
同理,当工资=0时,有5个样本,在这五个样本中,工作有3个是不好,2个是好。
![]()
两个式子相加得:

得到工资的基尼系数
同理可算出压力的基尼系数,平台的基尼系数


根据基尼指数最小准则, 我们优先选择工资或者平台=0作为D的第一特征。
再将剩下的特征再进行相同计算,再选择一个基尼系数最小的作为第二特征
sklearn API

示例
葡萄酒分类
用决策树对葡萄酒进行分类
from sklearn.datasets import load_wine
from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_splitwine = load_wine()
x = wine.data
y = wine.target# 分割,stratify可指定按谁分割。
x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.8,random_state=42,stratify=y)
# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 模型,criterion='entropy'表示用信息熵来计算,criterion='gini'表示用基尼系数来计算,默认值用基尼系数
decter = DecisionTreeClassifier(criterion='entropy')
# 训练
decter.fit(x_train,y_train)
# 评估
score = decter.score(x_test,y_test)
print(score)
# 预测
y_predict = decter.predict([[1,2,3,4,5,5,7,8,9,6,4,8,9]])
print(y_predict)
# 可视化
export_graphviz(decter, out_file="./model/wine1.dot", feature_names=wine.feature_names)![]()
下列是可视化文件:

相关文章:

机器学习(贝叶斯算法,决策树)
朴素贝叶斯分类 贝叶斯分类理论 假设现有两个数据集,分为两类 我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中红色圆点表示的类别)的概率,用p2(x,y)表示数据点(x,y)属于类别2(图中蓝色三角形表示的类别)的概率,那么对于一个新数据点(x,y)…...

实验十三 生态安全评价
1 背景及目的 生态安全是生态系统完整性和健康性的整体反映,完整健康的生态系统具有调节气候净化污染、涵养水源、保持水土、防风固沙、减轻灾害、保护生物多样性等功能。维护生态安全对于人类生产、生活、健康及可持续发展至关重要。随着城市化进程的不断推进&…...

二级等保要求及设备有哪些?
《网络安全法》规定我国信息系统实际等级保护制度,不同等保等级要求不同: 二级等保(指导保护级):等级保护对象受到破坏后,会对公民、法人和其他组织的合法权益产生严重损害,或者对社会秩序和公…...
无人机的动力系统节能——CKESC电调小课堂12
1.优化电机和螺旋桨配置 精准匹配:根据无人机的设计用途和负载要求,精确选择电机和螺旋桨。确保电机的功率、扭矩等参数与螺旋桨的尺寸、螺距等完美匹配。例如,对于轻型航拍无人机,选用功率合适的小尺寸电机搭配高效的小螺旋桨&a…...
)
人机打怪小游戏(非常人机)
按q攻击 按箭头进行控制 玩家是 怪是* 攻击是^ #include<bits/stdc.h> #include<Windows.h> #include<conio.h> #define fr(i,a,b) for(int ia;i<b;i) #define rd(a,b) rand()%(b-a1)a using namespace std; int x16,y21,dx[4]{-1,0,1,0},dy[4]{0,…...

SpringBoot 集成 Sharding-JDBC(一):数据分片
在深入探讨 Sharding-JDBC 之前,建议读者先了解数据库分库分表的基本概念和应用场景。如果您还没有阅读过相关的内容,可以先阅读我们之前的文章: 关系型数据库海量数据存储策略-CSDN博客 这篇文章将帮助您更好地理解分库分表的基本原理和实现…...

django-ninja 实现cors跨域请求
要在Django-Ninja项目中实现跨域(CORS),你可以使用django-cors-headers库,这是一个专门用于处理跨域资源共享(CORS)问题的Django应用程序。以下是具体的步骤和配置: 安装依赖: 使用p…...

【论文阅读】InstructPix2Pix: Learning to Follow Image Editing Instructions
摘要: 提出了一种方法,用于教导生成模型根据人类编写的指令进行图像编辑:给定一张输入图像和一条书面指令,模型按照指令对图像进行编辑。 由于为此任务获取大规模训练数据非常困难,我们提出了一种生成配对数据集的方…...

常用在汽车PKE无钥匙进入系统的高度集成SOC芯片:CSM2433
CSM2433是一款集成2.4GHz频段发射器、125KHz接收器和8位RISC(精简指令集)MCU的SOC芯片,用在汽车PKE无钥匙进入系统里。 什么是汽车PKE无钥匙进入系统? 无钥匙进入系统具有无钥匙进入并且启动的功能,英文名称是PKE&…...

【第四课】rust声明式宏理解与实战
目录 前言 理解宏 实战宏 前言 上一课在介绍vector时,我们再一次提到了rust中的宏,在初始化vector时使用了vec!宏,当时补了一句有机会会好好说明一下rust中的宏,并且写一个hashmap宏来初始化hashmap。想了想一直介绍基本语法还…...

渗透测试--Linux下的文件传输方法
渗透测试过程中,我们经常会需要文件传输,本文主要探讨Linux主机上我们对文件传输的方法。 编码方式 Linux 检查MD5 md5sum id_rsa Linux Base64 编码/解码 编码 cat id_rsa |base64 -w 0;echo 解码 echo -n LS0tLS1CRUdJTiBPUEVOU1NIIFBSSVZBVE…...
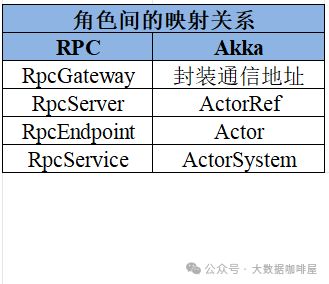
浅议Flink中的通讯工具: Akka
在Flink中,各个组件之间需要频繁交换数据和控制信息。Flink选择了基于Actor模型的Akka框架作为通信基础。 Akka是什么 Actor模型 Actor模型是用于单个进程中并发的场景。 在Actor模型中: ActorSystem负责管理actor生命周期 将每个实体视为独立的 Ac…...
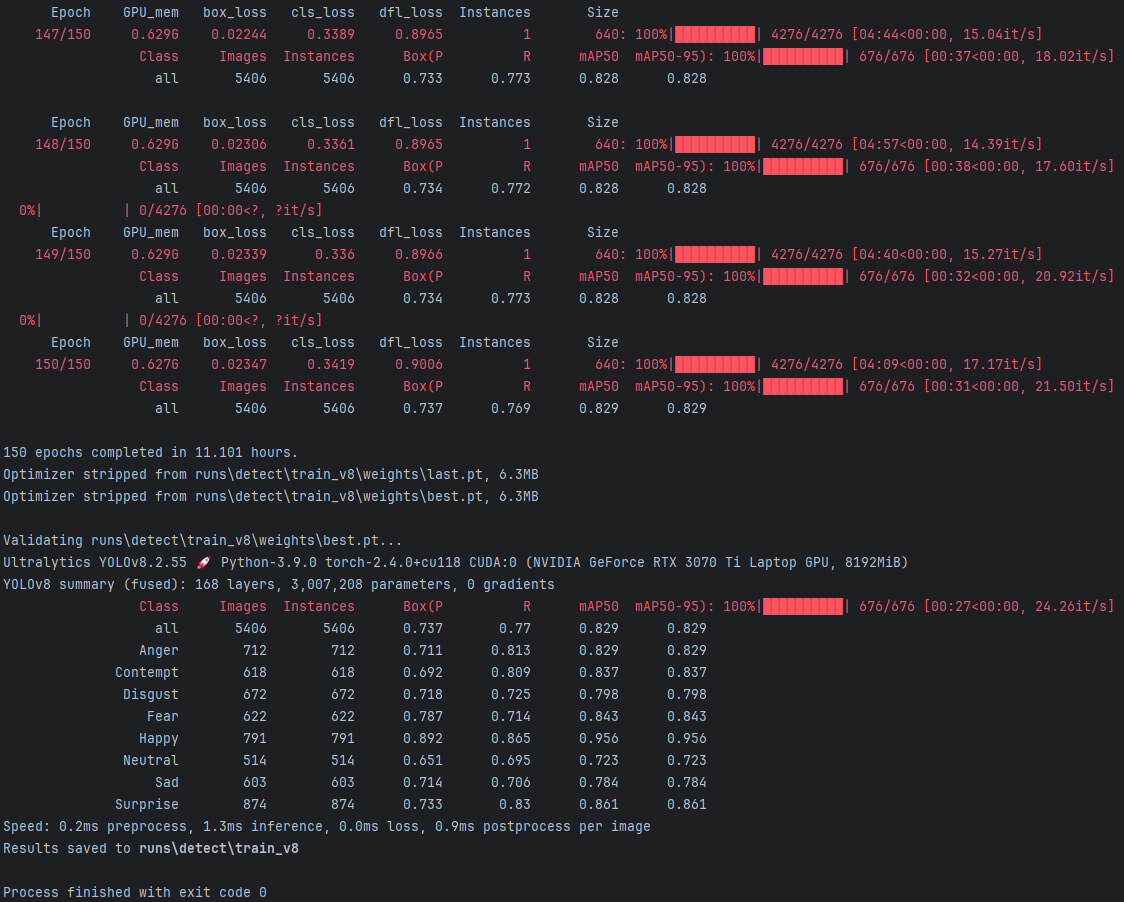
基于YOLOv8深度学习的独居老人情感状态监护系统(PyQt5界面+数据集+训练代码)
本研究提出了一种创新的独居老人情感状态监护系统,基于YOLOV8深度学习模型,旨在通过对老年人面部表情的实时监测与分析,来精准识别其情感变化,从而提高独居老人的生活质量,确保其心理健康。本系统通过整合先进的YOLOV8…...

Qt添加外部库:静态库和动态库,批量添加头文件
Qt添加外部库需要知道库文件的位置才能正确链接,如果是静态库,要确保LIBS变量中包含正确的库文件路径和库文件名;如果是动态库,除了库路径外,还需要考虑动态库的加载路径。在 Windows 下,可以将动态库所在路径添加到系…...

Unity类银河战士恶魔城学习总结(P132 Merge skill tree with skill Manager 把技能树和冲刺技能相组合)
【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili 教程源地址:https://www.udemy.com/course/2d-rpg-alexdev/ 本章节实现了解锁技能后才可以使用技能,先完成了冲刺技能的锁定解锁 Dash_Skill.cs using System.Collections; using System…...

Docker入门之Windows安装Docker初体验
在之前我们认识了docker的容器,了解了docker的相关概念:镜像,容器,仓库:面试官让你介绍一下docker,别再说不知道了 之后又带大家动手体验了一下docker从零开始玩转 Docker:一站式入门指南&#…...

DNS实验作业
实验要求 1.搭建dns服务器能够对自定义的正向或者反向域完成数据解析查询。 2.配置从DNS服务器,对主dns服务器进行数据备份。 实验步骤: 1.关闭防护墙 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2.正向解析 [rootlo…...

CSS回顾-CSS选择器详解
一、引言 我来填坑啦!之前在CSS基础知识详解中介绍过,CSS 是一门基于规则的语言。是由选择器与样式信息组成:选择器 {样式信息}。CSS 选择器是 CSS 规则的关键,能精准定位 HTML 元素,CSS3 新增选择器更是增强了设计能…...

FFMPEG录像推流时遇到的问题
FFMPEG录像推流时遇到的问题,记录一下供大参考 1. ret avformat_write_header( ofmt_ctx, NULL ); 执行写入头后,所有的流的时间基都会被内部重新设置,所以并不你想象的把原来的时间直接入到avPACKET中就可以发送了。必须要把你每个流的P…...
)
【STM32+K210项目】基于K210智能人脸识别+车牌识别系统(完整工程资料源码)
运行效果: 基于K210的智能人脸与车牌识别系统工程 目录: 运行效果: 目录: 前言: 一、国内外研究现状与发展趋势 二、相关技术基础 2.1 人脸识别技术 2.2 车牌识别技术 三、智能小区门禁系统设计 3.1 系统设计方案 3.2 系统设计目标 3.3 智能小区门禁系统硬件设计 3.3.1 控…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
