Leetcode打卡:新增道路查询后的最短距离II
执行结果:通过

题目:3244 新增道路查询后的最短距离II
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径的长度。
所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
示例 1:
输入: n = 5, queries = [[2, 4], [0, 2], [0, 4]]
输出: [3, 2, 1]
解释:

新增一条从 2 到 4 的道路后,从 0 到 4 的最短路径长度为 3。

新增一条从 0 到 2 的道路后,从 0 到 4 的最短路径长度为 2。

新增一条从 0 到 4 的道路后,从 0 到 4 的最短路径长度为 1。
示例 2:
输入: n = 4, queries = [[0, 3], [0, 2]]
输出: [1, 1]
解释:

新增一条从 0 到 3 的道路后,从 0 到 3 的最短路径长度为 1。

新增一条从 0 到 2 的道路后,从 0 到 3 的最短路径长度仍为 1。

提示:
3 <= n <= 1051 <= queries.length <= 105queries[i].length == 20 <= queries[i][0] < queries[i][1] < n1 < queries[i][1] - queries[i][0]- 查询中不存在重复的道路。
- 不存在两个查询都满足
i != j且queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
代码以及解题思路
代码:
class Solution:def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:st = LazySegmentTree(n)ans = []for l, r in queries:st.update(1,1,n,l+2,r, 0)ans.append(st.cnt[1]-1)return ansclass LazySegmentTree:def __init__(self, n: int):self.cnt = [0] * (4 * n)self.todo = [-1] * (4 * n)self.build(1,1,n)# 初始化线段树 o,l,r=1,1,ndef build(self, o: int, l: int, r: int) -> None:if l == r:self.cnt[o] = 1returnm = (l + r) >> 1self.build(o * 2, l, m)self.build(o * 2 + 1, m + 1, r)self.maintain(o)def maintain(self, o: int) -> None:self.cnt[o] = self.cnt[o * 2] + self.cnt[o * 2 + 1]def do(self, o: int, val: int) -> None:self.cnt[o] = valself.todo[o] = valdef spread(self, o: int) -> None:v = self.todo[o]if v == 0:self.do(o * 2, v)self.do(o * 2 + 1, v)self.todo[o] = -1def update(self, o: int, l: int, r: int, L: int, R: int, val: int) -> None:if L <= l and r <= R:self.do(o, val)returnself.spread(o)m = (l + r) >> 1if m >= L:self.update(o * 2, l, m, L, R, val)if m < R:self.update(o * 2 + 1, m + 1, r, L, R, val)self.maintain(o)def query(self, o: int, l: int, r: int, L: int, R: int) -> int:if L <= l and r <= R:return self.cnt[o]self.spread(o)m = (l + r) >> 1res = 0if L <= m:res = self.query(o * 2, l, m, L, R)if m < R:res = max(res, self.query(o * 2 + 1, m + 1, r, L, R))return res解题思路:
- 初始化线段树:
- 创建一个
LazySegmentTree实例,其大小为4n(因为线段树通常需要一个额外的空间来存储内部节点)。 - 初始化
cnt数组来存储每个节点的区间内未访问元素的数量。 - 初始化
todo数组来存储延迟的更新操作。 - 调用
build方法来构建线段树,初始时所有元素都是未访问的,所以每个叶子节点的cnt值都设为 1(表示该位置是未访问的)。
- 创建一个
- 处理查询:
- 对于每个查询
(l, r),调用update方法将索引从l+2到r(注意这里的l+2是因为题目可能有特定的索引约定,比如索引 0 和 1 被视为特殊情况,或者为了避免边界问题)之间的所有元素标记为已访问(即将其cnt值更新为 0)。 - 在每次更新后,通过查看根节点的
cnt值(即整个数组的未访问元素数量)减 1 来计算最近的未访问元素与数组起始位置的距离。这是因为每次更新都会使得一个元素从未访问变为已访问,而根节点的cnt值反映了整个数组中未访问元素的数量。减 1 是因为索引是从 0 开始的,而我们需要的是距离,所以需要将计数器的值转换为实际的索引距离(这里假设数组中的元素是连续排列的,没有空缺)。
- 对于每个查询
- 线段树的操作:
build方法用于构建线段树,初始化每个叶子节点的cnt值。maintain方法用于维护节点的cnt值,确保它反映了其子节点的cnt值之和。do方法用于立即更新节点的cnt值和todo值。spread方法用于将延迟的更新操作传播到子节点。update方法用于执行区间更新操作,使用延迟技术来优化性能。query方法虽然在这段代码中未使用,但通常用于查询区间内的某些信息(如最大值、最小值等)。
相关文章:

Leetcode打卡:新增道路查询后的最短距离II
执行结果:通过 题目:3244 新增道路查询后的最短距离II 给你一个整数 n 和一个二维整数数组 queries。 有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向道路通往城市 i 1( 0 < i < n - 1&…...

Spring Web入门练习
加法计算器 约定前后端交互接⼝ 约定 "前后端交互接⼝" 是进⾏ Web 开发中的关键环节. 接⼝⼜叫 API(Application Programming Interface), 我们⼀般讲到接⼝或者 API,指的都是同⼀个东西. 是指应⽤程序对外提供的服务的描述, ⽤于交换信息…...

计算机毕业设计 | SpringBoot+vue汽车资讯网站 汽车购买咨询管理系统(附源码+论文)
1,绪论 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理汽车资讯网站的相关信息成为必然…...

stm32下的ADC转换(江科协 HAL版)
十二. ADC采样 文章目录 十二. ADC采样12.1 ADC的采样原理12.2 STM32的采样基本过程1.引脚与GPIO端口的对应关系2.ADC规则组的四种转换模式(**)2.2 关于转换模式与配置之间的关系 12.3 ADC的时钟12.4 代码实现(ADC单通道 & ADC多通道)1. 单通道采样2. 多通道采样 19.ADC模数…...

解决IntelliJ IDEA的Plugins无法访问Marketplace去下载插件
勾选Auto-detect proxy setting并填入 https://plugins.jetbrains.com 代理URL,可以先做检查连接:...

react 如何修改弹出的modal的标题
原来标题的样子: 修改为: 实现方式: <Modal title<span>股价趋势/{this.state.pccode}</span> visible{this.state.isPriceModalOpen} style{{ top: 20 }} width{1320} height{400} footer{null} onCancel{()>this.hideMo…...

C#中的二维数组的应用:探索物理含义与数据结构的奇妙融合
在C#编程中,二维数组(或矩阵)是一种重要的数据结构,它不仅能够高效地存储和组织数据,还能通过其行、列和交叉点(备注:此处相交处通常称为“元素”或“单元格”,代表二维数组中的一个…...

HTML5拖拽API学习 托拽排序和可托拽课程表
文章目录 前言拖拽API核心概念拖拽式使用流程例子注意事项综合例子🌰 可拖拽课程表拖拽排序 前言 前端拖拽功能让网页元素可以通过鼠标或触摸操作移动。HTML5 提供了标准的拖拽API,简化了拖放操作的实现。以下是拖拽API的基本使用指南: 拖拽…...
)
内容补充页(相关公式解释)
from 学习日记_20241117_聚类方法(高斯混合模型) 学习日记_20241117_聚类方法(高斯混合模型) 公式 P ( Z k ) π k P(Zk) \pi_k P(Zk)πk 在高斯混合模型 (GMM) 中,公式 P ( Z k ) π k P(Zk) \pi_k P(Zk…...

vue中动态渲染静态图片资源
不报错且f12查看元素的时候,显示的src说明已经渲染到html的src上,但是就是不显示在页面上 原因 在vue上,动态渲染静态图片资源(比如从assets文件夹加载的图片)需要注意打包工具对静态资源的解析方式 由于vue2的脚手…...

管伊佳ERP,原名华夏ERP,一个简约易上手的国产ERP系统
JSH_ERP(管伊佳ERP)是一款开源、模块化的企业资源计划系统,旨在为中小企业提供高效的管理工具。它基于SpringBoot框架和SaaS模式,支持进销存、财务、生产等业务模块,包括零售、采购、销售、仓库和报表管理。 核心特点…...

学习虚幻C++开发日志——委托(持续更新中)
委托 官方文档:Delegates and Lamba Functions in Unreal Engine | 虚幻引擎 5.5 文档 | Epic Developer Community | Epic Developer Community 简单地说,委托就像是一个“函数指针”,但它更加安全和灵活。它允许程序在运行时动态地调用不…...
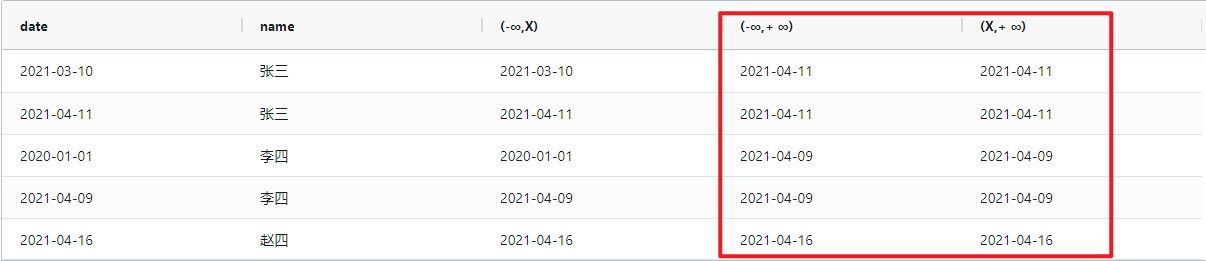
开窗函数 - first_value/last_value
1、开窗函数是什么? 开窗函数用于为行定义一个窗口(这里的窗口是指运算将要操作的行的集合),它对一组值进行操作,不需要使用 GROUP BY 子句对数据进行分组,能够在同一行中同时返回基础行的列和聚合列。 2、…...

「一」HarmonyOS端云一体化概要
关于作者 白晓明 宁夏图尔科技有限公司董事长兼CEO、坚果派联合创始人 华为HDE、润和软件HiHope社区专家、鸿蒙KOL、仓颉KOL 华为开发者学堂/51CTO学堂/CSDN学堂认证讲师 开放原子开源基金会2023开源贡献之星 「目录」 「一」HarmonyOS端云一体化概要 「二」体验HarmonyOS端云一…...

nodejs21: 快速构建自定义设计样式Tailwind CSS
Tailwind CSS 是一个功能强大的低级 CSS 框架,只需书写 HTML 代码,无需书写 CSS,即可快速构建美观的网站。 1. 安装 Tailwind CSS React 项目中安装 Tailwind CSS: 1.1 安装 Tailwind CSS 和相关依赖 安装 Tailwind CSS: npm…...

从JSON数据提取嵌套字段并转换为独立列的简洁方法
从JSON数据提取嵌套字段并转换为独立列的简洁方法 在数据处理和数据分析的日常工作中,我们经常遇到复杂的嵌套数据结构,特别是嵌入在JSON字段中的数据。这些数据往往需要解析并展开成独立的列,以便后续分析和建模。本文将详细介绍如何在Pyth…...

湘潭大学软件工程算法设计与分析考试复习笔记(四)
回顾 湘潭大学软件工程算法设计与分析考试复习笔记(一)湘潭大学软件工程算法设计与分析考试复习笔记(二)湘潭大学软件工程算法设计与分析考试复习笔记(三) 前言 现在是晚上十一点,我平时是十…...

特征交叉-DeepCross Network学习
一 tensorflow官方实现 tensorflow的官方实现已经是V2版本 class Cross(tf.keras.layers.Layer):"""Cross Layer in Deep & Cross Network to learn explicit feature interactions.Args:projection_dim: int,低秩矩阵的维度,应该小…...
stm32cubemx+VSCODE+GCC+makefile 开发环境搭建
title: stm32cubemxVSCODEGCCmakefile 开发环境搭建 tags: FreertosHalstm32cubeMx 文章目录 内容往期内容导航第一步准备环境vscode 插件插件配置点灯 内容 往期内容导航 第一步准备环境 STM32CubeMXVSCODEMinGWOpenOcdarm-none-eabi-gcc 然后把上面下载的软件 3 4 5 bin 文…...

Go语言中的Defer机制详解与示例
在Go语言中,defer是一个关键字,用于确保资源的清理和释放,特别是在函数中创建的资源。defer语句会将其后的函数调用推迟到包含它的函数即将返回时执行。这使得defer成为处理文件关闭、数据库连接释放、解锁等资源清理操作的理想选择。 Defer…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
