C++【二叉树进阶(二叉搜索树)】
文章目录
- 前言
- 1、二叉搜索树
- 1-1、 二叉搜索树概念
- 2、二叉搜索树操作
- 2-1、树和节点的基本框架
- 2-2、二叉搜索树的查找
- 2-3、中序遍历
- 2-4、二叉搜索树的插入
- 2-5、二叉搜索树的删除
- 3、二叉搜索树的模拟实现
- 3-1、循环版本
- 3-2、递归版本
- 4、二叉搜索树的应用
- 4-1、K模型
- 4-2、KV模型
- 4-3、KV模型的代码样例
- 5、二叉搜索树的性能分析
- 6、总结
前言
二叉树在前面C数据结构阶段已经讲过,本节取名二叉树进阶是因为:
- map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
- 二叉搜索树的特性了解,有助于更好的理解map和set的特性
- 二叉树中部分面试题稍微有点难度,在前面讲解大家不容易接受,且时间长容易忘
- 有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组,非常麻烦。
因此本节借二叉树搜索树,对二叉树部分进行收尾总结。
1、二叉搜索树
1-1、 二叉搜索树概念
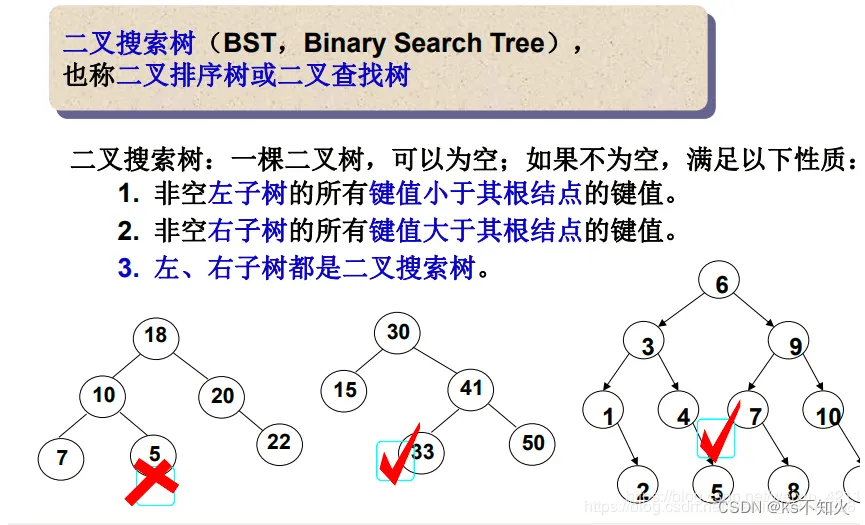
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
2、二叉搜索树操作
2-1、树和节点的基本框架
template<class k>
class BSTreeNode //结构体——包含节点,左指针和右指针
{
public:BSTreeNode<k>* _left;//节点的左指针BSTreeNode<k>* _right;//节点的右指针k _key;//节点的值BSTreeNode(const k& key)//构造函数,不写的话new生成不了节点:_left(nullptr), _right(nullptr),_key(key){}
};template<class k>
class BSTree
{typedef BSTreeNode<k> Node;//这里重定义节点,方便后面的操作
public:Node* _root = nullptr;//根节点
2-2、二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。
bool Find(const k& key)//查找key值
{Node* cur = _root;while (cur){if (cur->_key < key)//如果查找的值大,向右继续查找{cur = cur->_right;}else if (cur->_key > key)//如果查找的值小,向左继续查找{cur = cur->_left;}else{return true;}}return false;
}
2-3、中序遍历
对于二叉搜索树而言,每一个节点的左子树值都比该节点的值小,右子树的值都比该节点的值要大。所以,中序遍历二叉搜索树是可以得到一个升序序列的!
void _InOrder(Node * root)//中序遍历
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);
}
2-4、二叉搜索树的插入
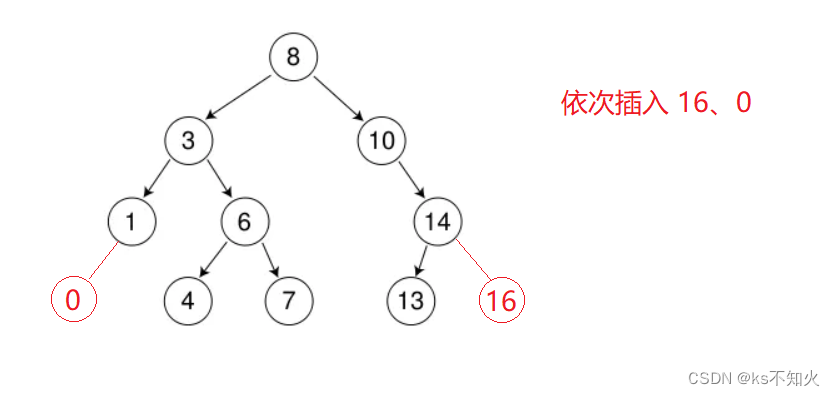
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
bool Insert(const k& key)//插入
{if (_root == nullptr)//空树直接new节点就行{_root = new Node(key);return true;}Node* cur = _root;//cur从根开始找Node* parent = nullptr;//记录父节点while (cur){if (cur->_key < key)//我比你大,就向右找{parent = cur;cur = cur->_right;}else if (cur->_key > key)//我比你小,就向左找{parent = cur;cur = cur->_left;}else不存在一样的,二叉搜索树不允许有重复的值{return false;}}cur = new Node(key);//到这里就找到了我们要插入节点的为止,我们new(key)if (parent->_key < key)//如果父亲的_key值小于我们,就链接在父节点的右边{parent->_right = cur;}else//如果父亲的_key值大于我们,就链接在父节点的左边{parent->_left = cur;}return true;
}
2-5、二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来:
b. 右子树为空
c. 左子树为空
d. 左右子树都不为空
因此真正的删除过程如下:
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小:右子树的最左值,也就是右子树最小节点),用它的值填补到被删除节点 中,再来处理该结点的删除问题–替换法删除
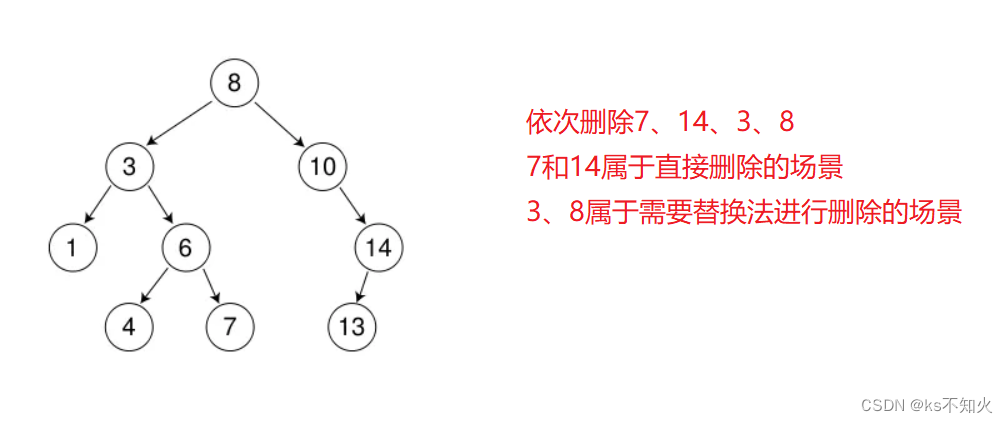
情况b:
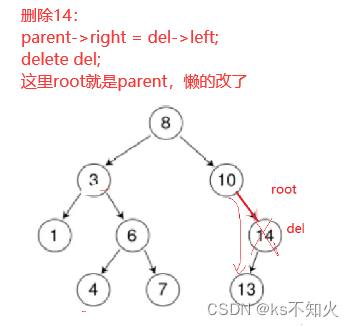
情况c:
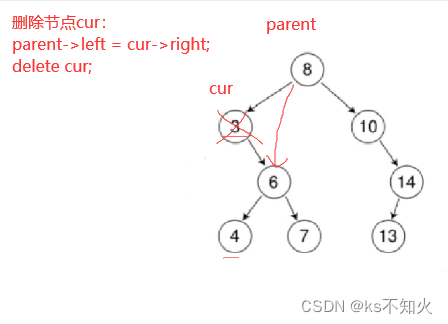
情况d:
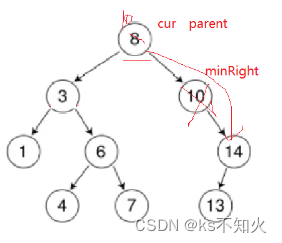
我们来看看代码:
bool Erase(const k& key)//删除
{Node* cur = _root;//cur向下面走,找删除节点的key值Node* parent = nullptr;//parent就是删除节点的父节点——也就是cur的父节点while (cur){if (cur->_key < key)//老规矩,比你大向右找{parent = cur;//这个时候父节点要更新cur = cur->_right;}else if (cur->_key > key)//比你小向左找{parent = cur;//同理cur = cur->_left;}else到这里就找到了{//三种情况:// 1、左为空// 2、右为空// 3、左右都不为空,替换删除if (cur->_left == nullptr)// 1、左为空{//if(parent == nullptr)if (cur == _root)//如果是一颗单枝树,删除根节点,parent就为空了,那么parent->_left等操作违法{//这里的cur和_root都是根节点了,我们让_root等于_root的右节点,这样下面删除cur,//也就是删除原来的根节点了,而_root现在变成了原来树的右子树的第一个节点_root = cur->_right;}else{if (parent->_left == cur)//如果父节点的左边是cur,删除cur之后,cur的右子树链接父亲左边{parent->_left = cur->_right;}else//如果父节点的右边是cur,删除cur之后,cur的右子树链接父亲右边{parent->_right = cur->_right;}}delete cur;//这个时候删除就没问题了}else if (cur->_right == nullptr)// 2、右为空{//if(parent == nullptr)if (cur == _root)//如果是一颗单枝树,删除根节点,parent就为空了,那么parent->_left等操作违法{//这里的cur和_root都是根节点了,我们让_root等于_root的左节点,这样下面删除cur,//也就是删除原来的根节点了,而_root现在变成了原来树的左子树的第一个节点_root = cur->_left;}else{if (parent->_left == cur)//如果父节点的左边是cur,删除cur之后,cur的右左子树链接父亲左边{parent->_left = cur->_left;}else//如果父节点的右边是cur,删除cur之后,cur的左子树链接父亲右边{parent->_right = cur->_left;}}delete cur;}else// 3、左右都不为空,替换删除{//这里parent不能初始化为nullptr,如果删除的cur是根,那么parent就不会进入while循环进行更新//那么parent就一直为空,下面parent->_left等操作就非法了!!!Node* parent = cur; //parent就是替换完之后,删除节点的父节点Node* min = cur->_right;//min是右子树的最小值while (min->_left)//找右子树最小的数,(也可以找左子树最大的数,但是这样太麻烦了)//while (min && min->_left)//这里不用这么写,因为前提条件就是cur删除节点左右都不为空{parent = min;min = min->_left;}cur->_key = min->_key;//把右子树最小值给给curif (parent->_left == min)//min是最左值,所以没有左子树,只有右子树需要托孤{parent->_left = min->_right;}else{parent->_right = min->_right;}delete min;}return true;}}return false;
}
3、二叉搜索树的模拟实现
这里有两个版本:循环和递归
我们只用掌握一个版本就可以了!
3-1、循环版本
BSTree.h:循环版本
#pragma once
///循环版本
template<class k>
class BSTreeNode //结构体——包含节点,左指针和右指针
{
public:BSTreeNode<k>* _left;BSTreeNode<k>* _right;k _key;BSTreeNode(const k& key)//构造函数,不写的话new生成不了节点:_left(nullptr), _right(nullptr),_key(key){}
};template<class k>
class BSTree
{typedef BSTreeNode<k> Node;
public:bool Insert(const k& key)//插入{if (_root == nullptr)//空树直接new节点就行{_root = new Node(key);return true;}Node* cur = _root;//cur从根开始找Node* parent = nullptr;//记录父节点while (cur){if (cur->_key < key)//我比你大,就向右找{parent = cur;cur = cur->_right;}else if (cur->_key > key)//我比你小,就向左找{parent = cur;cur = cur->_left;}else不存在一样的,二叉搜索树不允许有重复的值{return false;}}cur = new Node(key);//到这里就找到了我们要插入节点的为止,我们new(key)if (parent->_key < key)//如果父亲的_key值小于我们,就链接在父节点的右边{parent->_right = cur;}else//如果父亲的_key值大于我们,就链接在父节点的左边{parent->_left = cur;}return true;}bool Find(const k& key)//查找key值{Node* cur = _root;while (cur){if (cur->_key < key)//如果查找的值大,向右继续查找{cur = cur->_right;}else if (cur->_key > key)//如果查找的值小,向左继续查找{cur = cur->_left;}else{return true;}}return false;}bool Erase(const k& key)//删除{Node* cur = _root;//cur向下面走,找删除节点的key值Node* parent = nullptr;//parent就是删除节点的父节点——也就是cur的父节点while (cur){if (cur->_key < key)//老规矩,比你大向右找{parent = cur;//这个时候父节点要更新cur = cur->_right;}else if (cur->_key > key)//比你小向左找{parent = cur;//同理cur = cur->_left;}else到这里就找到了{//三种情况:// 1、左为空// 2、右为空// 3、左右都不为空,替换删除if (cur->_left == nullptr)// 1、左为空{//if(parent == nullptr)if (cur == _root)//如果是一颗单枝树,删除根节点,parent就为空了,那么parent->_left等操作违法{//这里的cur和_root都是根节点了,我们让_root等于_root的右节点,这样下面删除cur,//也就是删除原来的根节点了,而_root现在变成了原来树的右子树的第一个节点_root = cur->_right;}else{if (parent->_left == cur)//如果父节点的左边是cur,删除cur之后,cur的右子树链接父亲左边{parent->_left = cur->_right;}else//如果父节点的右边是cur,删除cur之后,cur的右子树链接父亲右边{parent->_right = cur->_right;}}delete cur;//这个时候删除就没问题了}else if (cur->_right == nullptr)// 2、右为空{//if(parent == nullptr)if (cur == _root)//如果是一颗单枝树,删除根节点,parent就为空了,那么parent->_left等操作违法{//这里的cur和_root都是根节点了,我们让_root等于_root的左节点,这样下面删除cur,//也就是删除原来的根节点了,而_root现在变成了原来树的左子树的第一个节点_root = cur->_left;}else{if (parent->_left == cur)//如果父节点的左边是cur,删除cur之后,cur的右左子树链接父亲左边{parent->_left = cur->_left;}else//如果父节点的右边是cur,删除cur之后,cur的左子树链接父亲右边{parent->_right = cur->_left;}}delete cur;}else// 3、左右都不为空,替换删除{//这里parent不能初始化为nullptr,如果删除的cur是根,那么parent就不会进入while循环进行更新//那么parent就一直为空,下面parent->_left等操作就非法了!!!Node* parent = cur; //parent就是替换完之后,删除节点的父节点Node* min = cur->_right;//min是右子树的最小值while (min->_left)//找右子树最小的数,(也可以找左子树最大的数,但是这样太麻烦了)//while (min && min->_left)//这里不用这么写,因为前提条件就是cur删除节点左右都不为空{parent = min;min = min->_left;}cur->_key = min->_key;//把右子树最小值给给curif (parent->_left == min)//min是最左值,所以没有左子树,只有右子树需要托孤{parent->_left = min->_right;}else{parent->_right = min->_right;}delete min;}return true;}}return false;}void InOrder()//树的递归要使用根节点,根节点都是私有的,所以要通过嵌套的方法来调用{_InOrder(_root);cout << endl;}
private:void _InOrder(Node * root)//中序遍历{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;//根节点
};void Test1()//测试用例
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (const auto& e : a){t.Insert(e);}for (const auto& e : a){t.Erase(e);t.InOrder();}
}
3-2、递归版本
BSTreeR.h:递归版本
这里递归版本就不做过多解释了,重要代码都有注释
#pragma once
///递归版本
template<class k>
class BSTreeNode //结构体——包含节点,左指针和右指针
{
public:BSTreeNode<k>* _left;BSTreeNode<k>* _right;k _key;BSTreeNode(const k& key)//构造函数,不写的话new生成不了节点:_left(nullptr), _right(nullptr), _key(key){}
};template<class k>
class BSTreeR
{typedef BSTreeNode<k> Node;
public:BSTreeR():_root(nullptr){}~BSTreeR(){Destory(_root);_root = nullptr;}BSTreeR(BSTreeR<k>& t){this->_root = Cope(t._root);}BSTreeR operator=(BSTreeR<k> t){swap(this->_root, t._root);return *this;}bool InsertR(const k& key){return _InsertR(_root, key);}bool FindR(const k& key){return _FindR(_root, key);}bool EraseR(const k& key){return _EraseR(_root, key);}void InOrder()//树的递归要使用根节点,根节点都是私有的,所以要通过嵌套的方法来调用{_InOrder(_root);cout << endl;}private:void Destory(Node* root){if (root == nullptr)return;Destory(root->_left);Destory(root->_right);delete root;}Node* Cope(Node* root){if (root == nullptr)return nullptr;Node* newnode = new Node(root->_key);newnode->_left = Cope(root->_left);newnode->_right = Cope(root->_right);return newnode;}bool _InsertR(Node*& root, const k& key)//这里的root使用引用,这样就不用找parent节点了,root是指针的引用{if (root == nullptr)//空树直接new节点{root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}bool _FindR(Node* root, const k& key)//查找{if (root == nullptr)return false;if (root->_key < key)return _FindR(root->_right, key);else if (root->_key > key)return _FindR(root->_left, key);elsereturn true;}bool _EraseR(Node*& root, const k& key)//root是引用,是父节点指向删除节点的指针的引用{if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* dl = root;if (root->_right == nullptr)//如果删除的节点的右子树没有,就让父节点指向我的左{root = root->_left;}else if (root->_left == nullptr)//如果删除节点的左子树没有,就让父节点指向我的右{root = root->_right;}else{Node* minright = root->_right;//找右边最小值while (minright->_left){minright = minright->_left;}swap(root->_key, minright->_key);//交换两个值return _EraseR(root->_right, key);//交换完之后,删除的key值在右子树的最左边}delete dl;return true;}}void _InOrder(Node* root)//中序遍历{if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;//根节点
};void Test1()//测试用例
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTreeR<int> t;for (const auto& e : a){t.InsertR(e);}BSTreeR<int> copyt(t);copyt.InOrder();int b[] = { 15,54,545,4,46,65,464,84,9 };BSTreeR<int> ax;for (const auto& e : b){ax.InsertR(e);}ax.InOrder();copyt = ax;copyt.InOrder();for (const auto& e : a){t.EraseR(e);t.InOrder();}
}4、二叉搜索树的应用
4-1、K模型
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
·以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
·在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
4-2、KV模型
KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
·比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
·再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
4-3、KV模型的代码样例
样例1:将我们上面的二叉搜索树循环版本改为KV模型
//通过一个值找另一个值key value,也就是map(下一章节讲)
namespace KV
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;//这里的key值就是我们上面的key值,KV模型中,比较大小、查找等等操作都是与key值有关,但key值不能更改V _value;//_value我们用不上,value值可以更改BSTreeNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}};//BSTree<string, vector<string>> 字典查找template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool insert(const K& key, const V& value)//与上面没有什么差别,就是参数多了个value{if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}void Inorder(){_Inorder(_root);}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}private:void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key << ":" << root->_value << endl;_Inorder(root->_right);}Node* _root = nullptr;};
}
样例2:映射——通过key值找value
void Test2()
{string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };// 词库中单词都放进这个搜索树中// Key的搜索模型,判断在不在?// 场景:检查单词拼写是否正确/车库出入系统/...//K::BSTree<string> dict;// Key/Value的搜索模型,通过Key查找或修改ValueKV::BSTree<string, string> dict;dict.Insert("sort", "排序");dict.Insert("string", "字符串");dict.Insert("left", "左边");dict.Insert("right", "右边");string str;while (cin>>str){KV::BSTreeNode<string, string>* ret = dict.Find(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词" << endl;}}
}样例3:统计水果出现次数
void TestBSTree3()
{// 统计水果出现的次数string arr[] = { "苹果", "西瓜", "香蕉", "草莓","苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };KV::BSTree<string, int> countTree;for (auto e : arr){auto* ret = countTree.Find(e);if (ret == nullptr){countTree.Insert(e, 1);}else{ret->_value++;}}countTree.Inorder();
}
5、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
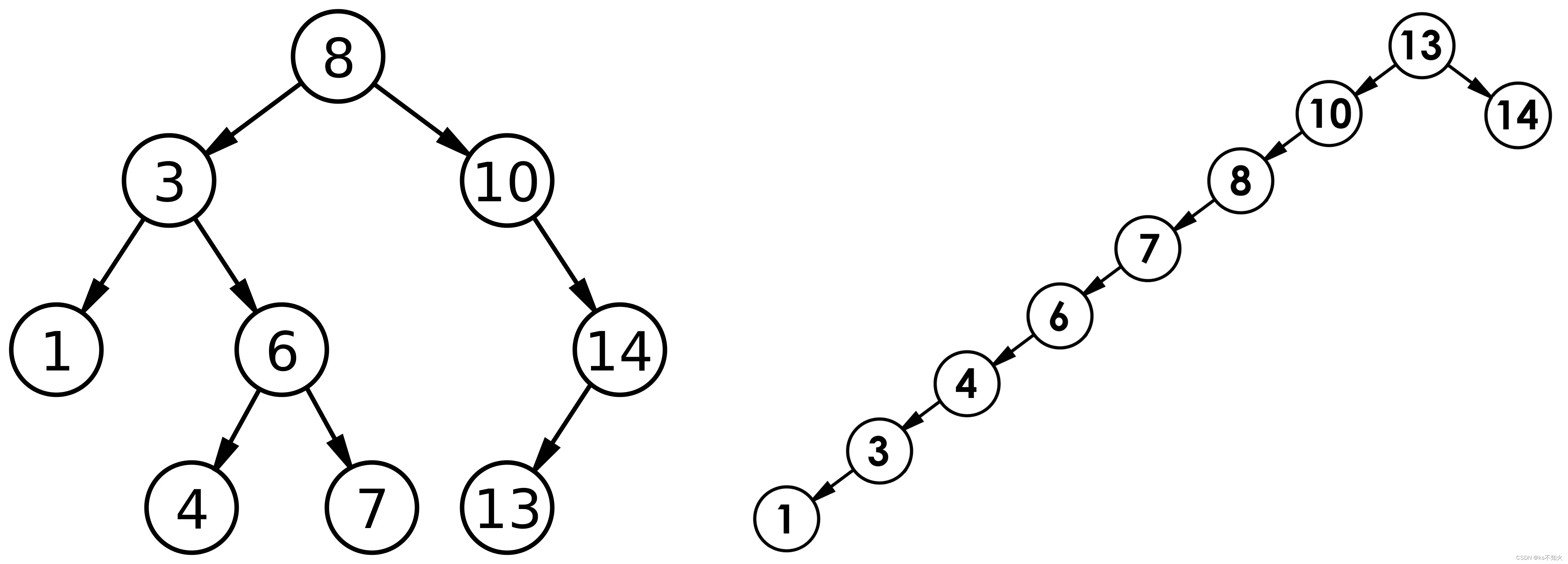
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log2Nlog_2 Nlog2N
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N2\frac{N}{2}2N
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插
入关键码,二叉搜索树的性能都能达到最优?那么我们后续章节学习的AVL树和红黑树就可以上
场了。
6、总结
二叉搜索树只是开胃小菜,主要就是为了下面的set和map、avl、红黑树等内容做铺垫。但是也要掌握,毕竟这是为了后面的内容打基础!
相关文章:

C++【二叉树进阶(二叉搜索树)】
文章目录前言1、二叉搜索树1-1、 二叉搜索树概念2、二叉搜索树操作2-1、树和节点的基本框架2-2、二叉搜索树的查找2-3、中序遍历2-4、二叉搜索树的插入2-5、二叉搜索树的删除3、二叉搜索树的模拟实现3-1、循环版本3-2、递归版本4、二叉搜索树的应用4-1、K模型4-2、KV模型4-3、K…...
【C++初阶】vector的使用
大家好我是沐曦希💕 文章目录一.vector介绍二、构造函数三、遍历1.[]2.迭代器3.范围for四、容量操作1.扩容机制五、增删查改六、迭代器失效问题一.vector介绍 vector是表示可变大小数组的序列容器。就像数组一样,vector也采用的连续存储空间来存储元素。…...

OPenPCDet windows流程及其问题
首先的首先极其不推荐将OPenPCDet运行在Windows上,过程非常复杂,适配也不是很好,不推荐在windows下载并训练,本人做这个主要是方便再笔记本电脑上对实验结果进行整理,处理一些简单的推理评估等任务。如有必要请继续阅读: 以下是正文: 常规的安装流程不再赘述,请参考官方…...

【自学Python】Python字符大小写判断
大纲 Python字符串是否是小写 Python字符串是否是小写教程 在开发过程中,有时候我们需要判断一个 字符串 是否是小写形式(即,所有的字符都是小写字母,不是英文字符的忽略不做判断),在 Python 中ÿ…...
设计模式之美总结(开源实战篇)
title: 设计模式之美总结(开源实战篇) date: 2023-01-10 17:13:05 tags: 设计模式 categories:设计模式 cover: https://cover.png feature: false 文章目录1. Java JDK 应用到的设计模式1.1 工厂模式在 Calendar 类中的应用1.2 建造者模式在 Calendar …...

两个月,测试转岗产品经理,我是怎么规划的?
本期同学依旧来自深圳 测试到产品转变,用了两个月 本周,为大家介绍M同学的佛系转岗经历 学员档 学员档案 原岗位:测试 转岗级别:中级产品经理 转岗特点: 1.未接触产品工作 2.对岗位地点要求严格 先看结果 …...
三数之和-力扣15-java排序+双指针
一、题目描述给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。注意:答案中不可以包含重复的三元组。…...
【编程基础之Python】3、创建Python虚拟环境
【编程基础之Python】3、创建Python虚拟环境创建Python虚拟环境为什么需要虚拟环境Windows上的Anaconda创建虚拟环境conda 命令conda env 命令创建虚拟环境切换虚拟环境验证虚拟环境Linux上的Anaconda创建虚拟环境创建虚拟环境切换虚拟环境验证虚拟环境总结创建Python虚拟环境 …...
kettle开发-Day36-循环驱动作业
前言:在日常数据处理时,我们通过变量传参来完成某个日期的数据转换。但可能因程序或者网络原因导致某个时间段的数据抽取失败。常见导致kettle作业失败的原因大概分为三大类,数据源异常、数据库异常、程序异常。因此面对这些异常时࿰…...

2023秋招 新凯来 算法工程师 面经分享
本专栏分享 计算机小伙伴秋招春招找工作的面试经验和面试的详情知识点 专栏首页:秋招算法类面经分享 主要分享计算机算法类在面试互联网公司时候一些真实的经验 一面 技术面 30分钟左右 1.主要是问项目和论文上的东西,问的不深,中间还介绍他们是做缺陷检测的,大概问了16分钟…...

Web3CN|Damus刷频背后,大众在期待什么样的去中心化社交?
刚过去的一周,许多人的朋友圈包括Twitter、Faceboo在内都在被一串公钥字母刷屏,其重要起因就是 Twitter 前首席执行官 Jack Dorsey 发推称,(2月1日)基于去中心化社交协议 Nostr 的社交产品 Damus 和 Amethyst 已分别在…...

Jenkins自动发布到WindowsServer,在WindowsServer执行的命令
echo off set apppoolname"6.usegitee" set websitename"6.usegitee" set webfolder"usegitee" echo 停止站点的应用程序池 C:\Windows\System32\inetsrv\appcmd.exe stop apppool %apppoolname% echo 停止站点 c:\Windows\System32\inetsrv\a…...
【Git学习】Git如何Clone带有Submodule的仓库?
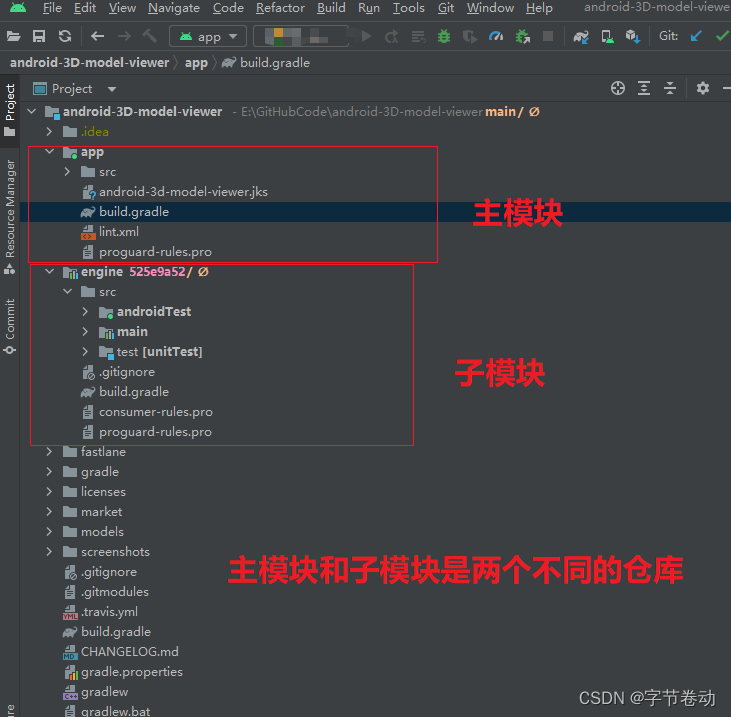
文章目录一、问题描述二、解决问题三、参考链接四、解决问题4.1 下载主模块4.2 查看主模块的配置4.2 子模块的添加4.3 查看子模块的配置4.4 查看子模块的检出状态4.5 检出submodule4.6 再次查看.git/config4.7 重新打开Android Studio运行代码一、问题描述 在GitHub上下载了一…...

C语言进阶——通讯录模拟实现
🌇个人主页:_麦麦_ 📚今日名言:只有走在路上,才能摆脱局限,摆脱执着,让所有的选择,探寻,猜测,想象都生机勃勃。——余秋雨《文化苦旅》 目录 一、前言 二、正…...

【C#基础】C# 变量和常量的使用
序号系列文章1【C#基础】C# 程序通用结构总结2【C#基础】C# 程序基础语法解析3【C#基础】C# 数据类型总结文章目录前言一. 变量(variable)1,变量定义及初始化2,变量的类别3,接收输出变量二. 常量(constant&…...
nvm安装后出现‘node‘ 不是内部或外部命令,也不是可运行的程序 或批处理文件
出现这个问题多半是path地址不对。 打开系统环境变量。看看path里面有没有?没有的话,加上就行! 我的报错原因就是因为path里没有自动加上nvm的相关路径。 注意项: 1,在安装nvm之前,提前要把本机以前安装…...

张驰咨询:关于六西格玛,有一些常见的疑惑!
很多想要学习六西格玛的学员,经常会有这些困惑: 以前没有接触过六西格玛,需要什么基础吗?自学还是培训?哪些行业会用到六西格玛呢?学习六西格玛对以后的工作有哪些帮助?如何选择六西格玛培…...
【Vercel】教你部署imsyy/home个人主页
本篇博客教你如何部署一个自己的个人主页 项目地址:https://github.com/imsyy/home 本文首发于 慕雪的寒舍 1.fork仓库vercel部署 首先我们点击fork,将仓库复刻到自己的账户 随后进入vercel,点击dashboard-add new-project 选择你复刻的仓库…...
GeekChallenge
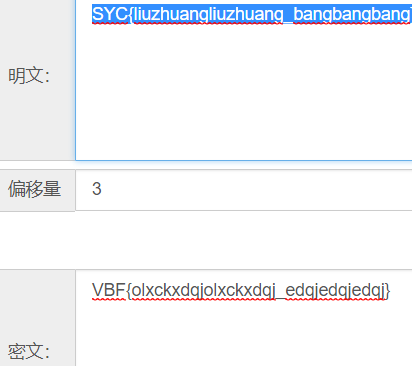
2.GeekChallenge 1.web 1.朋友的学妹 url:http://49.234.224.119:7413/ 右键点击查看源码,找到flagU1lDe0YxQF80c19oNExwZnVsbGxsbGx9 然后base64解码得到SYC{F1_4s_h4Lpfullllll} 2.EZwww url:http://47.100.46.169:3901/ 根据网站提示…...

Java文件IO
文章目录Java中的文件操作File常用构造方法方法文件内容的读写——数据流InputStreamFileInputStream利用Scanner进行字符读取OutputStreamPrintWriter按字符读取文件(FileReader)练习代码实例如何按字节进行数据读如何按字节进行数据写如何按字符进行数据读如何按字符进行数据…...

新手零基础入门:在快马平台动手实现第一个虚拟机监控界面
对于刚接触开发的新手来说,虚拟机监控听起来是个挺“高大上”的概念,涉及到服务器、后端数据采集、复杂图表库等等,光是想想配置环境就让人头大。但最近我在InsCode(快马)平台上尝试了一下,发现其实可以抛开那些复杂的后端和运维知…...

轻量级实战:利用 K3s 和 Kubeflow 构建高效 AI 开发环境
1. 为什么你需要一个轻量级的本地AI开发环境? 如果你正在学习机器学习,或者在一个小团队里捣鼓AI模型,我猜你肯定遇到过这样的烦恼:每次想跑个实验,要么得去申请云上的GPU实例,流程繁琐不说,成本…...

效率提升:用快马一键生成高性能数据处理模块,替换项目瓶颈
最近在做一个数据处理相关的项目,遇到了一个典型的性能瓶颈:一个处理大规模JSON数组的模块,随着数据量增长,执行时间越来越长,严重拖慢了整体流程。手动去优化这种底层逻辑,既要考虑算法效率,又…...

云端部署 OpenClaw 通过插件操作本机浏览器
前言:最近openclaw大火,网上的热度也是水涨船高,我的openclaw是部署到云服务器上,想让他操控我本地的电脑进行一些简单的网页操作,在网上搜索了相关资料,有了这篇教程,后续会分享更多开发实战干…...

告别VIP音频下载烦恼:xmly-downloader-qt5让你轻松获取喜马拉雅付费内容
告别VIP音频下载烦恼:xmly-downloader-qt5让你轻松获取喜马拉雅付费内容 【免费下载链接】xmly-downloader-qt5 喜马拉雅FM专辑下载器. 支持VIP与付费专辑. 使用GoQt5编写(Not Qt Binding). 项目地址: https://gitcode.com/gh_mirrors/xm/xmly-downloader-qt5 …...
实战:从CMOS传输门到零阈值元件设计避坑指南)
通路晶体管逻辑(PTL)实战:从CMOS传输门到零阈值元件设计避坑指南
通路晶体管逻辑(PTL)实战:从CMOS传输门到零阈值元件设计避坑指南 在数字电路设计的演进历程中,通路晶体管逻辑(PTL)以其独特的架构优势,持续为高性能、低功耗集成电路提供创新解决方案。不同于传统CMOS逻辑的全电压摆幅…...

NPYViewer:革新性NumPy数据可视化工具,让科学数据直观呈现
NPYViewer:革新性NumPy数据可视化工具,让科学数据直观呈现 【免费下载链接】NPYViewer Load and view .npy files containing 2D and 1D NumPy arrays. 项目地址: https://gitcode.com/gh_mirrors/np/NPYViewer 在数据驱动的科研与工程领域&#…...

ESP32端云协同语音助手:嵌入式AI交互系统设计与实现
1. 项目概述ESP32-AI语音助手是一个面向嵌入式边缘智能交互场景的软硬协同系统,其核心目标是将大语言模型(LLM)能力下沉至资源受限的MCU级平台,在不依赖手机或PC中转的前提下,实现端侧语音唤醒、语义理解、多模态响应与…...

地图应用性能调优实战:巧用 willReadFrequently 消除 Canvas2D 的 getImageData 性能警告
1. 地图应用中的Canvas2D性能警告从何而来? 最近在开发一个地图应用时,控制台突然频繁出现这样的警告:"Canvas2D: Multiple readback operations using getImageData are faster with the willReadFrequently attribute set to true&quo…...

Qwen-Image-2512基础教程:模型挂载路径规范、权限配置与持久化存储配置
Qwen-Image-2512基础教程:模型挂载路径规范、权限配置与持久化存储配置 想快速搭建一个能生成高质量像素艺术图片的AI服务吗?今天,我们就来手把手教你部署一个基于 Qwen-Image-2512 大模型和 Pixel Art LoRA 的专属像素艺术生成器。这个服务…...
