树链剖分(重链剖分)
树链剖分的核心思想就是将一棵树剖分成一条一条的链
因为树不好处理 但链比较好处理
为了学会它 我们先要学会树上dfs(深度优先搜索) 然后就没了(雾)
Because 树链剖分需要用到两个dfs
哦对了 我们还要了解以下的知识点
1.子树大小
就是一个节点的子树的节点个数(包括它自己)
2.重儿子
一个节点的所有儿子中子树大小最大的儿子
3.轻儿子
除了重儿子之外的儿子(包括根节点)
4.重边
两个相邻的重儿子连成的边
5.重链
重边连成的链(开头是轻儿子)
OK,了解完了
启动!
dfs1:
目标是求出以下数据
1: 节点的父节点
2: 节点的深度 也就是它到根节点的距离
3: 节点的重儿子
4: 节点的子树大小
思路十分的简单 直接上代码
void dfs1(int x)
{deep[x]=deep[fa[x]]+1;si[x]=1;//它自己也是 for(int i=0;i<a[x].size();i++){if(a[x][i]==fa[x]) continue;fa[a[x][i]]=x;dfs1(a[x][i]);si[x]+=si[a[x][i]];if(si[a[x][i]]>si[son[x]]) son[x]=a[x][i];}
}dfs2:
目标是求出以下数据
1: 节点的所在的重链的顶端节点
2: 节点的新编号
3: 节点的新编号的值
其中 新编号的原则是先走重儿子 再走轻儿子(理由下次一定)
比如

懂了吗? 我相信你肯定懂了
思路也十分的简单 直接上代码
void dfs2(int x,int topf)
{id[x]=++cnt;top[x]=topf;b[cnt]=w[x];if(!son[x]) return;dfs2(son[x],topf);for(int i=0;i<a[x].size();i++){if(a[x][i]==fa[x]||a[x][i]==son[x]){continue;}dfs2(a[x][i],a[x][i]);}
}我们发现先走重儿子的话 就可以让重链上的点的新编号是连续的 也就形成了一条链
至此 树链剖分就结束了
那你一定很想问 这玩意有什么用呢?
题目
我们结合题目来看(其实是模板)
前置芝士:线段树
让我们处理4种操作
我们先来看操作3和操作4
通过观察图片可以看出

一个节点的子树的编号肯定是连续的
设子树的根是
左端点是的编号是 右端点的编号是
所以3操作就是将到
加上
4操作就是求出到
的值的和
即区间修改 ,区间查询
我们当然会想到线段树啦
直接拿下
之后我们来看1,2操作
先来看一看图

比如我们要从 7 到 4
我们可以先判断它俩的top是不是一个东西 发现不是
发现4的深度比7小 这怎么可以呢?
我们交换一下 变成从 4 到 7
然后把4跳到它的top的父节点
也就是0(1的父节点是0)
并加上 1 到 4 的值 可以用线段树处理
之后在循环上述操作
直到两者的top相等
上代码
int getsum1(int x,int y)
{int sum=0;while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]]){swap(x,y);}sum=sum+query(1,1,n,id[top[x]],id[x]);x=fa[top[x]];}if(deep[x]>deep[y]){swap(x,y);}sum+=query(1,1,n,id[x],id[y]);return sum;
}修改也差不多 直接上代码
void addsum1(int x,int y,int z)
{while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]]){swap(x,y);}add(1,1,n,id[top[x]],id[x],z);x=fa[top[x]];}if(deep[x]>deep[y]){swap(x,y);}add(1,1,n,id[x],id[y],z);
}完整版:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,cnt,m,r,mod;
int b[110000],top[110000],w[110000],deep[110000],id[110000],fa[110000],si[110000],son[110000],tr[410000],tag[410000];
vector<int>a[110000];
void dfs1(int x)
{deep[x]=deep[fa[x]]+1;si[x]=1;//它自己也是 for(int i=0;i<a[x].size();i++){if(a[x][i]==fa[x]) continue;fa[a[x][i]]=x;dfs1(a[x][i]);si[x]+=si[a[x][i]];if(si[a[x][i]]>si[son[x]]) son[x]=a[x][i];}
}
void dfs2(int x,int topf)
{id[x]=++cnt;top[x]=topf;b[cnt]=w[x];if(!son[x]) return;dfs2(son[x],topf);for(int i=0;i<a[x].size();i++){if(a[x][i]==fa[x]||a[x][i]==son[x]){continue;}dfs2(a[x][i],a[x][i]);}
}
void build(int k,int l,int r)
{if(l==r){tr[k]=b[l];return;}int mid=(l+r)>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);tr[k]=tr[k<<1]+tr[k<<1|1];
}
void push_down(int k,int l,int r)
{if(tag[k]){int mid=(l+r)>>1;tag[k<<1]+=tag[k];tag[k<<1|1]+=tag[k];tr[k<<1]+=(mid-l+1)*tag[k];tr[k<<1|1]+=(r-mid)*tag[k];tag[k]=0;}
}
void add(int k,int l,int r,int q,int p,int d)
{if(q<=l&&p>=r){tag[k]+=d;tr[k]+=(r-l+1)*d;return;}push_down(k,l,r);int mid=(l+r)>>1;if(mid>=q){add(k<<1,l,mid,q,p,d);}if(mid<p){add(k<<1|1,mid+1,r,q,p,d);}tr[k]=(tr[k<<1]+tr[k<<1|1]);
}
int query(int k,int l,int r,int q,int p)
{if(q<=l&&p>=r){return tr[k];}push_down(k,l,r);int mid=(l+r)>>1,ssum=0;if(mid>=q){ssum+=query(k<<1,l,mid,q,p);}if(mid<p){ssum+=query(k<<1|1,mid+1,r,q,p);}return ssum;
}
int getsum1(int x,int y)
{int sum=0;while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]]){swap(x,y);}sum=sum+query(1,1,n,id[top[x]],id[x]);x=fa[top[x]];}if(deep[x]>deep[y]){swap(x,y);}sum+=query(1,1,n,id[x],id[y]);return sum;
}
int getsum2(int x)
{return query(1,1,n,id[x],id[x]+si[x]-1);
}
void addsum1(int x,int y,int z)
{while(top[x]!=top[y]){if(deep[top[x]]<deep[top[y]]){swap(x,y);}add(1,1,n,id[top[x]],id[x],z);x=fa[top[x]];}if(deep[x]>deep[y]){swap(x,y);}add(1,1,n,id[x],id[y],z);
}
void addsum2(int x,int y)
{add(1,1,n,id[x],id[x]+si[x]-1,y);
}
signed main()
{scanf("%lld%lld%lld%lld",&n,&m,&r,&mod);for(int i=1;i<=n;i++){scanf("%lld",&w[i]);}for(int i=1;i<n;i++){int x,y;scanf("%lld%lld",&x,&y);a[x].push_back(y);a[y].push_back(x);}dfs1(r);dfs2(r,r);build(1,1,n);while(m--){int op;scanf("%lld",&op);if(op==1){int x,y,z;scanf("%lld%lld%lld",&x,&y,&z);addsum1(x,y,z);}if(op==2){int x,y;scanf("%lld%lld",&x,&y);printf("%lld\n",getsum1(x,y)%mod);}if(op==3){int x,y;scanf("%lld%lld",&x,&y);addsum2(x,y);}if(op==4){int x;scanf("%lld",&x);printf("%lld\n",getsum2(x)%mod);}}return 0;
}相关文章:

树链剖分(重链剖分)
树链剖分的核心思想就是将一棵树剖分成一条一条的链 因为树不好处理 但链比较好处理 为了学会它 我们先要学会树上dfs(深度优先搜索) 然后就没了(雾) Because 树链剖分需要用到两个dfs 哦对了 我们还要了解以下的知识点 1.子…...

幻读是什么?用什么隔离级别可以防止幻读?
幻读是什么? 幻读(Phantom Read) 是数据库事务中的一种现象,指的是在一个事务中,当执行两次相同的查询时,第二次查询返回的结果集包含了第一次查询中不存在的行,或者第一次查询中存在的行在第二…...

[Unity Demo]从零开始制作空洞骑士Hollow Knight第二十集:制作专门渲染HUD的相机HUD Camera和画布HUD Canvas
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、制作HUD Camera以及让两个相机同时渲染屏幕二、制作HUD Canvas 1.制作法力条Soul Orb引入库2.制作生命条Health读入数据3.制作吉欧统计数Geo Counter4.制作…...
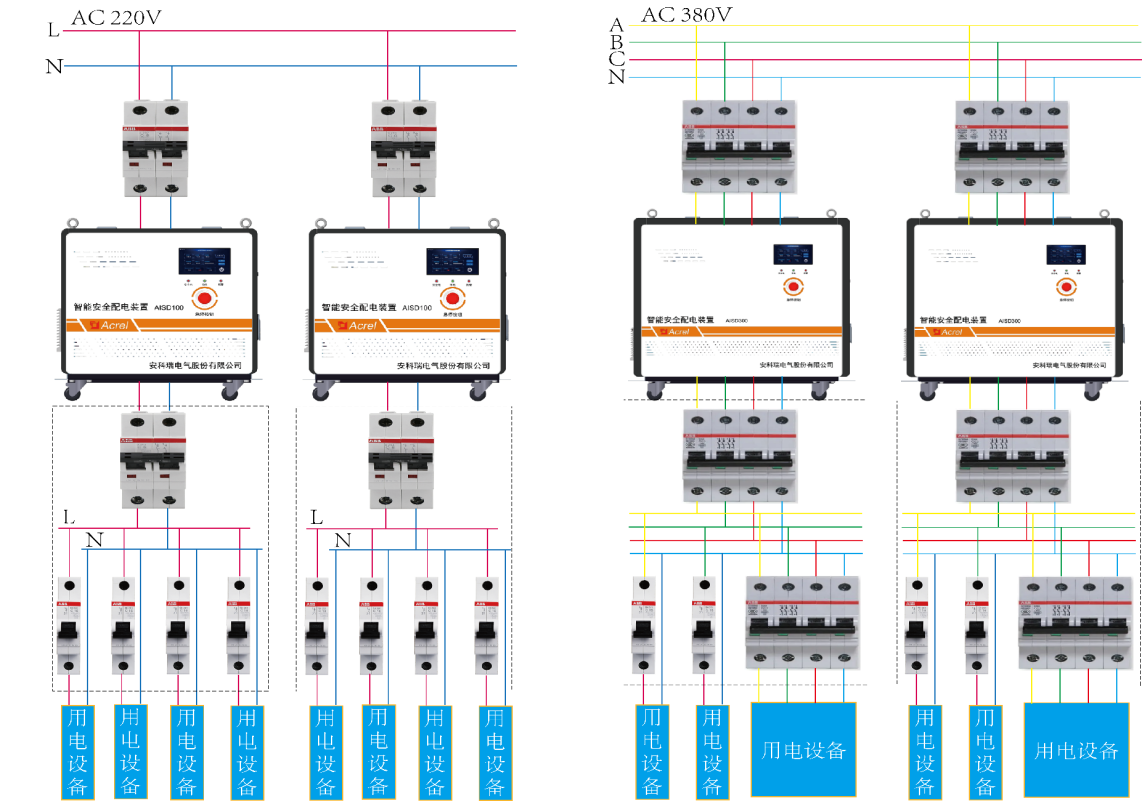
智能安全配电装置在高校实验室中的应用
摘要:高校实验室是科研人员进行科学研究和实验的场所,通常会涉及到大量的仪器设备和电气设备。电气设备的使用不当或者维护不周可能会引发火灾事故。本文将以一起实验室电气火灾事故为例,对事故原因、危害程度以及防范措施进行分析和总结…...
)
网络安全等级保护测评机构管理办法(全文)
网络安全等级保护测评机构管理办法(公信安〔2018〕765号) 第一章 总则 第一条 为加强网络安全等级保护测评机构(以下简称“测评机构”)管理,规范测评行为,提高等级测评能力和服务水平,根据《中华人民共和国网络安全法…...

Flutter:shared_preferences数据存储,数据持久化,token等信息存储
官方示例:简单调用 // 初始化示例 final SharedPreferences prefs await SharedPreferences.getInstance(); // 存int await prefs.setInt(counter, 10); // 存bool await prefs.setBool(repeat, true); // 存double await prefs.setDouble(decimal, 1.5); // 存st…...

FileProvider高版本使用,跨进程传输文件
高版本的android对文件权限的管控抓的很严格,理论上两个应用之间的文件传递现在都应该是用FileProvider去实现,这篇博客来一起了解下它的实现原理。 首先我们要明确一点,FileProvider就是一个ContentProvider,所以需要在AndroidManifest.xml里面对它进行声明: <provideran…...

python学习记录18
1 函数的定义 python中的函数指使用某个定义好的名字指代一段完整的代码,在使用名字时可以直接调用整个代码,这个名字叫做函数名。利用函数可以达到编写一次即可多次调用的操作,从而减少代码量。 函数分为内置函数与自定义函数。内置函数例…...

云原生之k8s服务管理
文章目录 服务管理Service服务原理ClusterIP服务 对外发布应用服务类型NodePort服务Ingress安装配置Ingress规则 Dashboard概述 认证和授权ServiceAccount用户概述创建ServiceAccount 权限管理角色与授权 服务管理 Service 服务原理 容器化带来的问题 自动调度:…...

redis工程实战介绍(含面试题)
文章目录 redis单线程VS多线程面试题**redis是多线程还是单线程,为什么是单线程****聊聊redis的多线程特性和IO多路复用****io多路复用模型****redis如此快的原因** BigKey大批量插入数据测试数据key面试题海量数据里查询某一固定前缀的key如果生产上限值keys * ,fl…...

再次讨论下孤注一掷
在孤注一掷中的黑客技术里面,简单介绍了电影孤注一掷中用的一些"黑科技",这里继续讨论下,抛弃这些黑科技,即使在绝对公平的情况下,你也一样赢不了赌场 相对论有一个假设就是光速不变,这里也有个…...

LeetCode46.全排列
LeetCode刷题记录 文章目录 📜题目描述💡解题思路⌨C代码 📜题目描述 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例1 输入:nums [1,2,3] 输出:[[1,2,…...

蓝桥杯-洛谷刷题-day4(C++)
目录 1.高精度乘法 i.P1303 A*B Problem高精度乘法 2.P4924 [1007] 魔法少女小Scarlet i.题目 ii.代码 3.二维数组 i.二维数组的建立 ii.备份 iii.二维数组的转动 4.指令的及时处理 1.高精度乘法 即,将每一位变为数组中的一位,并在数组中以倒序排列&a…...

c++总复习
1. C 中的移动语义及其作用 定义 移动语义是 C 11 引入的一种重要特性,它用于优化对象的资源管理,特别是在涉及对象所有权转移的场景中。传统的 C 语义在对象赋值或传递给函数时,通常会进行拷贝操作,即创建源对象的一个完整副本&…...

设计模式之策略模式-工作实战总结与实现
文章目录 应用场景存在问题解决方案继续延伸 应用场景 假设有这样的业务场景,大数据系统把文件推送过来,根据不同类型采取不同的解析方式。多数的小伙伴就会写出以下的代码: public class Question {public static void main(String[] args…...

E - 11/22 Subsequence题解
文章目录 大致思路代码 大致思路 预处理: 用pos1, pos2, posls 分别记录 1 1 1, 2 2 2 , / / / 在字符串中的『位置』 用cum1 和 cum2 分别存储了 1 1 1 和 2 2 2 的前缀和,这样可以快速获取任意区间内的 1 1 1 和 2 2 2 的『数量』 查询处理: 对于每个查询…...
PyPI 攻击:ChatGPT、Claude 模仿者通过 Python 库传播 JarkaStealer
《Java代码审计》http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247484219&idx1&sn73564e316a4c9794019f15dd6b3ba9f6&chksmc0e47a67f793f371e9f6a4fbc06e7929cb1480b7320fae34c32563307df3a28aca49d1a4addd&scene21#wechat_redirect 《Web安全》h…...

单片机学习笔记 9. 8×8LED点阵屏
更多单片机学习笔记:单片机学习笔记 1. 点亮一个LED灯单片机学习笔记 2. LED灯闪烁单片机学习笔记 3. LED灯流水灯单片机学习笔记 4. 蜂鸣器滴~滴~滴~单片机学习笔记 5. 数码管静态显示单片机学习笔记 6. 数码管动态显示单片机学习笔记 7. 独立键盘单片机学习笔记 8…...

【大模型-智能体】AutoGen Studio测试和导出工作流程
1. 测试工作流程 AutoGen Studio允许用户针对任务交互式地测试工作流程,并审查由此产生的成果物(如图像、代码和文档)。此外用户还可以查看Agent工作流程在处理任务时的“内心独白”,并查看诸如运行成本(如回合数、令牌…...

【Linux】-学习笔记04
第十二章、磁盘管理 1.查看磁盘空间使用量 1.1df命令 作用: 列出文件系统的磁盘空间占用情况 df,disk free,通过文件系统来快速获取空间大小的信息,当我们删除一个文件的时候,这个文件 不是马上就在文件系统当中消…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
