线性代数在人工智能领域中的实践
一、机器学习中的线性代数应用
在机器学习中,线性代数主要用于构建和训练各种模型,如线性回归、逻辑回归、支持向量机等。这些模型在数据的特征提取、降维处理以及分类等方面发挥了重要作用。
- 线性回归:线性回归是最简单的机器学习算法之一,它基于线性关系对数据进行预测。在线性回归中,输入特征和目标变量之间的关系可以用一个线性方程来表示,这个方程的参数可以通过最小二乘法来求解。线性方程的参数可以看作是一个向量,而输入特征可以看作是一个矩阵,通过矩阵运算可以求出预测值。
- 逻辑回归:逻辑回归是一种用于分类的算法,它通过将线性回归的输出映射到0和1之间,从而实现对二分类问题的处理。逻辑回归中的参数求解同样需要用到线性代数的知识,如向量的内积和矩阵的乘法等。
- 支持向量机(SVM):SVM是一种基于最大间隔分类思想的算法,它通过找到一个超平面将不同类别的数据分开。在SVM中,需要用到向量的内积和范数等线性代数的知识来计算数据点到超平面的距离,从而确定分类结果。

此外,线性代数也是构建神经网络的重要基础。在深度学习中,矩阵运算和线性变换是处理复杂数据的关键步骤。神经网络中的权重和偏置都是矩阵或向量,神经网络的前向传播和反向传播都是基于矩阵乘法和向量运算的。例如,在卷积神经网络(CNN)中,卷积操作本质上就是一个线性变换,它利用卷积核对图像进行卷积运算,从而提取图像的特征。
二、图像处理中的线性代数应用
在图像处理中,线性代数的方法被广泛应用于图像的变换、滤波、压缩以及三维重建等方面。
- 图像的变换:通过线性代数中的矩阵乘法,可以将图像从一个坐标系转换到另一个坐标系,或者将图像从一个颜色空间转换到另一个颜色空间。例如,通过傅里叶变换可以将图像从空间域转换到频率域,从而实现图像的滤波和降噪。
- 图像的滤波:在图像处理中,滤波是一种常见的操作,它可以通过线性代数中的矩阵运算来实现。例如,高斯滤波器就是一种基于线性代数的滤波方法,它利用高斯函数对图像进行平滑处理,从而去除噪声和细节。
- 图像的压缩:在图像压缩中,常常使用矩阵分解技术来减少图像数据的大小。例如,奇异值分解(SVD)就是一种常用的矩阵分解方法,它可以将一个矩阵分解为两个较小的矩阵的乘积,从而实现对图像的压缩。
三、自然语言处理中的线性代数应用
在自然语言处理中,线性代数的方法也被广泛应用。例如,词向量表示(word embeddings)就是利用线性代数的方法将词语或句子转换为固定维度的向量,以便于进行机器学习和数据分析。
- 词向量表示:词向量表示是一种将词语转换为向量的方法,它可以通过线性代数中的矩阵运算来实现。例如,Word2Vec就是一种常用的词向量表示方法,它利用神经网络的训练过程将词语映射到一个高维向量空间中,从而实现对词语的语义表示。
- 文本分类:在文本分类中,可以利用线性代数中的向量空间运算来进行分类。例如,可以使用支持向量机(SVM)或K近邻算法(KNN)等分类器对文本进行分类,这些分类器都需要用到向量的内积和距离等线性代数的知识。
- 情感分析:在情感分析中,可以利用线性代数中的向量空间运算来进行情感分析。例如,可以使用主题模型(LDA)或情感词典等方法对文本进行情感分析,这些方法都需要用到向量的表示和运算。
四、数据挖掘中的线性代数应用
在线性代数中,数据的降维处理是数据挖掘的重要步骤之一。通过将高维数据转换为低维数据,可以更好地理解和分析数据的内在结构和模式。
- 主成分分析(PCA):PCA是一种常用的数据降维方法,它利用线性代数的理论和方法对数据进行特征值分解,从而得到数据的主成分。通过保留主成分,可以实现对数据的降维处理,同时保留数据的主要信息。
- 奇异值分解(SVD):SVD是一种常用的矩阵分解方法,它可以将一个矩阵分解为两个较小的矩阵的乘积。在数据挖掘中,SVD可以用于数据的降维和压缩等任务。
五、优化问题中的线性代数应用
在人工智能中,许多问题都可以转化为优化问题,如路径规划、决策理论等。而线性代数是解决这些优化问题的重要工具之一。
- 线性规划:线性规划是一种求解线性目标函数在线性约束条件下的最优解的方法。通过线性代数的理论和方法,可以求解线性规划问题,从而得到最优解。
- 非线性规划:非线性规划是一种求解非线性目标函数在非线性约束条件下的最优解的方法。虽然非线性规划问题比线性规划问题更复杂,但也可以利用线性代数的理论和方法进行求解。例如,可以利用梯度下降算法等优化算法来求解非线性规划问题。
六、强化学习中的线性代数应用
在强化学习中,智能体通过与环境的交互不断学习和改进自己的策略。在这个过程中,线性代数的方法被用来处理状态转移矩阵和奖励函数等信息,帮助智能体更好地理解环境并做出最优决策。
- 状态转移矩阵:在强化学习中,状态转移矩阵描述了智能体在不同状态之间的转移概率。通过线性代数的理论和方法,可以计算状态转移矩阵的特征值和特征向量等属性,从而分析智能体的行为模式和策略。
- 奖励函数:奖励函数是强化学习中的一个重要组成部分,它描述了智能体在采取不同行动时所获得的奖励值。通过线性代数的理论和方法,可以计算奖励函数的期望值和方差等统计量,从而评估智能体的性能和策略。
相关文章:

线性代数在人工智能领域中的实践
一、机器学习中的线性代数应用 在机器学习中,线性代数主要用于构建和训练各种模型,如线性回归、逻辑回归、支持向量机等。这些模型在数据的特征提取、降维处理以及分类等方面发挥了重要作用。 线性回归:线性回归是最简单的机器学习算法之一…...

图片生成视频-右进
右侧进入 ffmpeg -loop 1 -i image.jpg -f lavfi -i colorcblack:s1280x720:d20 -filter_complex "[1:v]formatrgba[bg];[0:v]formatrgba,scale1280:720[img];[bg][img]overlayxif(lt(t,3),W,if(lt(t,8),W-(t-3)*W/5,0)):y(H-h)/2:enablegte(t,3)" -c:v libx264 -t 2…...

3、集线器、交换机、路由器、ip的关系。
集线器、交换机、路由器三者的关系 1、集线器2、交换机(每个交换机是不同的广播域,ip地址起到划分广播域的作用)3、 路由器4、ip地址 所有图片和资料均来源于B站:网络安全收藏家 1、集线器 一开始两台电脑通信就需要网线就可以&a…...

w~视觉~合集25
我自己的原文哦~ https://blog.51cto.com/whaosoft/12627822 #Mean Shift 简单的介绍 Mean Shift 的数学原理和代码实现,基于均值漂移法 Mean Shift 的图像分割 Mean Shift 算法简介 从分割到聚类 对于图像分割算法,一个视角就是将图像中的某些点集分为一类&a…...

Applicaiton配置文件
server:port: 8080 # 配置 Spring Boot 启动端口,默认为 8080mybatis-plus:mapper-locations: classpath:com/xtl/mapper/xml/*.xml # 指定 MyBatis Mapper XML 文件的路径,确保 MyBatis 能够正确加载 Mapper 文件global-config:db-config:id-type: au…...

(已解决)wps无法加载此加载项程序mathpage.wll
今天,在安装Mathtype的时候遇到了点问题,如图所示 尝试了网上的方法,将C:\Users\Liai_\AppData\Roaming\Microsoft\Word\STARTUP路径中的替换为32位的Mathtype加载项。但此时,word又出现了问题 后来知道了,这是因为64位…...

ubity3D基础
Unity是一个流行的游戏开发引擎,它使用C#作为其主要的编程语言。以下是一些Unity中C#编程的基础概念: • Unity编辑器: • Unity编辑器是Unity游戏引擎的核心,提供了一个可视化界面,用于创建和管理游戏项目。 • C#脚本…...

Python2和Python3的区别
和python 2.x相比,python 3.x版本在语句输出、编码、运算和异常等方面做出了一些调整,我们这篇文章就对这些调整做一个简单的介绍。 Python3.x print函数代替了print语句 在python 2.x中,输出数据使用的是print语句,例如ÿ…...

Spring框架整合单元测试
目录 一、配置文件方式 1.导入依赖 2.编写类和方法 3.配置文件applicationContext-test.xml 4.测试类 5.运行结果 二、全注解方式 1.编写类和方法 2.配置类 3.测试类 4.运行结果 每次进行单元测试的时候,都需要编写创建工厂,加载配置文件等相关…...

docker-mysql
一、创建mysql 1、docker run --name mysql8.0-container -e MYSQL_ROOT_PASSWORDmy-secret-pw -d -p 3306:3306 mysql:8.0 参数解释: --name mysql8.0-container:指定容器的名称为mysql8.0-container。 -e MYSQL_ROOT_PASSWORDmy-secret-pw:…...

Java程序基础⑤Java数组的定义和使用+引用的概念
目录 1. Java数组的基本概念 1.1 数组的定义 1.2 数组存在的意义 1.3 数组的使用 1.4 二维数组 2. 引用类型JVM的内存分布 2.1 JVM的内存分布 2.2 基本数据类型和引用型数据类型的区别 2.3 引用注意事项 2.4 传值传递 3. 数组总结和应用场景 3.1 一维数组和二维数组…...

electron主进程和渲染进程之间的通信
主进程 (main.js) const { app, BrowserWindow, ipcMain } require("electron"); const path require("node:path"); // 导入fs模块 const fs require("fs");const createWindow () > {const win new BrowserWindow({width: 800,height…...

uniapp 安卓和ios震动方法,支持息屏和后台震动,ios和安卓均通过测试
最近使用uniapp开发震动功能,发现uniapp提供的 uni.vibrateLong()的方法震动比较弱,而且不支持息屏和后台震动。plus.ios.importClass("UIImpactFeedbackGenerator")是在网上看到的,这个震动也比较弱,ios也不支持息屏和…...

# DBeaver 连接hive数仓
前提 前提是基于hadoop的hive服务已经启动,其中hive的服务包括metastore元数据服务和hiveserver2服务已经启动。hiveserver2服务在默认端口10000启动,且通过telnet xx.xx.xx.xx 10000 能通。 满足以上要求后,再可以看以下连接文档ÿ…...
STM32H7开发笔记(2)——H7外设之多路定时器中断
STM32H7开发笔记(2)——H7外设之多路定时器中断 文章目录 STM32H7开发笔记(2)——H7外设之多路定时器中断0.引言1.CubeMX配置2.软件编写 0.引言 本文PC端采用Win11STM32CubeMX4.1.0.0Keil5.24.2的配置,硬件使用STM32H…...
)
Pytorch使用手册-Build the Neural Network(专题五)
在 PyTorch 中如何构建一个用于 FashionMNIST 数据集分类的神经网络模型,并解析了 PyTorch 的核心模块 torch.nn 的使用方法。以下是具体内容的讲解: 构建神经网络 在 PyTorch 中,神经网络的核心在于 torch.nn 模块,它提供了构建神经网络所需的所有工具。关键点如下: nn.…...

16. Springboot集成Tika实现文档解析
目录 1、什么是Tika 2、基本特性 3、Tika可视化提取 4、Springboot集成 4.1、maven依赖 4.2、Tika配置文件 4.3、注入tika bean 4.4、Service类 4.5、测试类TikaParserDemoTest 1、什么是Tika Tika是一款Apache开源的,跨平台,支持多品种文本类…...

【单片机毕业设计12-基于stm32c8t6的智能称重系统设计】
【单片机毕业设计12-基于stm32c8t6的智能称重系统设计】 前言一、功能介绍二、硬件部分三、软件部分总结 前言 🔥这里是小殷学长,单片机毕业设计篇12-基于stm32c8t6的智能称重系统设计 🧿创作不易,拒绝白嫖可私 一、功能介绍 ----…...

[网络]无线通信中的AMPDU
定义 AMPDU(Aggregate MAC Protocol Data Unit)即聚合MAC协议数据单元。在无线通信中,特别是在IEEE 802.11n及后续的Wi - Fi标准(如802.11ac、802.11ax)中,它是一种用于提高数据传输效率的技术。简单来说&a…...
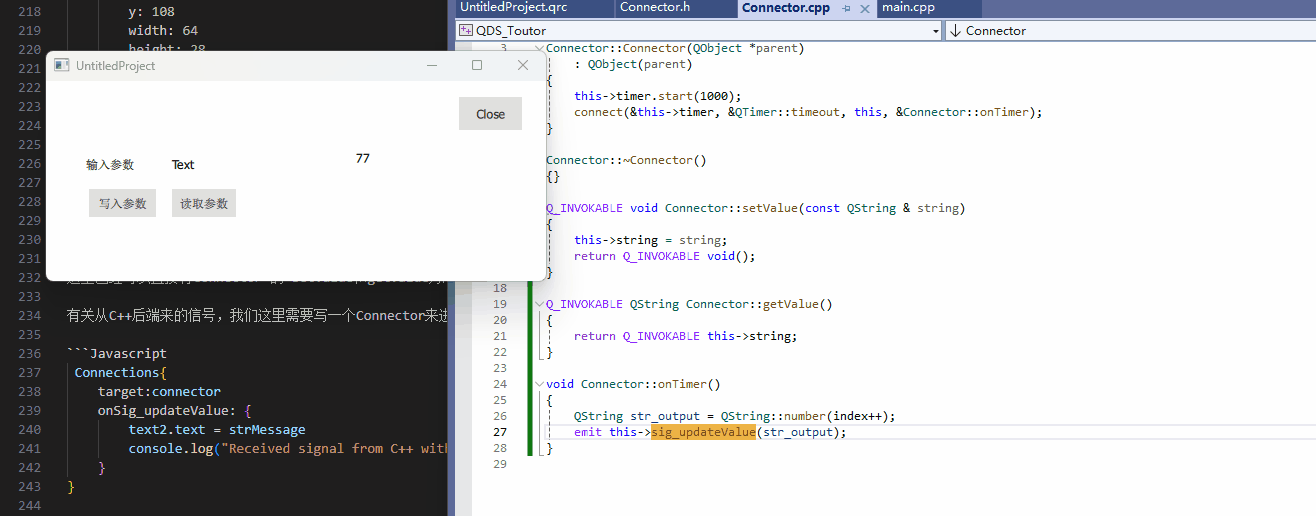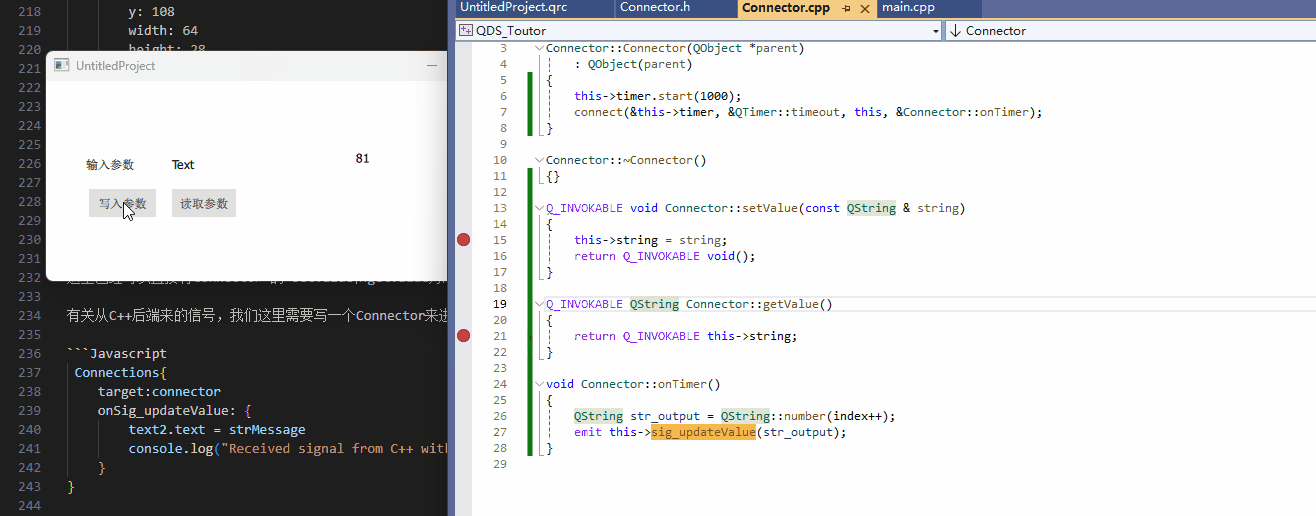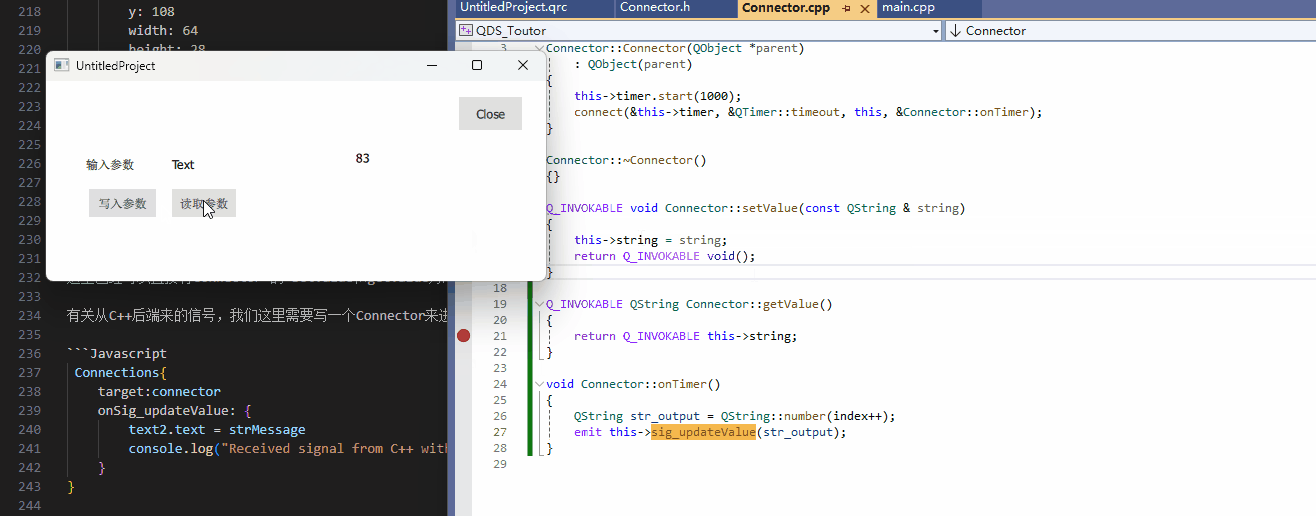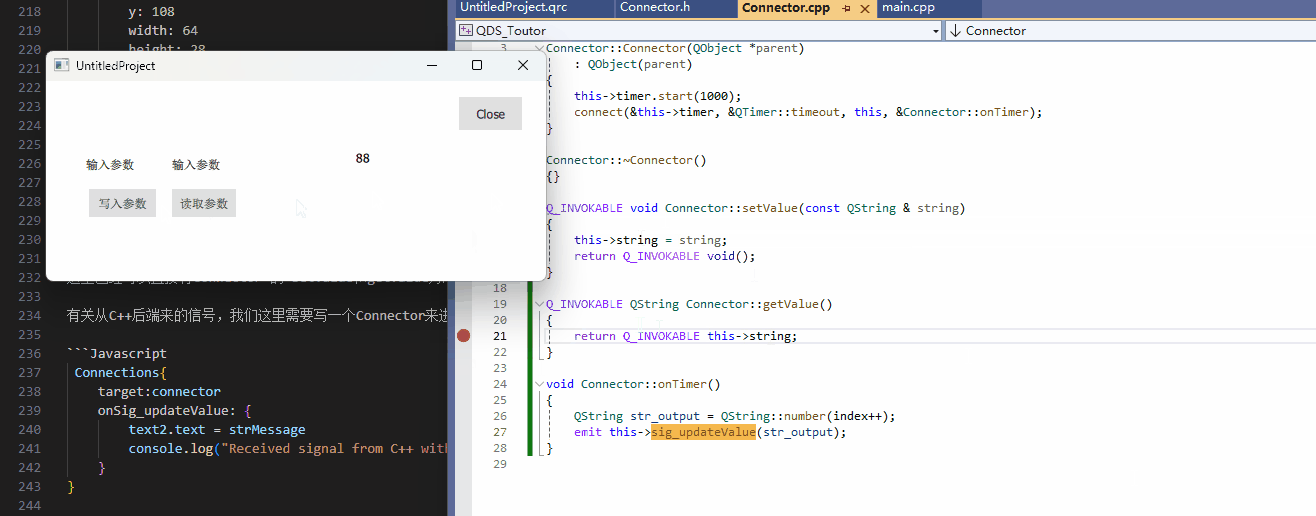
[QDS]从零开始,写第一个Qt Design Studio到程序调用的项目
前言 最近在使用Qt Design Studio进行开发,但是简中网上要不就是只搜得到Qt Designer(Qt Creator内部库),要不就只搜得到一点营销号不知道从哪里搬来的账号,鉴于Qt Design Studio是一个这么强大的软件,自然是需要来进行一下小小的…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
