什么是聚簇索引、非聚簇索引、回表查询
其实聚集索引也叫聚簇索引,二级索引也叫非聚簇索引,大家不要认为这是不同的两个知识点。
定义
先看一下数据库的索引介绍。
聚簇索引
1. 如果存在主键(一般都存在),主键索引就是聚簇索引。
2. 如果不存在,就用唯一索引(UNIQUE)做聚簇索引。
3. 如果表没有主键,也没有合适的唯一索引,则InnoDB会自动生成一个rowid作为隐藏的聚簇索引。
总而言之,一张表肯定是存在一个聚簇索引的 ,并且只能有一个,非叶子节点存储索引,叶子节点存储行数据。
假设一张表叫user,有如下三个字段

下面就是聚簇索引的结构图。

非聚簇索引
非聚簇索引存储的内容是主键,所以,我们根据非聚簇索引查询数据的时候,底层是可能会查两次的,这里我们给name字段加上非聚簇索引。
查两次情况: 执行select * from user where name = ’kit‘。
第一次: 根据非聚簇索引‘kit’查到对应数据的主键
第二次: 根据主键,也就是聚簇索引查询对应的行数据返回
查一次情况: 执行select id from user where name = 'kit'
第一次: 根据非聚簇索引‘kit’查到对应数据的主键,直接返回。

可能文字有些难以理解,现在根据上面两张图片和下面一张图片来看个例子,表名为‘user’,这里id是主键,自然对应聚簇索引,如果我们根据id 查询数据,例如select * from user where id = 5; 此时就会在聚簇索引中查询这一行数据直接返回。 现在我们给name加个非聚簇索引,现在根据name查询数据,select * from user where name = ”kit“,此时会根据非聚簇索引name查到对应的id为5,再根据id聚簇索引查询行数据返回。

回表查询
其实你已经见过回表查询了,你先看看概念,
回表查询是数据库中常见的一个概念,指的是当数据库引擎无法直接从索引中获取所需数据,而需要回到原始数据表中进行额外的查找操作。这种情况通常发生在查询语句中包含了索引无法覆盖的字段或者涉及到了复杂的查询条件时。回表查询会对数据库的性能产生不利影响,因为它需要更多的IO操作和数据扫描,导致查询速度变慢。
再看看非聚集索引的需要查两次的情况,这就是回表查询,回表查询查一次是不够的,要查多张表。
相关文章:

什么是聚簇索引、非聚簇索引、回表查询
其实聚集索引也叫聚簇索引,二级索引也叫非聚簇索引,大家不要认为这是不同的两个知识点。 定义 先看一下数据库的索引介绍。 聚簇索引 1. 如果存在主键(一般都存在),主键索引就是聚簇索引。 2. 如果不存在,…...

探索 Spring 框架核心组件:构建强大 Java 应用的基石
Spring框架作为Java企业级开发的首选框架之一,其强大的功能和灵活的架构深受开发者喜爱。Spring框架的核心组件共同构建了一个高效、可扩展的应用程序开发平台。本文将深入探讨Spring框架的核心组件,揭示它们如何在Spring框架中发挥关键作用。 一、Bean…...

Android 13 Aosp 默认允许应用动态权限
图库 frameworks/base/services/core/java/com/android/server/pm/permission/DefaultPermissionGrantPolicy.java 修改 public void grantDefaultPermissions(int userId) {DelayingPackageManagerCache pm new DelayingPackageManagerCache();grantPermissionsToSysCompon…...

【C++知识总结1】c++第一篇,简单了解一下命名空间是什么
一、C的由来 C语言是一种结构化和模块化的编程语言,它对于处理较小规模的程序非常适用。然而,当面临需要高度抽象和建模的复杂问题,以及规模较大的程序时,C语言就显得不那么合适了。为了应对这种挑战,并在解决软件危机…...

从0开始深度学习(32)——循环神经网络的从零开始实现
本章将从零开始,基于循环神经网络实现字符级语言模型(不是单词级) 首先我们把从0开始深度学习(30)——语言模型和数据集中的load_corpus_time_machine()函数进行引用,用于导入数据: train_iter…...
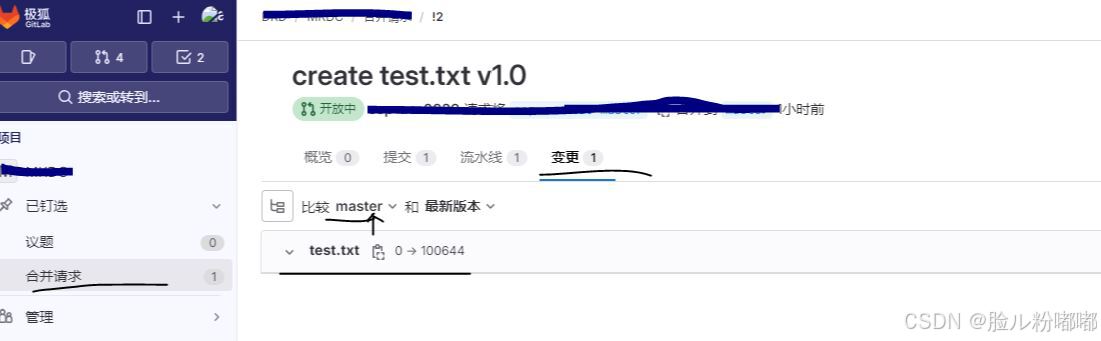
GitLab使用操作v1.0
1.前置条件 Gitlab 项目地址:http://******/req Gitlab账户信息:例如 001/******自己的分支名称:例如 001-master(注:master只有项目创建者有权限更新,我们只能更新自己分支,然后创建合并请求&…...

cuda conda yolov11 环境搭建
优雅的 yolo v11 标注工具 AutoLabel Conda环境直接识别训练 nvidia-smi 检查CUDA版本 下载nvidia cudnn对应的版本 将cuDNN压缩包内对应的文件复制到本地bin、include、lib的文件夹中 C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v12.6 miniConda快速开始-安装 执行…...

解决SpringBoot连接Websocket报:请求路径 404 No static resource websocket.
问题发现 最近在工作中用到了WebSocket进行前后端的消息通信,后端代码编写完后,测试一下是否连接成功,发现报No static resource websocket.,看这个错貌似将接口变成了静态资源来访问了,第一时间觉得是端点没有注册成…...

element-plus的组件数据配置化封装 - table
目录 一、封装的table、table-column组件以及相关ts类型的定义 1、ATable组件的封装 - index.ts 2、ATableColumn组件的封装 - ATableColumn.ts 3、ATable、ATableColumn类型 - interface.ts 二、ATable、ATableColumn组件的使用 三、相关属性、方法的使用以及相关说明 1. C…...

【二维动态规划:交错字符串】
介绍 编程语言:Java 本篇介绍一道比较经典的二维动态规划题。 交错字符串 主要说明几点: 为什么双指针解不了?为什么是二维动态规划?根据题意分析处转移方程。严格位置依赖和空间压缩优化。 题目介绍 题意有点抽象,…...

goframe开发一个企业网站 MongoDB 完整工具包18
1. MongoDB 工具包完整实现 (mongodb.go) package mongodbimport ("context""fmt""time""github.com/gogf/gf/v2/frame/g""go.mongodb.org/mongo-driver/mongo""go.mongodb.org/mongo-driver/mongo/options" )va…...

在vue中,根据后端接口返回的文件流实现word文件弹窗预览
需求 弹窗预览word文件,因浏览器无法直接根据blob路径直接预览word文件,所以需要利用插件实现。 解决方案 利用docx-preview实现word文件弹窗预览,以node版本16.21.3和docx-preview版本0.1.8为例 具体实现步骤 1、安装docx-preview插件 …...

动态规划之背包问题
0/1背包问题 1.二维数组解法 题目描述:有一个容量为m的背包,还有n个物品,他们的重量分别为w1、w2、w3.....wn,他们的价值分别为v1、v2、v3......vn。每个物品只能使用一次,求可以放进背包物品的最大价值。 输入样例…...

【Python】 深入理解Python的单元测试:用unittest和pytest进行测试驱动开发
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 单元测试是现代软件开发中的重要组成部分,通过验证代码的功能性、准确性和稳定性,提升代码质量和开发效率。本文章深入介绍Python中两种主流单元测试框架:unittest和pytest,并结合测试驱动开发(TDD)…...

Java集合1.0
1.什么是集合? 集合就是一个存放数据的容器,准确的说是放数据对象引用的容器。 集合和数组的区别 数组是固定长度,集合是可变长度。数组可以存储基本数据类型,也可以存储引用数据类型,集合只能存储引用数据类型&…...

Leetcode 336 回文对
示例 1: 输入:words ["abcd","dcba","lls","s","sssll"] 输出:[[0,1],[1,0],[3,2],[2,4]] 解释:可拼接成的回文串为 ["dcbaabcd","abcddcba","sl…...

实现一个可配置的TCP设备模拟器,支持交互和解析配置
前言 诸位在做IOT开发的时候是否有遇到一个问题,那就是模拟一个设备来联调测试,虽然说现在的物联网通信主要是用mqtt通信,但还是有很多设备使用TCP这种协议交互,例如充电桩,还有一些工业设备,TCP这类报文交…...

算法的空间复杂度
空间复杂度 空间复杂度主要是衡量一个算法运行所需要的额外空间,在计算机发展早期,计算机的储存容量很小,所以空间复杂度是很重要的。但是经过计算机行业的迅速发展,计算机的容量已经不再是问题了,所以如今已经不再需…...
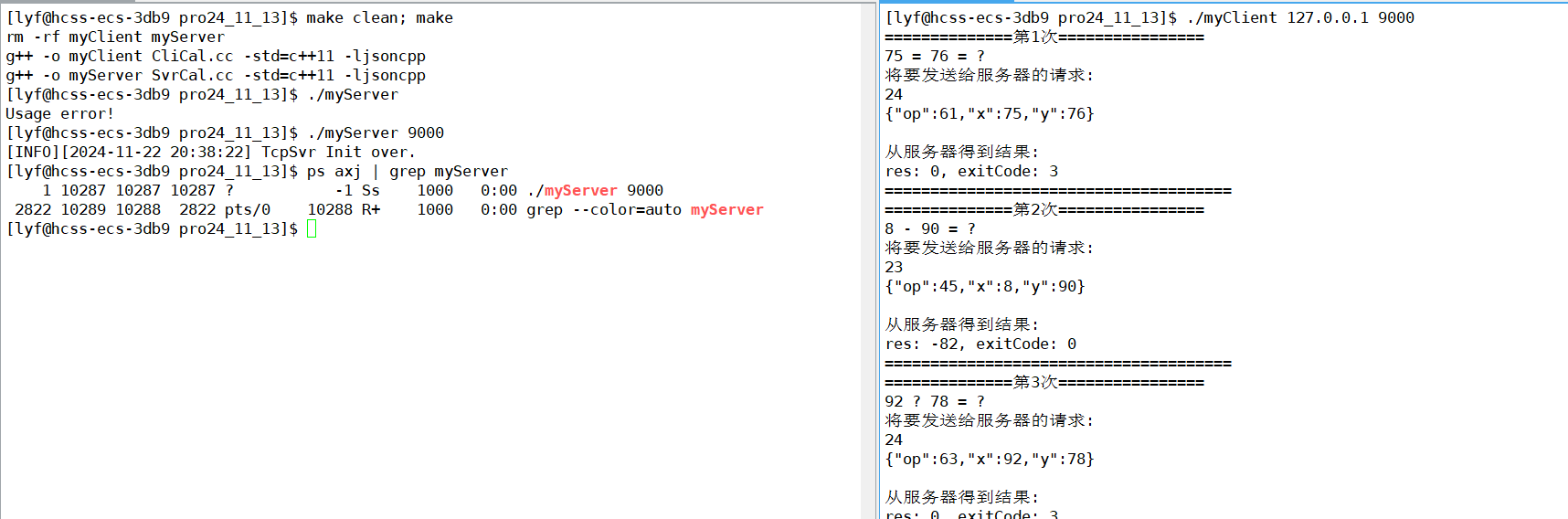
自定义协议
1. 问题引入 问题:TCP是面向字节流的(TCP不关心发送的数据是消息、文件还是其他任何类型的数据。它简单地将所有数据视为一个字节序列,即字节流。这意味着TCP不会对发送的数据进行任何特定的边界划分,它只是确保数据的顺序和完整…...

在 Taro 中实现系统主题适配:亮/暗模式
目录 背景实现方案方案一:CSS 变量 prefers-color-scheme 媒体查询什么是 prefers-color-scheme?代码示例 方案二:通过 JavaScript 监听系统主题切换 背景 用Taro开发的微信小程序,需求是页面的UI主题想要跟随手机系统的主题适配…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
)
iOS 项目怎么构建稳定性保障机制?一次系统性防错经验分享(含 KeyMob 工具应用)
崩溃、内存飙升、后台任务未释放、页面卡顿、日志丢失——稳定性问题,不一定会立刻崩,但一旦积累,就是“上线后救不回来的代价”。 稳定性保障不是某个工具的功能,而是一套贯穿开发、测试、上线全流程的“观测分析防范”机制。 …...

Vue3项目实现WPS文件预览和内容回填功能
技术方案背景:根据项目需要,要实现在线查看、在线编辑文档,并且进行内容的快速回填,根据这一项目背景,最终采用WPS的API来实现,接下来我们一起来实现项目功能。 1.首先需要先准备好测试使用的文档…...

数据结构——D/串
一、串的定义和基本操作  1. 串的定义   1)串的概念   组成结构: 串是由零个或多个字符组成的有限序列,记为 S′a1a2⋯an′Sa_1a_2\cdots a_nS′a1a2⋯an′&#x…...

