【java数据结构】二叉树OJ题
【java数据结构】二叉树OJ题
- 一、检查两颗树是否相同
- 二、另一颗树的子树
- 三、翻转二叉树
- 四、对称二叉树
- 五、判断一颗二叉树是否是平衡二叉树
- 六、给定一个二叉树, 找到该树中两个指定节点的最近公共祖先
- 七、根据一棵树的前序遍历与中序遍历构造二叉树
- 练习:
- 八、二叉树前序非递归遍历实现
- 练习:
- 练习:
博客最后附有整篇博客的全部代码!!!
一、检查两颗树是否相同
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。

检查两颗树是否相同
解题思路:
1.先判断两棵树是否都为空,都为空则两棵树是相等的;反之一棵树为空,另一棵树不为空,则两棵树不是相同二叉树。
2.分别进行遍历两棵树的左右节点,判断其节点的值是否相等。
public boolean isSameTree(TreeNode p, TreeNode q) {if(p==null&&q==null)return true;if(p==null||q==null)return false;if(p.val!=q.val){return false;}return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}
二、另一颗树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。


另一颗树的子树
解题思路1:
1.先判断SubRoot是否为空,为空则一定是子树;下来判断Root是否为空,为空则返回false。
2.自己定义了一个方法isSame(TreeNode p,TreeNode q)来判断遍历的树的左右节点的值是否相同。
3. return isSubtree(root.left,subRoot)||
4. isSubtree(root.right,subRoot)||isSame(root,subRoot);这段代码的意思:先用isSubtree(TreeNode root, TreeNode subRoot)这个方法遍历Root树的左右节点,然后每当遍历到一个节点的时候,都将该节点作为Root节点的树和SubRoot树传入到isSame(TreeNode p,TreeNode q)这个方法中进行判断这两棵树是否相同,但凡相同则返回true;反之,如果遍历完每个节点都和SubRoot树没有完全相同的树,则SubRoot就不是Root树的子树。
public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(subRoot==null)return true;if(root==null)return false;return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot)||isSame(root,subRoot);}public boolean isSame(TreeNode p,TreeNode q){if(p==null&&q==null)return true;if(p==null||q==null||p.val!=q.val)return false;return isSame(p.left,q.left)&&isSame(p.right,q.right);}
三、翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。

翻转二叉树
解题思路:
1.先判断Root树是否为空,为空则返回null。
2.递归树的每一个节点的左右节点,并用定义的TreeNode类型的left和right来进行接收每一个节点的左右节点。
3.最后将left和right互换。
public TreeNode invertTree(TreeNode root) {if(root==null)return null;TreeNode left=invertTree(root.left);TreeNode right=invertTree(root.right);root.left=right;root.right=left;return root;}
四、对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。

对称二叉树
解题思路:
和判断两棵树是否相同的思路相等,不同点是判断的是p的左节点和q的右节点、p的右节点和q的左节点是否相同。
public boolean isSymmetric(TreeNode root) {if(root==null)return true;TreeNode p=root.left;TreeNode q=root.right;return isSame(p,q);}public boolean isSame(TreeNode p,TreeNode q){if(p==null&&q==null)return true;if(p==null||q==null||p.val!=q.val)return false;return isSame(p.left,q.right)&&isSame(p.right,q.left);}
五、判断一颗二叉树是否是平衡二叉树
给定一个二叉树,判断它是否是 平衡二叉树。

判断一颗二叉树是否是平衡二叉树
解题思路1:
时间复杂度为:O(N^2)
1.先判断树是否为空。
2.遍历每一个节点,求每一个节点的左右高度,判断该节点的左右高度差是否大于1。
public boolean isBalanced(TreeNode root) {if(root==null)return true;int leftHight=getHeight(root.left);int rightHight=getHeight(root.right);return Math.abs(leftHight-rightHight)<=1 && isBalanced(root.left) && isBalanced(root.right);}int getHeight(TreeNode root) {if (root == null) return 0;int leftH = getHeight(root.left);int rightH = getHeight(root.right);return leftH > rightH ? leftH + 1 : rightH + 1;}
解题思路2:
时间复杂度:O(N)。
自下而上计算每个节点的高度,判断每个节点是否是平衡二叉树,如果是返回该节点的高度,反之返回-1。
public boolean isBalanced2(TreeNode root) {return getHeight2(root)>=0;}int getHeight2(TreeNode root) {if (root == null) return 0;int leftH = getHeight2(root.left);if(leftH<0){return -1;}int rightH = getHeight2(root.right);if(rightH>=0&&Math.abs(leftH - rightH) <= 1){return Math.max(leftH, rightH) + 1;}return -1;}
六、给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先
解题思路1:
1.先判断树是否为空,为空则返回null。
2.开始遍历树的每一个节点,找到p或q的节点,然后返回。
3.如果都找到了则返回Root节点,这里的Root节点肯定不是p或q的本身;如果没找到q节点,则公共祖先就是q节点;反之。
(此思路,当找到一个节点时,就不会继续遍历该节点的子节点)。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null)return null;if(root==p||root==q)return root;TreeNode lefttree=lowestCommonAncestor(root.left,p,q);TreeNode righttree=lowestCommonAncestor(root.right,p,q);if(lefttree!=null&&righttree!=null){return root;}else if(lefttree!=null){return lefttree;}else{return righttree;}}
解题思路2:
1.定义两个栈s1,s2。用来保存root节点到目标节点p、q的节点数。
2.判断两个栈的长度,pop()出栈中元素个数多的栈,让两个栈中元素个数相同。
3.peek()两个栈栈顶元素,判断是否相同,相同则就是公共祖先;不同则pop()出两栈顶元素。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {Stack<TreeNode> s1=new Stack<>();Stack<TreeNode> s2=new Stack<>();getPath(root,p,s1);getPath(root,q,s2);if(s1.size()>s2.size()){int len=s1.size()-s2.size();while(len!=0){s1.pop();len--;}}else{int len=s2.size()-s1.size();while(len!=0){s2.pop();len--;}}while(!s1.isEmpty()&&!s2.isEmpty()){if(s1.peek()==s2.peek()){return s1.peek();}else{s1.pop();s2.pop();}}return null;}public boolean getPath(TreeNode root,TreeNode target,Stack<TreeNode> stack){if(root==null) return false;stack.push(root);if(root==target) return true;if(getPath(root.left,target,stack)){return true;}if(getPath(root.right,target,stack)){return true;}stack.pop();return false;}
七、根据一棵树的前序遍历与中序遍历构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。

根据一棵树的前序遍历与中序遍历构造二叉树
解题思路:
1.定义一个:buildTreeChild(int[] preorder, int[] inorder,int inbegin,int inend)方法,用来构建二叉树,int[] preorder:前序遍历。 int[] inorder:中序遍历。int inbegin:标记中序遍历数组的起始位置。int inend:标记中序遍历数组的末尾。
2.定义一个私有方法:findVal(int[] inorder,int inbegin,int inend,int val),用来在中序遍历中找到根节点的位置。此时返回的int值左边的值就是左子树,右边的值就是右子树。
public int preIndex=0;public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTreeChild(preorder,inorder,0,inorder.length-1);}public TreeNode buildTreeChild(int[] preorder, int[] inorder,int inbegin,int inend) {//这种情况下 表明 当前root 没有子树了 if(inbegin > inend) {return null;}TreeNode root = new TreeNode(preorder[preIndex]);int rootIndex = findVal(inorder,inbegin,inend,preorder[preIndex]);preIndex++;root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);return root;}private int findVal(int[] inorder,int inbegin,int inend,int val) {for(int i = inbegin ;i <= inend;i++) {if(inorder[i] == val) {return i;}}return -1;}
练习:
根据一棵树的中序遍历与后序遍历构造二叉树
八、二叉树前序非递归遍历实现
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
 二叉树前序非递归遍历实现
二叉树前序非递归遍历实现
解题思路:
1.先判断root树是否为空。
2.定义一个栈和node=root;node开始往左遍历,遍历一个将node.val放入链表中,然后将node放入栈中;当node==null时,node=stack.pop();遍历node右边的。
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list=new ArrayList<>();if(root==null)return list;Stack<TreeNode> stack=new Stack<>();TreeNode node=root;while(node!=null||!stack.isEmpty()) {while (node != null) {list.add(node.val);stack.push(node);node = node.left;}node = stack.pop();node = node.right;}return list;}
练习:
二叉树的中序遍历非递归
练习:
二叉树的后序遍历非递归
此篇博客的全部代码!!!
相关文章:

【java数据结构】二叉树OJ题
【java数据结构】二叉树OJ题 一、检查两颗树是否相同二、另一颗树的子树三、翻转二叉树四、对称二叉树五、判断一颗二叉树是否是平衡二叉树六、给定一个二叉树, 找到该树中两个指定节点的最近公共祖先七、根据一棵树的前序遍历与中序遍历构造二叉树练习:八、二叉树前…...

IIC和SPI的时序图
SCL的变化快慢决定了通信速率,当SCL为低电平的时候,无论SDA是1还是0都不识别: ACK应答:当从设备为低电平的时候识别为从设备有应答: 谁接收,谁应答: 起始位和停止位: IIC的时序图&am…...

MySQL数据库表的操作
1、总述 今天我跟大家分享MySQL数据库中表的创建,查看,修改,删除。 2、创建表 create table table_name ( field1 datatype, field2 datatype, field3 datatype ) character set 字符集 collate 校验规则 engine 存储引擎; 说明࿱…...

.net core 创建linux服务,并实现服务的自我更新
目录 创建服务创建另一个服务,用于执行更新操作给你的用户配置一些systemctl命令权限 创建服务 /etc/systemd/system下新建服务配置文件:yourapp.service,内容如下: [Unit] Descriptionyourapp Afternetwork.target[Service] Ty…...

springboot338it职业生涯规划系统--论文pf(论文+源码)_kaic
毕 业 设 计(论 文) 题目:it职业生涯规划系统的设计与实现 摘 要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以…...

oracle将select作为字段查询
在Oracle中,如果你想将一个SELECT语句作为字段的值,你可以使用子查询或者使用WITH子句(也称为公用表表达式CTE)。以下是两种方法的示例: 方法1:使用子查询 语法如下: SELECTcolumn1,(SELECT …...

Java数据结构和算法相关面试题
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...
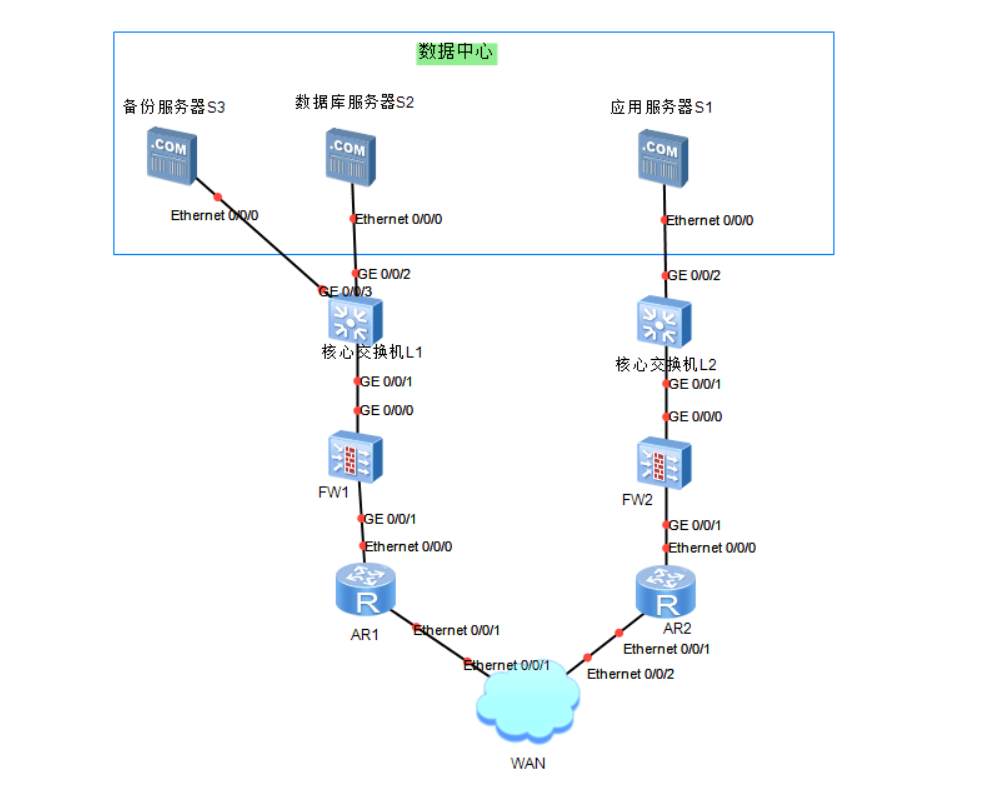
网络安全风险评估
项目背景 随着信息化技术的快速发展,特别是面向社会、政府机构、企业等业务系统的投入使用,各组织机构对网络和信息系统安全防护都提出了新的要求。为满足安全需求,需对组织机构的网络和信息系统的安全进行一次系统全面的评估,以…...

ADAM优化算法与学习率调度器:深度学习中的关键工具
深度学习模型的训练效果离不开优化算法和学习率的选择。ADAM(Adaptive Moment Estimation)作为深度学习领域中广泛应用的优化算法之一,以其高效性和鲁棒性成为许多任务的默认选择。而学习率调度器则是优化算法的“助推器”,帮助训…...

岛屿数量C++11新特性
每日一题 200. 岛屿数量 class Solution {//使用深度的优先搜索来搜索岛屿图//遍历整个图片 当char数组的值为1时开始从这个点开始往外扩散搜索//注意处理边界 图不是正方形 public:int ans;int d[4][2] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};int N;int M;void dfs(vector<…...

Git 快速入门:全面了解与安装步骤
Git 快速入门:全面了解与安装步骤 一、关于Git 1.1 简介 Git 是一个开源的分布式版本控制系统,由 Linus Torvalds 于 2005 年创建,最初是为了更好地管理 Linux 内核开发而设计。 Git用于跟踪计算机文件的变化,特别是源代码文件…...

基于域自适应的双光融合
目录 引言DAF-Net编码器-解码器分支编码器部分融合层解码器部分 域自适应层概述多核最大均值差异(MK-MMD)第一阶段:编码器-解码器分支训练训练过程损失函数 第二阶段:融合层训练训练过程损失函数 实验与结果总结 文章声明…...
)
迭代器模式 (Iterator Pattern)
文章目录 迭代器模式 (Iterator Pattern)原理优点缺点示例代码场景描述1. 定义迭代器接口2. 定义集合接口3. 实现具体集合类4. 客户端代码输出结果 UML 类图使用场景优化与扩展小结 迭代器模式 (Iterator Pattern) 迭代器模式是一种 行为型设计模式,用于顺序访问集…...

039集——渐变色之:CAD中画彩虹()(CAD—C#二次开发入门)
(来左边儿 跟我一起画个龙,在你右边儿 画一道彩虹 ~~~~~~~~~~~ ) 效果如下: namespace AcTools {public class Class1{public Wform.Timer timer;//定时器需建在类下面public static DateTime startTime;[CommandM…...

如何将 GitHub 私有仓库(private)转换为公共仓库(public)
文章目录 如何将 GitHub 私有仓库转换为公共仓库步骤 1: 登录 GitHub步骤 2: 导航到目标仓库步骤 3: 访问仓库设置步骤 4: 更改仓库可见性步骤 5: 确认更改步骤 6: 验证更改注意事项 如何将 GitHub 私有仓库转换为公共仓库 在软件开发领域,GitHub 是一个广受欢迎的…...

C++11 右值引用
目录 左值 右值 左值引用与右值引用比较 左值引用总结: 右值引用总结: 左值引用的使用场景: 引用传参和做返回值都可以提高效率(减少拷贝) 左值引用的短板: 右值引用和移动语义解决上述问题: 下面就是有移动…...

WPS表格学习计划与策略
一、学习目标 掌握WPS表格的基本操作:包括新建、打开、保存工作簿,单元格的编辑与格式化,数据的输入与验证等。熟练运用WPS表格的数据处理功能:包括数据排序、筛选、分类汇总,以及使用公式和函数进行计算和分析。学会制作图表与数据可视化:掌握不同类型图表(如柱状图、折…...

Android 引入 proto 项目及使用方法
Proto(Protocol Buffers)是Google开发的一种语言无关、平台无关的序列化结构数据的方法,它类似于JSON和XML,但相对于XML而言更小,相对于JSON而言解析更快,支持多语言。以下是将Proto引入Android项目的方法及…...

VSOMEIP主要流程的时序
请求服务: client应用: application_impl::request_service routing_manager_client::request_service (老版本是routing_manager_proxy) routing_manager_client::send_request_services protocol::request_service_command its_command; // 创建…...

右值引用和移动语义:
C 右值引用和移动语义详解 在 C 的发展历程中,右值引用和移动语义的引入带来了显著的性能提升和编程灵活性。本文将深入探讨右值引用和移动语义的概念、用法以及重要性。 一、引言 C 作为一门高效的编程语言,一直在不断演进以满足现代软件编程的需求。…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
