数据结构 (17)广义表
前言
数据结构中的广义表(Generalized List,又称列表Lists)是一种重要的数据结构,它是对线性表的一种推广,放松了对表元素的原子限制,容许它们具有其自身的结构。
一、定义与表示
- 定义:广义表是n(n≥0)个元素a1, a2, …, ai, …, an的有限序列,其中每个元素ai可以是原子(即不可再分的元素),也可以是另一个广义表。
- 表示:广义表通常记作Ls = (a1, a2, …, ai, …, an),其中Ls是广义表的名字,n为它的长度。若ai是广义表,则称它为Ls的子表。
二、特征
- 线性结构:广义表是一种线性结构,其长度为最外层包含的元素个数。
- 多层次结构:广义表中的元素可以是子表,而子表的元素还可以是子表,因此广义表是一种多层次的结构。
- 共享性:一个广义表可以为其他广义表所共享。
- 递归性:广义表的定义是递归的,即广义表可以包含其他广义表作为元素。
三、存储结构
广义表的存储方式有多种,主要包括线性链表、顺序存储和树状结构:
线性链表:
- 是广义表最常见的存储方式之一。
- 由一系列节点组成,每个节点包含一个元素和一个指向下一个节点的指针。
- 通过不断跟踪下一个节点的指针,可以遍历整个链表,实现对广义表的操作。
- 适用于不同长度的广义表,可以方便地进行插入、删除和修改操作,但需要较多的内存空间来存储指针。
顺序存储:
- 将广义表的元素按顺序存储在一个连续的内存空间中。
- 适用于广义表长度已知且固定的情况。
- 占用的内存空间较少,访问元素的效率也较高,但插入和删除操作较为复杂,需要移动其他元素的位置。
树状结构:
- 将广义表表示为一个树,每个节点包含一个元素和若干子节点。
- 适用于具有层次结构的广义表。
- 可以方便地进行递归操作,但需要较多的内存空间来存储节点。
四、基本运算
广义表的基本运算包括但不限于以下几种:
- 取表头head(Ls):任何一个非空广义表的表头是表中第一个元素,它可以是原子,也可以是子表。
- 取表尾tail(Ls):广义表的表尾是除去表头后其余元素组成的表,表尾必定是子表。
- 求深度:广义表的深度定义为它等于所有子表中表的最大深度加1。若一个表为空或仅由单个元素所组成,则深度为1。
- 反转:将广义表的元素顺序反转,得到一个新的广义表。
- 遍历:按照一定规则访问广义表中的每个元素,并对其进行相应的操作。
- 查找:在广义表中查找满足特定条件的元素或子表。
- 插入与删除:在广义表的指定位置插入或删除元素,这通常涉及到链表的节点操作或数组的元素移动。
五、应用场景
广义表可以广泛应用于各种实际应用场景,包括但不限于:
- 存储传感器数据:在物联网系统中,传感器收集的数据可以被表示为广义表,以便进行比较和关联分析。
- 文本处理:在自然语言处理中,广义表可以用来表示文本数据,如单词、短语和句子等,以便进行分词、句法分析和语义分析等操作。
- 图像处理:在图像处理中,广义表可以用来表示图像的各个部分,如像素、颜色和形状等,以便进行滤波、分割和特征提取等操作。
- 社交网络分析:在社交网络分析中,广义表可以用来表示社交网络中的节点和关系,以便进行关键节点检测、社区检测和网络流量分析等操作。
- 用户行为分析:在电子商务或社交媒体平台上,用户行为数据可以被表示为广义表,以便进行分析和预测,以优化平台功能和提供更好的用户体验。
- 数据库管理系统:在数据库管理系统中,广义表可以用来表示各种数据结构,以便进行查询优化和数据挖掘等操作。
总结
综上所述,广义表是一种功能强大且灵活的数据结构,适用于各种复杂的数据处理和分析任务。
![]() 结语
结语
后悔过去
不如奋斗将来
!!!

相关文章:

数据结构 (17)广义表
前言 数据结构中的广义表(Generalized List,又称列表Lists)是一种重要的数据结构,它是对线性表的一种推广,放松了对表元素的原子限制,容许它们具有其自身的结构。 一、定义与表示 定义:广义表是…...

论文笔记 SliceGPT: Compress Large Language Models By Deleting Rows And Columns
欲买桂花同载酒,终不似,少年游。 数学知识 秩: 矩阵中最大线性无关的行/列向量数。行秩与列秩相等。 线性无关:对于N个向量而言,如果任取一个向量 v \textbf{v} v,不能被剩下的N-1个向量通过线性组合的方式…...

前端工具的选择和安装
选择和安装前端工具是前端开发过程中的重要步骤。现代前端开发需要一些工具来提高效率和协作能力。以下是一些常用的前端工具及其选择和安装指南。 1. 代码编辑器 选择一个好的代码编辑器可以显著提高开发效率。以下是几款流行的代码编辑器: Visual Studio Code (…...

Fantasy中定时器得驱动原理
一、服务器框架启动 public static async FTask Start(){// 启动ProcessStartProcess().Coroutine();await FTask.CompletedTask;while (true){ThreadScheduler.Update();Thread.Sleep(1);}} 二、主线程 Fantasy.ThreadScheduler.Update internal static void Update(){MainS…...

【反转链表】力扣 445. 两数相加 II
一、题目 二、思路 加法运算是从低位开始,向高位进位,因此需要将两个链表进行反转,再进行对齐后的相加操作。力扣 2. 两数相加 三、题解 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode …...

SpringBoot 项目中使用 spring-boot-starter-amqp 依赖实现 RabbitMQ
文章目录 前言1、application.yml2、RabbitMqConfig3、MqMessage4、MqMessageItem5、DirectMode6、StateConsumer:消费者7、InfoConsumer:消费者 前言 本文是工作之余的随手记,记录在工作期间使用 RabbitMQ 的笔记。 1、application.yml 使…...

Uniapp 安装安卓、IOS模拟器并调试
一、安装Android模拟器并调试 1. 下载并安装 Android Studio 首先下载 Mac 环境下的 Android Studio 的安装包,为dmg 格式。 下载完将Android Studio 向右拖拽到Applications中,接下来等待安装完成就OK啦! 打开过程界面如下图所示…...

JavaScript 中的原型和原型链
JavaScript 中的原型和原型链也是一个相对较难理解透彻的知识点,下面结合详细例子来进行说明: 一、原型的概念 在 JavaScript 中,每个函数都有一个 prototype 属性,这个属性指向一个对象,这个对象就是所谓的 “原型对…...

数组变换(两倍)
数组变换 以最大元素为基准元素,判读其他元素能否通过 x 2 成为最大值! 那么怎么判断呢: max % arr[i] 0arr[i] * 2 ^n max int x 2 ^ n max / arr[i] 3.只需判断 这个 x 是不是 2 的 n 次放就可以了! 判断 是否为 2 的 n 次 …...

GBN协议、SR协议
1、回退N步(Go-Back-N,GBN)协议: 总结: GBN协议的特点: (1)累计确认机制:当发送方收到ACKn时,表明接收方已正确接收序号为n以及序号小于n的所有分组,发送窗…...

三维扫描检测仪3d扫描测量尺寸-自动蓝光测量
在现代工业及生产过程中,精确、高效的尺寸检测是保证产品质量、提升生产效率的关键因素。 红、蓝光测量,以其高精度、高效率和非接触式的特点,在工业及生产中发挥着越来越重要的作用。蓝光测量技术利用蓝色激光光源,通过扫描被测…...

大模型翻译能力评测
1. 背景介绍 随着自然语言处理技术的飞速发展,机器翻译已经成为一个重要的研究领域。近年来,基于大模型的语言模型在机器翻译任务上取得了显著的进展。这些大模型通常具有数亿甚至数千亿的参数,能够更好地理解和生成自然语言。 但是…...

MySQL隐式转换造成索引失效
一、什么是 MySQL 的隐式转换? MySQL 在执行查询语句时,有时候会自动帮我们进行数据类型的转换,这个过程就是隐式转换。比如说,我们在一个 INT 类型的字段上进行查询,但是传入的查询条件却是字符串类型的值,…...

SuperMap Objects组件式GIS开发技术浅析
引言 随着GIS应用领域的扩展,GIS开发工作日显重要。一般地,从平台和模式上划分,GIS二次开发主要有三种实现方式:独立开发、单纯二次开发和集成二次开发。上述的GIS应用开发方式各有利弊,其中集成二次开发既可以充分利…...

多组数输入a+b:JAVA
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 输入描述: 输入包含多组数据,每组数据输入一行,包含两个整数 输出描述: 对于每组数据输出一行包含一个整数表示两个整数的和 代码: import java.util.Scanner; pu…...

R语言结构方程模型(SEM)在生态学领域中的应用
目录 专题一、R/Rstudio简介及入门 专题二、结构方程模型(SEM)介绍 专题三:R语言SEM分析入门:lavaan VS piecewiseSEM 专题四:SEM全局估计(lavaan)在生态学领域高阶应用 专题五࿱…...

架构-微服务-服务调用Dubbo
文章目录 前言一、Dubbo介绍1. 什么是Dubbo 二、实现1. 提供统一业务api2. 提供服务提供者3. 提供服务消费者 前言 服务调用方案--Dubbo 基于 Java 的高性能 RPC分布式服务框架,致力于提供高性能和透明化的 RPC远程服务调用方案,以及SOA服务治理方案。…...

【SpringBoot问题】IDEA中用Service窗口展示所有服务及端口的办法
1、调出Service窗口 打开View→Tool Windows→Service,即可显示。 2、正常情况应该已经出现SpringBoot,如下图请继续第三步 3、配置Service窗口的项目启动类型。微服务一般是Springboot类型。所以这里需要选择一下。 点击最后一个号,点击Ru…...
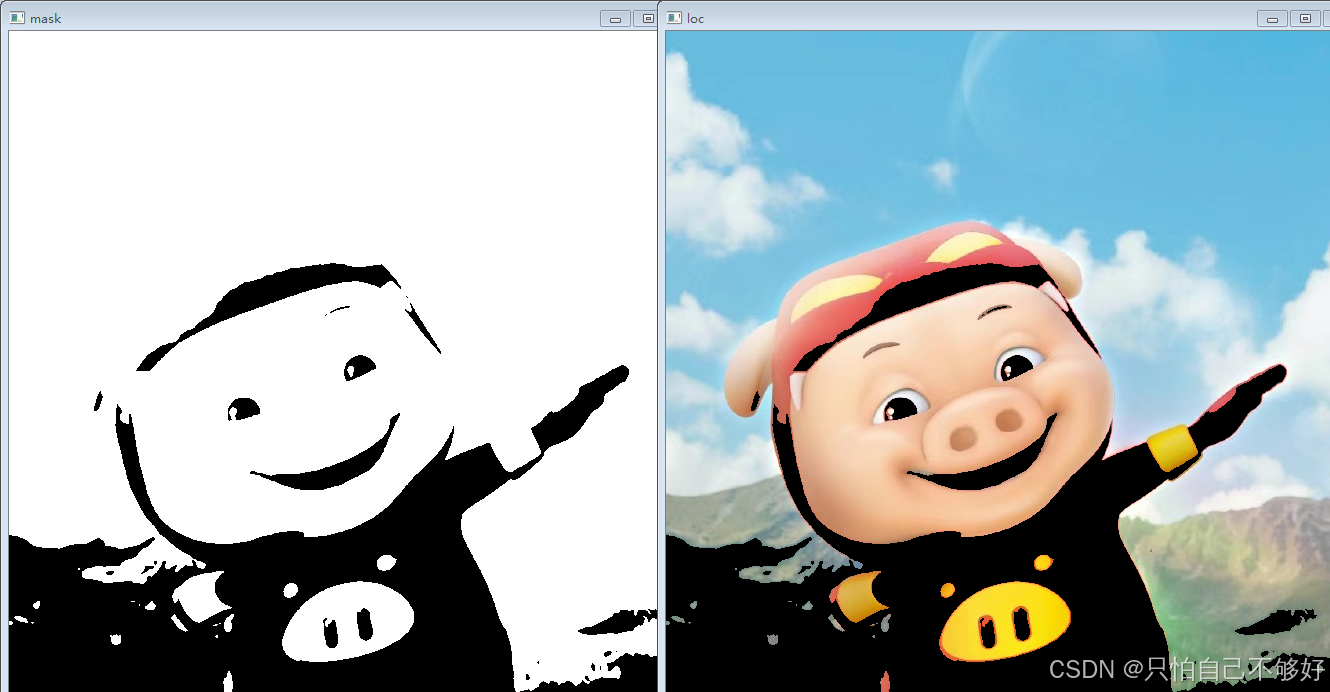
OpenCV 图像轮廓查找与绘制全攻略:从函数使用到实战应用详解
摘要:本文详细介绍了 OpenCV 中用于查找图像轮廓的 cv2.findContours() 函数以及绘制轮廓的 cv2.drawContours() 函数的使用方法。涵盖 cv2.findContours() 各参数(如 mode 不同取值对应不同轮廓检索模式)及返回值的详细解析,搭配…...

电机驱动MCU介绍
电机驱动MCU是一种专为电机控制设计的微控制器单元,它集成了先进的控制算法和高性能的功率输出能力。 电机驱动MCU采用高性能的处理器核心,具有快速的运算速度和丰富的外设接口。它内置了专业的电机控制算法,包括PID控制、FOC(Fi…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
