迪米特原则的理解和实践
迪米特原则(Law of Demeter,简称LoD),也被称为最少知识原则(Least Knowledge Principle,LKP),是面向对象设计中的一个重要原则。其核心思想是:一个对象应该对其他对象有最少的了解,即一个对象应该尽可能少地了解其直接对象之外的任何对象。本文将详细探讨迪米特原则的理论理解及其在Java实践中的应用。
一、迪米特原则的理论理解
迪米特原则的核心在于降低类之间的耦合度,提高模块的相对独立性。通过封装和信息隐藏,对象之间的通信应该通过抽象层进行,以减少对象之间的直接依赖。这种设计方式能够提高系统的可维护性和可扩展性,降低代码的依赖性,减少系统中的风险因素。
-
降低耦合度:
耦合度是指不同模块之间相互依赖的程度。过高的耦合度会导致代码难以维护和扩展。迪米特原则通过限制对象之间的直接通信,促使开发者使用接口或中间层来进行通信,从而有效地降低系统各部分之间的耦合度。 -
提高内聚力:
内聚力是指模块内部各元素间的紧密程度。高内聚力的模块功能更加专一,易于理解和修改。迪米特原则通过限制对象间的直接交流,促使开发者将功能相似的代码组织在一起,提高了模块的内聚力。 -
便于测试和重用:
通过遵循迪米特原则,每个类的功能更加单一和明确,这有助于对单个功能进行独立的测试,从而提高代码的可测试性。同时,减少类之间的直接依赖关系,使得类更加容易重用。 -
增强系统的可扩展性:
通过降低类之间的耦合,迪米特原则使得系统的某个部分在不改变其他部分的情况下可以进行修改或扩展,从而增强了系统的可扩展性。
二、迪米特原则的实践
在Java开发中,迪米特原则可以通过多种方式来实现,包括中介者模式、控制反转(IoC)和依赖注入(DI)、事件驱动编程以及模块化设计等。下面通过具体的代码示例来展示迪米特原则的实践。
示例一:中介者模式
当一个类需要与多个类进行交互时,可以使用中介者模式来降低类之间的直接依赖。中介者负责协调各个类之间的交互,从而减少类之间的直接通信。
// 中介者接口
interface Mediator {void send(String message, String colleagueName);
}// 具体中介者类
class ConcreteMediator implements Mediator {private ColleagueA colleagueA;private ColleagueB colleagueB;public void setColleagueA(ColleagueA colleagueA) {this.colleagueA = colleagueA;}public void setColleagueB(ColleagueB colleagueB) {this.colleagueB = colleagueB;}@Overridepublic void send(String message, String colleagueName) {if ("A".equals(colleagueName)) {colleagueA.receive(message);} else if ("B".equals(colleagueName)) {colleagueB.receive(message);}}
}// 同事类A
class ColleagueA {private Mediator mediator;public void setMediator(Mediator mediator) {this.mediator = mediator;}public void send(String message) {mediator.send(message, "B");}public void receive(String message) {System.out.println("ColleagueA received: " + message);}
}// 同事类B
class ColleagueB {private Mediator mediator;public void setMediator(Mediator mediator) {this.mediator = mediator;}public void send(String message) {mediator.send(message, "A");}public void receive(String message) {System.out.println("ColleagueB received: " + message);}
}// 测试类
public class MediatorPatternDemo {public static void main(String[] args) {Mediator mediator = new ConcreteMediator();ColleagueA colleagueA = new ColleagueA();ColleagueB colleagueB = new ColleagueB();mediator.setColleagueA(colleagueA);mediator.setColleagueB(colleagueB);colleagueA.setMediator(mediator);colleagueB.setMediator(mediator);colleagueA.send("Hello B");colleagueB.send("Hello A");}
} 在这个示例中,ColleagueA 和 ColleagueB 通过 Mediator 进行通信,而不是直接调用对方的方法。这降低了类之间的耦合度,提高了系统的可维护性和可扩展性。
示例二:控制反转(IoC)和依赖注入(DI)
控制反转和依赖注入允许我们将依赖关系外部化,并由容器或框架来管理。这样,类之间的依赖关系就变得更加灵活,降低了直接耦合。
// 接口
interface Service {void execute();
}// 具体服务类
class ConcreteService implements Service {@Overridepublic void execute() {System.out.println("Service executed");}
}// 客户端类
class Client {private Service service;// 构造器注入public Client(Service service) {this.service = service;}public void doSomething() {service.execute();}
}// 测试类
public class IoCDemo {public static void main(String[] args) {Service service = new ConcreteService();Client client = new Client(service);client.doSomething();}
} 在这个示例中,Client 类通过构造器注入的方式依赖 Service 接口,而不是直接依赖 ConcreteService 类。这使得 Client 类更加灵活,可以轻松地替换 Service 的实现。
示例三:迪米特原则的反面示例与推荐用法
下面通过一个业务场景来展示迪米特原则的反面示例和推荐用法。
反面示例:
// 经理类
public class Manager {public void checkGoodsCount(Staff staff) {List<Good> goodList = new ArrayList<>();for (int i = 0; i < 20; i++) {goodList.add(new Good());}staff.checkCount(goodList);}
}// 员工类
public class Staff {public void checkCount(List<Good> goodList) {System.out.println("商品数量为: " + goodList.size());}
}// 商品类
public class Good {
}// 测试类
public class Main {public static void main(String[] args) {Manager manager = new Manager();Staff staff = new Staff();manager.checkGoodsCount(staff);}
} 在这个反面示例中,Manager 类直接创建了 Good 对象的列表,并将其传递给 Staff 类。这违反了迪米特原则,因为 Manager 类不应该了解 Good 类的具体实现。
推荐用法:
// 经理类
public class Manager {public void checkGoodsCount(Staff staff) {staff.checkCount();}
}// 员工类
public class Staff {public void checkCount() {List<Good> goodList = new ArrayList<>();for (int i = 0; i < 20; i++) {goodList.add(new Good());}System.out.println("商品数量为: " + goodList.size());}
}// 商品类
public class Good {
}// 测试类
public class Main {public static void main(String[] args) {Manager manager = new Manager();Staff staff = new Staff();manager.checkGoodsCount(staff);}
} 在推荐用法中,Manager 类不再直接创建 Good 对象的列表,而是将创建列表的责任交给了 Staff 类。这样,Manager 类只需要知道 Staff 类的接口,而不需要了解 Good 类的具体实现,从而遵循了迪米特原则。
三、总结
迪米特原则是面向对象设计中的一个重要原则,它强调一个对象应该对其他对象有最少的了解。通过降低类之间的耦合度,提高模块的相对独立性,迪米特原则有助于我们设计出更加灵活、可维护性更高的软件系统。在Java开发中,我们可以利用中介者模式、控制反转(IoC)和依赖注入(DI)、事件驱动编程以及模块化设计等技术来实现迪米特原则。然而,过分追求迪米特原则可能导致设计过于复杂,增加不必要的抽象层和中介者。因此,在使用迪米特原则时应适度应用,结合其他设计原则,关注实际场景,避免盲目追求理论上的完美设计。
相关文章:

迪米特原则的理解和实践
迪米特原则(Law of Demeter,简称LoD),也被称为最少知识原则(Least Knowledge Principle,LKP),是面向对象设计中的一个重要原则。其核心思想是:一个对象应该对其他对象有最…...
)
jQuery零基础入门速通(中)
大家好,我是小黄。 在上一篇文章中,我们初步了解了jQuery的基本概念、环境搭建、选择器、基本的DOM操作以及事件处理。接下来,我们将继续深入探讨jQuery的DOM操作和事件处理,以及一些实用的技巧和高级用法。 五、高级DOM操作 5…...

【设计模式系列】中介者模式(十八)
一、什么是中介者模式 中介者模式(Mediator Pattern)是一种行为型设计模式,其核心思想是通过一个中介者对象来封装一系列对象之间的交互,使这些对象不需要相互显式引用。中介者模式提供了一个中介层,用以协调各个对象…...

PDF版地形图矢量出现的问题
项目描述:已建风电场道路测绘项目,收集到的数据为PDF版本的地形图,图上标注了项目竣工时期的现状,之后项目对施工区域进行了复垦恢复地貌,现阶段需要准确的知道实际复垦修复之后的道路及其它临时用地的面积 解决方法&…...

小迪安全第四十二天笔记 简单的mysql注入 mysql的基础知识 用户管理数据库模式 mysql 写入与读取 跨库查询
前言 之前的安全开发我们学习了 php联动数据库的模式 ,这个模式是现在常用的模式 这一节来学习 如何 进行数据库的注入和数据库相关知识 1、了解数据库的结构 我们使用 navicate连接数据库之后看一下 一共四层结构 库 》表》字段》数据 这个层级关系…...

11.25.2024刷华为OD
文章目录 HJ76 尼科彻斯定理(观察题,不难)HJ77 火车进站(DFS)HJ91 走格子方法,(动态规划,递归,有代表性)HJ93 数组分组(递归)语法知识…...
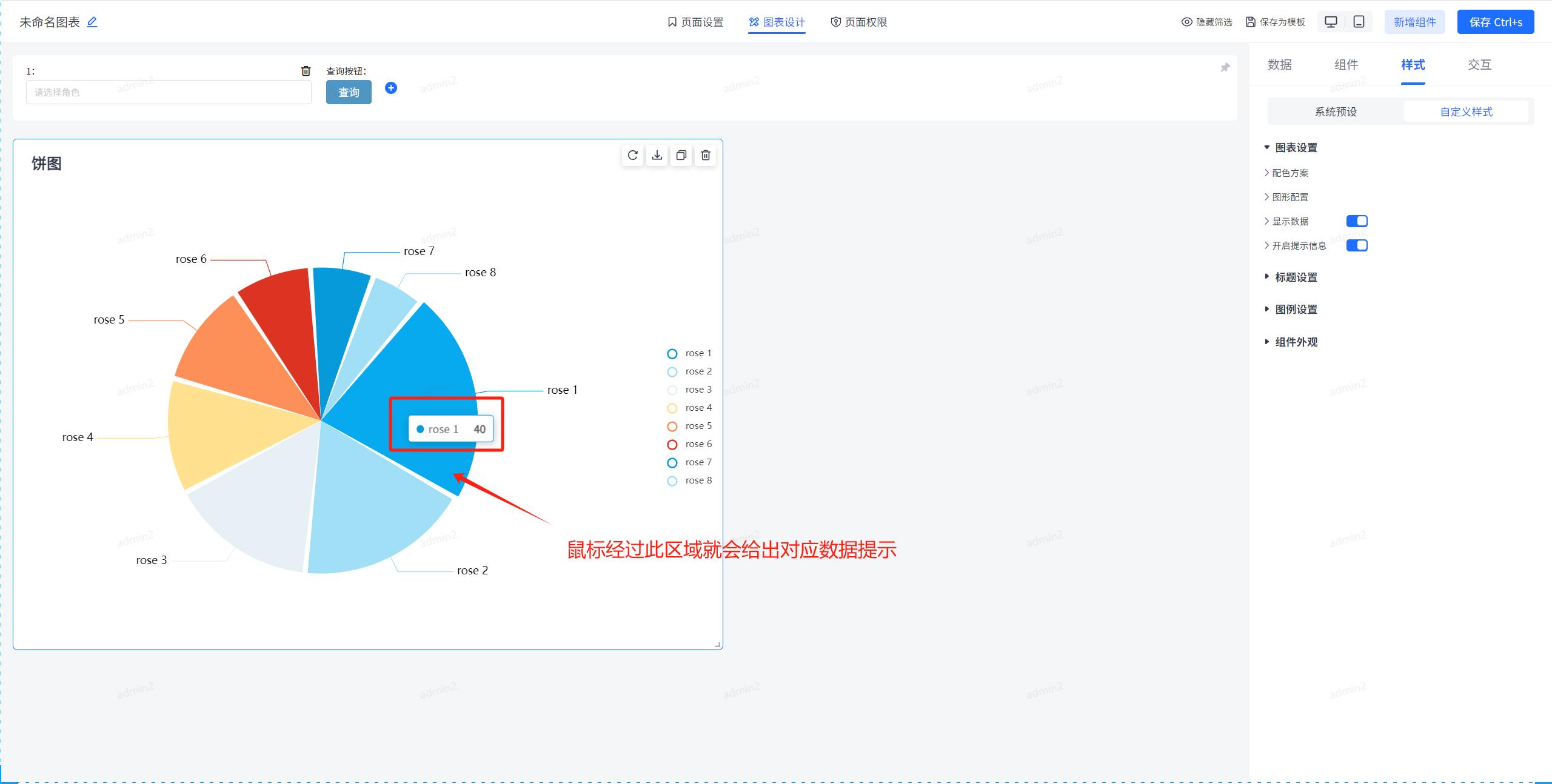
你真的会用饼图吗?JVS-智能BI饼图组件深度解析
在数据可视化的世界里,饼图是我们常见的一种可视化图形。在JVS-智能BI中提供了数据可视化饼图组件,接下来我通过这篇文章详细介绍,从配色方案到图形配置,从显示数据到提示信息,饼图的每一个细节配置。 饼图类图表概述…...

HarmonyOS Next 模拟器安装与探索
HarmonyOS 5 也发布了有一段时间了,不知道大家实际使用的时候有没有发现一些惊喜。当然随着HarmonyOS 5的更新也带来了很多新特性,尤其是 HarmonyOS Next 模拟器。今天,我们就来探索一下这个模拟器,看看它能给我们的开发过程带来什…...

医学机器学习:数据预处理、超参数调优与模型比较的实用分析
摘要 本文介绍了医学中的机器学习,重点阐述了数据预处理、超参数调优和模型比较的技术。在数据预处理方面,包括数据收集与整理、处理缺失值、特征工程等内容,以确保数据质量和可用性。超参数调优对模型性能至关重要,介绍了多种调…...

单片机知识总结(完整)
1、单片机概述 1.1. 单片机的定义与分类 定义: 单片机(Microcontroller Unit,简称MCU)是一种将微处理器、存储器(包括程序存储器和数据存储器)、输入/输出接口和其他必要的功能模块集成在单个芯片上的微型…...

【C++】auto和decltype类型推导关键字
1.C11关键字 auto和decltype是C11引入的关键字,负责类型的推导。所有不同的是: auto可直接用来定义变量,编译器会自动推导出变量的类型。decltype是推导出一个操作数的类型,然后用这个类型再去定义。 2.两者区别 尽管两者都是宏…...

OGRE 3D----3. OGRE绘制自定义模型
在使用OGRE进行开发时,绘制自定义模型是一个常见的需求。本文将介绍如何使用OGRE的ManualObject类来创建和绘制自定义模型。通过ManualObject,开发者可以直接定义顶点、法线、纹理坐标等,从而灵活地构建各种复杂的几何体。 Ogre::ManualObject 是 Ogre3D 引擎中的一个类,用…...

ARM + Linux 开发指南
随想:想写一个系列来讲如何嵌入式开发,然后能形成一个知识体系,帮助那些刚刚做嵌入开发的同学们. 1. ARM Linux从开机到Linux完全启动的流程和代码分析 ARM Linux从开机到完全启动的流程与代码分析 ARM Linux的启动过程主要涉及从设备上电开始,到Linux内核完全启动并进入…...

facebook欧洲户开户条件有哪些又有何优势?
在当今数字营销时代,Facebook广告已成为企业推广产品和服务的重要渠道。而为了更好地利用这一平台,广告主们需要理解不同类型的Facebook广告账户。Facebook广告账户根据其属性可分为多种类型,包括个人广告账户、企业管理(BM&#…...
二刷第三十一天 | 1049. 最后一块石头的重量 II、494. 目标和、*474. 一和零)
算法训练(leetcode)二刷第三十一天 | 1049. 最后一块石头的重量 II、494. 目标和、*474. 一和零
刷题记录 1049. 最后一块石头的重量 II*494. 目标和二维数组滚动数组 *474. 一和零 1049. 最后一块石头的重量 II leetcode题目地址 本题与416. 分割等和子集类似。依旧是01背包问题,本题尽可能将石头分为相等(相近)的两堆,然后…...

软件测试丨Pytest生命周期与数据驱动
Pytest的生命周期概述 Pytest 是一个强大的测试框架,提供了丰富的特性来简化测试执行。它的生命周期包括多个阶段,涉及从准备测试、执行测试到报告结果的完整流程。因此,理解Pytest的生命周期将帮助我们更好地设计和管理测试用例。 开始阶段…...
Figma入门-原型交互
Figma入门-原型交互 前言 在之前的工作中,大家的原型图都是使用 Axure 制作的,印象中 Figma 一直是个专业设计软件。 最近,很多产品朋友告诉我,很多原型图都开始用Figma制作了,并且很多组件都是内置的,对…...

网络安全防范技术
1 实践内容 1.1 安全防范 为了保障"信息安全金三角"的CIA属性、即机密性、完整性、可用性,信息安全领域提出了一系列安全模型。其中动态可适应网络安全模型基于闭环控制理论,典型的有PDR和P^2DR模型。 1.1.1 PDR模型 信息系统的防御机制能抵抗…...

Java - JSR223规范解读_在JVM上实现多语言支持
文章目录 1. 概述2. 核心目标3. 支持的脚本语言4. 主要接口5. 脚本引擎的使用执行JavaScript脚本执行groovy脚本1. Groovy简介2. Groovy脚本示例3. 如何在Java中集成 Groovy4. 集成注意事项 6. 与Java集成7. 常见应用场景8. 优缺点9. 总结 1. 概述 JSR223(Java Spe…...

win10系统部署RAGFLOW+Ollama教程
本篇主要基于linux服务器部署ragflowollama,其他操作系统稍有差异但是大体一样。 一、先决条件 CPU ≥ 4核; RAM ≥ 16 GB; 磁盘 ≥ 50 GB; Docker ≥ 24.0.0 & Docker Compose ≥ v2.26.1。 如果尚未在本地计算机ÿ…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
