vue多页面应用集成时权限处理问题
在多页面应用(MPA)中,权限管理通常会涉及到每个页面的访问控制、身份验证、以及权限校验。以下是几种常见的权限处理方式:
1. 前端路由权限控制
- 原理:虽然是多页面应用,通常每个页面会独立加载和渲染,但你可以在每个页面中使用前端 JavaScript 来校验用户权限。
- 实现方式:通过检查用户的登录状态或权限,决定是否允许访问该页面。如果不符合条件,可以重定向到登录页或展示提示信息。
- 适用场景:适用于需要进行用户权限控制的页面,如管理后台的不同功能模块。
2. 后端权限控制(最常见的做法)
- 原理:对于多页面应用,每个页面通常都会请求后台数据或者获取某些资源。后端可以根据请求的来源和用户身份,进行权限校验。
- 实现方式:
- 在每个请求中,后端可以检查用户的身份和角色,通过 Session 或 Token 等机制验证用户是否具有访问该页面或资源的权限。
- 如果用户权限不够,后端会返回相应的错误信息(如 401 Unauthorized 或 403 Forbidden),前端再根据错误信息进行提示或重定向。
- 适用场景:适用于大多数需要权限控制的应用,特别是在有多个角色(如普通用户、管理员)时,后端能够集中处理权限管理。
3. 统一权限管理
- 原理:通过统一的权限管理系统,进行跨页面的权限校验。这种方式通常涉及到前端和后端的协同工作。
- 实现方式:
- 用户登录时,后端会返回一个包含用户权限信息(如角色、权限标识等)的 Token 或者 Session。
- 前端在请求各个页面时,根据返回的权限信息来控制是否允许访问某些页面。
- 可以通过 Vuex(或类似状态管理工具)统一管理权限信息,确保在多个页面间保持一致性。
- 适用场景:当系统有多个页面需要一致的权限控制,并且每个页面的权限需求可能不同。
4. 基于页面级的权限控制
- 原理:在每个页面加载时,前端根据用户的权限信息判断是否渲染该页面。
- 实现方式:
- 在每个页面的入口处进行权限校验,例如在 Vue 的生命周期钩子中(如
mounted或created)判断当前用户是否有权限访问该页面。 - 若没有权限,前端可以直接跳转到登录页面或者显示“权限不足”提示。
- 在每个页面的入口处进行权限校验,例如在 Vue 的生命周期钩子中(如
- 适用场景:适用于页面结构较为简单,且权限校验主要集中在页面本身的情况。
5. 动态权限控制(懒加载)
- 原理:通过懒加载的方式,动态引入页面及其组件,并根据权限决定是否加载。
- 实现方式:
- 使用 Vue Router 配置懒加载,结合前端权限控制,在路由切换时判断是否允许加载某个页面。
- 如果没有权限,则不加载相关组件,直接跳转到错误页面或登录页。
- 适用场景:适用于大规模应用或页面较多的项目,能够有效减少无权限用户加载不必要的页面和资源。
小结:
- 后端控制 是最常见且最安全的方式,尤其适合多页面应用,因为它可以确保即使用户绕过前端控制,后端也能做最后的权限检查。
- 前端路由控制 适合单页面应用,但也可以在 MPA 中作为补充。
- 统一权限管理 可以实现跨页面权限的集中管理,确保权限控制的一致性。
最终,前后端配合 是处理多页面权限管理的理想方式,后端做最终的权限判断,前端则负责相应的UI渲染和跳转。
相关文章:

vue多页面应用集成时权限处理问题
在多页面应用(MPA)中,权限管理通常会涉及到每个页面的访问控制、身份验证、以及权限校验。以下是几种常见的权限处理方式: 1. 前端路由权限控制 原理:虽然是多页面应用,通常每个页面会独立加载和渲染&…...

Socket编程(TCP/UDP详解)
前言:之前因为做项目和找实习没得空,计算机网络模块并没有写成博客,最近得闲了,把计算机网络模块博客补上。 目录 一,UDP编程 1)创建套接字 2)绑定端口号 3)发送与接收数据 4&…...

qt QConicalGradient详解
1、概述 QConicalGradient是Qt框架中QGradient的一个子类,它用于创建锥形渐变效果。锥形渐变是从一个中心点出发,沿着360度的圆周扩散的颜色渐变。这种渐变通常用于模拟光线旋转、创建彩虹效果或实现其他复杂的颜色过渡。QConicalGradient允许你定义渐变…...

存储过程与自然语言处理逻辑的不同与结合
在现代软件开发中,存储过程与自然语言处理(NLP)逻辑都发挥着重要作用。存储过程是一种在数据库内部运行的预编译程序,通常用于处理与数据相关的任务,例如插入、更新、删除数据以及复杂的查询操作。而自然语言处理&…...

了解Linux —— 理解其中的权限
前言 在了解Linux权限之前,先来探讨我们使用的shell 命令它到底是什么? Linux 是一个操作系统,我们称其为内核(kernel) ,正常情况下,我们一般用户操作并不是去直接使用内核,而是通过kernel 的外壳程序&…...

知识图谱嵌入与因果推理的结合
知识图谱通过节点(实体)和边(关系)来表示现实世界中的信息,但如何将这些信息转化为可进行推理和决策的形式,仍然是一个挑战。 另一方面,因果推理(Causal Inference)作为…...

STM32 PWM波形详细图解
目录 前言 一 PWM介绍 1.1 PWM简介 1.2 STM32F103 PWM介绍 1.3 时钟周期与占空比 二.引脚映像关系 2.1引脚映像与寄存器 2.2 复用功能映像 三. PWM 配置步骤 3.1相关原理图 3.2配置流程 3.2.1 步骤一二: 3.2.2 步骤三: 3.2.3 步骤四五六七: …...

Python Web 开发 FastAPI 入门:从基础架构到框架比较
Python Web 开发 FastAPI 入门:从基础架构到框架比较 目录 🖥️ Web 服务器概述(如 Nginx、Apache)🔗 前后端分离架构详解🔄 HTTP 路由和请求处理机制🧰 Web 框架概述:Django、Fla…...

基于STM32的智能仓库管理系统设计
目录 引言环境准备 硬件准备软件准备智能仓库管理系统基础 控制系统架构功能描述代码实现:实现智能仓库管理系统 4.1 RFID标签读取模块4.2 库存管理模块4.3 数据显示与监控模块4.4 无线通信模块应用场景:智能仓库管理系统优化问题解决方案与优化收尾与总…...

排序算法--堆排序【图文详解】
“留在码头的船才最安全” “但亲爱的,那不是造船的目的。 堆--插入heapInsert 原来有一个大根堆,如图: 现在要新插入一个数字50,进行插入 流程:和父亲相比,如果比父亲大,和父亲交换ÿ…...

FCBP 认证考试要点摘要
理论知识 数据处理与分析:包括数据的收集、清洗、转换、存储等基础操作,以及数据分析方法,如描述性统计分析、相关性分析、数据挖掘算法等的理解和应用 。数据可视化:涉及图表类型的选择与应用,如柱状图、折线图、饼图…...

鸿蒙生态崛起的机遇有什么
鸿蒙生态系统的崛起为各个领域带来了多个机遇,主要体现在以下几个方面: 智能设备的互联互通:鸿蒙系统旨在实现不同设备之间的无缝连接,为物联网(IoT)设备的发展提供了良好的基础。这将推动智能家居、智慧城…...

基础(函数、枚举)错题汇总
枚举默认从0开始,指定后会按顺序赋值 而这个枚举变量X,如果在全局(函数外部)定义,那默认为0,如果在函数内部(局部变量),那就是随机值,必须初始化。 枚举变量…...

【Spark源码分析】规则框架- `analysis`分析阶段使用的规则
analysis分析阶段使用的规则 规则批策略规则说明SubstitutionfixedPointOptimizeUpdateFields该规则优化了 UpdateFields 表达式链,因此看起来更像优化规则。但是,在处理深嵌套模式时,UpdateFields 表达式树可能会非常复杂,导致分…...

mysql--二进制安装编译安装yum安装
二进制安装 创建用户和组 [rootlocalhost ~]# groupadd -r -g 306 mysql [rootlocalhost ~]# useradd -r -g 306 -u 306 -d /data/mysql mysql 创建文件夹并添加所属文件用户和组 [rootlocalhost ~]# mkdir -p /data/mysql [rootlocalhost ~]# chown mysql:mysql /data/mysql …...

《Django 5 By Example》阅读笔记:p339-p358
《Django 5 By Example》学习第12天,p339-p358总结,总计20页。 一、技术总结 1.项目(购物网站) django-admin startproject myshop 虽然这里只是示例,但我觉得这种命名为 myxxx 的习惯非常不好,因为在实际应用中,是…...

鸿蒙修饰符
文章目录 一、引言1.1 什么是修饰符1.2 修饰符在鸿蒙开发中的重要性1.3 修饰符的作用机制 二、UI装饰类修饰符2.1 Styles修饰符2.1.1 基本概念和使用场景2.1.2 使用示例2.1.3 最佳实践 2.2 Extend修饰符2.2.1 基本概念2.2.2 使用示例2.2.3 Extend vs Styles 对比2.2.4 使用建议…...

springboot359智慧草莓基地管理系统(论文+源码)_kaic
毕 业 设 计(论 文) 题目:智慧草莓基地管理系统 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本智慧草莓基地管理系统就…...

单片机位数对性能会产生什么影响?!
单片机的位数是指其处理器核心的位宽,通常以比特(bit)为单位。常见的位数有8位、16位、32位和64位等。 单片机位数越高,处理器能够处理的数据量越大,性能也相应提高。 以下是对单片机位数对性能影响的详细分析&#…...

stm32内部高速晶振打开作为主时钟
首先建议你别这么干,因为内部晶振特别容易受温度等外界影响,很容易卡死或堵死程序 我是因为没画外部晶振电路,所以只能开内部晶振来作为时钟 适用于stm32f103系列 把下面的代码换掉源文件里的时钟源配置 /* 开启HSI 即内部晶振时钟 */RCC…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
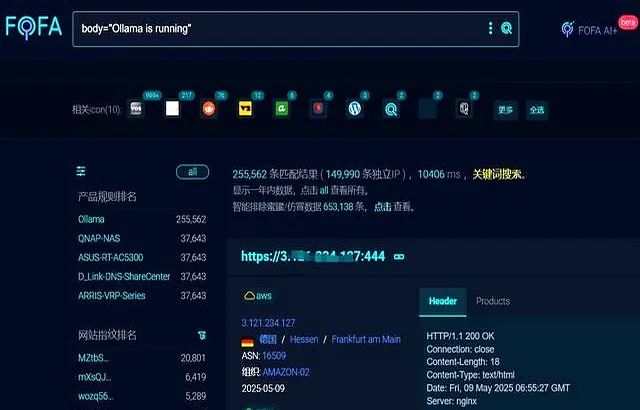
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...
