当前位置： 首页 > news >正文

三除数枚举

news 2026/2/8 11:23:29

给你一个整数 n 。如果 n 恰好有三个正除数 ，返回 true ；否则，返回 false 。

如果存在整数 k ，满足 n = k * m ，那么整数 m 就是 n 的一个 除数 。

输入：n = 4
输出：true
解释：4 有三个除数：1、2 和 4 。
class Solution {public boolean isThree(int n) {int cnt=0;for(int i=1;i*i<=n;i++){if(n%i==0){if(i!=n/i){cnt+=2;}else{cnt+=1;}}}return cnt==3;}
}

相关文章：

三除数枚举

给你一个整数 n 。如果 n 恰好有三个正除数 &#xff0c;返回 true &#xff1b;否则&#xff0c;返回 false 。 如果存在整数 k &#xff0c;满足 n k * m &#xff0c;那么整数 m 就是 n 的一个 除数 。 输入&#xff1a;n 4 输出&#xff1a;true 解释&#xff1a;4 有三…...

编程日记 2024/12/1 18:07:24

【051】基于51单片机温度计【Proteus仿真+Keil程序+报告+原理图】

☆、设计硬件组成&#xff1a;51单片机最小系统DS18B20温度传感器LCD1602液晶显示按键设置蜂鸣器LED灯。 1、本设计采用STC89C51/52、AT89C51/52、AT89S51/52作为主控芯片&#xff1b; 2、采用DS18B20温度传感器测量温度&#xff0c;并且通过LCD1602实时显示温度&#xff1b;…...

编程日记 2024/12/1 18:06:22

[Java]微服务之服务保护

雪崩问题 微服务调用链路中的某个服务故障&#xff0c;引起整个链路中的所有微服务都不可用&#xff0c;这就是雪崩 雪崩问题产生的原因是什么? 微服务相互调用&#xff0c;服务提供者出现故障或阻塞。服务调用者没有做好异常处理&#xff0c;导致自身故障。调用链中的所有服…...

编程日记 2024/12/1 18:05:21

自动驾驶目标检测融合全貌

1、early fusion 早期融合&#xff0c;特点用到几何空间转换3d到2d或者2d到3d的转换&#xff0c;用像素找点云或者用点云找像素。 2、deep fusion 深度融合&#xff0c;也是特征级别融合&#xff0c;也叫多模态融合&#xff0c;如bevfusion范式 3、late fusion 晚融合&#x…...

编程日记 2024/12/1 18:02:10

消息框(Message Box)的测试方法和测试用例

我来帮你了解消息框(Message Box)的测试方法和测试用例的编写。 我已经创建了一个测试用例示例&#xff0c;让我为你解释消息框测试的主要方面&#xff1a; 测试维度&#xff1a; 功能性测试&#xff1a;验证消息框的基本功能是否正常样式测试&#xff1a;确认不同类型消息框…...

编程日记 2024/12/1 17:59:07

Ubuntu 包管理

APT&dpkg 查看已安装包 查看所有已经安装的包 dpkg -l 查找包 apt search <package_name>搜索软件包列表&#xff0c;找到与搜索关键字匹配的包 dpkg与grep结合查找特定的包 dpkg -s <package>&#xff1a;查看某个安装包的详细信息 安装包 apt安装命令 更新…...

编程日记 2024/12/1 17:58:06

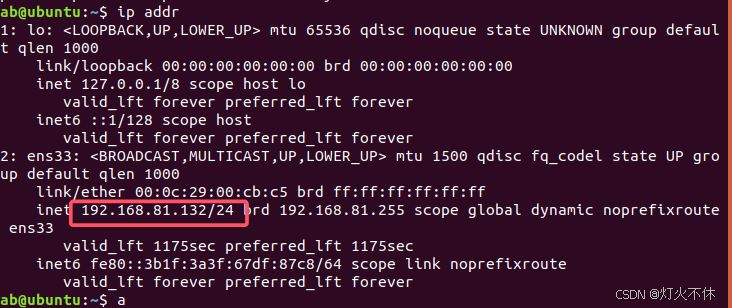
[Ubuntu] linux之Ubuntu18.04的下载及在虚拟机中详细安装过程（附有下载链接）

前言 ubuntu 链接&#xff1a;https://pan.quark.cn/s/283509d0d36e 提取码&#xff1a;dfT1 链接失效&#xff08;可能被官方和谐&#xff09;可评论或私信我重发 下载压缩包后解压 &#xff01;&#xff01;安装路径不要有中文 下载后解压得到.iso文件&#xff0c;不要放在…...

编程日记 2024/12/1 17:57:05

ffmpeg安装(windows)

ffmpeg安装-windows 前言ffmpeg安装路径安装说明 前言 ffmpeg的安装也是开箱即用的,并没有小码哥说的那么难 ffmpeg安装路径 这就下载好了! 安装说明 将上面的bin目录加入到环境变量,然后在cmd中测试一下: C:\Users\12114\Desktop\test\TaskmgrPlayer\x64\Debug>ffmpe…...

编程日记 2024/12/1 17:54:01

服务器数据恢复—raid6阵列硬盘被误重组为raid5阵列的数据恢复案例

服务器存储数据恢复环境&#xff1a; 存储中有一组由12块硬盘组建的RAID6阵列&#xff0c;上层linux操作系统EXT3文件系统&#xff0c;该存储划分3个LUN。 服务器存储故障&分析&#xff1a; 存储中RAID6阵列不可用。为了抢救数据&#xff0c;运维人员使用原始RAID中的部分…...

编程日记 2024/12/1 17:53:00

linux内核编译启动总结

linux kernel 编译 升级汇总 写在前面内核编译获取kernel代码开始前的准备工作 编译过程1\.解压与净化将下载好的linux内核解压至/usr/src 2\. 得到源代码后,将其净化3\. 配置要进行编译的内核4.编译内核. &#xff08;15分钟&#xff09;5.编译模块.方法1:方法2&#xff1a; 6…...

编程日记 2024/12/1 17:50:57

Android Studio的AI工具插件使用介绍

Android Studio的AI工具插件使用介绍 一、前言 Android Studio 的 AI 工具插件具有诸多重要作用&#xff0c;以下是一些常见的方面&#xff1a; 代码生成与自动补全 代码优化与重构 代码解读 学习与知识获取 智能搜索与资源推荐实际使用中可以添加注释&#xff0c;解读某段代…...

编程日记 2024/12/1 17:48:55

本地部署 WireGuard 无需公网 IP 实现异地组网

WireGuard 是一个高性能、极简且易于配置的开源虚拟组网协议。使用路由侠内网穿透使其相互通讯。 第一步&#xff0c;服务端&#xff08;假设为公司电脑&#xff09;和客户端&#xff08;假设为公司外的电脑&#xff09;安装部署 WireGuard 1&#xff0c;点此下载&#xff08;…...

编程日记 2024/12/1 17:42:47

asyncio.ensure_future 与 asyncio.create_task：Python异步编程中的选择

asyncio.ensure_future 与 asyncio.create_task&#xff1a;Python异步编程中的选择 引言asyncio.ensure_futureasyncio.create_task两者的区别参数接受范围任务调度的保证代码可读性 哪个更好&#xff1f;使用asyncio.create_task使用asyncio.ensure_future 结论参考 引言 在…...

编程日记 2024/12/1 17:41:44

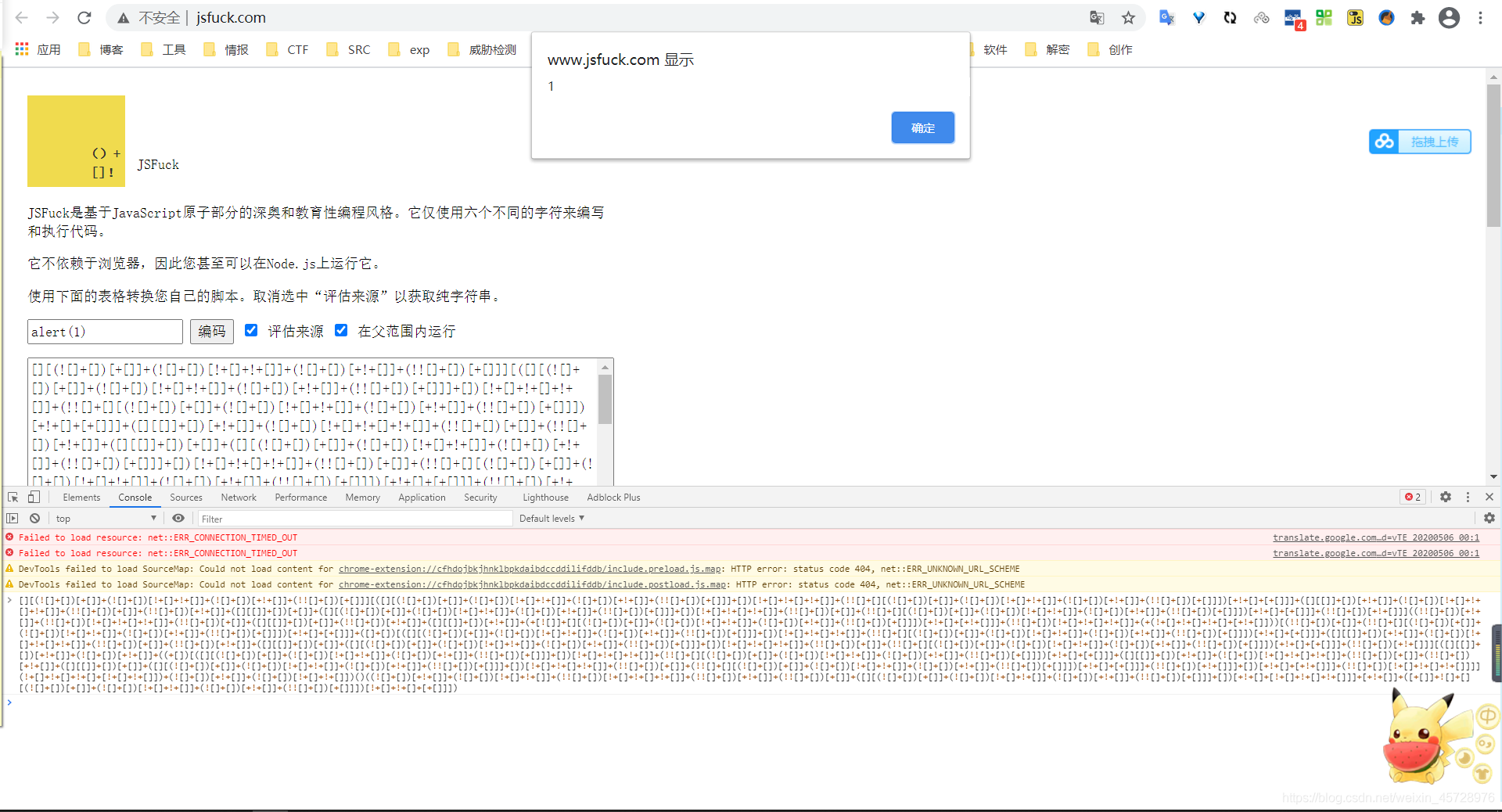
CTF之密码学（密码特征分析）

一.MD5,sha1,HMAC,NTLM 1.MD5&#xff1a;MD5一般由32/16位的数字(0-9)和字母(a-f)组成的字符串 2.sha1&#xff1a;这种加密的密文特征跟MD5差不多&#xff0c;只不过位数是40&#xff08;sha256&#xff1a;64位&#xff1b;sha512:128位&#xff09; 3.HMAC&#xff1a;这…...

编程日记 2024/12/1 17:40:42

JVM调优篇之JVM基础入门AND字节码文件解读

目录 Java程序编译class文件内容常量池附录-访问标识表附录-常量池类型列表 Java程序编译 Java文件通过编译成class文件后&#xff0c;通过JVM虚拟机解释字节码文件转为操作系统执行的二进制码运行。 规范 Java虚拟机有自己的一套规范&#xff0c;遵循这套规范&#xff0c;任…...

编程日记 2024/12/1 17:39:42

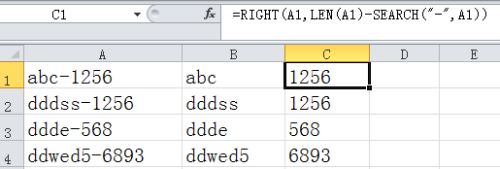
EXCEL截取某一列从第一个字符开始到特定字符结束的字符串到新的一列

使用EXCEL中的公式进行特定截取 假设列A是一组产品的编码&#xff0c;我们需要的数据是“-”之前的字段。 我们需要在B1单元格输入公式“LEFT(A1,SEARCH("-",A1)-1)”然后选中B1至B4单元格&#xff0c;按“CTRLD”向下填充&#xff0c;就可以得出其它几行“-”之前的…...

编程日记 2024/12/1 17:38:41

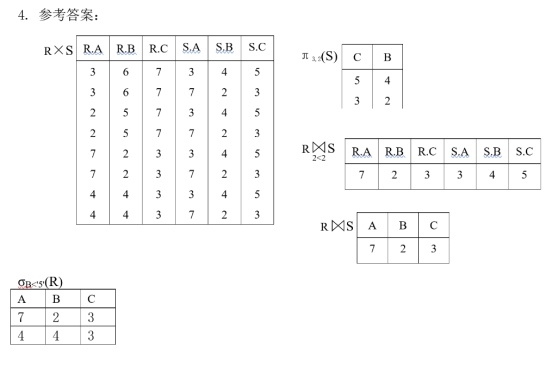
数据库期末复习题库

1. Mysql日志功能有哪些? 记录日常操作和错误信息&#xff0c;以便了解Mysql数据库的运行情况&#xff0c;日常操作&#xff0c;错误信息和进行相关的优化。 2. 数据库有哪些备份方法 完全备份&#xff1a;全部都备份一遍表备份&#xff1a;只提取数据库中的数据&#xff0…...

编程日记 2024/12/1 17:36:38

私有库gitea安装

一 gitea是什么 Gitea是一款自助Git服务&#xff0c;简单来说&#xff0c;就是可以一个私有的github。 搭建很容易。 Gitea依赖于Git。 类似Gitea的还有GitHub、Gitee、GitLab等。 以下是安装步骤。 二 安装sqilite 参考&#xff1a; 在windows上安装sqlite 三 安装git…...

编程日记 2024/12/1 17:35:36

关于最近win11不能使用ie，而不能使用考试客户端的解决方法

弄ie的那个我感觉是非常难的&#xff0c;所以我的是另一种的方法 下载360浏览器&#xff08;不是360全家桶&#xff09;360安全浏览器-全面保护上网安全&#xff0c;4亿用户共同选择&#xff08;上面的是官网&#xff0c;不要下载错了&#xff0c;还有安装界面注意不要勾选一下…...

编程日记 2024/12/1 17:33:33

深度学习之Mask-R-CNN

1.1 Mask-RCNN 的网络结构示意图 其中黑色部分为原来的Faster-RCNN&#xff0c;红色部分为在Faster网络上的修改&#xff1a;    1&#xff09;将ROI Pooling层替换成了ROIAlign&#xff1b;    2&#xff09;添加并列的FCN层&#xff08;Mask层&#xff09;&#xff1b;  …...

编程日记 2024/12/1 17:32:33

铭豹扩展坞 USB转网口 突然无法识别解决方法

当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...

编程新知 2026/2/8 4:37:22

【磁盘】每天掌握一个Linux命令 - iostat

目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat&#xff08;I/O Statistics&#xff09;是Linux系统下用于监视系统输入输出设备和CPU使…...

编程新知 2025/9/30 16:39:11

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

PL0语法，分析器实现！

简介 PL/0 是一种简单的编程语言，通常用于教学编译原理。它的语法结构清晰，功能包括常量定义、变量声明、过程（子程序）定义以及基本的控制结构（如条件语句和循环语句）。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言，由 Niklaus Wirth 设计，用于展示编译原理的核…...

编程新知 2026/1/29 17:06:33

鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/

使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题&#xff1a;docker pull 失败 网络不同&#xff0c;需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

编程新知 2025/12/31 6:28:08

企业如何增强终端安全？

在数字化转型加速的今天&#xff0c;企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机&#xff0c;到工厂里的物联网设备、智能传感器&#xff0c;这些终端构成了企业与外部世界连接的 “神经末梢”。然而&#xff0c;随着远程办公的常态化和设备接入的爆炸式…...

编程新知 2026/1/29 9:14:58

关键领域软件测试的突围之路：如何破解安全与效率的平衡难题

在数字化浪潮席卷全球的今天&#xff0c;软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件&#xff0c;这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下&#xff0c;实现高效测试与快速迭代&#xff1f;这一命题正考验着…...

编程新知 2026/1/27 13:20:11

Java 二维码

Java 二维码 **技术&#xff1a;**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

编程新知 2025/9/6 16:22:45

PAN/FPN

import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

编程新知 2025/10/20 4:39:36

AI+无人机如何守护濒危物种？YOLOv8实现95%精准识别

【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而&#xff0c;传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案&#xff0c;能够实现大范围覆盖并远程采集数据。尽管具备这些优势&#xf…...

编程新知 2026/1/26 12:50:00