《数字图像处理基础》学习07-图像几何变换之最近邻插值法放大图像
目录
一,概念
二,题目及matlab实现
1,解题思路
2,matlab实现
1)matlab思路
2)完整代码
三,放大图像及matlab实现
一,概念
通过上一篇,我已经学习了使用最邻近插值法来缩小图像
《数字图像处理基础》学习06-图像几何变换之最邻近插值法缩小图像-CSDN博客
依旧需要使用到如下公式(因为在上一篇文章已经学习过,所以这里不赘诉):
和使用最邻近插值法缩小图像不同。如果要使用最邻近插值法放大图像,则需要将原始图像的每行 和每列
都乘上对应的放大倍数
,得到原始图像中像素值的像素点(即像素值的坐标)的最大分布。
例如,有一个原始图像矩阵 尺寸大小为
,将其放大
倍 ,可得到尺寸大小为
的放大图像矩阵
。
接着将原始图像矩阵的第一个元素的坐标(),分别乘上对应的放大倍数(如果是非等比例放大则k有两个不同的取值:
和
),此时原始图像第
行第
列的像素值会跑到放大图像的第
行第
列,并且放大图像从
行 及
列之间的像素值都用原始图像的第
行第
列的像素值来填充。如果放大倍数是小数,则计算后按照四舍五入法取值。接下来可以通过题目来加深使用最邻近插值法放大图像的具体过程。
二,题目及matlab实现
下面是一个简单的例子。给出一个原始图像矩阵 大小为
将其放大:
- 高(行)放大的倍数为
- 宽(列)的放大倍数为
求对其放大后的图像矩阵 。
% 可以试着先自己做一做,如果解出来的g如下:
则思路正确,直接用自己的思路编写matlab程序去处理读取的图像,下面的解题思路可以选择跳过。
1,解题思路
从之前的概念中就已经可以用手算出g。
例如:
-
首先根据放大原始图像
的行列倍数创建一个放大后的图像矩阵

-
原始图像
第
行第
列的像素值会跑到放大图像
的第
行第
列,并且放大图像
从
行 及
列之间的像素值都用原始图像
的第
行第
列的像素值来填充,如下👇

-
原始图像
第
行第
列的像素值会跑到放大图像
的第
行第
列,并且放大图像
从
行 及
列之间的像素值都用原始图像的第
行第
列的像素值来填充,如下👇

可以看到,填充时的列起始位置跟上一次的填充的列结束位置有关,例如,上一次的填充在
结束,那么这一次的填充从
开始,一直填充到
为止。原始图像
第
行第
列的像素值操作一样。

-
原始图像
第
行第
列的像素值会跑到放大图像
的第
行第
列,并且放大图像
从
行 及
列之间的像素值都用原始图像的第
行第
列的像素值来填充,如下👇

可以看到,填充时的行起始位置跟上一次的填充的行结束位置有关,例如,上一次的填充在
结束,那么这一次的填充从
开始,一直填充到
为止。
-
后面的操作类似,这里不赘诉,最后得到的放大矩阵g如下👇

2,matlab实现
1)matlab思路
在通过解题思路中,可以看到在填充过程中,不变的是原始图像矩阵中的每一个像素放大后的对应像素点(像素的坐标,i,j),因此, 读取图像形成矩阵 和产生全零的放大矩阵
之后,可以先将原始图像矩阵的每一行每一列放大后在放大图像矩阵中的位置分别用数组存储起来:
- 数组
,存储原始图像矩阵的每一行放大后在放大图像矩阵中的最大位置。
- 数组
,存储原始图像矩阵的每一列放大后在放大图像矩阵中的最大位置。
虽然matlab在声明一维数组时可以不用声明一维数组的类型及指定一维数组的大小,但至少得有一个数组元素。例如, % 数组ia中有一个元素 1
于是,需要在matlab中写下如下语句,创建数组ia和数组ja:
ia=[1]; %之所以给定元素1,是因为在matlab中索引是从1开始,不管是遍历原始图像矩阵的行列,还是填充放大图像矩阵的行列,它们的第一个元素的行都是从1开始,列也是从1开始,即第一个元素的坐标为(1,1)
ja=[1];
for i=1:h % 原始图像的高(行数)ia(end+1)=round(i*k1)+1; % 创建存储原始图像矩阵的每一行放大后在放大图像矩阵中的最大位置的数组
% ia(end+1)可以在数组ia的已有元素末尾添加新的数组元素
end
for j=1:w % 原始图像的宽(列数)ja(end+1)=round(j*k2)+1; % 创建存储原始图像矩阵的每一列放大后在放大图像矩阵中的最大位置的数组
end上述创建数组的代码也可以简化成如下形式(如果后面嵌套多的话就需要用到简化)👇:
ia = round((0:h) * k1) + 1;
% 之所以要加1,是因为原始图像矩阵在当前行或列在放大时,得到的就是在放大图像矩阵中的最大位置
% 而下一个填充的行或列的填充位置需要上一个位置加1,为了方便起见,都将结果加1,之后遍历的时候再进行相应的处理。
ja = round((0:w) * k2) + 1;接下来就开始遍历原始图像矩阵,为了后期让这个代码也可以应用到图像处理中,因此,还需要加上用来遍历像素值的颜色通道变量 (在获取原始图像矩阵
时,获取到该图像的颜色通道数
,之后在创建放大图像矩阵
时,也需要传入颜色通道数
)。像给出的题目中的图像矩阵 f 很简单,所以也不包含颜色,不是彩色图像,因此,是灰度图像,它的颜色通道数
。
我通过最邻近插值法的相关概念和解题思路,可以知道,放大图像被填充的像素值与上一次的填充有关,而相关的坐标已经用数组 ia 和 ja 存储:
- 例如:原始图像
只有两行,所产生的数组ia只有3个元素:1;1*k1+1;2*k1+1。数组ja也只有三个元素:1;1*k2+1;2*k2+1。
- 如果想要遍历整个数组ia,只需要循环两次就行,因为通过观察,可以发现遍历数组ia 和 ja 的循环次数分别与原始图像矩阵的行数和列数一样。
- 我一般喜欢按照将变量名命名成与之相关的其它变量。例如,如果想要遍历原始图像
的行
,我就会用
表示原始图像
的每一行。
表示原始图像
的每一列。
- 在填充的过程中,放大图像
的像素值的行
和列
都会变化:起始位置对应数组的当前元素,结束位置为对应数组的下一个元素的值减一。
【可以自己选择带入个别的值来验证】
根据上述写出的代码如下👇
for c=1:dimfor fi=1:hfor fj=1:wfor gi=ia(fi):ia(fi+1)-1for gj=ja(fj):ja(fj+1)-1g(gi,gj,c)=f(i,j,c);endendendend
end由于嵌套过多,会导致运算出现问题,因此,可以将最里面的两个循环语句简化,如下:
for c = 1:dimfor fi = 1:hfor fj = 1:wg(ia(fi):(ia(fi+1)-1), ja(fj):(ja(fj+1)-1), c) = f(fi,fj,c);endend
end2)完整代码
clear all; clear; clc;% 清空工作空间
f = [1, 4, 7; 2, 5, 8; 3, 6, 9];
[h,w,dim] = size(f);
k1 = 1.2;
k2 = 2.5;
nh = round(k1 * h);
nw = round(k2 * w);
g = zeros(nh, nw, dim, 'uint8');
ia = round((0:h) * k1) + 1;
ja = round((0:w) * k2) + 1;
for c = 1:dimfor fi = 1:hfor fj = 1:wg(ia(fi):(ia(fi+1)-1), ja(fj):(ja(fj+1)-1), c) = f(fi,fj,c);endend
end
% 显示结果
disp('输入矩阵 f:');
disp(f);
disp('输出矩阵 g:');
disp(g);运行后的结果和之前通过做题得到的结果一样:
三,放大图像及matlab实现

clear all; clear; clc; % 清空工作空间
f = imread('01.jpg');
[h,w,dim] = size(f);
k1 = 1.2;
k2 = 2.5;
nh = round(k1 * h);
nw = round(k2 * w);
g = zeros(nh, nw, dim, 'uint8');
ia = round((0:h) * k1) + 1;
ja = round((0:w) * k2) + 1;for c = 1:dimfor fi = 1:hfor fj = 1:wfv = f(fi, fj, c);g(ia(fi):(ia(fi+1)-1), ja(fj):(ja(fj+1)-1), c) = fv;endend
end
disp('图像处理完成。');
figure;
subplot(121);
imshow(f);
title(['分辨率为:', num2str(size(f, 1)), '×', num2str(size(f, 2)), '的原图像']);
subplot(122);
imshow(g);
title(['分辨率为:', num2str(size(g, 1)), '×', num2str(size(g, 2)), '的放大图像']);
imwrite(g, 'D:\myMatlab\img\01near_increase.jpg');如果想要等比例放大图像,可以将放大倍数k1和k2设置一样的数值。如下就是等比例放大6倍的图像👇

一般来说,很少用最邻近插值法来放大图像,基本使用的时双线性插值法来放大图像,之所以我要写这篇文章,主要是因为刚刚好学了,想着雁过留痕,就将自己的学习记录下来,往后还可以再看看。
如果有兴趣的话,可以关注专栏,之后会持续更新有关数字图像处理相关的内容及知识点。
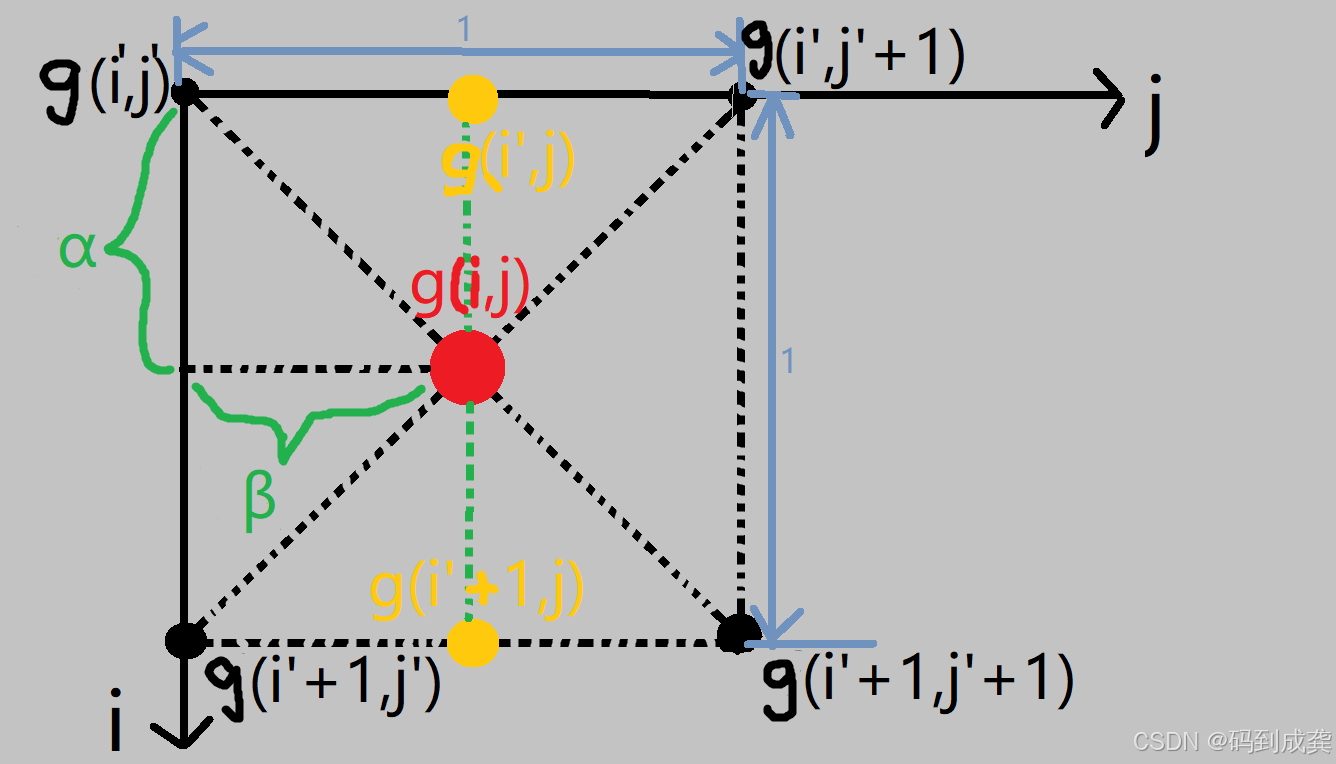
如下就是双线性插值法的核心图:通过邻近四点,求得缩放图像的 像素值 👇
如果对文章的内容有问题或者是有更好的建议请在评论区留言或者是私信我,回复时间不超过一天。
相关文章:

《数字图像处理基础》学习07-图像几何变换之最近邻插值法放大图像
目录 一,概念 二,题目及matlab实现 1,解题思路 2,matlab实现 1)matlab思路 2)完整代码 三,放大图像及matlab实现 一,概念 通过上一篇,我已经学习了使用最邻近插…...

pip安装库时报错(请求超时)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

XPath表达式详解及其在Web开发中的应用
XPath(XML Path Language)是一种强大的查询语言,用于在XML文档中选择节点。由于HTML可以被视为一种特殊的XML,因此XPath同样适用于HTML文档。XPath允许开发者通过元素的层级结构和属性来选择节点或节点集合,这使得它成…...

Qt中Socket网络编程
文章目录 Qt中Socket网络编程服务器端客户端 Qt中Socket网络编程 这里就拿b站上爱编程的小丙的demo来做总结吧,首先要感谢成功带我入门的人:爱编程的小丙和程序员长风,这两个人是讲Socket编程我听懂的课555,接下来就总结一下Qt中…...

【05】Selenium+Python 两种文件上传方式(AutoIt)
上传文件的两种方式 一、input标签上传文件 可以用send_keys方法直接上传文件 示例代码 input标签上传文件import time from selenium import webdriver from chromedriver_py import binary_path # this will get you the path variable from selenium.webdriver.common.by i…...

Python网络编程
网络编程 Socket(套接字) socket 位于 网络协议中的 数据传输层、 该层 主要 可以通过 UDP 或者 TCP协议 实现 数据的传输 TCP 协议 VS UDP协议 tcp : 是一个 可靠的 ,面向 连接的协议。 数据在网络传输中 是安全的,不易丢失的。 TCP连接 在建立的时候&…...

openssl生成ca证书
常见CA文件夹 1、生成CA钥匙 openssl genrsa -out ./private/cakey.pem 2、生成CA自签名 openssl req -new -x509 -key ./private/cakey.pem -out ./cacert.crt -days 3650 3、生成http服务器私钥 openssl genrsa -out ./data/frontt.project.com.key 2048 4、CA给http服务器…...

Oracle RAC 环境下数据文件误建在本地目录的处理过程
问题描述 在 Oracle RAC 环境中,有时会误将数据文件创建在本地目录,导致其他节点无法访问该数据文件,从而报出 ORA-01157 和 ORA-01110 错误。 问题分析 错误日志 Mon Nov 16 19:02:38 2021 Errors in file /u01/app/oracle/diag/rdbms/orc…...

新质驱动·科东软件受邀出席2024智能网联+低空经济暨第二届湾区汽车T9+N闭门会议
为推进广东省加快发展新质生产力,贯彻落实“百县千镇万村高质量发展工程”,推动韶关市新丰县智能网联新能源汽车、低空经济与数字技术的创新与发展,充分发挥湾区汽车产业链头部企业的带动作用。韶关市指导、珠三角湾区智能网联新能源汽车产业…...

windows11 使用体验记录
好的地方: UI上字体风格貌似更好看了,文件夹增加了多个标签,类似于浏览器既可以打开多个窗口,也可以在同一个窗口中打开多个标签页 不好的地方: 桌面右下角点击日期时间,显示日期,时间呢&…...

202页MES项目需求方案深入解读,学习MES系统设计规划
202页MES项目需求方案深入解读,学习MES系统设计规划 MES项目需求方案旨在实现制造执行、效率提升、精细化管理等多个方面的功能。整体结构分为七大部分,包括制造执行、效率、精细化、品质在线、设备、用户思想和数据互联。制造执行部分关注订单、品质数据…...

前端css实例
前端css实例 一、带条纹的表格 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>条纹样式的表格<…...

YOLO的框架及版本迭代
YOLO(You Only Look Once)是一种非常流行的实时目标检测算法,其特点是将目标检测任务转换为一个回归问题,通过一次前向传播就可以同时完成目标的分类和定位。以下是YOLO框架的整体架构和工作原理: 一、YOLO的基本框架…...
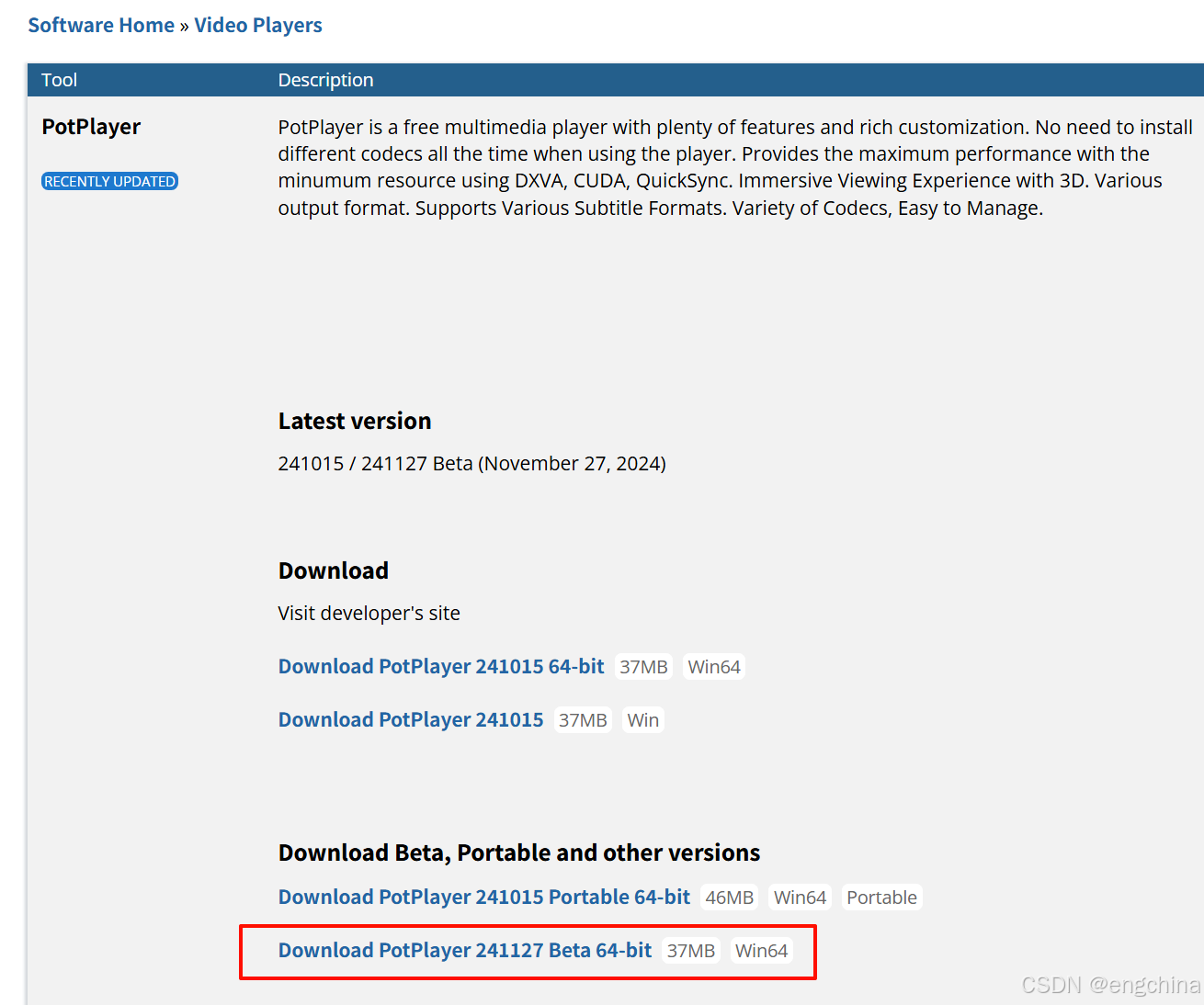
PotPlayer 最新版本支持使用 Whisper 自动识别语音生成字幕
PotPlayer 最新版本支持使用 Whisper 自动识别语音生成字幕 设置使用下载地址 设置 使用 下载地址 https://www.videohelp.com/software/PotPlayer...
)
JavaScript零基础入门速通(中)
目录 1. 函数 1.1 函数声明 1.2 返回值 1.3 匿名函数 1.4 箭头函数 2. 对象 2.1 创建对象 2.2 访问和修改对象的属性 2.3 对象方法 3. 数组 3.1 创建数组 3.2 数组方法 3.3 遍历数组 4. 作用域 4.1 全局作用域 4.2 局部作用域 4.3 块级作用域 5. 事件处理 5…...

【Yarn Bug】 yarn 安装依赖出现的网络连接问题
最近,在初始化 Ant Design Pro 前端脚手架过程中,使用 yarn 安装依赖时遇到了网络连接问题,具体错误信息提示为 info There appears to be trouble with your network connection. Retrying...。通过百度查询,得知出现这种问题的原…...

字节青训Marscode_5:寻找最大葫芦——最新题解
步骤1:问题定义与分析 输入条件: 整数n:牌的数量整数max:葫芦牌面值之和的上限数组array:n张牌的牌面值 输出条件: 两个整数组成的数组[a,b]: a表示三张相同牌的牌面值b表示两张相同牌的牌面值如…...

MySQL —— MySQL 程序
目录 前言 一、MySQL 程序简介 二、mysqld -- MySQL 服务器 三、mysql -- MySQL 客户端 1. mysql 客户端简介 2. mysql 客户端选项 (1)指定选项的方式 (2)mysql 客户端命令常用选项 (3)在命令行中使…...

LLamafactory API部署与使用异步方式 API 调用优化大模型推理效率
文章目录 背景介绍第三方大模型API 介绍LLamafactory 部署API大模型 API 调用工具类项目开源 背景介绍 第三方大模型API 目前,市面上有许多第三方大模型 API 服务提供商,通过 API 接口向用户提供多样化的服务。这些平台不仅能提供更多类别和类型的模型…...

不玩PS抠图了,改玩Python抠图
网上找了两个苏轼的印章图片: 把这两个印章抠出来的话,对于不少PS高手来说是相当容易,但是要去掉其中的水印,可能要用仿制图章慢慢描绘,图章的边缘也要慢慢勾画或者用通道抠图之类来处理,而且印章的红色也不…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
