【力扣】2094.找出3为偶数
思路
方法一:使用Set集合
1.首先是三层for循环,遍历,并且遇到不满足的情况,便跳过,继续计算。不如前导为0,以及遍历同一个数组下标的情况 2.使用Set集合来确保答案是唯一的,使用桶来标记也是可以的 3.但是使用了Set集合就要将其转换为数组来返回,因为题目要求返回的是数组,并且也要用到一些Set的方法。
class Solution {public int[] findEvenNumbers(int[] digits) {Set<Integer> resultSet = new HashSet<>();int len = digits.length;for (int i = 0; i < len; i++) {if (digits[i] == 0) continue;for (int j = 0; j < len; j++) {if (j == i) continue;for (int k = 0; k < len; k++) {if (k == i || k == j || digits[k] % 2 != 0) continue;resultSet.add(digits[i] * 100 + digits[j] * 10 + digits[k]);}}}//将Set集合转为ListList<Integer> res = new ArrayList<>(resultSet);Collections.sort(res);int[] resultArray = new int[res.size()];for (int i = 0; i < res.size(); i++) {resultArray[i] = res.get(i);}return resultArray;}}通过情况:

方法二:使用数字标记
1.因为是三位的偶数,所以只要大小为1k的数字即可
2.前面的判断条件都是一样的,不满足的情况就跳过
3.不同的是,因为不是Set集合,没有办法自动去重,但是好在范围只在100~999的偶数即可,所以i+=2
4.因为不知道有多少满足条件的数字,所以仍然使用List集合,并且在得到结果后再转为数组。
class Solution {public int[] findEvenNumbers(int[] digits) {int[] res=new int[1000];int len = digits.length;for (int i = 0; i < len; i++) {if (digits[i] == 0) continue;for (int j = 0; j < len; j++) {if (j == i) continue;for (int k = 0; k < len; k++) {if (k == i || k == j || digits[k] % 2 != 0||res[digits[i] * 100 + digits[j] * 10 + digits[k]]!=0) continue;res[digits[i] * 100 + digits[j] * 10 + digits[k]]++;}}}List<Integer> resultList=new ArrayList<>();for (int i = 100; i <999 ; i+=2) {if(res[i]!=0)resultList.add(i);}int[] resultArray = new int[resultList.size()];for (int i = 0; i < resultList.size(); i++) {resultArray[i] = resultList.get(i);}return resultArray;}}通过情况:

方法三:直接对0~9出现的数字进行标记
1.既然方法二用的数组标记,是对100-999中的进行标记。那么还有没有更简便的方法呢?
2.直接对0-9的数字进行标记,出现了,则++
3.并且i从1开始,这样就可以避免前导0的问题,k+=2,就能确保找到的都是偶数
4.计算的时候暂时减去使用的次数,这是为了防止,后面的位数进行多次的使用,如果次数不足的情况下。计算完成后再加回来,因为便利和出现的次数无关,遍历是从0~9开始的遍历,如果数字不存在,则会跳过。
5.最后仍是将List转化为 int[ ],返回
class Solution {public int[] findEvenNumbers(int[] digits) {// 创建一个长度为10的数组cnt来记录digits中各个数字(0-9)出现的次数int[] cnt = new int[10];for (int d : digits) {cnt[d]++; // 统计每个数字出现的次数}// 创建一个列表list用于存储找到的所有符合条件的三位偶数List<Integer> list = new ArrayList<>();// 外层循环遍历可能的百位数字i (从1到9,避免前导零)for (int i = 1; i < 10; i++) {if (cnt[i] == 0) continue; // 如果该数字不存在于digits中,则跳过// 暂时减少百位数字i的计数,表示它已经被使用cnt[i]--;// 中间层循环遍历可能的十位数字j (从0到9)for (int j = 0; j < 10; j++) {if (cnt[j] == 0) continue; // 如果该数字不存在于digits中,则跳过// 暂时减少十位数字j的计数,表示它已经被使用cnt[j]--;// 内层循环遍历可能的个位数字k (从0到9,步长为2,确保是偶数)for (int k = 0; k < 10; k += 2) {if (cnt[k] > 0) { // 如果该偶数存在于digits中// 构建三位数并添加到结果列表中list.add(100 * i + 10 * j + k);}}// 恢复十位数字j的计数cnt[j]++;}// 恢复百位数字i的计数cnt[i]++;}// 将结果列表转换为数组int[] nums = new int[list.size()];for (int i = 0; i < list.size(); i++) {nums[i] = list.get(i);}// 返回结果数组return nums;}}相关文章:

【力扣】2094.找出3为偶数
思路 方法一:使用Set集合 1.首先是三层for循环,遍历,并且遇到不满足的情况,便跳过,继续计算。不如前导为0,以及遍历同一个数组下标的情况 2.使用Set集合来确保答案是唯一的,使用桶来标记也是可以的 3.但是…...

利用红黑树封装map,和set,实现主要功能
如果不知道红黑树是什么的时候可以去看看这个红黑树 思路 首先我们可以把封装分为两个层面理解,上层代码就是set,和map,底层就是红黑树 就相当于根据红黑树上面套了两个map,set的壳子,像下面这张图一样 对于map和set,map里面存…...

网络(TCP)
目录 TCP socket API 详解 套接字有哪些类型?socket有哪些类型? 图解TCP四次握手断开连接 图解TCP数据报结构以及三次握手(非常详细) socket缓冲区以及阻塞模式详解 再谈UDP和TCP bind(): 我们的程序中对myaddr参数是这样…...

CSS 选择器的优先级
一、基本概念 CSS 选择器的优先级决定了在样式冲突时,哪个样式规则将被应用到 HTML 元素上。通过理解 CSS 选择器的优先级,可以更好地控制网页元素的样式,避免样式冲突。 二、优先级计算规则 1. 内联样式 内联样式具有最高的优先级。 &l…...

留学生数学辅导作业随机过程高等线性代数概率论微积分优化统计
针对留学生数学辅导作业中的随机过程、高等线性代数、概率论、微积分、优化以及统计等科目,以下是一些详细的辅导建议和资源概述: 一、随机过程 概念理解: 随机过程是研究随机现象随时间演变的数学分支。它涉及概率论和数理统计的知识&#…...

移动机器人课程建图实验-ROSbug汇总
问题1描述 $ rosrun robot_state_publisher robot_state_publisher [ERROR] [1733131886.474757207]: [registerPublisher] Failed to contact master at [localhost:11311]. Retrying...解决方案 这个错误信息表明 robot_state_publisher 节点无法联系到 ROS master。通常&…...

小家电出海,沃丰科技助力保障售后服务的及时性与高效性
随着全球化步伐的加快,小家电行业也逐渐迈向国际市场,面向全球消费者提供服务。然而,跨国界的销售和服务挑战也随之而来,尤其是售后服务的及时性与高效性成为了企业亟需解决的问题。沃丰科技凭借其全渠道在线客服、工单系统和视频…...

vscode 如何支持点击跳转函数,以C++为例,Python等其它编程语言同理,Visual Studio Code。
VScode(Visual Studio Code)按住Ctrl鼠标左键,没法跳转到对应的函数怎么办。 如下图所示 1、点击有四个小方块的图标 2、输入C(如果你的编程语言是C,其它的就输其它的) 3、找到C Extension(其它编程语言࿰…...

创建子类对象时,会创建父类对象吗
一、查询网上的结论: 创建子类对象时, 会先调用子类构造方法对子类对象进行初始化,子类构造方法的第一行又会调用父类构造方法对父类进行初始化(不会创建父类对象, 但是会在子类对象的内存空间中开辟一块被包含的内存空间存储父类…...
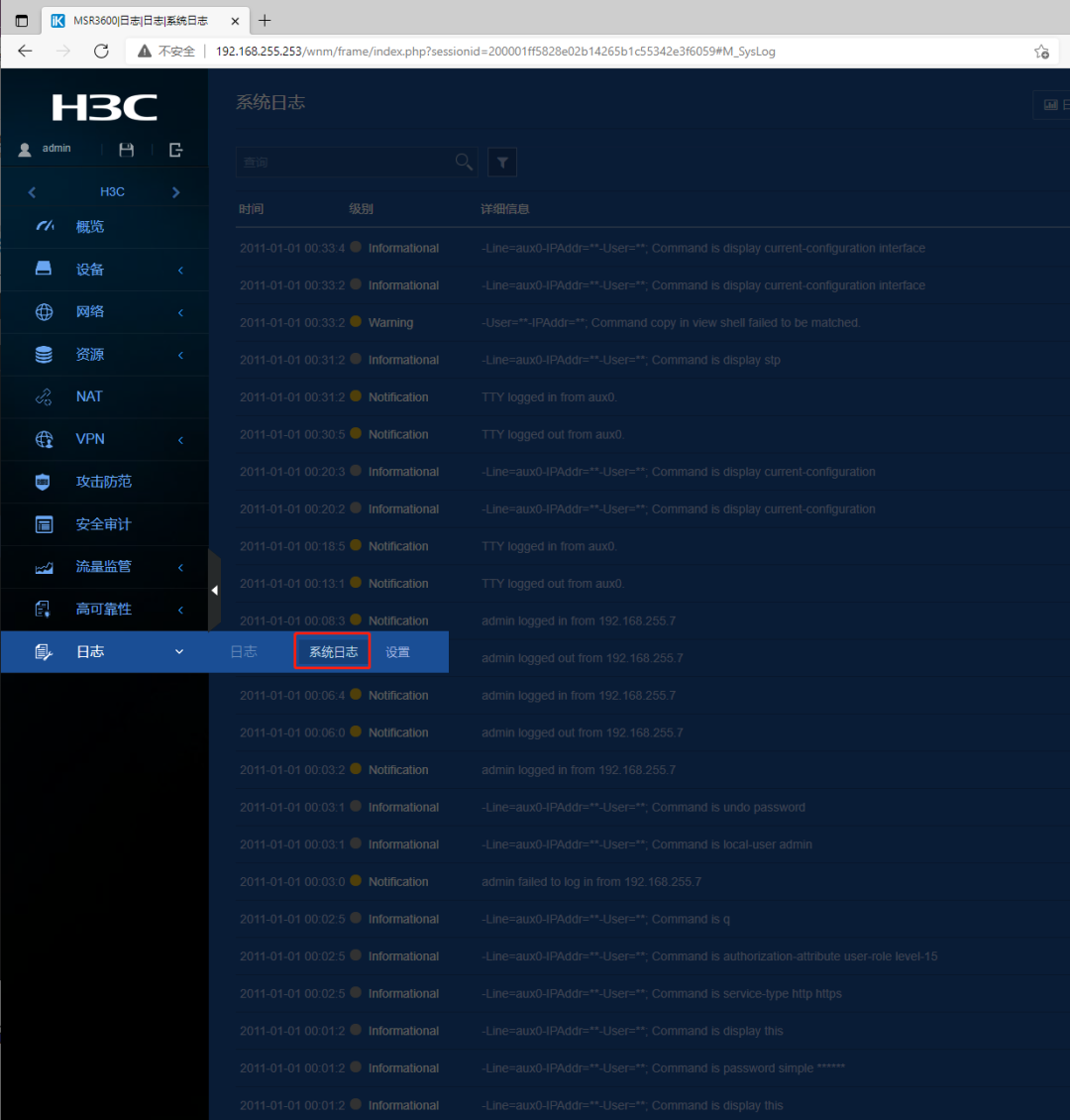
华为、华三交换机纯Web下如何创关键VLANIF、操作STP参数
华为交换机WEB操作 使用的是真机S5735,目前主流的版本都适用(V1R5~V2R1的就不在列了,版本太老了,界面完全不一样,这里调试线接的console口,电脑的网络接在ETH口) 「模拟器、工具合集」复制整段内…...

MongoDB分片集群架构实战
分片集群架构 分片简介 分片(shard)是指在将数据进行水平切分之后,将其存储到多个不同的服务器节点上的一种扩展方式。分片在概念上非常类似于应用开发中的“水平分表”。不同的点在于,MongoDB本身就自带了分片管理的能力&#…...

架构 | 调优 - [zookeeper]
INDEX 0 实际使用的 zoo.cfg1 基础知识1.1 官网文档1.2 日志相关配置1.3 tick 时间 0 实际使用的 zoo.cfg ### 时间配置 ### 一个tick(滴答)的毫秒数,时间单位,可以认为是心跳时间 tickTime2000 ### follower 连接 leader 并与之…...

威联通-004 安装photoview相册应用Docker镜像
文章目录 前言准备MariaDB 10phpMyAdminphotoview 安装步骤1.安装MariaDB 10和phpMyAdmin2.初始安装MariaDB 103.进入phpMyAdmin添加账户4.手动下载photoview的Docker库注意:安装 phpMyAdmin 报错5.配置photoview6.容器安装成功之后进入photoview注意:这…...

Github clone 的时候出现Error in the HTTP2 framing layer错误
解决方案 github鉴权认证,打开gitbash,并输入 ssh-keygen -t rsa -C "emailicjs.cc" 执行后会在 .ssh 目录生产两个文件:id_rsa(私有密钥)和id_rsa.pub(公开密钥) 直接默认回车执行…...

SpringBoot中@Import和@ImportResource和@PropertySource
1. Import Import注解是引入java类: 导入Configuration注解的配置类(4.2版本之前只可以导入配置类,4.2版本之后也可以导入普通类)导入ImportSelector的实现类导入ImportBeanDefinitionRegistrar的实现类 SpringBootApplication…...

OpenCV 简介与安装方法
大家好啊,我是董董灿。 如果你在做计算机视觉相关的工作,肯定少不了使用 OpenCV 库。 在《计算机视觉专栏》的传统计算机视觉部分,我曾经使用 OpenCV 进行了很多图像的处理,比如边缘检测。 刚好最近在整理一份文稿,…...

pycharm基本库安装的几种方法
1、pycharm基本库安装的几种方法 1)一次性设置下载源 cmd窗口(管理员方式).输入以下命令: pip config set global.index-url http://pypi.tuna.tsinghua.edu.cn/simple pip config set global.trusted-host pypi.tuna.tsinghu…...

安装更新upgrade导致ubuntu崩溃
安装更新导致ubuntu崩溃 前言uuid编不过,导致的崩溃 记录一些ubuntu崩溃的过程。 目前只有一个,以后遇到都放在这里,以提醒自己。 前言 如果从10000年看现在的linux,不是说不完美,而是糟透了。 linux的版本号…...

数学建模选MATLAB还是Python?
选择MATLAB还是Python进行数学建模,取决于多个因素,包括你的具体需求、个人偏好、项目要求以及你已有的技能。以下是一些考虑因素: 1. 易用性: • MATLAB:对于数学和工程问题,MATLAB提供了一个非常直观和…...

python数组增加元素
append、appext、insert,在某位置插入insert最在行。 (笔记模板由python脚本于2024年12月04日 19:41:46创建,本篇笔记适合python基础编程的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
