P3379 【模板】最近公共祖先(LCA)
【模板】最近公共祖先(LCA)
https://www.luogu.com.cn/problem/P3379
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式
第一行包含三个正整数 N , M , S N,M,S N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 N − 1 N-1 N−1 行每行包含两个正整数 x , y x, y x,y,表示 x x x 结点和 y y y 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 M M M 行每行包含两个正整数 a , b a, b a,b,表示询问 a a a 结点和 b b b 结点的最近公共祖先。
输出格式
输出包含 M M M 行,每行包含一个正整数,依次为每一个询问的结果。
样例 #1
样例输入 #1
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
样例输出 #1
4
4
1
4
4
提示
对于 30 % 30\% 30% 的数据, N ≤ 10 N\leq 10 N≤10, M ≤ 10 M\leq 10 M≤10。
对于 70 % 70\% 70% 的数据, N ≤ 10000 N\leq 10000 N≤10000, M ≤ 10000 M\leq 10000 M≤10000。
对于 100 % 100\% 100% 的数据, 1 ≤ N , M ≤ 500000 1 \leq N,M\leq 500000 1≤N,M≤500000, 1 ≤ x , y , a , b ≤ N 1 \leq x, y,a ,b \leq N 1≤x,y,a,b≤N,不保证 a ≠ b a \neq b a=b。
样例说明:
该树结构如下:

第一次询问: 2 , 4 2, 4 2,4 的最近公共祖先,故为 4 4 4。
第二次询问: 3 , 2 3, 2 3,2 的最近公共祖先,故为 4 4 4。
第三次询问: 3 , 5 3, 5 3,5 的最近公共祖先,故为 1 1 1。
第四次询问: 1 , 2 1, 2 1,2 的最近公共祖先,故为 4 4 4。
第五次询问: 4 , 5 4, 5 4,5 的最近公共祖先,故为 4 4 4。
故输出依次为 4 , 4 , 1 , 4 , 4 4, 4, 1, 4, 4 4,4,1,4,4。
2021/10/4 数据更新 @fstqwq:应要求加了两组数据卡掉了暴力跳。
代码
倍增算法
#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
vector<vector<int>> e; // 存储每个节点连接的边
vector<vector<int>> fa; // 存储节点的跳跃情况
vector<int> dep; // 存储节点的深度void dfs(int x, int y) {dep[x] = dep[y] + 1; // 深度加1fa[x][0] = y; // 确认父节点// 从前往后推出父节点for (int i = 1; i <= 18; i++) {fa[x][i] = fa[fa[x][i - 1]][i - 1];}// 递归遍历for (auto i : e[x]) {// 如果不是父节点,那么就dfsif (i != y) dfs(i, x);}
}int lca(int u, int v) {// 首先保证u深度更大if (dep[u] < dep[v]) swap(u, v);// 将u和v深度对齐for (int i = 18; ~i; i--) {// 一直往上跳,不断接近vif (dep[fa[u][i]] >= dep[v]) {u = fa[u][i];}}// 如果u和v相等,那么直接返回vif (u == v) return v;// 否则一起向上寻找lcafor (int i = 18; ~i; i--) {if (fa[u][i] != fa[v][i]) {u = fa[u][i];v = fa[v][i];}}// 因为一定会到lca的下一层,所以直接返回最后的父节点return fa[u][0];
}void solve() {// N为树的节点个数,M为询问个数,S为根节点序号int N, M, S;cin >> N >> M >> S;e.resize(N + 1);fa.resize(N + 1);for (int i = 0; i <= N; i++) {// N最大为500000,所以深度最高为2的18次方,19就会越界fa[i].resize(19);}dep.resize(N + 1, 0); // 初始化深度为0// 输入N-1个边for (int i = 1; i <= N - 1; i++) {int a, b;cin >> a >> b;// 最开始无向,所以两个都要插入e[a].push_back(b);e[b].push_back(a);}dfs(S, 0);// 输入M个查询for (int i = 1; i <= M; i++) {int u, v;cin >> u >> v;// 寻找lcacout << lca(u, v) << endl;}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);solve();return 0;
}
tarjan算法
#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
vector<bool> vis; // 用来存储是否已经访问
vector<vector<int>> e; // 存储每个节点连接的边
vector<int> fa; // 存储节点的父节点
vector<vector<pair<int, int>>> query; // 存储要查询的
vector<int> ans; // 存储结果
// 并查集——路径压缩
int find(int u) {if (u == fa[u]) return u;return fa[u] = find(fa[u]);
}void tarjan(int u) {// 首先标记已经访问vis[u] = true;// 访问该节点的所有子节点for (int v : e[u]) {// 不能访问已经访问过的节点if (!vis[v]) {// 递归tarjantarjan(v);// 明确父节点fa[v] = u;}}// 在离开时查询for (auto q : query[u]) {int v = q.first;int i = q.second;// 如果该节点的另一半也访问过了,那么说明现在可以找到共同祖先if (vis[v]) {ans[i] = find(v);}}
}void solve() {// N为树的节点个数,M为询问个数,S为根节点序号int N, M, S;cin >> N >> M >> S;fa.resize(N + 1);vis.resize(N + 1);e.resize(N + 1);query.resize(M + 1);ans.resize(M + 1);// 初始化每个节点的父节点为自己iota(fa.begin(), fa.end(), 0);// 输入N-1个边for (int i = 1; i <= N - 1; i++) {int a, b;cin >> a >> b;// 最开始无向,所以两个都要插入e[a].push_back(b);e[b].push_back(a);}// 输入M个查询for (int i = 1; i <= M; i++) {int u, v;cin >> u >> v;// tarjan为离线算法,所以要先存储查询query[u].push_back({ v, i });query[v].push_back({ u, i });}// tarjantarjan(S);// 输出存储的结果for (int i = 1; i <= M; i++) {cout << ans[i] << endl;}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);solve();return 0;
}
-
并查集的路径压缩:路径压缩的基本思想是,在执行查找操作时,将访问路径上的所有节点直接连接到根节点上。这样做的目的是在下一次查找操作时,能直接访问到根节点,从而减少路径长度,提高查找效率。
// 并查集——路径压缩 int find(int u) {if (u == fa[u]) return u;return fa[u] = find(fa[u]); }
相关文章:

P3379 【模板】最近公共祖先(LCA)
【模板】最近公共祖先(LCA) https://www.luogu.com.cn/problem/P3379 题目描述 如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。 输入格式 第一行包含三个正整数 N , M , S N,M,S N,M,S,分别表示…...

2030. gitLab A仓同步到B仓
文章目录 1 A 仓库备份 到 B 仓库2 B 仓库修改main分支的权限 1 A 仓库备份 到 B 仓库 #!/bin/bash# 定义变量 REPO_DIR"/home/xhome/opt/git_sync/zz_xx_xx" # 替换为你的本地库A的实际路径 REMOTE_ORIGIN"http://192.168.1.66:8181/zzkj_software/zz_xx_xx.…...
源代码并和eclipse做关联)
网易博客旧文-----如何在WINDOWS下载安卓(android)源代码并和eclipse做关联
如何在WINDOWS下载安卓(android)源代码并和eclipse做关联 2013-02-05 17:27:16| 分类: 安卓开发 | 标签: |举报 |字号大中小 订阅 编写安卓程序时,有时想看看安卓某些类的实现,但默认情况下环境是不带的。…...

MATLAB中axes函数用法
目录 语法 说明 示例 在图窗中定位多个坐标区 将坐标区设置为当前坐标区 在选项卡上创建坐标区 axes函数的功能是创建笛卡尔坐标区。 语法 axes axes(Name,Value) axes(parent,Name,Value) ax axes(___) axes(cax) 说明 axes 在当前图窗中创建默认的笛卡尔坐标区&…...
)
构建 Java Web 应用程序:实现简单的增删查改(Mysql)
简介 本教程将指导您如何使用Java Servlet和JSP技术构建一个简单的Web应用程序。该应用程序将包括用户注册、登录、注销(删除用户信息)、修改密码以及根据性别查询用户信息等功能。我们将使用MySQL数据库来存储用户数据。 环境准备 Java Development …...

3d行政区划-中国地图
前言 技术调研:做底代码平台的3d行政区组件 写的demo 效果图: 实现的功能项 地标、打点、飞线、three.js 3d 中国地图的一些基础配置补充 geo中国地图文件获取 其他项:包 "dependencies": {"d3": "^7.9.0","d3-…...

适合存储时序数据的数据库和存储系统
时序数据的存储通常要求高效地处理大量按时间排序的数据,同时支持快速查询、实时分析和高并发写入。以下是一些适合存储时序数据的数据库和存储系统: 1. InfluxDB 概述:InfluxDB 是一个开源的时序数据库,专门为处理时序数据而设…...
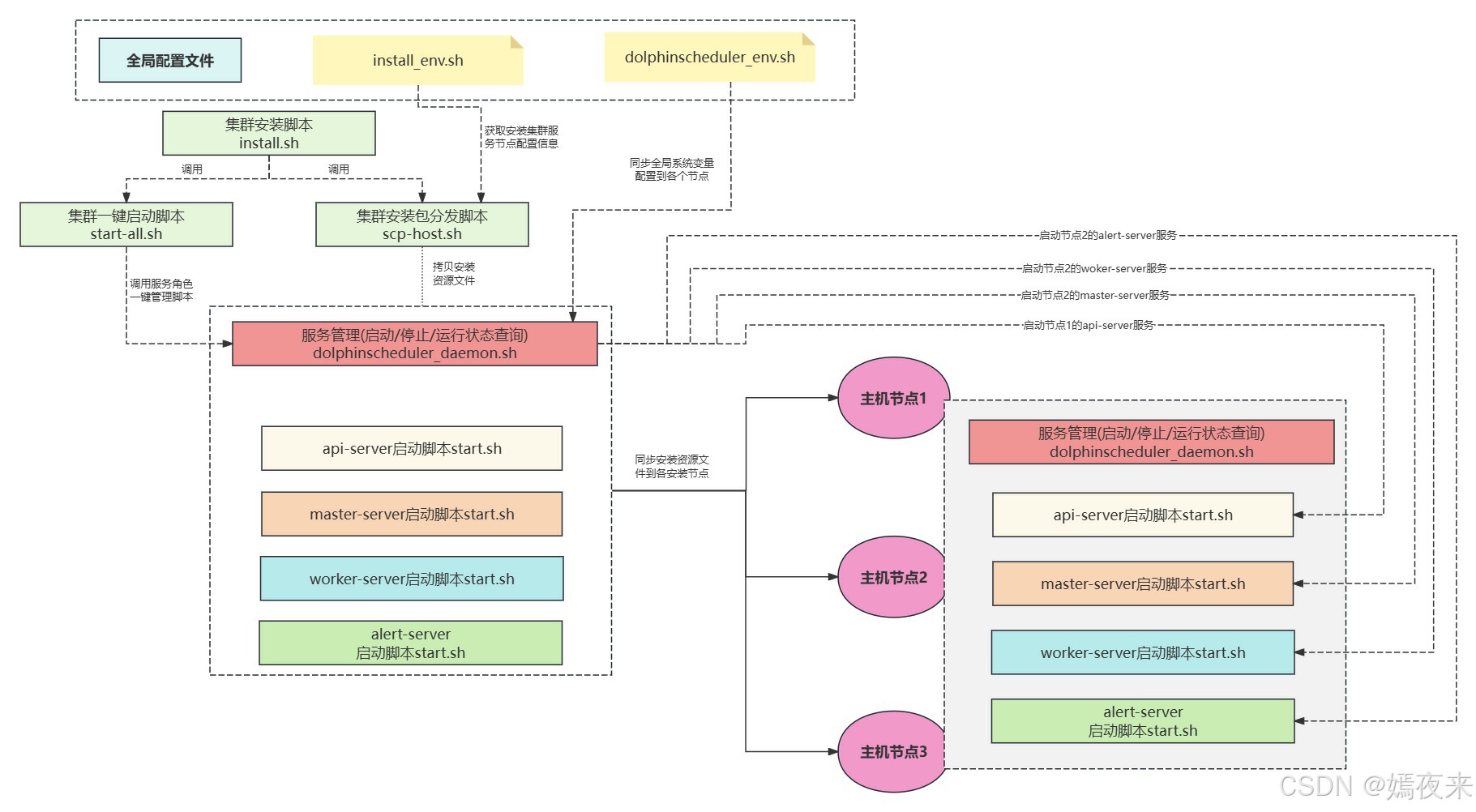
dolphinscheduler集群服务一键安装启动实现流程剖析
1.dolphinscheduler的安装部署 dolphinscheduler服务的安装部署都是非常简单的,因为就服务本身而言依赖的服务并不多。 mysql / postgresql。由于需要进行元数据及业务数据的持久化存储所以需要依赖于数据库服务,数据库服务支持mysql、postgresql等&am…...

深入了解Linux —— 学会使用vim编辑器
前言 学习了Linux中的基本指令也理解了权限这一概念,但是我们怎么在Linux下写代码呢? 本篇就来深入学习Linux下的vim编辑器;学会在Linux下写代码。 软件包管理器 1. 软件包? 在Linux下安装软件,通常是下载程序的源码…...

C05S01-Web基础和HTTP协议
一、Web基础 1. Web相关概念 1.1 URL URL(Uniform Resource Locator,统一资源定位符),是一种用于在互联网上标识和定位资源的标准化地址,提供了一种访问互联网上特定资源的方法。URL的基本格式如下所示:…...

MIT工具课第六课任务 Git基础练习题
如果您之前从来没有用过 Git,推荐您阅读 Pro Git 的前几章,或者完成像 Learn Git Branching 这样的教程。重点关注 Git 命令和数据模型相关内容; 相关内容整理链接:Linux Git新手入门 git常用命令 Git全面指南:基础概念…...

计算机网络安全
从广义来说,凡是涉及到网络上信息的机密性、报文完整性、端点鉴别等技术和理论都是网络安全的研究领域。 机密性指仅有发送方和接收方能理解传输报文的内容,而其他未授权用户不能解密(理解)该报文报文完整性指报文在传输过程中不…...

Delphi 实现键盘模拟、锁定键盘,锁定鼠标等操作
Delphi 模拟按键的方法 SendMessageA 说明: 调用一个窗口的窗口函数,将一条消息发给那个窗口。除非消息处理完毕,否则该函数不会返回SendMessage所包含4个参数: 1. hwnd 32位的窗口句柄窗口可以是任何类型的屏幕对象,因为Win32能够维护大多数…...

RTK数据的采集方法
采集RTK(实时动态定位)数据通常涉及使用高精度的GNSS(全球导航卫星系统)接收器,并通过基站和流动站的配合来实现。本文给出RTK数据采集的基本步骤 文章目录 准备设备设置基站设置流动站数据采集数据存储与处理应用数据…...

Next.js 入门学习
一、引言 在现代 Web 开发领域,Next.js 已成为构建高性能、可扩展且用户体验卓越的 React 应用程序的重要框架。它基于 React 并提供了一系列强大的特性和工具,能够帮助开发者更高效地构建服务器端渲染(SSR)、静态站点生成&#…...

2024年认证杯SPSSPRO杯数学建模B题(第一阶段)神经外科手术的定位与导航解题全过程文档及程序
2024年认证杯SPSSPRO杯数学建模 B题 神经外科手术的定位与导航 原题再现: 人的大脑结构非常复杂,内部交织密布着神经和血管,所以在大脑内做手术具有非常高的精细和复杂程度。例如神经外科的肿瘤切除手术或血肿清除手术,通常需要…...

安卓底层相机流的传输方式
这是安卓 相机流的定义 typedef enum {CAM_STREAMING_MODE_CONTINUOUS, /* continous streaming */CAM_STREAMING_MODE_BURST, /* burst streaming */CAM_STREAMING_MODE_BATCH, /* stream frames in batches */CAM_STREAMING_MODE_MAX} cam_streaming_mode_t; 在ca…...

【单链表】(更新中...)
一、 题单 206.反转链表203.移除链表元素 876.链表的中间结点BM8 链表中倒数最后k个结点21.合并两个有序链表 二、题目简介及思路 206.反转链表 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 思路简单,但是除了要两个指针进…...
开源堡垒机JumpServer配置教程:使用步骤与配置
开源堡垒机JumpServer配置教程:使用步骤与配置 上一篇文章星哥讲了如何安装JumpServer堡垒机,本篇文章来讲如何配置和使用JumpServer。 安装成功后,通过浏览器访问登录 JumpServer 地址: http://<JumpServer服务器IP地址>:<服务运…...

上门服务小程序开发,打造便捷生活新体验
随着互联网的快速发展,各种上门服务成为了市场的发展趋势,不管是各种外卖、家政、美甲、维修、按摩等等,都可以提供上门服务,人们足不出户就可以满足各种需求,商家也能够获得新的拓展业务渠道,提高整体收益…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
