2024年华中杯数学建模B题使用行车轨迹估计交通信号灯周期问题解题全过程文档及程序
2024年华中杯数学建模
B题 使用行车轨迹估计交通信号灯周期问题
原题再现
某电子地图服务商希望获取城市路网中所有交通信号灯的红绿周期,以便为司机提供更好的导航服务。由于许多信号灯未接入网络,无法直接从交通管理部门获取所有信号灯的数据,也不可能在所有路口安排人工读取信号灯周期信息。所以,该公司计划使用大量客户的行车轨迹数据估计交通信号灯的周期。请帮助该公司解决这一问题,完成以下任务。已知所有信号灯只有红、绿两种状态。
1. 若信号灯周期固定不变,且已知所有车辆的行车轨迹,建立模型,利用车辆行车轨迹数据估计信号灯的红绿周期。附件1中是5个不相关路口各自一个方向连续1小时内车辆的轨迹数据,尝试求出这些路口相应方向的信号灯周期,并按格式要求填入表1。
2. 实际上,只有部分用户使用该公司的产品,即只能获取部分样本车辆的行车轨迹。同时,受各种因素的影响,轨迹数据存在定位误差,误差大小未知。讨论样本车辆比例、车流量、定位误差等因素对上述模型估计精度的影响。附件2中是另外5个不相关路口各自一个方向连续1小时内样本车辆的轨迹数据,尝试求出这些路口相应方向的信号灯周期,按同样的格式要求填入表2。
3. 如果信号灯周期有可能发生变化,能否尽快检测出这种变化,以及变化后的新周期?附件3中是另外6个不相关路口各自一个方向连续2小时内样本车辆的轨迹数据,判断这些路口相应方向的信号灯周期在这段时间内是否有变化,尝试求出周期切换的时刻,以及新旧周期参数,按格式要求填入表3,并指明识别出周期变化所需的时间和条件。
4. 附件4是某路口连续2小时内所有方向样本车辆的轨迹数据,请尝试
识别出该路口信号灯的周期。
附件1:路口A1、A2、A3、A4、A5各自一个方向连续1小时内车辆轨迹数据
附件2:路口B1、B2、B3、B4、B5各自一个方向连续1小时内样本车辆轨迹数据
附件3:路口C1、C2、C3、C4、C5、C6各自一个方向连续2小时内样本车辆轨迹数据
附件4:路口D所有方向连续2小时内样本车辆轨迹数据
附件5:数据文件说明及结果表格
1、轨迹数据文件格式。适用于附件1-附件4所有轨迹数据文件。纯文本文件,第一行为标题行,各列以英文逗号分隔,共5列,分别为时间点、车辆ID、当前位置X坐标、当前位置Y坐标。时间点单位为秒,第0秒开始,每1秒采样一次。坐标单位为米。车辆ID仅用于区分同一个文件中的不同车辆。车辆ID不一定是连续编号。不同文件中,相同ID的车辆没有任何联系。同一车道可能只允许一个方向前进,也可能允许两个方向前进,如直行或左转、直行或右转等。
2、表1:路口A1-A5各自一个方向信号灯周期识别结果

3、表2:路口B1-B5各自一个方向信号灯周期识别结果

4、表3:路口C1-C6各自一个方向信号灯周期识别结果

说明:“周期切换时刻”是指信号灯周期发生变化的具体时间点,以第一个变化后的时长区间的起点计。如果信号灯周期没有变化,则“周期切换时刻”填写“无”。如果信号灯周期多次切换,按照上述格式,自行延长表格依次填写。
整体求解过程概述(摘要)
本文根据某电子地图服务商提供的行车轨迹数据,建立了基于两阶段STFT的时频分析模型和基于DBSCAN聚类分析改进的周期检测模型对不同路口的周期进行估计;然后利用贝叶斯变点检测求出周期变化时各阶段的周期参数。
问题一中,本文首先对 A1-A5 五个互不相关路口的行车轨迹数据进行离群点检测、轨迹连续性检验,然后进行异常值处理。然后,通过指标构建得到车辆运行加速度状态的时序数据,本文建立了基于两阶段STFT的时频分析模型,对时序数据进行周期特征挖掘,得出信号灯的周期性规律。然后通过绘制功率谱密度图得到信号灯完整周期长度,再将车辆处于停车状态最长的时间作为红灯周期,进而得到绿灯周期。最终得到 A1-A5 路口的红灯周期分别为[73,59,81,69,63];绿灯周期分别为[33,28,26,19,26]。
问题二中,由于样本车辆减少,存在定位偏差等情况,因此,本文在第一问所建立模型的基础上融入DBSCAN聚类分析,得到红绿灯完整周期时长或者完整周期时长的倍数,然后利用基于两阶段STFT的时频分析模型对红绿灯周期进行估计,得到B1-B5 路口的红灯周期分别为[78,83,54,78,95],绿灯周期分别为[27,33,34,27,21]。最后对模型设计对比实验分析探究影响因素,发现车流量减小对模型的影响较大,定位误差因素对模型基本无影响,发现模型有较高的鲁棒性。
问题三中,每个路口信号灯周期均可能发生变化,故本文使用贝叶斯变点检测对周期的变化点进行检验;然后将时序数据沿变化点进行分段,对分段后的每段时序数据使用加Manning窗的FFT算法求解周期,得到C1-C6路口的主要完整周期长度分别为[88,88,105,105,88,105],每个路口周期变化次数分别为[6,5,3,0,4,0]。
问题四中,附件4给出的是某路口D所有方向的车辆轨迹数据,本文首先建立多方向汽车轨迹分解模型对该路口的车辆行驶方向进行分解,得到沿一个方向的所有车辆轨迹;再使用前文模型求解各个方向的周期,最后使用滑动窗口稳态检测对周期进行检验,得到路口所以方向完整红绿灯周期时长均为142s,且对向车道信号灯周期时间相同,符合现实红绿灯规律。
模型假设:
1、假设每个路口在正常情况下,不会发生交通事故、堵车等意外情况,道路通行仅受红绿灯信号的影响;
2、针对附件提供的数据,假设这些数据是真实可靠的,并且车辆在行驶过程中均遵守交通规则,因此可以直接基于这些数据进行计算分析;
3、假设题目中给出的若干路口的红绿灯信号情况是相互独立的,即上一个路口的红绿灯状态不会对下一个路口的红绿灯信号产生任何影响。
问题分析:
针对问题一,首先需要对车辆行车轨迹数据进行清洗,剔除异常值。这可以通过确实轨迹正方向、离群点检验、轨迹连续性检验等方式来识别异常点,并用通过差值进行替换,确保数据的连贯性。接下来,构建一系列反映车辆运行状态的指标,包括车辆运行状态、车辆速度、车辆加速度等。这些指标能够共同形成车辆状态的时序数据。最后,利用基于两阶段STFT的时频分析模型,可以对这些时序数据进行周期特征挖掘,得出车辆行驶的周期性规律。
针对问题二,只有部分用户在使用该公司的产品,因此只能获取部分样本车辆的行车轨迹数据。而且,样本车辆比例的减少、车流量的减少以及存在定位误差等因素,都会对上述STFT预测模型的预测精度产生较大的影响。因此,本文在第一问的基础上结合DBSCAN聚类分析,通过聚类可以得到这一次红灯结束的时间到下一次红灯结束的时间,即为红绿灯完整周期时长或者周期时长的倍数,进而得到红绿灯完整周期得大致范围,从而对第一问中的两阶段STFT的时频分析模型进行修正。
针对问题三,贝叶斯变点检测是一种用于发现时序数据中周期性变化点的有效方法。它建立在概率模型的基础之上,利用贝叶斯推断来识别数据序列中的变化点。具体而言,贝叶斯变点检测假设数据序列可以由不同的概率模型描述,每个模型对应于序列的一个状态。通过计算不同模型的后验概率,可以确定序列中最可能出现变化点的位置。与其他变点检测方法相比,贝叶斯变点检测不仅能够检测出变化的时间点,还可以量化变化的概率,从而更好地反映变化的程度和确定性。 因此本文使用贝叶斯变点检测检测出周期变化点,然后将时序数据沿变化点进行分段,对每段时序数据使用加manning窗的FFT算法求解周期,通过上述方式得到周期的变化时间点,然后对时间点分割,对分割后的数据采用前文模型,得到具体周期时间。
针对问题四,问题四涉及某路口的全方位数据,我们可以将其拆分为前述问题的子问题。具体来说,先对该路口的车辆运行模式进行分解分析,然后应用前文提及的模型对各个方向进行周期性特征提取。接下来,可以利用改进的线性互相关算法对周期预估结果进行验证。通过这种方式,们可以将问题四转化为先前提出的问题类型,并继续采用前文介绍的分析方法进行求解。这样不仅避免重复阐述,也能充分利用前期的建模和分析思路。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
import numpy as np
filename = 'data/2/B5.csv'
df = pd.read_csv(filename)
#对df.x,df.y做散点图,并做离群点检测
plt.figure(figsize=(8, 6))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#设置字体大小
plt.rcParams['font.size'] = 14
plt.scatter(df['x'], df['y'], label='车辆轨迹数据')
plt.xlabel('x',fontsize = 16)
plt.ylabel('y',fontsize = 16)
plt.title('车辆轨迹散点图')
###只放一部分return outlier_indices outlier_indices = detect_outliers(df['x'], df['y'])
outliers = df.iloc[outlier_indices]
print(f"Outlier indices: {outlier_indices}")
print(f"Number of outliers: {len(outlier_indices)}")
print(outliers)
#在图中画出异常点
plt.figure(figsize=(8, 6))
plt.scatter(df['x'], df['y'], label='车辆轨迹数据')
plt.scatter(outliers['x'], outliers['y'], color='red', label='异常点')
plt.xlabel('x')
plt.ylabel('y')
plt.title('车辆轨迹散点图')
plt.legend()
plt.savefig('data2/img/B5_scatterDetect.png')
plt.show() from statsmodels.tsa.seasonal import seasonal_decompose
#
#读取data中1中的A1.csv文件
import pandas as pd
import math
import os
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd 2 df.loc[i[1].index,'x_y'] = df.loc[i[1].index,'x_y'].fillna(2)
#对df中x_y列中的值大于0.5的行,添加一个标签,值为1,否则为0,列名为label
)
ts = data['count']
#探究ts的周期性
decomposition = seasonal_decompose(ts,period=72, model="add")
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
plt.plot(ts, label='Original')
plt.legend(loc='best')
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.savefig('data2/img/D_trend.png',dpi=200)
plt.show() import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf plt.legend()
plt.show() # 自相关函数(ACF)分析
plt.figure(figsize=(12, 4))
plot_acf(diff_data, lags=1, title="差分序列自相关函数(ACF)")
plt.show() array = [ 134, 246, 398, 485, 685, 948, 1028, 1213, 1653, 1828, 2004, 2092, 2245, 2621, 2796, 2886, 3148, 3325, 3390, 3500, 3589, 3677, 3764, 3940, 4028, 4292, 4380, 4469, 4646, 4820, 4997, 5172, 5436, 5612, 5704, 5964, 6140, 6228, 6381, 6581, 6828, 7108, 7196] percentage_threshold = 8 # 百分比阈值
pe = 88
differences = []
previous_difference = array[1] - array[0]
change_points = [] for i in range(2, len(array)): current_difference = array[i] - array[i - 1] rsample_freq = fftfreq(fft_series.size) pos_mask = np.where(sample_freq > 0) freqs = sample_freq[pos_mask] powers = power[pos_mask] top_k_seasons = 3 top_k_idxs = np.argpartition(powers, -top_k_seasons)[-top_k_seasons:] top_k_power = powers[top_k_idxs] fft_periods = (1 / freqs[top_k_idxs]).astype(int) print(f"top_k_power: {top_k_power}") print(f"fft_periods: {fft_periods}") NFFT = 256 TEMP = np.abs(np.fft.fft(ts.values, n=NFFT)) PSD = (TEMP[0:NFFT//2+1])**2 / NFFT frequencies = np.linspace(0, 0.78/2, NFFT//2+1) # 单边频率轴,从0到采样率一半 periods = 1./frequencies # 将频率转换为周期 fig, ax = plt.subplots() ax.semilogy(periods, PSD, linewidth=1.5) # 使用对数尺度展示功率谱密度 #标出periods范围为50~100间的对应PSD的最大值点 max_index = np.argmax((periods >= 50) & (periods <= 100) & (PSD > 0)) # 需确保 PSD 大于
0,避免选取到噪声 ax.scatter(periods[max_index], PSD[max_index], color='red', marker='o', label=f"最大PSD点对
应周期为: {periods[max_index]:.2f}") # print(periods[np.argmax(PSD)], PSD[np.argmax(PSD)]) # ax.scatter(periods[np.argmax(PSD)], PSD[np.argmax(PSD)], color='red', s=100) ax.set_xlabel('周期(秒)') ax.set_ylabel('PSD值') ax.grid(True) ax.legend() plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False plt.savefig('data2/img/STFT.png',dpi=200) plt.show() from statsmodels.tsa.stattools import acf for lag in fft_periods: acf_score = acf(ts.values, nlags=lag)[-1] print(f"lag: {lag} fft acf: {acf_score}") expected_lags = np.array([30, 60, 90]).astype(int) for lag in expected_lags: acf_score = acf(ts.values, nlags=lag, fft=False)[-1] print(f"lag: {lag} expected acf: {acf_score}") pl = df print(pl.groupby('vehicle_id')['state'].sum().max(),pl.groupby('vehicle_id')['state'].sum().idxmax()) print(pl.groupby('vehicle_id')['state'].sum().nlargest(2).iloc[1],pl.groupby('vehicle_id')['state'].sum().nlargest(2).index[1]) print(pl.groupby('vehicle_id')['state'].sum().nlargest(3).mean()) sns.distplot(pl.groupby('vehicle_id')['state'].sum(),bins=20)
STFT('data/4/D.csv')
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2024年华中杯数学建模B题使用行车轨迹估计交通信号灯周期问题解题全过程文档及程序
2024年华中杯数学建模 B题 使用行车轨迹估计交通信号灯周期问题 原题再现 某电子地图服务商希望获取城市路网中所有交通信号灯的红绿周期,以便为司机提供更好的导航服务。由于许多信号灯未接入网络,无法直接从交通管理部门获取所有信号灯的数据&#x…...

高效查找秘密武器一:位图
有这样的一个问题: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数 中。 那么我们一般会想到这样做的 1.遍历,时间复杂度O(n) 2.排序(N*logN),…...

自回归模型(AR )
最近看到一些模型使用了自回归方法,这里就学习一下整理一下相关内容方便以后查阅。 自回归模型(AR ) 自回归模型(AR )AR 模型的引入AR 模型的定义参数的估计方法模型阶数选择平稳性与因果性条件自相关与偏自相关函数优…...

Linux内核 -- Linux驱动从设备树dts文件中读取字符串信息的方法
从Linux设备树读取字符串信息 在Linux内核中,从设备树(DTS)中读取字符串信息,通常使用内核提供的设备树解析API。这些API主要位于<linux/of.h>头文件中。 常用函数解析 1. of_get_property 获取设备树中的属性。原型:con…...

图片懒加载+IntersectionObserver
通过IntersectionObserver实现图片懒加载 在JavaScript中,图片懒加载可以通过监听滚动事件和计算图片距离视口顶部的距离来实现 在HTML中,将src属性设置为一个透明的1x1像素图片作为占位符,并将实际的图片URL设置为data-src属性。 <img c…...

MySQL的获取、安装、配置及使用教程
一、获取MySQL 官网地址:https://www.mysql.com MySQL产品:企业版(Enterprise)和社区版(Community)社区版是通过GPL协议授权的开源软件,可以免费使用。企业版是需要收费的商业软件 MySQL版本历史:5.0、5.5、5.6、5.7和8.0(最新版本)两种打包版本:MSI(安装版)和ZI…...

Odoo在线python代码开发
《Odoo在线python代码开发从入门到精通》 从简入手,由浅入深,Odoo开发不求人 以实例促理解,举一反三 从Python到Odoo,低代码开发的正解之路 代码视频讲解与代码注释配合,帮助用户真正理解每一句代码的作用 《Odoo在…...

在.NET 6中使用Serilog收集日志
此示例的完整详细信息:https://download.csdn.net/download/hefeng_aspnet/89998498 Serilog 是一个日志库,它提供对文件、控制台和其他几个地方的记录。它易于配置,并且具有干净且易于使用的界面。 Serilog具有无与伦比的输出目的地选择&…...

【D3.js in Action 3 精译_043】5.1 饼图和环形图的创建(中):D3 饼图布局生成器的配置方法
当前内容所在位置: 第五章 饼图布局与堆叠布局 ✔️ 5.1 饼图和环形图的创建 ✔️ 5.1.1 准备阶段(上篇)5.1.2 饼图布局生成器(中篇) ✔️5.1.3 圆弧的绘制5.1.4 数据标签的添加 文章目录 5.1.2 饼图布局生成器 The …...
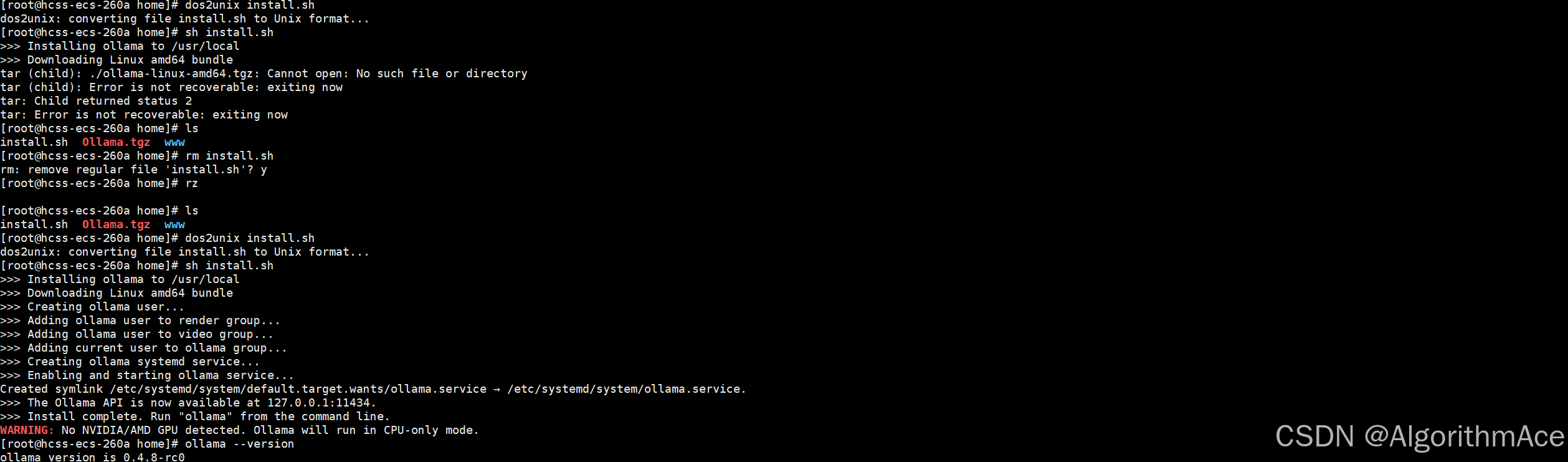
离线安装ollama到服务器
搜了很多教程不满意,弄了半天才弄好,这里记录下,方便以后的人用,那个在线下载太慢,怕不是得下载到明年。 一.从官网下在liunx版的tgz安装包 Releases ollama/ollama (github.com) 查看自己的服务器信息(参考 https:/…...

自动化点亮LED灯之程序编写
程序编写: #!/bin/shecho none > /sys/class/leds/led1/triggerecho none > /sys/class/leds/led2/triggerecho none > /sys/class/leds/led3/triggerecho 0 > /sys/class/leds/led1/brightnessecho 0 > /sys/class/leds/led2/brightnessecho 0 >…...

linux 系列服务器 高并发下ulimit优化文档
系统输入 ulimit -a 结果如下 解除或提高 Linux 系统的最大进程数 在高并发场景中,合理设置 Linux 系统的最大进程数对于提升服务器性能至关重要。以下是具体步骤: 临时修改 ulimit 设置 可以通过 ulimit 命令临时调整当前会话的最大进程数。 查看当前…...

人工智能入门数学基础:统计推断详解
人工智能入门数学基础:统计推断详解 目录 前言 1. 统计推断的基本概念 1.1 参数估计 1.2 假设检验 2. 统计推断的应用示例 2.1 参数估计示例:样本均值和置信区间 2.2 假设检验示例:t检验 3. 统计推断在人工智能中的应用场景 总结 前言…...

Spark区分应用程序 Application、作业Job、阶段Stage、任务Task
目录 一、Spark核心概念 1、应用程序Application 2、作业Job 3、阶段Stage 4、任务Task 二、示例 一、Spark核心概念 在Apache Spark中,有几个核心概念用于描述应用程序的执行流程和组件,包括应用程序 Application、作业Job、阶段Stage、任务Task…...

【Liunx篇】基础开发工具 - yum
文章目录 🌵一.Liunx下安装软件的方案🐾1.源代码安装🐾2.rpm包安装🐾3.包管理器进行安装 🌵二.软件包管理器-yum🌵三.yum的具体操作🐾1.查看软件包🐾2.安装软件包🐾3.卸载…...

docker学习笔记(五)--docker-compose
文章目录 常用命令docker-compose是什么yml配置指令详解versionservicesimagebuildcommandportsvolumesdepends_on docker-compose.yml文件编写 常用命令 命令说明docker-compose up启动所有docker-compose服务,通常加上-d选项,让其运行在后台docker-co…...
电子商务人工智能指南 4/6 - 内容理解
介绍 81% 的零售业高管表示, AI 至少在其组织中发挥了中等至完全的作用。然而,78% 的受访零售业高管表示,很难跟上不断发展的 AI 格局。 近年来,电子商务团队加快了适应新客户偏好和创造卓越数字购物体验的需求。采用 AI 不再是一…...

Hadoop3集群实战:从零开始的搭建之旅
目录 一、概念 1.1 Hadoop是什么 1.2 历史 1.3 三大发行版本(了解) 1.4 优势 1.5 组成💗 1.6 HDFS架构 1.7 YARN架构 1.8 MapReduce概述 1.9 HDFS\YARN\MapReduce关系 二、环境准备 2.1 准备模版虚拟机 2.2 安装必要软件 2.3 安…...

Kotlin设计模式之桥接模式
桥接模式用于将抽象部分与实现部分分离,使它们可以独立变化。Kotlin中可以通过接口和抽象类来实现桥接模式。以下是桥接模式的实现方法: 一. 基本桥接模式 在这种模式中,定义一个抽象部分和一个实现部分,通过组合将它们连接起来…...

详解组合模式
引言 有一种情况,当一组对象具有“整体—部分”关系时,如果我们处理其中一个对象或对象组合(区别对待),就可能会出现牵一发而动全身的情况,造成代码复杂。这个时候,组合模式就是一种可以用一致的…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
