数组 - 八皇后 - 困难

*************

C++

topic: 面试题 08.12. 八皇后 - 力扣（LeetCode）

*************

Good morning, gays, Fridary angin and try the hard to celebrate.

Inspect the topic:

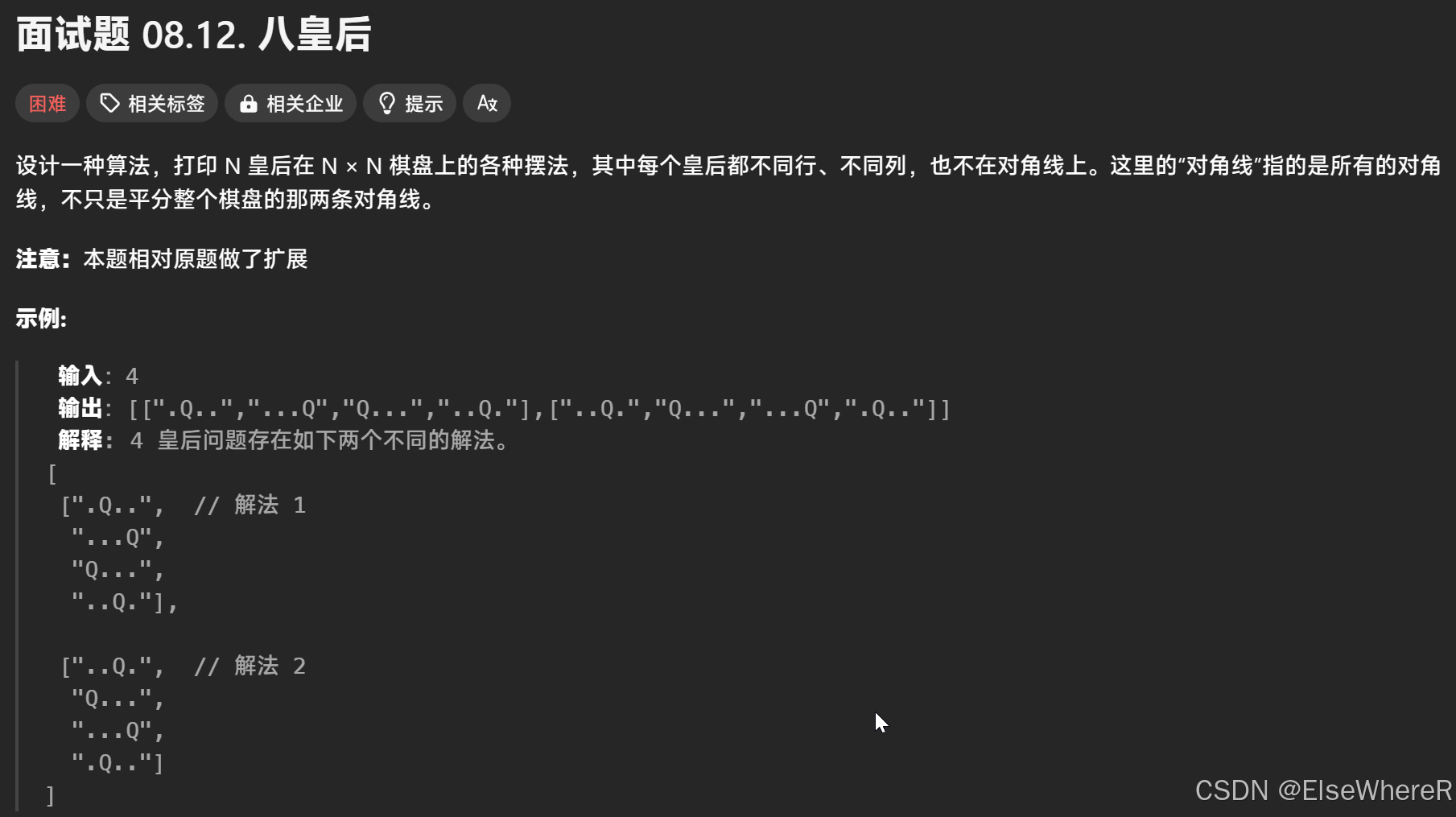
This topic I can understand it in a second.  And I do rethink a movie, which talks anout chess

This title imposes the same rectructions on queens as the rules for queens in chess. In chess, queens may move either stright and diagonally. And may by this code was applied in some chees games.

 

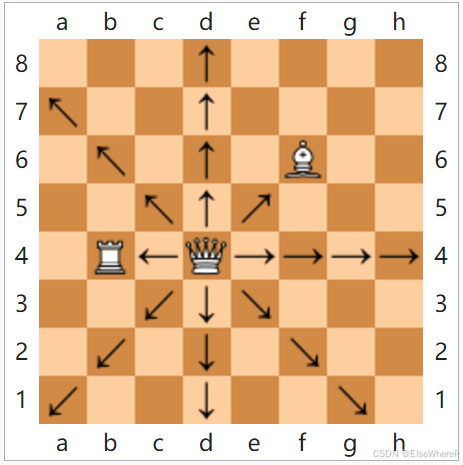
Back to the topic, try to find the topics I've done which is similar to t his topic. It seems like no one like this. 

Use matrix, I learned matrix from a teacher, Master Tang:

Greedy algorithm, I did yesterday, may work. Every step goes to the best way, and might have the happy ending in the end.

First, put the queen in matrix[1][1], then put the second  row, maxtrix[2][1] is forbidden cuz it is in the first column. Matrix[2][2] is forbidden cuz it in the diagonal. Put it in matrix[2][3]. Actally, make sure that  matrix[i][i] put nothing. 

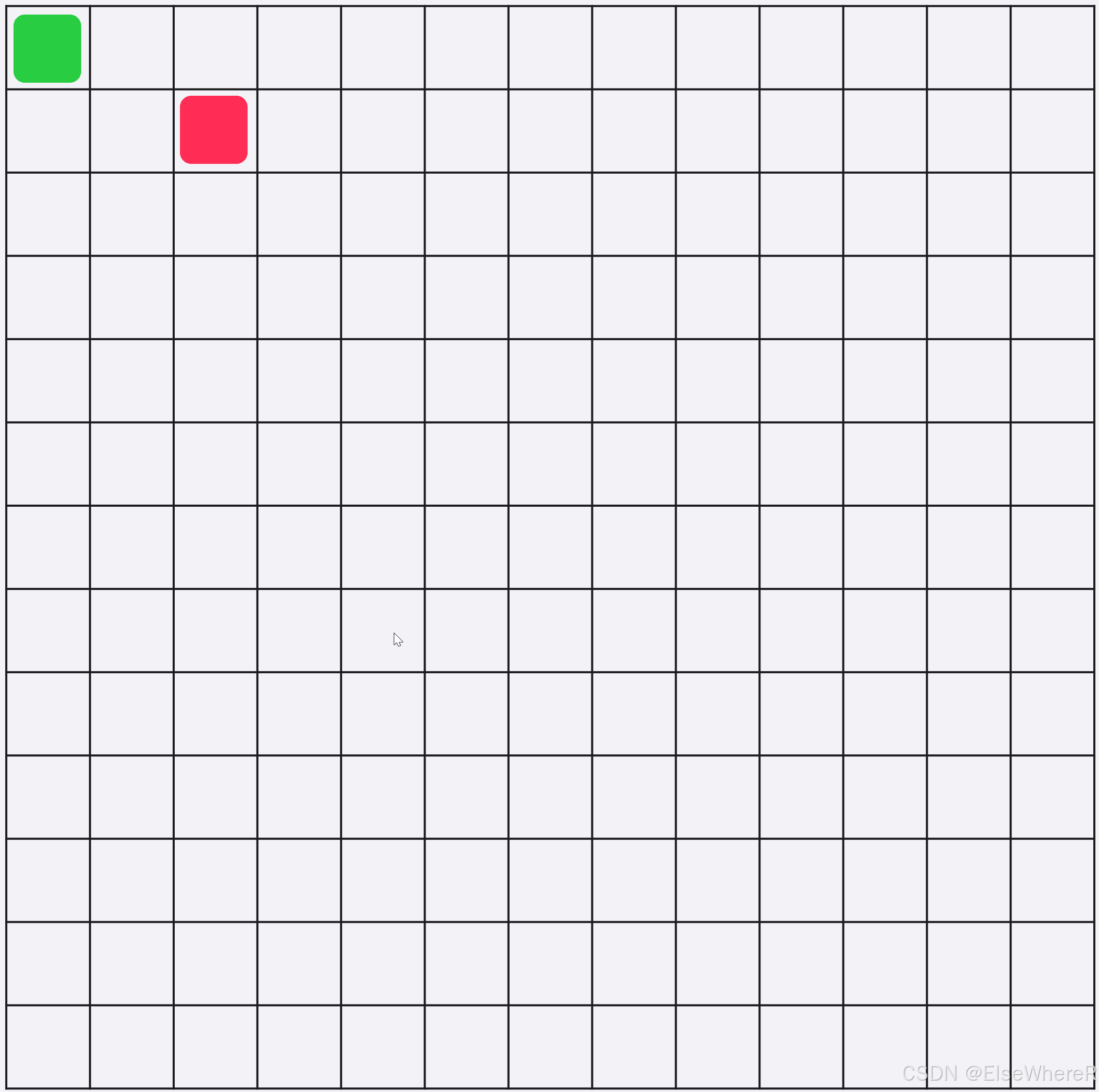
From the first row,  put the queen in the first column.

To the second row, put the queen in the first column, check if it conflicts with previous queens. If not, add a row. If so, change a column.

Take an example, N = 13, The position-array has 13 elements, each ranges from 0 to 12. 

For each increatment, generate a new array of positions. Check if the condition is satisfied for each array of positions. If satisfied, save it.                                                                         

When the last queen find her place, the war end.

This is a really new algorithm called Backtracking Algorithm.A backtracking algorithm is an algorithm that tries different things until it finds the right answer. It avoids doing unnecessary work. Backtracking algorithms are used to solve many kinds of problems. The usage of backtracking algorithm follows:

void backtrack(路径参数, 选择列表参数) {// 检查是否满足结束条件if (满足结束条件) {// 处理解决方案return;}// 遍历选择列表for (auto i : 选择列表) {// 添加当前选项到路径路径.push_back(i);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

Try to write the code:

need to find a right way to describe the chess board. matrix N × N doesnot work, the reason of it is that memory is everything for the computer, N × N use tooooooooooooo much storage. Never think about it. 

Every queen has different row, so it can be used in one-line matrix, for instace:

 it can be described as 4 multiply 4 

1. 1 0 0 0
2. 0 0 1 0
3. 0 1 0 0 
4. 0 0 0 1

also, a smarter way to describe is as follow:

array X = [1, 3, 2, 4], which means

1. the 1st  queen laies at row 1 column 1,
2. the 2nd queen laies at row 2 column 3,
3. the 3rd queen laies at row 3 column  2,
4. the 4th queen laies at row 4 column  4,

but how to tell the computer that the queens cannot stay in the diagonal? 

the same color's position is illegal. It can EZ tell that two queens on the same diagonal if and only if their row and column differences are equal. 
|row1 - row4| == |column4 - column1|

There's no need to double-check each row and column; only the diagonals. To check more efficiently, record which columns and diagonals have been used when placing the queens.

record this in three sets:

1. Columns where queens have already been placed.
2. Primary diagonal: row-column values on the same primary diagonal.
3. Sub-diagonal: row + column values where identical values are on the same sub-diagonal.

 so make up the code to describe the 3 sets in backtrack structure:

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (满足结束条件) {// 处理解决方案return;}// 遍历选择列表for (auto i : 选择列表) {// 添加当前选项到路径路径.push_back(i);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

move next, what is 满足结束条件? it is the row == n, the last queen finds her palace.

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 处理解决方案return;}// 遍历选择列表for (auto i : 选择列表) {// 添加当前选项到路径路径.push_back(i);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

and what is 处理解决方案？ That is return the result. But pay vital attention to the result like this:

make sure that the code return a string:

 

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 遍历选择列表for (auto i : 选择列表) {// 添加当前选项到路径路径.push_back(i);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

the next step is 遍历选择列表. This is the most diffcult step, including how to lay the queens. Make sure that every column has been visited.

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 遍历选择列表for (int col = 0; col < n; col++) {// 添加当前选项到路径路径.push_back(i);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

If there's already a queen in the column, main diagonal, or sub-diagonal where you're placing the queen, skip that spot.

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 遍历选择列表for (int col = 0; col < n; col++) {if ((cols_mask & (1ULL << col)) ||(diag1_mask & (1ULL << d1)) ||(diag2_mask & (1ULL << d2))) {continue; // 如果不安全，跳过这一列}// 添加当前选项到路径路径.push_back(i);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

in this special code :

if ((cols_mask & (1ULL << col)) ||(diag1_mask & (1ULL << d1)) ||(diag2_mask & (1ULL << d2))) {continue; // 如果不安全，跳过这一列}

1ULL meas 1 unsigned long long,  << means move 1 step to the left.

diag_mask is an integer, for example:

if col == 2, in binary system is 10;  1ULL << 2 is 4, in binary system is 100

see, in binary system, int 1 moves one step left.

then put the queen

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 遍历选择列表for (int col = 0; col < n; col++) {if ((cols_mask & (1ULL << col)) ||(diag1_mask & (1ULL << d1)) ||(diag2_mask & (1ULL << d2))) {continue; // 如果不安全，跳过这一列}// 在当前位置放置皇后queens.push_back(col);// 进行递归backtrack(路径, 更新的选择列表);// 回溯，移除当前选项路径.pop_back();}
}

and move to the next row:

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 遍历选择列表for (int col = 0; col < n; col++) {if ((cols_mask & (1ULL << col)) ||(diag1_mask & (1ULL << d1)) ||(diag2_mask & (1ULL << d2))) {continue; // 如果不安全，跳过这一列}// 在当前位置放置皇后queens.push_back(col);// 递归到下一行backtrack_bit(n, row + 1, cols_mask | (1ULL << col),diag1_mask | (1ULL << d1), diag2_mask | (1ULL << d2),queens, result);// 回溯，移除当前选项路径.pop_back();}
}

and next

void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) 
{// 检查是否满足结束条件if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 遍历选择列表for (int col = 0; col < n; col++) {if ((cols_mask & (1ULL << col)) ||(diag1_mask & (1ULL << d1)) ||(diag2_mask & (1ULL << d2))) {continue; // 如果不安全，跳过这一列}// 在当前位置放置皇后queens.push_back(col);// 递归到下一行backtrack_bit(n, row + 1, cols_mask | (1ULL << col),diag1_mask | (1ULL << d1), diag2_mask | (1ULL << d2),queens, result);// 回溯，移除当前皇后queens.pop_back();}
}

dont forget to initialize at the very beginning:

class Solution {
public:// 主函数，接收一个整数n，表示棋盘的大小vector<vector<string>> solveNQueens(int n) {vector<vector<string>> result; // 用于存储所有可能的解vector<int> queens; // 用于存储当前放置皇后的列位置// 从第0行开始回溯backtrack_bit(n, 0, 0, 0, 0, queens, result);return result; // 返回所有可能的解}private:// 回溯函数，参数包括棋盘大小n，当前行row，以及三个掩码void backtrack_bit(int n, int row, unsigned long long cols_mask,unsigned long long diag1_mask, unsigned long long diag2_mask,vector<int>& queens, vector<vector<string>>& result) {// 如果到达最后一行，说明找到了一个解if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 尝试在当前行的每一列放置皇后for (int col = 0; col < n; col++) {int d1 = row - col + (n - 1); // 对角线1的索引int d2 = row + col; // 对角线2的索引// 检查当前位置是否安全if ((cols_mask & (1ULL << col)) ||(diag1_mask & (1ULL << d1)) ||(diag2_mask & (1ULL << d2))) {continue; // 如果不安全，跳过这一列}// 在当前位置放置皇后queens.push_back(col);// 递归到下一行backtrack_bit(n, row + 1, cols_mask | (1ULL << col),diag1_mask | (1ULL << d1), diag2_mask | (1ULL << d2),queens, result);// 回溯，移除当前皇后queens.pop_back();}}
};

and of course it works:

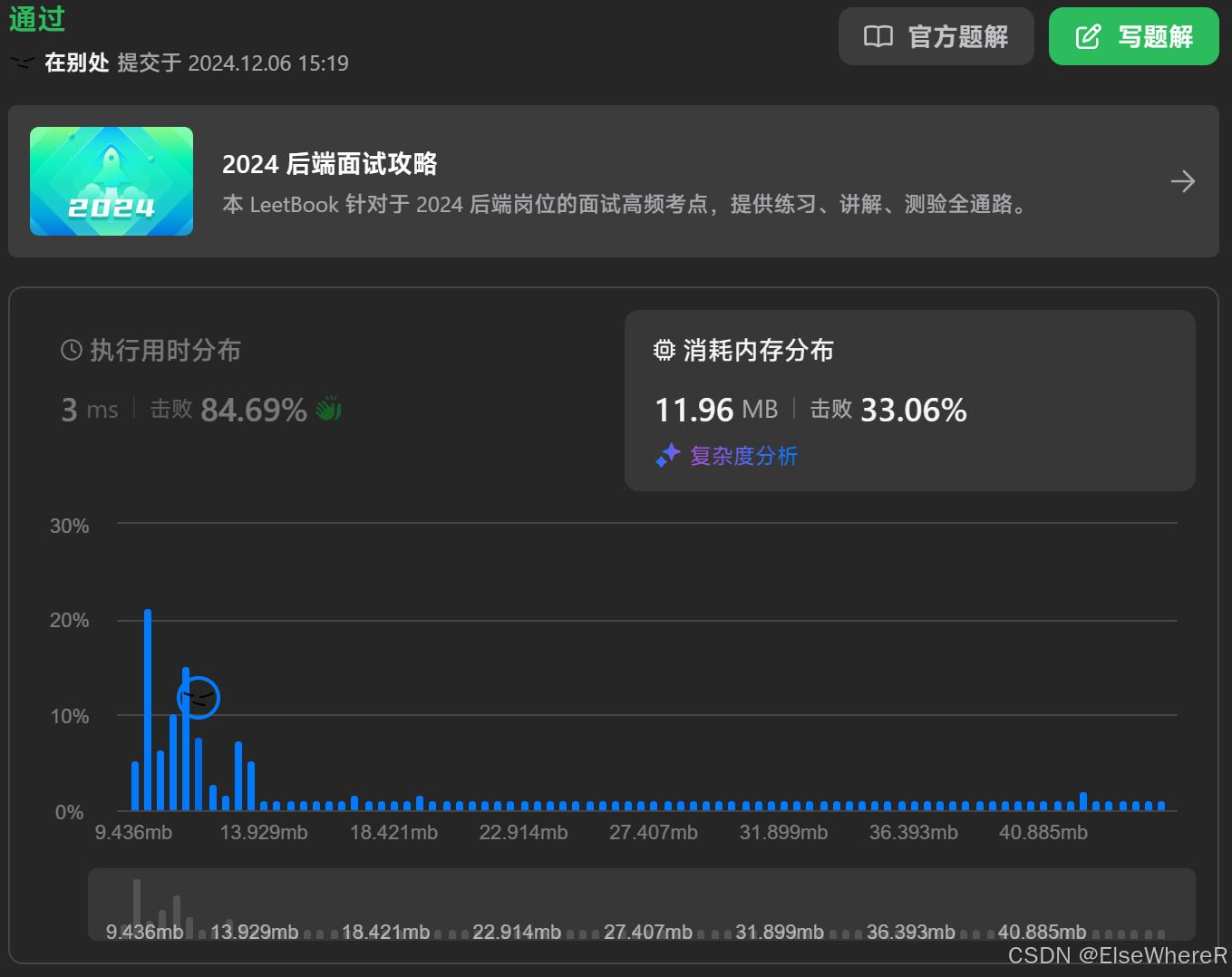
unsigned longlong can be replaced as unsigned long, to save the storge.

class Solution {
public:// 主函数，接收一个整数n，表示棋盘的大小vector<vector<string>> solveNQueens(int n) {vector<vector<string>> result; // 用于存储所有可能的解vector<int> queens; // 用于存储当前放置皇后的列位置// 从第0行开始回溯backtrack_bit(n, 0, 0, 0, 0, queens, result);return result; // 返回所有可能的解}private:// 回溯函数，参数包括棋盘大小n，当前行row，以及三个掩码void backtrack_bit(int n, int row, unsigned long cols_mask,unsigned long diag1_mask, unsigned long diag2_mask,vector<int>& queens, vector<vector<string>>& result) {// 如果到达最后一行，说明找到了一个解if (row == n) {// 生成棋盘的字符串表示vector<string> board;for (int i = 0; i < n; i++) {string row_str(n, '.'); // 初始化一行，全部为'.'row_str[queens[i]] = 'Q'; // 在皇后的位置放置'Q'board.push_back(row_str); // 将这一行添加到棋盘表示中}result.push_back(board); // 将整个棋盘添加到结果中return;}// 尝试在当前行的每一列放置皇后for (int col = 0; col < n; col++) {int d1 = row - col + (n - 1); // 对角线1的索引int d2 = row + col; // 对角线2的索引// 检查当前位置是否安全if ((cols_mask & (1UL << col)) ||(diag1_mask & (1UL << d1)) ||(diag2_mask & (1UL << d2))) {continue; // 如果不安全，跳过这一列}// 在当前位置放置皇后queens.push_back(col);// 递归到下一行backtrack_bit(n, row + 1, cols_mask | (1UL << col),diag1_mask | (1UL << d1), diag2_mask | (1UL << d2),queens, result);// 回溯，移除当前皇后queens.pop_back();}}
};

 and here is the magic:

 consume memory ranges from 11.96 to 12.15. 

reverse upgrading, sad.

anyway 

wish me have a good weekend.