Linx下自动化之路:Redis安装包一键安装脚本实现无网极速部署并注册成服务
目录
简介
安装包下载
安装脚本
服务常用命令
简介
通过一键安装脚本实现 Redis 安装包的无网极速部署,并将其成功注册为系统服务,开机自启。
安装包下载
redis-7.0.8.tar.gz![]() http://download.redis.io/releases/redis-7.0.8.tar.gz
http://download.redis.io/releases/redis-7.0.8.tar.gz
安装脚本
- 修改INSTALL_DIR:真实安装路径
- 修改PASSWORD:密码
- 将脚本(redis-install.sh)和安装包(redis-7.0.8.tar.gz)放置$INSTALL_DIR目录下
- 运行脚本sh redis-install.sh
#!/bin/bashINSTALL_DIR=/data
REDIS_VERSION=7.0.8
PASSWORD=123456# 检查是否已安装Redis
if command -v redis-server &>/dev/null; thenecho "已安装Redis"exit 0
fiecho "开始解压==================================================="
# 解压redis文件
tar zxvf redis-$REDIS_VERSION.tar.gz
echo "解压成功==================================================="echo "编译、安装开始==============================================="
# 编译、安装
cd $INSTALL_DIR/redis-$REDIS_VERSION && make && make PREFIX=$INSTALL_DIR/redis-$REDIS_VERSION install
echo "编译、安装成功==============================================="# 复制配置文件
cp $INSTALL_DIR/redis-$REDIS_VERSION/redis.conf /$INSTALL_DIR/redis-$REDIS_VERSION/bin# 创建启动脚本
cat << EOF> /etc/systemd/system/redis.service
[Unit]
Description=Redis
After=network.target[Service]
Type=forking
ExecStart=/$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis-server /$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis.conf
ExecReload=/$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis-server -s reload
ExecStop=/$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis-server -s stop
PrivateTmp=true[Install]
WantedBy=multi-user.target
EOF# 修改配置文件
sed -i 's/protected-mode yes/protected-mode no/' "$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis.conf"
sed -i 's/bind 127.0.0.1 -::1/# bind 127.0.0.1 -::1/' "$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis.conf"
echo "开启远程访问"sed -i 's/daemonize no/daemonize yes/' "$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis.conf"
echo "设置后台启动"sed -i 's/# requirepass foobared/requirepass $PASSWORD/' "$INSTALL_DIR/redis-$REDIS_VERSION/bin/redis.conf"
echo "设置密码"# 赋予权限
chmod +x /etc/init.d/redisecho "设置开机自启动"
# 设置开机自启动
chkconfig redis on# 启动
service redis start
echo "启动成功"
服务常用命令
# 启动服务
service redis start# 停止服务
service redis stop# 显示状态
service redis status
相关文章:
Linx下自动化之路:Redis安装包一键安装脚本实现无网极速部署并注册成服务
目录 简介 安装包下载 安装脚本 服务常用命令 简介 通过一键安装脚本实现 Redis 安装包的无网极速部署,并将其成功注册为系统服务,开机自启。 安装包下载 redis-7.0.8.tar.gzhttp://download.redis.io/releases/redis-7.0.8.tar.gz 安装脚本 修…...

VMware虚拟机搭建和镜像配置
VMware虚拟机搭建和镜像配置 下载安装VMware 开始下载 更改安装路径,需要一个大空间的盘 更改后下一步 下一步后,选择不主动升级更新 一直下一步 直到安装完毕 输入许可密钥,我下载的版本是12,输入完成点击输入ÿ…...

红日靶场vulnstark 4靶机的测试报告[细节](一)
目录 一、测试环境 1、系统环境 2、注意事项 3、使用工具/软件 二、测试目的 三、操作过程 1、信息搜集 2、漏洞利用Getshell ①Struts 2 s2-045漏洞 手工利用s2-45漏洞 Msf综合利用 ②Tomcat框架(CVE-2017-12615) ③phpMyAdmin(CVE-2018-12613) 构造语句写入冰蝎木…...

深入详解人工智能机器学习常见算法——线性回归算法
深入解析线性回归算法 线性回归是机器学习和统计学中最基本、最常用的预测建模技术之一。它通过线性关系描述因变量与一个或多个自变量之间的联系,帮助我们进行数据建模和预测。本篇文章将详细介绍线性回归的基础知识、算法原理、核心概念、实现方法以及其在实际问题…...

Python 开发环境搭建
Python 开发环境搭建 flyfish 版本 Ubuntu 22.04.5 LTS PyTorch 2.5.1 cuda 12.4 python 3.12.7安装 Anaconda3 依赖 sudo apt-get install libgl1-mesa-glx libegl1-mesa libxrandr2 libxrandr2 libxss1 libxcursor1 libxcomposite1 libasound2 libxi6 libxtst6安装命令 …...
相机标定函数calibrateCameraRO()的使用)
OpenCV相机标定与3D重建(9)相机标定函数calibrateCameraRO()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 cv::calibrateCameraRO 是 OpenCV 中用于相机标定的函数,它允许固定某些点来进行更精确的标定。 函数原型 double cv::calibrateCa…...

flink终止提交给yarn的任务
接上文:一文说清flink从编码到部署上线 1.查看正在执行的flink 访问地址(参考):http://10.86.97.191:8099/cluster/apps 2.终止任务 yarn application -kill appID 本文为: yarn application -kill application_17…...

算法刷题Day14:BM36 判断是不是平衡二叉树
题目链接 描述 输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。 在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树 平衡二叉树(Balanced Binary Tree),具有以下性质:它是…...

【Golang】Go语言编程思想(六):Channel,第一节,介绍Channel
Channel 下面的几个例子将会展示如何定义一个 channel: func chanDemo() {var c chan int // chan int 的含义是, c 是一个 channel, 里面的内容是 int// 上面的声明语句将会创建一个 nil channel, c nil, 它的作用将在 select 当// 中体现 }创建一个非 nil 的 c…...

【Flux.jl】 卷积神经网络
Flux.jl 是包含卷积神经网络的, 但是官方API文件中没有给出一个完整的程序框架, 只是对所需神经元给了局部解释, 此外对 model-zoo 模型动物园中的案例没有及时跟着 Flux.jl 的版本更新, 也无法运行出来结果。 因此本文搭建了一个完整可训练的卷积神经网络。 Conv 卷积算子…...

大模型在辅导场景的深度应用,猿辅导素养课推出启发性“AI作文通”
猿辅导集团旗下的飞象星球面向学校发布“飞象AI作文”,让教育大模型成为老师的AI批改助手、学生的写作助手。芥末堆注意到,猿辅导集团旗下的猿辅导素养课也推出了名为“AI作文通”的AI作文功能,已于7月正式大规模上线,在AI教育领域…...

深入了解架构中常见的4种缓存模式及其实现
4种缓存模式 随着应用程序的复杂性日益增加,缓存管理变得至关重要。缓存不仅能有效减轻数据库负载,还能显著提升数据访问速度。选择合适的缓存模式能够在不同的业务场景下发挥出最佳效果。 本文将详细介绍四种常见的缓存模式:Cache-Aside (…...

Hermes engine on React Native 0.72.5,function无法toString转成字符串
问题描述 Hermes engine on React Native 0.72.5,function无法toString转成字符串 环境 npm6.14.18 node16.17.1项目依赖 "react": "18.2.0", "react-dom": "18.2.0", "react-native": "0.72.5", …...

Spring Boot + MySQL 多线程查询与联表查询性能对比分析
Spring Boot MySQL: 多线程查询与联表查询性能对比分析 背景 在现代 Web 应用开发中,数据库性能是影响系统响应时间和用户体验的关键因素之一。随着业务需求的不断增长,单表查询和联表查询的效率问题日益凸显。特别是在 Spring Boot 项目中࿰…...

Java 设计模式~工厂模式
在java开发,工厂模式应用场景有哪些?在Spring boot原码中 有哪些工厂类,并做相应的代码介绍。 工厂模式 工厂模式(Factory Pattern)是Java中一种常用的创建型设计模式,它提供了一种创建对象的最佳方式。此…...
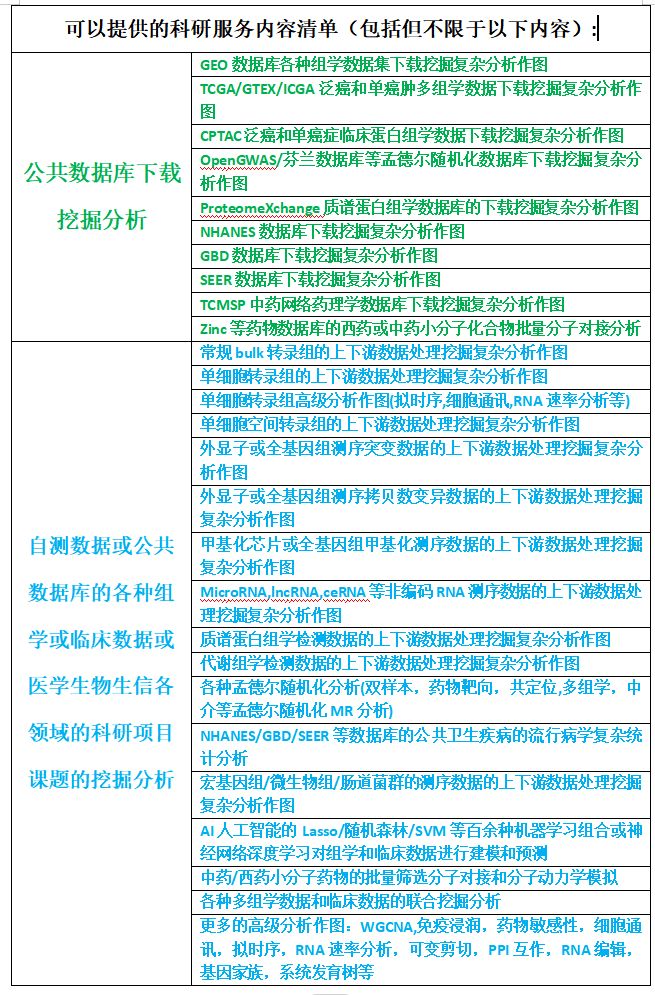
OmicsTools生信环境全自动化安装配置教程,代做生信分析和辅导
OmicsTools软件介绍和下载安装配置 软件介绍 我开发了一款本地电脑无限使用的零代码生信数据分析作软图神器电脑软件OmicsTools,旨在成为可以做各种医学生物生信领域科研数据分析作图的的全能科研软件,欢迎大家使用OmicsTools进行生物医学科研数据分析…...

鸿蒙HarmonyOS应用开发 探索 HarmonyOS Next-从开发到实战掌握 HarmonyOS Next 的分布式能力
鸿蒙心路旅程:探索 HarmonyOS Next-从开发到实战掌握 HarmonyOS Next 的分布式能力 HarmonyOS Next 是华为推出的全新一代操作系统,旨在进一步推动分布式技术的深度应用和生态融合。本文将从技术特点、应用场景入手,通过实战案例与代码示例&…...

二分模板题
题目传送门 主要思路: 暴力会tle n的3次方了然后 二分可以找中间然后去二分枚举两边 最后结果 ansa小于它的数*c大于它的数 注意要判断是否符合条件 即如果a的小于它的数还大于它就不成立 或者c的数小于它也不成立结果 要注意转long long ans(long long)tp1*tp2; …...

一篇文章掌握Git的基本原理与使用
目录 一、创建仓库 1.1 git init 1.2 git clone 二、工作区域与文件状态 三、添加和提交文件 3.1 git status 3.2 git add git rm --cached 3.3 git commit git log 四、版本回退 soft hard mixed 总结 五、查看差异 工作区与暂存区 工作区与本地仓库 暂存区…...

「Mac畅玩鸿蒙与硬件43」UI互动应用篇20 - 闪烁按钮效果
本篇将带你实现一个带有闪烁动画的按钮交互效果。通过动态改变按钮颜色,用户可以在视觉上感受到按钮的闪烁效果,提升界面互动体验。 关键词 UI互动应用闪烁动画动态按钮状态管理用户交互 一、功能说明 闪烁按钮效果应用实现了一个动态交互功能…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
