【scipy.sparse包】Python稀疏矩阵详解
【scipy.sparse包】Python稀疏矩阵
文章目录
- 【scipy.sparse包】Python稀疏矩阵
- 1. 前言
- 2. 导入包
- 3. 稀疏矩阵总览
- 4. 稀疏矩阵详细介绍
- 4.1 coo_matrix
- 4.2 dok_matrix
- 4.3 lil_matrix
- 4.4 dia_matrix
- 4.5 csc_matrix & csr_matrix
- 4.6 bsr_matrix
- 5. 稀疏矩阵的存取
- 5.1 用save_npz保存单个稀疏矩阵
- 6. 总结
- 7. 参考
1. 前言
-
数组和矩阵是数值计算的基础元素。目前为止,我们都是使用NumPy的ndarray数据结构来表示数组,这是一种同构的容器,用于存储数组的所有元素。
-
有一种特殊情况,矩阵的大部分元素都为零,这种矩阵被称为稀疏矩阵。对于稀疏矩阵,将所有零保存在计算机内存中的效率很低,更合适的方法是只保存非零元素以及位置信息。于是SciPy应运而生,为稀疏矩阵的表示及其线性代数运算提供了丰富易用的接口。
2. 导入包
SciPy中提供了稀疏矩阵模块scipy.sparse,为稀疏矩阵的表示及其线性代数运算提供了丰富易用的接口。
import scipy.sparse as sp
import scipy.sparse.linalg
import scipy.linalg as la
3. 稀疏矩阵总览
There are seven available sparse matrix types:1. csc_matrix: Compressed Sparse Column format2. csr_matrix: Compressed Sparse Row format3. bsr_matrix: Block Sparse Row format4. lil_matrix: List of Lists format5. dok_matrix: Dictionary of Keys format6. coo_matrix: COOrdinate format (aka IJV, triplet format)7. dia_matrix: DIAgonal format
- sp.coo_matrix(坐标的列表)描述:将非零值及其行列信息保存在一个列表。构造简单,添加元素方便,但访问元素效率低下;
- sp.lil_matrix(列表的列表):将每行的非零元素列索引保存在一个列表,将对应值保存在另一个列表。支持切片操作,但不方便进行数学运算;
- sp.dok_matrix(值的字典):将非零值保存在字典,非零值的坐标元组作为字典的键。构造简单,可快速添加删除元素,但不方便进行数学运算;
- sp.dia_matrix(对角矩阵):矩阵的对角线列表 。对于对角矩阵非常有效 ,但不适用非对角矩阵;
- sp.csc_matrix 和 sp.csr_matrix(压缩列格式和压缩行格式):将值与行列索引的数组一起存储。对于矩阵的向量乘法很高效,但构造相对复杂;
- sp.bsr_matrix(块稀疏矩阵):与CSR类似,用于具有稠密子矩阵的稀疏矩阵。对于此类特殊矩阵很高效,但不适用一般矩阵。
注意:
- 为了有效地构建矩阵,使用dok_matrix或者lil_matrix,lil_matrix类支持基本的切片和索引操作,语法与NumPy的arrays相似。
- COO格式也能有效率地构建矩阵。尽管与NumPy有许多相似性,但是强烈不建议使用NumPy的函数直接对稀疏矩阵格式进行操作,因为可能导致不正确的结果。如果将NumPy的函数用在这些矩阵上,首先检查SciPy在对应的稀疏矩阵类上有没有已经实现的操作,或者使用toarray()方法将稀疏矩阵对象转为NumPy的array。
- 实现乘法与转置操作,则转为CSC或CSR格式,lil_matrix格式是基于行的,所以转为为CSR比CSC更有效率。所有的转换在CSR,CSC和COO格式之间都是有效的,线性时间操作。
4. 稀疏矩阵详细介绍
4.1 coo_matrix
coo_matrix是最简单的存储方式。采用三个数组row、col和data保存非零元素的行下标,列下标与值。这三个数组的长度相同一般来说,coo_matrix主要用来创建矩阵,因为coo_matrix无法对矩阵的元素进行增删改等操作,一旦创建之后,除了将之转换成其它格式的矩阵,几乎无法对其做任何操作和矩阵运算。

为了创建sp.coo_matrix对象,需要创建非零值、行索引以及列索引的列表或数组,并将其传递给生成函数sp.coo_matrix。
values = [1, 2, 3, 4]
rows = [0, 1, 2, 3]
cols = [1, 3, 2, 0]
A = sp.coo_matrix((values, (rows, cols)), shape=[4, 4])
A

>>> A.toarray()
array([[1, 0, 0, 0],[0, 0, 0, 2],[0, 0, 3, 0],[4, 0, 0, 0]])
>>> type(A)
<class 'scipy.sparse.coo.coo_matrix'>
>>> type(A.toarray())
<class 'numpy.ndarray'>
SciPy的sparse模块中稀疏矩阵的属性大部分派生自NumPy的ndarray对象,同时也包括nnz(非零元素数目)和data(非零值)等属性。
A.shape, A.size, A.dtype, A.ndim
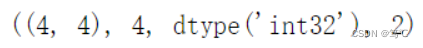
A.nnz, A.data
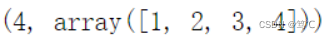
对于sp.coo_matrix对象,还可以使用row和col属性来访问底层的行列坐标数组。
A.row, A.col
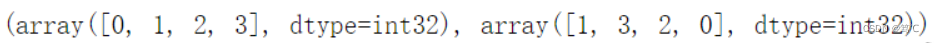
4.2 dok_matrix
dok_matrix适用的场景是逐渐添加矩阵的元素。dok_matrix的策略是采用字典来记录矩阵中不为0的元素。所以字典的key存的是记录元素的位置信息的元祖,value是记录元素的具体值。
>>> S = sparse.dok_matrix((5, 5), dtype=np.float32)
>>> for i in range(5):for j in range(5):S[i,j] = i+j # 更新元素
>>> S.toarray()
[[0. 1. 2. 3. 4.][1. 2. 3. 4. 5.][2. 3. 4. 5. 6.][3. 4. 5. 6. 7.][4. 5. 6. 7. 8.]]
- 优点:对于递增的构建稀疏矩阵很高效,比如定义该矩阵后,想进行每行每列更新值,可用该矩阵。当访问某个单元,只需要O(1)
- 缺点:不允许重复索引(coo中适用),但可以很高效的转换成coo后进行重复索引。
4.3 lil_matrix
lil_matrix适用的场景也是逐渐添加矩阵的元素。与dok不同,lil_matrix则是使用两个列表存储非0元素。data保存每行中的非零元素,rows保存非零元素所在的列。这种格式也很适合逐个添加元素,并且能快速获取行相关的数据。
>>> l = sparse.lil_matrix((4, 4))
>>> l[1, 1] = 1
>>> l[1, 3] =2
>>> l[2, 3] = 3
>>> l.toarray()
array([[0., 0., 0., 0.],[0., 1., 0., 2.],[0., 0., 0., 3.],[0., 0., 0., 0.]])
>>> l.data
array([list([]), list([1.0, 2.0]), list([3.0]), list([])], dtype=object)
>>> l.rows
array([list([]), list([1, 3]), list([3]), list([])], dtype=object)
- 优点:适合递增的构建成矩阵、转换成其它存储方式很高效、支持灵活的切片。
- 缺点:当矩阵很大时,考虑用coo、算术操作,列切片,矩阵向量内积操作慢。
4.4 dia_matrix
如果稀疏矩阵仅包含非0元素的对角线,则对角存储格式(DIA)可以减少非0元素定位的信息量。这种存储格式对有限元素或者有限差分离散化的矩阵尤其有效。dia_matrix通过两个数组确定: data和offsets。其中data对角线元素的值;offsets:第i个offsets是当前第i个对角线和主对角线的距离。data[k:]存储了offsets[k]对应的对角线的全部元素。例子如下:
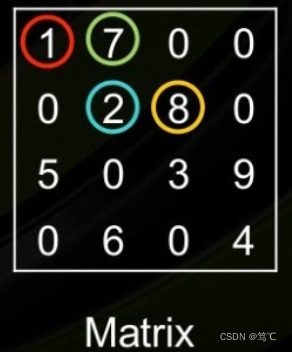
>>> data = np.array([[1, 2, 3, 4], [5, 6, 0, 0], [0, 7, 8, 9]])
>>> offsets = np.array([0, -2, 1])
>>> sparse.dia_matrix((data, offsets), shape=(4, 4)).toarray()
array([[1, 7, 0, 0],[0, 2, 8, 0],[5, 0, 3, 9],[0, 6, 0, 4]])
注意:offsets[0]=0表示第0个对角线与主对角线的距离为0,表示第0个对角线就是主对角线,data[0]就是第0个对角线的值。offsets[1]=-2表示第1个对角线与主对角线距离为-2,此时该对角线在主对角线的左下方,对角线上数值的数量为4-2=2,对应的值为data[1, :2+1],此时data[1, 3:]为无效的值,在构造对角稀疏矩阵时不起作用。offsets[2]=1表示第2个对角线与主对角线距离为1,此时该对角线在主对角线的右上方,对角线上数值的数量为4-1=3,对应的值为data[2, 1:],此时data[2, :1]为无效的值,在构造对角稀疏矩阵时不起作用。
4.5 csc_matrix & csr_matrix
csr_matrix是按行对矩阵进行压缩的,csc_matrix则是按列对矩阵进行压缩的。通过row_offsets,column_indices,data来确定矩阵。column_indices,data与coo格式的列索引与数值的含义完全相同,row_offsets表示元素的行偏移量。例子如下,
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],[0, 0, 3],[4, 5, 6]])
注意:indices和data分别表示列索引和数据,第 i 行的列索引存储在indices[indptr[i]:indptr[i+1]] 中,对应的值为data[indptr[i]:indptr[i+1]]。即第0行的列索引为indices[0:2]=[0,2],值为data[0:2]=[1,2];第1行的列索引为indices[2:3]=[2],值为data[2:3]=[3]…
CSR格式常用于读入数据后进行稀疏矩阵计算。
两者的优缺点互反:
-
CSR优点:高效的稀疏矩阵算术操作、高效的行切片、快速地矩阵向量内积操作;
-
CSR缺点:缓慢地列切片操作(可以考虑csc)、转换到稀疏结构代价较高(可以考虑lil,dok)。
-
CSC优点:高效的稀疏矩阵算术操作、高效的列切片、快速地矩阵向量内积操作(不如csr,bsr块);
-
CSC缺点:缓慢地行切片操作(可以考虑csr)、 转换到稀疏结构代价较高(可以考虑lil,dok)。
4.6 bsr_matrix
基于行的块压缩,通过row_offsets,column_indices,data来确定矩阵。与csr相比,只是data中的元数据由0维的数变为了一个矩阵(块),其余完全相同。
>>> indptr = np.array([0,2,3,6])
>>> indices = np.array([0,2,2,0,1,2])
>>> data = np.array([1,2,3,4,5,6]).repeat(4).reshape(6,2,2)
>>> bsr_matrix((data,indices,indptr), shape=(6,6)).todense()
matrix([[1, 1, 0, 0, 2, 2],[1, 1, 0, 0, 2, 2],[0, 0, 0, 0, 3, 3],[0, 0, 0, 0, 3, 3],[4, 4, 5, 5, 6, 6],[4, 4, 5, 5, 6, 6]])
优点:很类似于csr,更适合于矩阵的某些子矩阵很多值,在某些情况下比csr和csc计算更高效。
5. 稀疏矩阵的存取
5.1 用save_npz保存单个稀疏矩阵
>>> scipy.sparse.save_npz('sparse_matrix.npz', sparse_matrix)
>>> sparse_matrix = scipy.sparse.load_npz('sparse_matrix.npz')
稀疏矩阵存储大小比较:
a = np.arange(100000).reshape(1000,100)
a[10: 300] = 0
b = sparse.csr_matrix(a)
# 稀疏矩阵压缩存储到npz文件
sparse.save_npz('b_compressed.npz', b, True) # 文件大小:100KB
# 稀疏矩阵不压缩存储到npz文件
sparse.save_npz('b_uncompressed.npz', b, False) # 文件大小:560KB
# 存储到普通的npy文件
np.save('a.npy', a) # 文件大小:391KB
# 存储到压缩的npz文件
np.savez_compressed('a_compressed.npz', a=a) # 文件大小:97KB
对于存储到npz文件中的CSR格式的稀疏矩阵,内容为:
data.npy
format.npy
indices.npy
indptr.npy
shape.npy
6. 总结
- 加载数据文件时使用coo_matrix快速构建稀疏矩阵,然后调用to_csr()、to_csc()、to_dense()把它转换成CSR或稠密矩阵(numpy.matrix)。
- coo_matrix格式常用于从文件中进行稀疏矩阵的读写,而csr_matrix格式常用于读入数据后进行稀疏矩阵计算。
7. 参考
【1】https://blog.csdn.net/winycg/article/details/80967112
【2】https://blog.csdn.net/vor234/article/details/124935384
相关文章:

【scipy.sparse包】Python稀疏矩阵详解
【scipy.sparse包】Python稀疏矩阵 文章目录【scipy.sparse包】Python稀疏矩阵1. 前言2. 导入包3. 稀疏矩阵总览4. 稀疏矩阵详细介绍4.1 coo_matrix4.2 dok_matrix4.3 lil_matrix4.4 dia_matrix4.5 csc_matrix & csr_matrix4.6 bsr_matrix5. 稀疏矩阵的存取5.1 用save_npz保…...

从写下第1个脚本到年薪30W,我的自动化测试心路历程
我希望我的故事能够激励现在的软件测试人,尤其是还坚持在做“点点点”的测试人。 你可能会有疑问:“我也能做到这一点的可能性有多大?”因此,我会尽量把自己做决定和思考的过程讲得更具体一些,并尽量体现更多细节。 …...
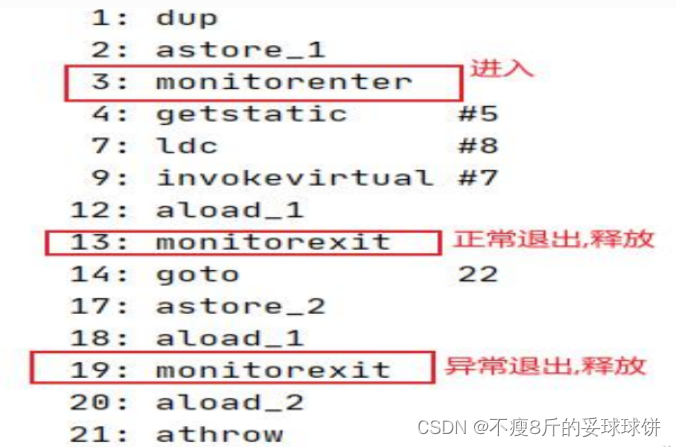
JAVA八股、JAVA面经
还有三天面一个JAVA软件开发岗,之前完全没学过JAVA,整理一些面经...... 大佬整理的:Java面试必备八股文_-半度的博客-CSDN博客 另JAVA学习资料:Java | CS-Notes Java 基础Java 容器Java 并发Java 虚拟机Java IO目录 int和Inte…...
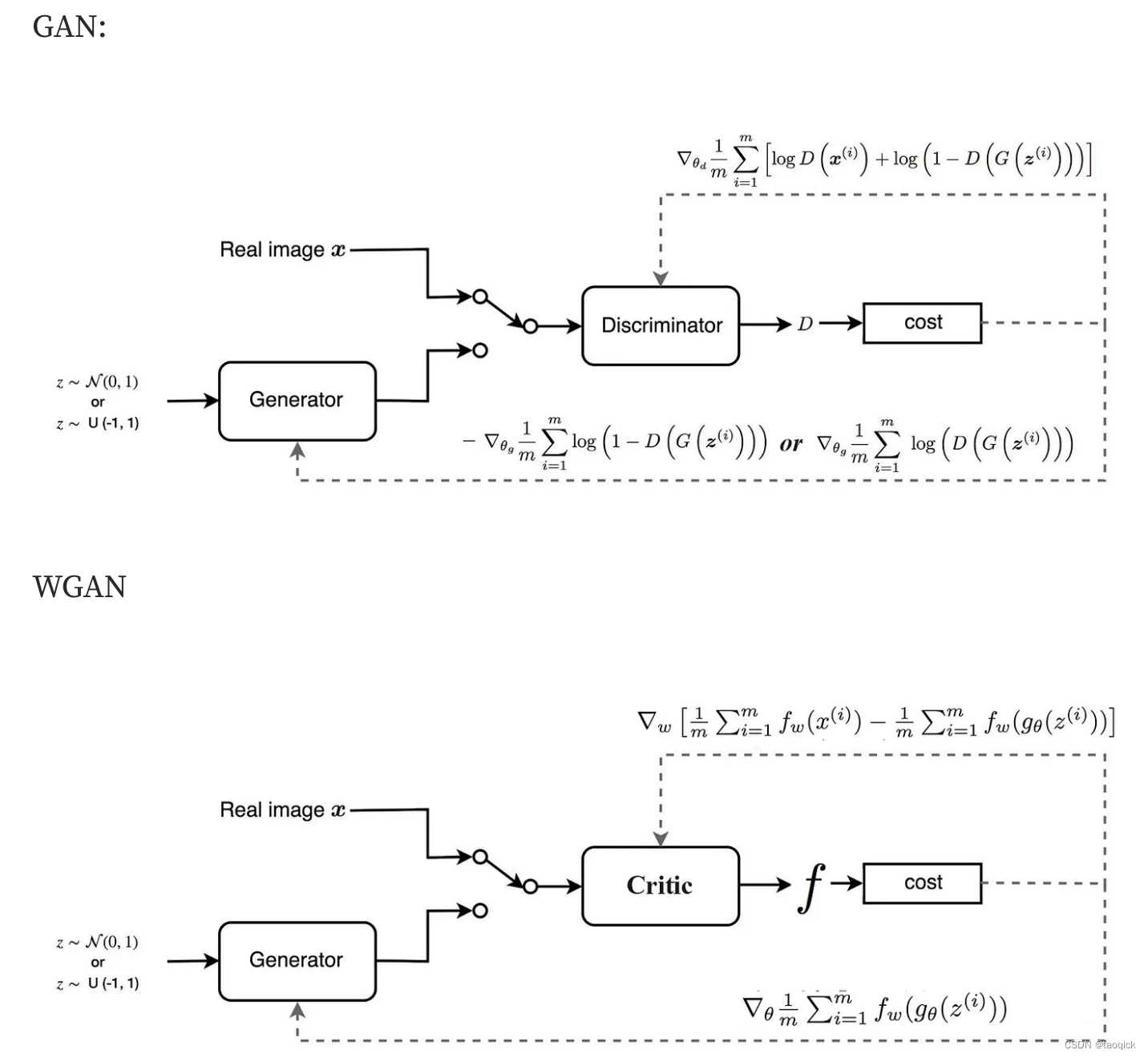
GAN系列基础知识
原始值函数 原始GAN的值函数是 minGmaxDV(D,G)Ex∼pdata(x)[logD(x)]Ez∼pz(z)[log(1−D(G(z)))]min_Gmax_DV(D,G) E_{x \sim p_{data}(x)}[logD(x)]E_{z \sim p_{z}(z)} [log(1-D(G(z)))]minGmaxDV(D,G)Ex∼pdata(x)[logD(x)]Ez∼pz(z)[log(1−D(G(z)))] 其中Ex…...
Linux/CenterOS 7.9配置汉化gitlab服务器
1.安装gitlab的依赖项 yum install -y curl openssh-server openssh-clients postfix cronie policycoreutils-python2.启动postfix,并设置为开机启动 systemctl start postfixsystemctl enable postfix3.防火墙和selinux的设置 setenforce 0systemctl stop fire…...

山洪灾害监测预警平台 山洪灾害监测预警系统解决方案 以人为本 科学防御
平升电子山洪灾害监测预警平台 山洪灾害监测预警系统解决方案,集信息采集、传输、分析和预警等功能于一体,实现预警信息及时、准确地上传下达,提升监测预警能力,使可能受灾区域能够及时采取措施,最大程度减少人员伤亡和…...

The Number Of ThreadPoolExecutor
序言整理下Java 线程池中线程数量如何设置的依据巨人肩膀:https://blog.csdn.net/weilaizhixing007/article/details/125955693https://blog.csdn.net/yuyan_jia/article/details/120298564#:~:text%E4%B8%80%E4%B8%AA%E7%BA%BF%E7%A8%8B%E6%B1%A0%E5%A4%84%E7%90%86%E8%AE%A1,…...

Linux(Linux各目录结构详解)
我们知道Linux系统是一个文件系统,它的文件系统就类似windows系统下的磁盘文件系统。 我们连接上一台linux系统的服务器。 输入命令 : ls / 我们可以看到 linux系统的根目录下有这些目录 bin boot data dev etc hbr home lib lib64 lostfoun…...

UART通讯简介
UART全称Universal AsynchronousReceiver/Transmitter,通用异步收发传输器。 一、工作原理 和其它串口一样,数据按照二进制从低位到高位一位一位的传输,能将要传输的数据在串行通信与并行通信之间加以转换,能够灵活地与外部设备进…...

80 90后表示真干不过,部门新来的00后已经把我卷奔溃了,不想干了····
都说00后躺平了,但是有一说一,该卷的还是卷。这不,刚开年我们公司来了个00后,工作没两年,跳槽到我们公司起薪18K,都快接近我了。 后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 …...

Python中2.x 与 3.x 版本区别?
Python 的 3.0 版本,常被称为 Python 3000,或简称 Py3k。相对于 Python 的早期版本,这是一个较大的升级。 为了不带入过多的累赘,Python 3.0 在设计的时候没有考虑向下相容。 许多针对早期 Python 版本设计的程式都无法在 P…...

性能指南笔记一
全面的性能 1.好处和效率之间的权衡在增加程序特性的过程 2.数据库永远是瓶颈,分布式系统的整体性能问题 我们当前的性能处于什么百分位? 是不是整体的性能属于下降的? 一开始就考虑可能性很小的性能问题? 3.吞吐量测试 TPS 每秒…...

es数据导入导出
使用elasticdump导入导出数据 一、安装elasticdump 终端中输入 1 npm install elasticdump -g -g表示全局可用,直接在终端输入 elasticdump --version,出现版本信息即表示安装成功,如下 1 2 C:\Users\T470s>elasticdump --version 6.3.3 …...

Python3入门教程||Python3 字符串||Python3 列表
Python3 字符串字符串(string,简写为str)是 Python 中最常用的数据类型之一。我们可以使用引号( 或 " )来创建字符串。创建字符串很简单,只要为变量分配一个值即可。例如:var1 Hello World!var2 "W3Cscho…...

API 的安全性
大家好。今天聊一个很重要但是大部分人不重视的API安全问题。api固有的范围和风险意味着它们需要一种不同的安全方法。应用程序编程接口(api)是现代应用程序的构建模块,它们的使用正在以惊人的速度增长。然而,随着使用的增加,风险也会增加。。…...

Linux驱动->设备树
1.定义 设备树(device tree是描述硬件信息的一种树形结构,设备书文件在linux内核启动后被内核解析。描述一个硬件设备信息的节点我们叫做设备节点,一个设备节点内部包含当前硬件的多个不同属性,相同节点不同 2.设备树的文件格式…...

一天一道力扣题
232. 用栈实现队列请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):实现 MyQueue 类:void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek()…...

算法leetcode|36. 有效的数独(rust重拳出击)
文章目录36. 有效的数独:样例 1:样例 2:提示:分析:题解:rustgoccpythonjava36. 有效的数独: 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效…...

都说爱有回音,这次情人节驱动人生宠你!
来了来了,它又来了——那个一波人狂欢,一波人孤单的节日。 眼看着身边人在订花订餐厅,选礼物,空气中弥漫着微妙的氛围,驱动哥脑海里只有明天下班的地铁挤不挤得过这群约会的人。 不过根据哥的观察,发现一个…...

npm安装依赖报错 npm code ERESOLVEnpm ERESOLVE unable to resolve dependency tree
在安装npm i vue-router (路由)时出现了这个错误。 npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: vue_test@0.1.0 npm ERR! Found: vue@2.6.14 npm ERR! node_modules/vue npm ERR! vue@"^2.6.…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
