后量子 KEM 方案:Kyber
参考文献:
- Bos J, Ducas L, Kiltz E, et al. CRYSTALS-Kyber: a CCA-secure module-lattice-based KEM[C]//2018 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 2018: 353-367.
- Avanzi R, Bos J, Ducas L, et al. Crystals-kyber[J]. NIST, Tech. Rep, 2017.
- Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory (TOCT), 2014, 6(3): 1-36.
文章目录
- Kyber
- Module-LWE
- IND-CPA PKE
- IND-CCA KEM
- KEY EXCHANGE
- 正确性分析
- 实例化
Kyber
Module-LWE
Kyber 基于 MLWE 问题,成为了唯一进入 NIST PQC 第 3 轮的 KEM 方案(一共 4 个方案,另外 3 个都是签名,其中 2 个也基于 MLWE,另外 1 个基于 Hash)。
MLWE 最早作为标准 LWE 与 Ring-LWE 的扩展 General LWE 出现在 BGV 方案中:分圆多项式环记做 Rq=Zq[X]/(Xn+1)R_q = Z_q[X]/(X^n+1)Rq=Zq[X]/(Xn+1),随机采样秘密向量 s∈Rqks \in R_q^ks∈Rqk,均匀随机采样 ai∈U(Rqk)a_i \in U(R_q^k)ai∈U(Rqk),计算 bi=aiTs+ei∈Rqb_i=a_i^Ts+e_i \in R_qbi=aiTs+ei∈Rq,输出 mmm 对样本 (ai,bi)∈Rqk×Rq(a_i,b_i) \in R_q^k \times R_q(ai,bi)∈Rqk×Rq
基于 MLWE 问题的密码方案,需要使得 m=km=km=k 以保证私钥的安全性。因此,按行排列,mmm 个 MLWE 样本可以写作 (A,b)∈Rqk×k×Rqk(A,b) \in R_q^{k \times k} \times R_q^k(A,b)∈Rqk×k×Rqk,其中 b=As+eb=As+eb=As+e
使用 MLWE 的一个优势是:改变安全级别时,只需调整矩阵规模 kkk 以及噪声规模 η\etaη,而环 RqR_qRq 不需要改变,因此可以代码复用,有利于软硬件优化。
IND-CPA PKE
Kyber 使用 Newhope-Simple 的思路,通过压缩密钥和密文来减小规模。对于 x∈Zqx \in \mathbb Z_qx∈Zq,进行 ddd 比特离散化:
Compress(x,d):=⌊2dq⋅x⌉(mod2d)Decompress(x,d):=⌊q2d⋅x⌉(modq)\begin{aligned} \text{Compress}(x,d) &:= \left\lfloor \dfrac{2^d}{q} \cdot x \right\rceil \pmod{2^d}\\ \text{Decompress}(x,d) &:= \left\lfloor \dfrac{q}{2^d} \cdot x \right\rceil \pmod{q}\\ \end{aligned} Compress(x,d)Decompress(x,d):=⌊q2d⋅x⌉(mod2d):=⌊2dq⋅x⌉(modq)
这可以被视为FHE中的“模切换”技术,引入了少量的(均匀)舍入噪声。
Kyber 的 PKE 方案与 Newhope 和 LAC 的几乎完全一样:

IND-CCA KEM
同样的,Kyber 也是用 Fujisaki–Okamoto transform 得到 CCA 安全的 KEM:

当解密错误时,并不输出 ⊥∉{0,1}256\perp \not \in \{0,1\}^{256}⊥∈{0,1}256,而是输出伪随机的 H(z,c)H(z,c)H(z,c),“隐式拒绝”。
KEY EXCHANGE
无身份认证的 KE 协议:

单方面身份认证的 KE 协议:

双向身份认证的 KE 协议:

正确性分析
在 CPA PKE 中,公钥的第二分量包含中心二项分布噪声和舍入噪声,
b=Decompress(Compress(A⋅s+e,d0),d0)=As+e+r0\begin{aligned} b &= \text{Decompress}(\text{Compress}(A \cdot s+e,d_0),d_0)\\ &= As+e+r_0\\ \end{aligned} b=Decompress(Compress(A⋅s+e,d0),d0)=As+e+r0
其中 s←RΨη1kns \leftarrow_R \Psi_{\eta_1}^{kn}s←RΨη1kn,e←RΨη2kne \leftarrow_R \Psi_{\eta_2}^{kn}e←RΨη2kn。在压缩时简单丢弃了低位比特,因此可以近似地认为舍入噪声是均匀的。令 l=⌈logq⌉l = \lceil \log q \rceill=⌈logq⌉,那么 r0←RU(R2l−d0k)r_0 \leftarrow_R U(R_{2^{l-d_0}}^k)r0←RU(R2l−d0k)
类似地,密文的第一分量中的噪声为:
c1=Decompress(Compress(AT⋅s′+e′,d1),d1)=AT⋅s′+e′+r1\begin{aligned} c_1 &= \text{Decompress}(\text{Compress}(A^T \cdot s'+e',d_1),d_1)\\ &= A^T \cdot s'+e'+r_1\\ \end{aligned} c1=Decompress(Compress(AT⋅s′+e′,d1),d1)=AT⋅s′+e′+r1
其中 s′←RΨη1kns' \leftarrow_R \Psi_{\eta_1}^{kn}s′←RΨη1kn,e′←RΨη2kne' \leftarrow_R \Psi_{\eta_2}^{kn}e′←RΨη2kn,r1←RU(R2l−d1k)r_1 \leftarrow_R U(R_{2^{l-d_1}}^k)r1←RU(R2l−d1k)
对于密文的第二分量,可以计算出它携带的噪声项:
c2=Decompress(Compress(bT⋅s′+e′′+Encode(m),d2),d2)=bT⋅s′+e′′+Encode(m)+r2=(As)Ts′+eTs′+r0Ts′+e′′+r2+Encode(m)\begin{aligned} c_2 &= \text{Decompress}(\text{Compress}(b^T \cdot s'+e''+ \text{Encode}(m),d_2),d_2)\\ &= b^T \cdot s'+e''+ \text{Encode}(m)+r_2\\ &= (As)^T s' + e^Ts' + r_0^Ts' + e'' + r_2 + \text{Encode}(m)\\ \end{aligned} c2=Decompress(Compress(bT⋅s′+e′′+Encode(m),d2),d2)=bT⋅s′+e′′+Encode(m)+r2=(As)Ts′+eTs′+r0Ts′+e′′+r2+Encode(m)
其中 e′′←RΨη2kne'' \leftarrow_R \Psi_{\eta_2}^{kn}e′′←RΨη2kn,r2←RU(R2l−d2k)r_2 \leftarrow_R U(R_{2^{l-d_2}}^k)r2←RU(R2l−d2k)。
解密步骤是 m←Decode(c2−c1T⋅s)m \leftarrow \text{Decode}(c_2 - c_1^T \cdot s)m←Decode(c2−c1T⋅s),我们可以计算出
c2−c1T⋅s=Encode(m)+(As)Ts′+eTs′+r0Ts′+e′′+r2−sTATs′−sTe′−sTr1=Encode(m)+(e+r0)Ts′−sT(e′+r1)+(e′′+r2)\begin{aligned} c_2 - c_1^T \cdot s =\,\,& \text{Encode}(m) + (As)^T s' + e^Ts' + r_0^Ts' \\ &+ e'' + r_2 - s^TA^Ts' - s^Te' - s^Tr_1\\ =\,\,& \text{Encode}(m) + (e+r_0)^Ts' - s^T(e'+r_1)+(e''+r_2) \end{aligned} c2−c1T⋅s==Encode(m)+(As)Ts′+eTs′+r0Ts′+e′′+r2−sTATs′−sTe′−sTr1Encode(m)+(e+r0)Ts′−sT(e′+r1)+(e′′+r2)
简记 E=∥(e+r0)Ts′−sT(e′+r1)+(e′′+r2)∥∞E = \|(e+r_0)^Ts' - s^T(e'+r_1)+(e''+r_2)\|_\inftyE=∥(e+r0)Ts′−sT(e′+r1)+(e′′+r2)∥∞ 为解密时的累积噪声规模。由于对消息采用了MSB编码方式,所以等式 m=Decode(Encode(m)+e)m=\text{Decode}(\text{Encode}(m)+e)m=Decode(Encode(m)+e) 成立的充要条件是 ∥e∥∞<⌊q/4⌉\|e\|_\infty < \lfloor q/4 \rceil∥e∥∞<⌊q/4⌉。
因此,我们需要选取合适的参数集,使得解密错误率足够小:
Δ:=Pr[E≥⌊q4⌉:(n,k,η1,η2,d0,d1,d2)]\Delta := \Pr\left[ E \ge \left\lfloor \dfrac{q}{4} \right\rceil:\,\, (n,k,\eta_1,\eta_2,d_0,d_1,d_2) \right] Δ:=Pr[E≥⌊4q⌉:(n,k,η1,η2,d0,d1,d2)]
实例化
在第三轮 NIST PQC 文档中,Kyber 的参数选取如下:

由于 q=3329=13×256+1q = 3329 = 13 \times 256+1q=3329=13×256+1,因此在 GF(q)GF(q)GF(q) 中存在 256256256 次本原单位根,从而可以支持 log128=7\log{128}=7log128=7 轮的“不完全的反循环NTT变换”,将环元素 f∈Rqf \in R_qf∈Rq 同构于 128128128 个长度为 222 的小多项式。注意 NTT 实现时采用 Montgomery 算法、 Barrett 算法,进行加速。
用到的对称原语(PRF, XOF, KDF, Hash)采用 FIPS-202 标准(SHA3):

相关文章:

后量子 KEM 方案:Kyber
参考文献: Bos J, Ducas L, Kiltz E, et al. CRYSTALS-Kyber: a CCA-secure module-lattice-based KEM[C]//2018 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 2018: 353-367.Avanzi R, Bos J, Ducas L, et al. Crystals-kyber[J]. NIST…...
2019年广东工业大学腾讯杯新生程序设计竞赛(同步赛)
同步赛链接 A-原初的信纸(最值,STL) 题意: 找 n 个数的最大值. 参考代码: void solve() {int n;std::cin >> n;std::vector<int> a(n);for (auto &c : a)std::cin >> c;std::cout << *max_element…...

生产Nginx现大量TIME-WAIT,连接耗尽,该如何处理?
背景说明: 在尼恩读者50交流群中,是不是有小伙伴问: 尼恩,生产环境 Nginx 后端服务大量 TIME-WAIT , 该怎么办? 除了Nginx进程之外,还有其他的后端服务如: 尼恩,生产环境…...
Linux服务器clang-13安装(环境变量配置)
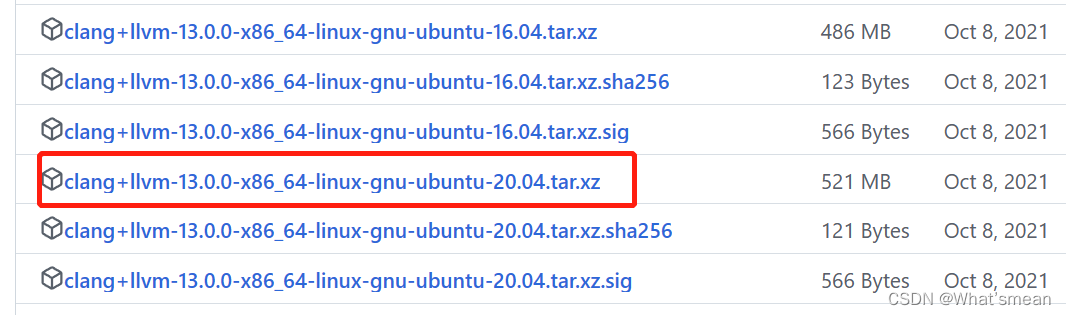
1.从llvm的github网址选择合适的release合适的运行平台进行下载,下载官方预编译的二进制压缩包。 2.将下载好的压缩包进行本地上传。 使用scp命令进行上传 scp -r -P 端口号 本地文件路径 服务器ID等:服务器上目标地址 3.解压(tar命令) 4.环境变量配…...
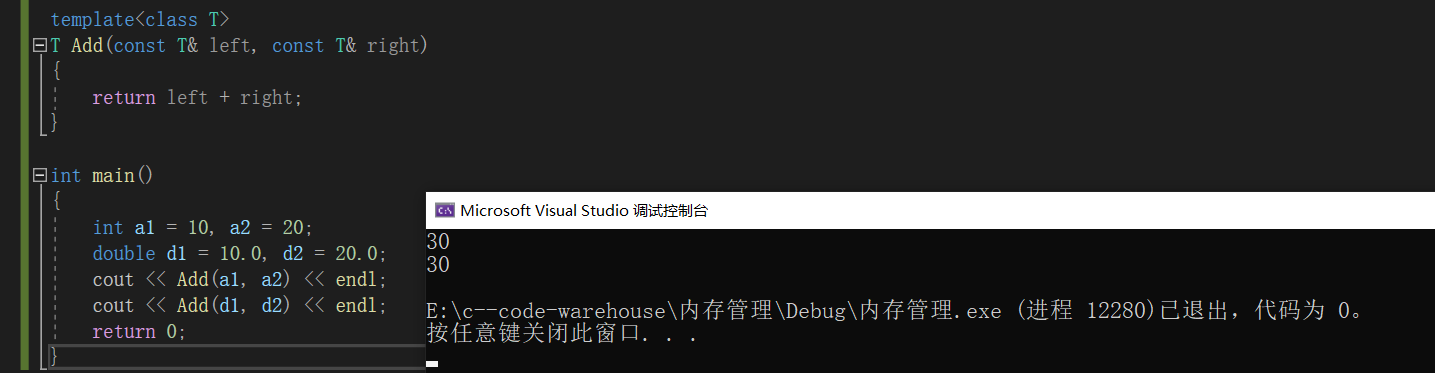
【C++】C/C++内存管理模板初阶
文章目录一、 C/C内存管理1. C/C内存分布2. C内存管理方式3. operator new与operator delete函数4. new和delete的实现原理5. 定位new表达式6. 常见面试题malloc/free和new/delete的区别内存泄漏二、模板初阶1. 泛型编程2. 函数模板3. 类模板一、 C/C内存管理 1. C/C内存分布 …...

笙默考试管理系统-index展示
public class PageList<T> : List<T> { public int PageIndex { get; private set; } //页索引 public int PageSize { get; private set; }//页大小 public int TotalPage { get; private set; }//总页数 public int TotalCo…...
前端基础知识6
谈谈你对语义化标签的理解语义化标签就是具有语义的标签,它可以清晰地向我们展示它的作用和用途。 清晰的代码结构:在页面没有css的情况下,也能够呈现出清晰的代码内容 有利于SEO: 爬虫依赖标签来确定关键字的权重,因此可以和搜索…...

【项目精选】智慧物业管理系统
点击下载源码 1、 选题的背景、研究目的和意义 1)选题的背景 智慧物业是物业发展的必然趋势,是物业管理的一种新理念,是 新形势下社会管理创新的一种新模式。 随着人工智能、大数据、互联网等高新技术的发展,物业管理企 业先后试…...
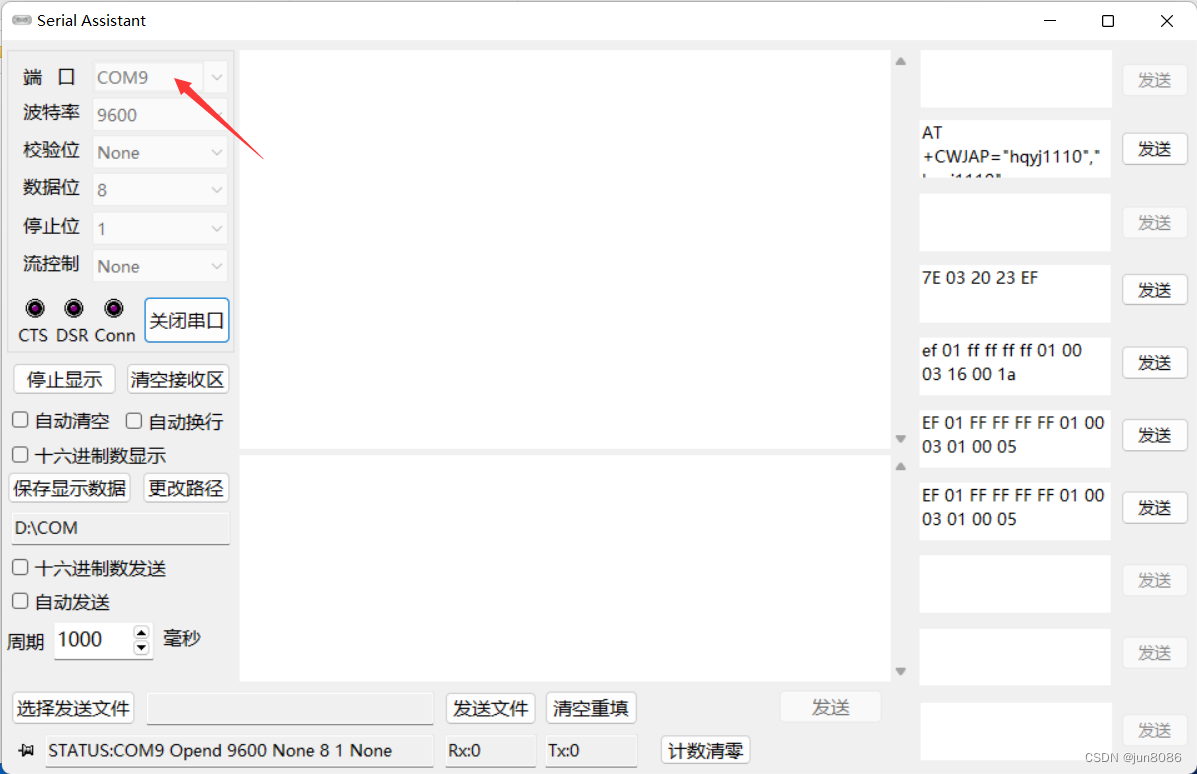
解决HC-05/HC06等蓝牙模块的调试问题
解决HC-05/HC06等蓝牙模块的调试问题问题:1.无法使用USB转串口工具设置HC-05等蓝牙模块,具体问题是:发送AT指令,无回复;2.电脑如何连接HC-05模块,与模块通信(具体场景:HC-05模块的串…...

dfs(八)数字的全排列 (含有重复项与非重复项)
如果每个数字任意取的话。就不需要加book标志位 没有重复项数字的全排列_牛客题霸_牛客网 描述 给出一组数字,返回该组数字的所有排列 例如: [1,2,3]的所有排列如下 [1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1]. (以数字在数组中的位…...

基于微信小程序的医院挂号系统小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...

工程经验:残差连接对网络训练的巨大影响
文章目录1、没有使用残差连接的网络难以训练2、loss 不下降的原因3、使用了残差连接的网络可以高效训练1、没有使用残差连接的网络难以训练 经典的 SegNet 网络结构如下: 在使用上图所示的 SegNet 作为噪声预测网络训练扩散模型(DDPM)时&…...

靓号管理-搜索
搜索手机号: 最后一条就是使用的关键mobile__contains 使用字典: 后端的逻辑: """靓号列表"""data_dict {}search_data request.GET.get(q, "")# 根据关键字进行搜索,如果关键字存在&…...
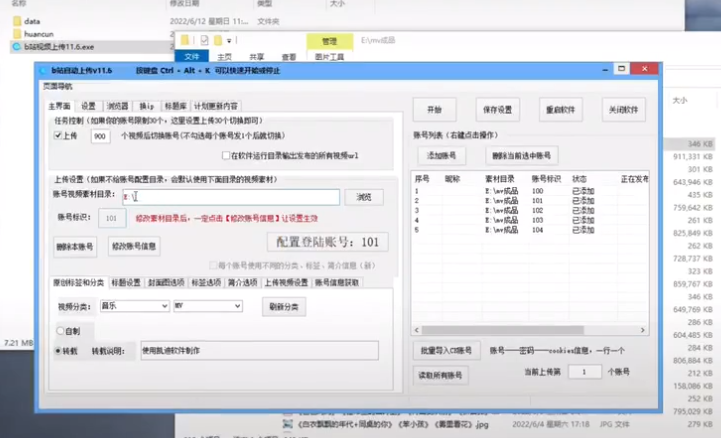
B站发帖软件哪个好用?好用的哔哩哔哩发帖工具
B站发帖软件哪个好用?好用的哔哩哔哩发帖工具#发帖软件#哔哩哔哩发帖#视频发布软件 登录成功之后,进入到这样一个界面,默认情况下是这个样子的,我们在这里输入一下我们的一个文件夹的路径,输入到这里,点击添加账号&a…...

docker
docker ps docker images 拉取ubuntu镜像 docker pull ubuntu 启动 docker start podid 进入bash界面 docker exec -it podid /bin/bash 安装sudo apt-get install sudo 更新使配置生效 sudo apt update 安装vim apt-get install vim 安装中文包 sudo apt-get i…...
Django by Example·第三章|Extending Your Blog Application@笔记
Django by Example第三章|Extending Your Blog Application笔记 之前已经写过两章内容了,继续第三章。第三章继续对博客系统的功能进行拓展,其中将会穿插一些重要的技术要点。 部分内容引用自原书,如果大家对这本书感兴趣 请支持原版Django …...

23.2.13 Drive development 设备树信息解析相关代码
1.练习课上代码 2.把设备树信息解析相关函数按照自己的理解发布CSDN 3.复习中断相关内核 IO多路复用---epoll 核心内容:一棵树一个链表三个方法 epoll会将要监听的事件文件描述符添加到内核里一颗红黑树上,当有事件发生,epoll会调用回调函数…...

智能工厂以MES系统为基础,实现"信息化减人,自动化换人"
MES是一种生产信息化的管理系统,它适用于制造业的车间实施层面。MES能够为企业提供生产数据、项目看板、库存、成本、工装、生产计划、计划排程、质量、人力资源、采购、生产过程控制、底层数据集成分析、上层数据集成分解等管理模块,为企业打造一个扎实…...

【数据挖掘实战】——电力窃漏电用户自动识别
【数据挖掘实战】——电力窃漏电用户自动识别一、背景和挖掘目标二、分析方法与过程1、初步分析2、数据抽取3、探索分析4、数据预处理5、构建专家样本三、构建模型1、构建窃漏电用户识别模型2、模型评价3、进行窃漏电诊断拓展思考项目代码地址:https://gitee.com/li…...
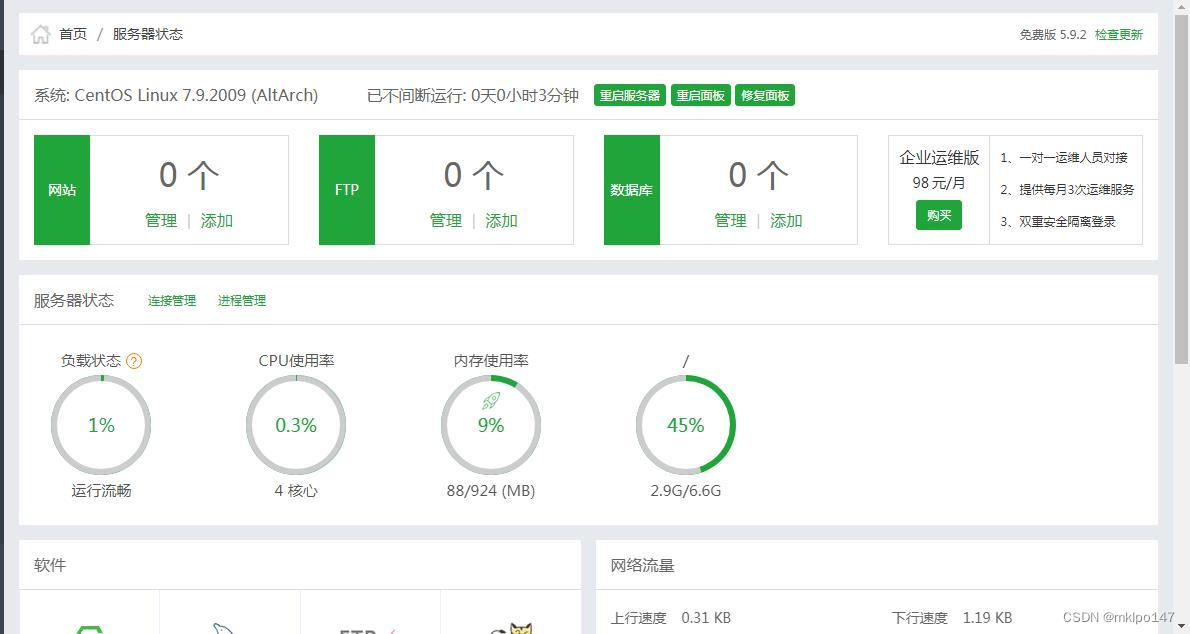
树莓派 安装 宝塔linux面板5.9. 2023-2-13
一.环境 1.硬件环境: 树莓派3b , 8GB tf卡 ,micro usb电源 2.网络环境: 网线直连路由器 , 可访问互联网 3.软件环境: 树莓派操作系统 CentOS-Userland-7-armv7hl-RaspberryPI-Minimal-2009-sda(linux) 系统刻录工具 Win32DiskImager (win) ip扫描工具 Adv…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
