定位,用最通俗易懂的方法2:TDOA与对应的CRLB
二郎就不设置什么VIP可见啥的了,这样大家都能看到。
如果觉得受益,可以给予一些打赏,也算对原创的一些鼓励,谢谢。
钱的用途:1)布施给他人;2)二郎会有更多空闲时间写教程
起因:
二郎虽然也对TDOA和CRLB有所了解,而且写了一些相关的代码,但是还是觉得不够透彻,不能非常好地去教给别人,所以,本专题,二郎就用代码和解释并行,一步一步和大家说明,公式是怎么代码实现的,以及怎么仿真的。
论文《A Simple and Efficient Estimator for Hyperbolic Location》
仿真:
| 1)初始配置 |
clc; close all; clear all; warning off; % 程序初始化。
L = 10e3; % 蒙特卡洛运行次数。
randn('seed',0); % 初始化随机数生成器。uo = [-50 250]'; % 真实源位置。x = [0 -5 4 -2 7 -7 2 -4 3 1]; % 真实传感器位置矩阵。
y = [0 8 6 4 3 5 5 2 3 8];
S = [x; y];M = size(S,2); % 传感器数量。
N = size(S,1); % 定位维度。ro = sqrt(sum((uo*ones(1,M)-S).^2))'; % 真实源-传感器的距离
rdo = ro(2:end)-ro(1); % 距离差,其他距离与第一个距离的差R = (eye(M-1)+ones(M-1))/2; % TDOA 的协方差结构论文对应:
1)距离差

2)协方差结构
论文原文

matlab运行结果

| 2)噪声变化配置 |
NsePwrVecdB = -60:4:-24; % 改变测量噪声水平fprintf('模拟进行中');
for nseIdx = 1:length(NsePwrVecdB), % 改变测量噪声水平fprintf('。');nsePwr = 10^(NsePwrVecdB(nseIdx)/10);Q = nsePwr * R; % TDOA(范围差)噪声的协方差矩阵



这里Q = nsePwr * R; 是噪声的线性功率值乘以单位协方差矩阵,构建出实际的协方差矩阵。
| 3)CRLB |
crlb(nseIdx) = trace(TDOALocCRLB(S,uo,Q));
用迹是把x,y,z方向的误差方差相加
function [CRLB] = TDOALocCRLB(SensorPositions, SourceLocation, Q)
% SensorPositions: (Dim x M) 矩阵,每一列是一个传感器的位置,第一列是参考传感器
% SourceLocation: (Dim x 1) 源位置
% Q: TDOA(范围差)向量的协方差矩阵
% CRLB: (Dim x Dim) 估计源定位的 CRLB 矩阵% 通过输入我们就能看出,求CRLB是和传感器位置、源位置、协方差矩阵有关的M = length(Q) + 1;if (M < size(SensorPositions, 1) + 2)fprintf('传感器数量至少应为 %d\n', size(SensorPositions, 1) + 2);return;
end;if (rank(SensorPositions) < size(SensorPositions, 1))disp('传感器不应位于同一平面或直线上!');return;
endS = SensorPositions;
u = SourceLocation;M = size(SensorPositions, 2);
ro = sqrt(sum((u * ones(1, M) - S).^2)); %传感器和声源的距离d_u = (S(:, 2:end) - u * ones(1, M - 1))' ./ (ro(2:end)' * ones(1, size(S, 1))) ...- ones(M - 1, 1) * ((S(:, 1) - u)' / ro(1));J = d_u' * inv(Q) * d_u; % FIM
CRLB = inv(J);
论文对应:
1)Gt
d_u = (S(:, 2:end) - u * ones(1, M - 1))' ./ (ro(2:end)' * ones(1, size(S, 1))) ...- ones(M - 1, 1) * ((S(:, 1) - u)' / ro(1));

对应-Gt,这个负号其实没关系,因为有两个,相当于负负得正,还是一样的。
2)公式求解
c是信号传播速度,由于使用的r,不涉及速度,因此c=1。
J = d_u' * inv(Q) * d_u; % FIM
CRLB = inv(J);

我们这里再重新体验一遍CRLB的推导过程
①构建测量值的似然函数,这里测量值是r

②对对数似然函数进行求导

③构建zp的CRLB,对数似然函数的求导的积求期望

④得到FIR函数的形式后求逆,得到CRLB

| 4)求TDOA的过程---蒙特卡洛 |
SimulationMSE = 0;
for k = 1 : L, % 蒙特卡洛模拟。rdNse = sqrt(nsePwr/2) * randn(M,1);rd = rdo + rdNse(2:end)-rdNse(1); % 噪声源 TDOAs(范围差)。u = TDOALoc(S,rd,Q);SimulationMSE = SimulationMSE + norm(u-uo,2)^2; %多次计算的误差平方累加
end;
mse(nseIdx) = SimulationMSE/L;
S i = ( x i − x 0 ) 2 + ( y i − y 0 ) 2 S_i = (x_i - x_0)^2+(y_i - y_0)^2 Si=(xi−x0)2+(yi−y0)2
r e s u l t = ( S 1 + S 2 + … … + S n ) / N result = (S_1+S_2+……+S_n)/N result=(S1+S2+……+Sn)/N
| 5)求TDOA的过程---两步法---第一步 |
function [SourceLocation] = TDOALoc(S, r, Q)
% S: (Dim x M) 矩阵,每一列是一个传感器的位置,第一列是参考传感器,M 是传感器的数量,至少应为 Dim+2
% r: (M-1) x 1 的 TDOA 测量值乘以信号传播速度
% Q: r 向量的协方差矩阵
% SourceLocation: 估计的源位置RptCnt = 1; % 第一阶段重新计算 W1 的重复次数M = length(r) + 1;R = sqrt(sum(S.^2))';%=========== 构建相关向量和矩阵 ============
h1 = r.^2 - R(2:end).^2 + R(1)^2;
G1 = -2 * [S(:, 2:end)' - ones(M-1, 1) * S(:, 1)', r];%============= 第一阶段 ===================================
B = eye(M-1);
W1 = inv(B * Q * B');
u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;for j = 1:max(1, RptCnt),ri_hat = sqrt(sum((S - u1(1:end-1) * ones(1, M)).^2));B = 2 * diag(ri_hat(2:M)); W1 = inv(B * Q * B');u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;
endu1p = u1 - [S(:, 1); 0];
程序对应
1)构建相关向量和矩阵
%=========== 构建相关向量和矩阵 ============
h1 = r.^2 - R(2:end).^2 + R(1)^2;
G1 = -2 * [S(:, 2:end)' - ones(M-1, 1) * S(:, 1)', r];





2)初始迭代
B = eye(M-1);
W1 = inv(B * Q * B');
u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;


这是初始迭代,我们的权重设置的是对角线矩阵,也就是第一次只和协方差矩阵有关
3)获得初始的u1,然后完成权重的获取
for j = 1:max(1, RptCnt),ri_hat = sqrt(sum((S - u1(1:end-1) * ones(1, M)).^2));B = 2 * diag(ri_hat(2:M)); W1 = inv(B * Q * B');u1 = inv(G1' * W1 * G1) * G1' * W1 * h1;
end
这里有点差别,它没有用 r i 1 r_{i1} ri1,而是直接用声源的 x x x和 y y y,获得距离,进而按照距离进行加权


| 6)求TDOA的过程---两步法---第二步 |
u1p = u1 - [S(:, 1); 0];
%========== 第二阶段 =====================================
h2 = u1p.^2;
G2 = [eye(length(u1p) - 1); ones(1, length(u1p) - 1)];B2 = 2 * diag(u1p);
W2 = inv(B2') * (G1' * W1 * G1) * inv(B2);
u2 = inv(G2' * W2 * G2) * G2' * W2 * h2;



计算出来的结果是平方的形式,需要利用之前求的结果,给出正负号
%=========== 映射 ========================================
SourceLocation = sign(diag(u1p(1:length(u2)))) * sqrt(abs(u2)) + S(:, 1);
%============================================================
至此,完成了求解,之后可以展示结果
结果展示:
mse(nseIdx) = SimulationMSE/L;
end;
fprintf('\n');% 绘制结果。
figure(1); plot(NsePwrVecdB/2,10*log10(mse),'xk','MarkerSize',8); hold on;
plot(NsePwrVecdB/2,10*log10(crlb),'k'); grid on; hold off;xlabel('10 log(c\sigma)');
ylabel('10 log(MSE)');
legend('新方法','CRLB');
ylim([0 60]);

相关文章:

定位,用最通俗易懂的方法2:TDOA与对应的CRLB
二郎就不设置什么VIP可见啥的了,这样大家都能看到。 如果觉得受益,可以给予一些打赏,也算对原创的一些鼓励,谢谢。 钱的用途:1)布施给他人;2)二郎会有更多空闲时间写教程 起因&…...

Linux第一课:c语言 学习记录day06
四、数组 冒泡排序 两两比较,第 j 个和 j1 个比较 int a[5] {5, 4, 3, 2, 1}; 第一轮:i 0 n:n个数,比较 n-1-i 次 4 5 3 2 1 // 第一次比较 j 0 4 3 5 2 1 // 第二次比较 j 1 4 3 2 5 1 // 第三次比较 j 2 4 3 2 1 5 // …...

ExplaineR:集成K-means聚类算法的SHAP可解释性分析 | 可视化混淆矩阵、决策曲线、模型评估与各类SHAP图
集成K-means聚类算法的SHAP可解释性分析 加载数据集并训练机器学习模型 SHAP 分析以提取特征对预测的影响 通过混淆矩阵可视化模型性能 决策曲线分析 模型评估(多指标和ROC曲线的目视检查) 带注释阈值的 ROC 曲线 加载 SHAP 结果以进行下游分析 与…...

2025年第三届“华数杯”国际大学生数学建模竞赛A题题目
问题A:他能游得更快吗? 背景介绍 在2024年巴黎奥运会上,中国游泳运动员潘展乐凭借出色的表现成为全球瞩目的焦点。年仅19岁的他在男子100米自由泳比赛中以46秒40 的成绩夺冠,并创造了自己保持的世界纪录。在男子4100米混合泳接力…...
)
用c实现C++类(八股)
在 C 语言中,虽然没有内建的面向对象编程(OOP)特性(如封装、继承、多态),但通过一些编程技巧,我们仍然可以模拟实现这些概念。下面将用通俗易懂的方式,逐步介绍如何在 C 中实现封装、…...

【C++多线程编程:六种锁】
目录 普通互斥锁: 轻量级锁 独占锁: std::lock_guard: std::unique_lock: 共享锁: 超时的互斥锁 递归锁 普通互斥锁: std::mutex确保任意时刻只有一个线程可以访问共享资源,在多线程中常用于保…...

【Javascript Day5】for循环及典型案例
for 循环 // 语法: for( 开始 ; 结束 ; 步长 ){ 循环体 } // for( var i 循环初始值 ; i的循环范围 ; i的增加或减少规则 ){ 循环体 } // 死循环 // for(;;){ // console.log("for循环"); // } // 循环打…...

#渗透测试#网络安全#一文了解什么是shell反弹!!!
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

《解锁图像的语言密码:Image Caption 开源神经网络项目全解析》
《解锁图像的语言密码:Image Caption 开源项目全解析》 一、开篇:AI 看图说话时代来临二、走进 Image Caption 开源世界三、核心技术拆解:AI 如何学会看图说话(一)深度学习双雄:CNN 与 RNN(二&a…...

抢占欧洲电商高地,TikTok 运营专线成 “秘密武器”
在当今数字化浪潮席卷全球的时代,社交媒体平台已成为商业拓展的关键阵地,TikTok 更是其中的闪耀新星。近日,一则重磅消息引发行业关注:TikTok 正计划于 2025 年初进军荷兰电商市场。这一战略布局,不仅彰显了 TikTok 对…...

人工智能-数据分析及特征提取思路
1、概况 基于学生行为数据预测是否涉黄、涉黑等。 2.数据分析 数据分析的意义包括得到数据得直觉、发掘潜在的结构、提取重要的变量、删除异常值、检验潜在的假设和建立初步的模型。 2.1数据质量分析 2.1.1数据值分析 查看数据类型: 首先明确各字段的数据类型…...

2024 China Collegiate Programming Contest (CCPC) Zhengzhou Onsite 基础题题解
今天先发布基础题的题解,明天再发布铜牌题和银牌题的题解 L. Z-order Curve 思路:这题目说了,上面那一行,只有在偶数位才有可能存在1,那么一定存在这样的数,0 ,1,100, 10000,那么反之,我们的数…...

halcon3d 如何计算平面法向量!确实很简单
这个问题其实一直困扰了我很长时间,之前是怎么算的呢 对于一个平面,我会先求它的fit_primitives_object_model_3d去将它拟合,接下来用surface_normals_object_model_3d 算子生成它的法线,后用get_object_model_3d_params (ObjectModel3DNormals, ‘point_normal_x’, GenP…...
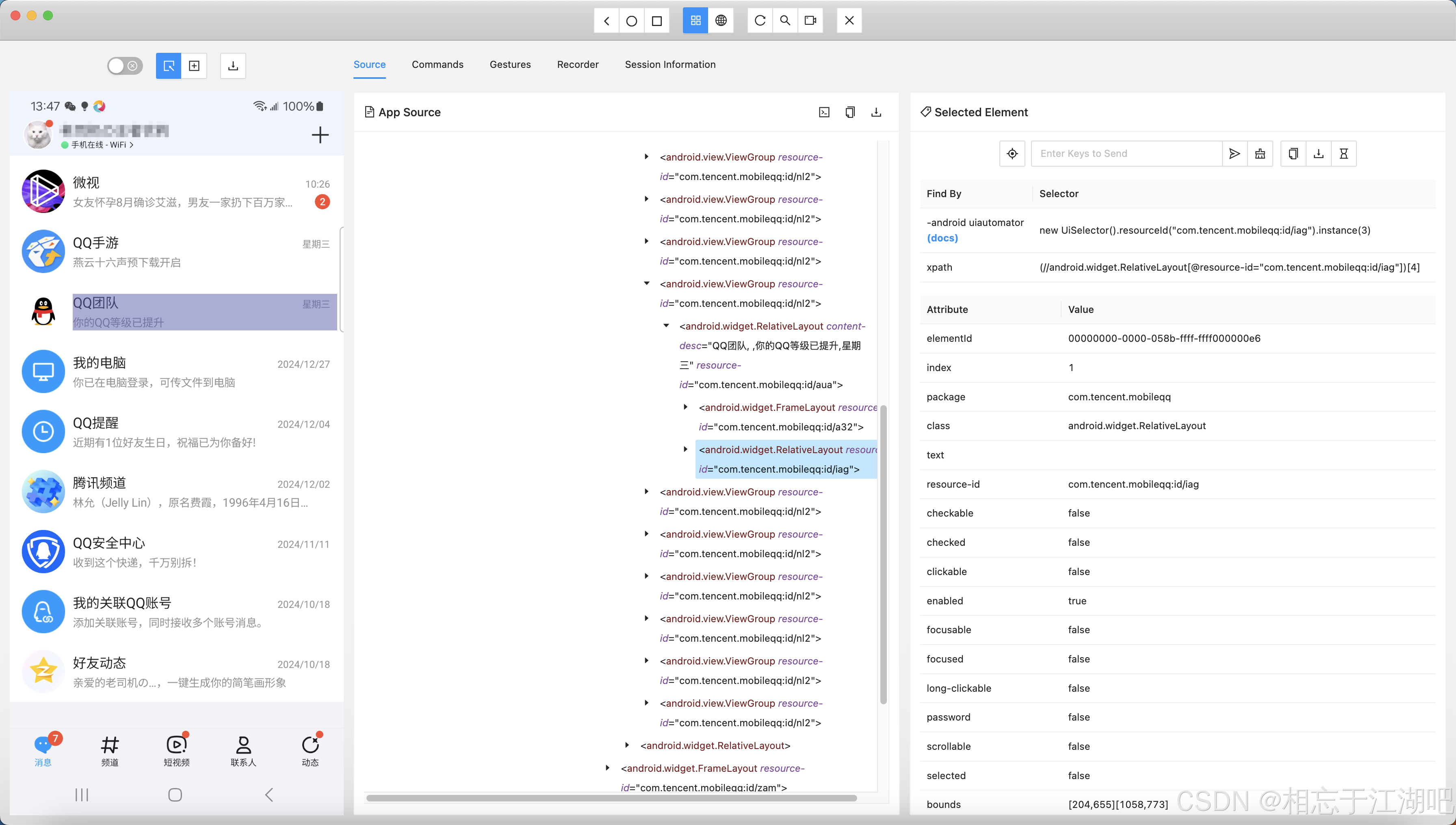
浅尝Appium自动化框架
浅尝Appium自动化框架 Appium自动化框架介绍Appium原理Appium使用安装平台驱动实战 坑 Appium自动化框架介绍 Appium 是一个开源的自动化测试框架,最初设计用于移动应用的测试,但现在它也扩展了对桌面端应用的支持。Appium 使得自动化测试变得更加简单&…...

网络安全测评技术与标准
网络安全测评概况 网络安全测评是网络信息系统和IT技术产品的安全质量保障。本节主要阐述网络安全测评的概念,给出网络安全测评的发展状况。 18.1.1 网络安全测评概念 网络安全测评是指参照一定的标准规范要求,通过一系列的技术和管理方法,获…...
【经典神经网络架构解析篇】【1】LeNet网络详解:模型结构解析、优点、实现代码
《------往期经典推荐------》 一、AI应用软件开发实战专栏【链接】 项目名称项目名称1.【人脸识别与管理系统开发】2.【车牌识别与自动收费管理系统开发】3.【手势识别系统开发】4.【人脸面部活体检测系统开发】5.【图片风格快速迁移软件开发】6.【人脸表表情识别系统】7.【…...

KGA:AGeneral Machine Unlearning Framework Based on Knowledge Gap Alignment
文章目录 摘要1 引言2 相关工作3 符号与定义4 我们的 KGA 框架4.1 KGA框架知识差距对齐目标 4.2 KGA在自然语言处理任务中的应用文本分类机器翻译响应生成 5 实验设置数据集评估指标参数设置比较方法 6 实验结果6.1 主要比较结果6.2 KGA 的优越性分析降低语言模型概率比较 6.3 …...

GelSight Mini视触觉传感器凝胶触头升级:增加40%耐用性,拓展机器人与触觉AI 应用边界
马萨诸塞州沃尔瑟姆-2025年1月6日-触觉智能技术领军企业Gelsight宣布,旗下Gelsight Mini视触觉传感器迎来凝胶触头的更新。经内部测试,新Gel凝胶触头耐用性提升40%,外观与触感与原凝胶触头保持一致。此次升级有效满足了客户在机器人应用中对设…...

springboot整合admin
1. 添加依赖 首先,在你的admin服务端pom.xml文件中添加Spring Boot Admin的依赖: <dependency><groupId>de.codecentric</groupId><artifactId>spring-boot-admin-starter-server</artifactId><version>2.5.4<…...

OS--常见的网络模型(包含IO多路复用的原理)
网络模型 IO模型主要就是用户空间和内核空间数据交换的形式。 IO模型 阻塞 I/O 模型(Blocking I/O) 应用程序发起 I/O 请求后,会被阻塞,直到 I/O 操作完成。 非阻塞 I/O 模型(Non-blocking I/O) 应用程序…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
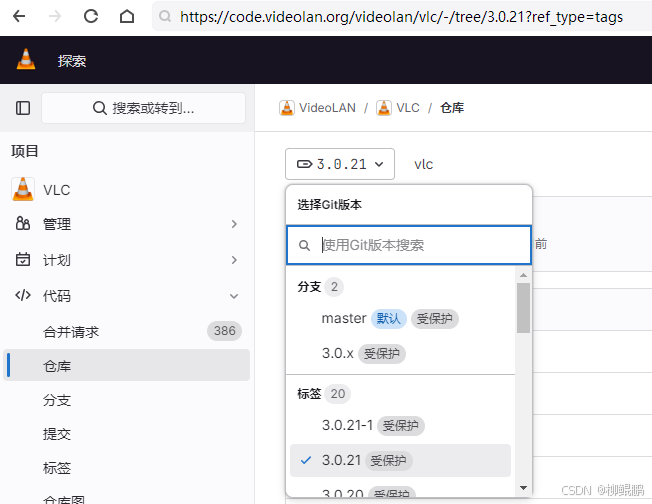
LINUX编译vlc
下载 VideoLAN / VLC GitLab 选择最新的发布版本 准备 sudo apt install -y xcb bison sudo apt install -y autopoint sudo apt install -y autoconf automake libtool编译ffmpeg LINUX FFMPEG编译汇总(最简化)_底部的附件列表中】: ffmpeg - lzip…...

信息系统分析与设计复习
2024试卷 单选题(20) 1、在一个聊天系统(类似ChatGPT)中,属于控制类的是()。 A. 话语者类 B.聊天文字输入界面类 C. 聊天主题辨别类 D. 聊天历史类 解析 B-C-E备选架构中分析类分为边界类、控制类和实体类。 边界…...

详解鸿蒙Next仓颉开发语言中的动画
大家上午好,今天来聊一聊仓颉开发语言中的动画开发。 仓颉中的动画通常有两种方式,分别是属性动画和显示动画,我们今天以下面的加载动画为例,使用显示动画和属性动画分别实现一下,看看他们有什么区别。 显示动画 显示…...
