Python贪心
贪心
- 贪心:把整体问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直至所有步骤结束;每个步骤不会影响后续步骤
- 核心性质:每次采用局部最优,最终结果就是全局最优
- 如果题目满足上述核心性质,则可以采用贪心进行求解
如何判断是否能用贪心?
- 最优子结构性质:当一个问题的最优解包含子问题的最优解,则称之为具有最优子结构性质。
- 贪心性质选择:可以通过局部最优的选择得到全局最优
具体问题如何做?
- 经验性积累各种类型的贪心
- 举反例
经典贪心
石子合并问题
石子合并问题:每次选择最小的两个
利用堆:heapq
题目描述
在很久很久以前,有 n n n 个部落居住在平原上,依次编号为 1 1 1 到 n n n。第 i i i 个部落的人数为 t i t_i ti。
有一年发生了灾荒。年轻的政治家小蓝想要说服所有部落一同应对灾荒,他能通过谈判来说服部落进行联合。
每次谈判,小蓝只能邀请两个部落参加,花费的金币数量为两个部落的人数之和,谈判的效果是两个部落联合成一个部落(人数为原来两个部落的人数之和)。
输入描述
输入的第一行包含一个整数 n n n,表示部落的数量。
第二行包含 n n n 个正整数,依次表示每个部落的人数。
其中, 1 ≤ n ≤ 1000 , 1 ≤ t i ≤ 1 0 4 1≤n≤1000,1≤t_i≤10^4 1≤n≤1000,1≤ti≤104。
输出描述
输出一个整数,表示最小花费。
import heapq
n = int(input())
a = list(map(int, input().split()))# 把a转化为堆
heapq.heapify(a)
ans = 0
while len(a) >= 2:x = heapq.heappop(a)y = heapq.heappop(a)heapq.heappush(a, x + y)ans += x + y
print(ans)
分箱问题
每组最多两件,价值之和不超过 w w w
尽可能不浪费空间:大的和小的凑在一起
题目描述
元旦快到了,校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得的纪念品价值相对均衡,他要把购来的纪念品根据价格进行分组,但每组最多只能包括两件纪念品,并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品,乐乐希望分组的数目最少。
你的任务是写一个程序,找出所有分组方案中分组数最少的一种,输出最少的分组数目。
输入描述
第 1 1 1 行包括一个整数 w ( 80 ≤ w ≤ 200 ) w (80≤w≤200) w(80≤w≤200),为每组纪念品价格之和的上限。
第 2 2 2 行为一个整数 n ( 1 ≤ n ≤ 30000 ) n (1≤n≤30000) n(1≤n≤30000),表示购来的纪念品的总件数。
第 3 3 3~ n + 2 n+2 n+2 行每行包含一个正整数 p i ( 5 ≤ p i ≤ w ) p_i (5≤p_i≤w) pi(5≤pi≤w),表示所对应纪念品的价格。
输出描述
输出一行,包含一个整数,即最少的分组数目。
w = int(input())
n = int(input())
a = []
for i in range(n):a.append(int(input()))a.sort()
l, r = 0, n - 1
ans = 0while True:if l == r:ans += 1breakif l > r:breakif a[l] + a[r] <= w:ans += 1l += 1r -= 1else:ans += 1r -= 1
print(ans)
翻硬币问题
题目描述
小明正在玩一个"翻硬币"的游戏。
桌上放着排成一排的若干硬币。我们用 ∗ * ∗ 表示正面,用 o o o 表示反面(是小写字母,不是零)。
比如,可能情形是: ∗ ∗ o o ∗ ∗ ∗ o o o o **oo***oooo ∗∗oo∗∗∗oooo;
如果同时翻转左边的两个硬币,则变为: o o o o ∗ ∗ ∗ o o o o oooo***oooo oooo∗∗∗oooo。
现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作。
输入描述
两行等长的字符串,分别表示初始状态和要达到的目标状态。
每行的长度<1000。
输出描述
一个整数,表示最小操作步数。
s = list(input())
t = list(input())
n = len(s)
ans = 0
for i in range(n):if s[i] == t[i]:continueif s[i + 1] == '*':s[i + 1] = 'o'else:s[i + 1] = '*'ans += 1
print(ans)
数组乘积问题
给定两个长度为 n n n 的正整数数组 a a a 和 b b b,可以任意排序,求 ∑ i = 1 n a [ i ] ∗ b [ i ] \sum_{i=1}^{n}a[i]*b[i] ∑i=1na[i]∗b[i] 的最小值
思路: a a a 从小到大, b b b 从大到小,然后对应元素相乘结果最小
参考个人博客:贪心
相关文章:

Python贪心
贪心 贪心:把整体问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直至所有步骤结束;每个步骤不会影响后续步骤核心性质:每次采用局部最优,最终结果就是全局最优如果题目满足上述核心性质…...

rk3568 内核态OOM内存泄漏kmemleak使用
1,配置,修改\kernel\arch\arm64\configs\rockchip_linux_defconfig,修改后查看.config. larkubuntu:~/Public/rk356x-linux/rk356x-linux/kernel$ cat .config | grep -i kmemleak CONFIG_HAVE_DEBUG_KMEMLEAKy CONFIG_DEBUG_KMEMLEAKy CONFI…...

ASP.NET Core - 日志记录系统(二)
ASP.NET Core - 日志记录系统(二) 2.4 日志提供程序2.4.1 内置日志提供程序2.4.2 源码解析 本篇接着上一篇 ASP.NET Core - 日志记录系统(一) 往下讲,所以目录不是从 1 开始的。 2.4 日志提供程序 2.4.1 内置日志提供程序 ASP.NET Core 包括…...

阿里云直播互动Web
官方文档:互动消息Web端集成方法_视频直播(LIVE)-阿里云帮助中心 以下是代码实现: <!-- 引入阿里云互动文件 --> <script src"https://g.alicdn.com/code/lib/jquery/3.7.1/jquery.min.js"></script> <script src&quo…...

解锁无证身份核验:开启便捷安全新征程
在当今快速发展的数字化时代,身份核验作为确保信息安全与交易诚信的基石,正经历着前所未有的变革。传统的身份核验方式,如携带身份证件进行现场验证,虽在一定程度上保障了安全,却也带来了诸多不便。随着科技的进步&…...

[DO374] Ansible 配置文件
[DO374] Ansible 配置文件 1. 配置文件位置2. 配置文件3. Ansible 配置4. Ansible的Ad-hoc5. Ansible 模块6. playbook段落7. 任务执行后续8. Ansible 变量8.1 ansible 变量的定义8.1.1 主机变量8.1.2 主机组变量 8.2 vars的循环 9. Ansible Collection10. Ansible-galaxy 安装…...

【杂谈】-50+个生成式人工智能面试问题(四)
7、生成式AI面试问题与微调相关 Q23. LLMs中的微调是什么? 答案:虽然预训练语言模型非常强大,但它们并不是任何特定任务的专家。它们可能对语言有惊人的理解能力,但仍需要一些LLMs微调过程,开发者通过这个过程提升它…...

RuoYi Cloud项目解读【四、项目配置与启动】
四、项目配置与启动 当上面环境全部准备好之后,接下来就是项目配置。需要将项目相关配置修改成当前相关环境。 1 后端配置 1.1 数据库 创建数据库ry-cloud并导入数据脚本ry_2024xxxx.sql(必须),quartz.sql(可选&…...

51c~Pytorch~合集5
我自己的原文哦~ https://blog.51cto.com/whaosoft/13059544 一、PyTorch DDP 正在郁闷呢 jetson nx 的torchvision安装~~ 自带就剩5g 想弄到ssd 项目中的 venv中又 cuda.h没有... 明明已经装好什么都对 算了说今天主题 啊对 还是搬运啊 学习之工具人而已 勿怪 Distrib…...

【芯片封测学习专栏 -- 什么是 Chiplet 技术】
请阅读【嵌入式开发学习必备专栏 Cache | MMU | AMBA BUS | CoreSight | Trace32 | CoreLink | ARM GCC | CSH】 文章目录 OverviewChiplet 背景UCIeChiplet 的挑战 Overview Chiplet 又称为小芯片。该技术通过将大型SoC划分为更小的芯片,使得每个部分都能采用不同…...
)
Java SpringBoot + Vue + Uniapp 集成JustAuth 最快实现多端三方登录!(QQ登录、微信登录、支付宝登录……)
注:本文基于 若依 集成just-auth实现第三方授权登录 修改完善,所有步骤仅代表本人如下环境亲测可用,其他环境需自辩或联系查看原因! 系统环境 运行系统:Windows10专业版、Linux Centos7.6 Java 版本:1.8.0_…...

支持向量回归(SVR:Support Vector Regression)用于A股数据分析、预测
简单说明 支持向量回归是一种用来做预测的数学方法,属于「机器学习」的一种。 它的目标是找到一条「最合适的线」,能够大致描述数据点的趋势,并允许数据点离这条线有一定的误差(不要求所有点都完全落在这条线上)。 可以把它想象成:找到一条「宽带」或「隧道」,大部分…...

ZYNQ初识10(zynq_7010)UART通信实验
基于bi站正点原子讲解视频: 系统框图(基于串口的数据回环)如下: 以下,是串口接收端的波形图,系统时钟和波特率时钟不同,为异步时钟,,需要先延时两拍,将时钟同…...

专题 - STM32
基础 基础知识 STM所有产品线(列举型号): STM产品的3内核架构(列举ARM芯片架构): STM32的3开发方式: STM32的5开发工具和套件: 若要在电脑上直接硬件级调试STM32设备,则…...

2 XDMA IP中断
三种中断 1. Legacy 定义:Legacy 中断是传统的中断处理方式,使用物理中断线(例如 IRQ)来传递中断信号。缺点: 中断线数量有限,通常为 16 条,限制了可连接设备的数量。中断处理可能会导致中断风…...
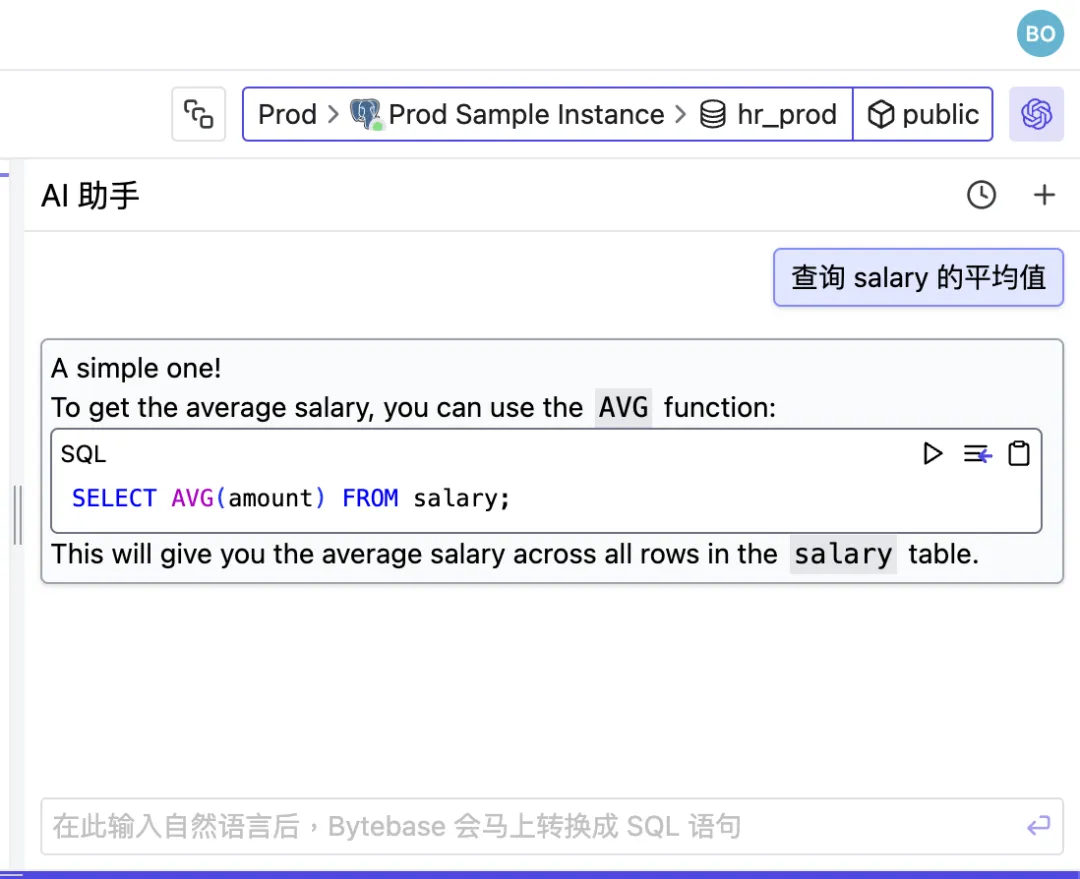
自然语言转 SQL:通过 One API 将 llama3 模型部署在 Bytebase SQL 编辑器
使用 Open AI 兼容的 API,可以在 Bytebase SQL 编辑器中使用自然语言查询数据库。 出于数据安全的考虑,私有部署大语言模型是一个较好的选择 – 本文选择功能强大的开源模型 llama3。 由于 OpenAI 默认阻止出站流量,为了简化网络配置&#…...

抖音矩阵是什么
抖音矩阵是指在同一品牌或个人IP下,通过创建多个不同定位的抖音账号(如主号、副号、子号等),形成一个有机的整体,以实现多维度、多层次的内容覆盖和用户互动。以下是关于抖音矩阵的详细介绍: 抖音矩阵的类…...

怎么抓取ios 移动app的https请求?
怎么抓取IOS应用程序里面的https? 这个涉及到2个问题 1.电脑怎么抓到IOS手机流量? 2.HTTPS怎么解密? 部分app可以使用代理抓包的方式,但是正式点的app用代理抓包是抓不到的,例如pin检测,证书双向校验等…...

pyqt鸟瞰
QApplication是Qt框架中的一个类,专门用于管理基于QWidget的图形用户界面(GUI)应用程序的控制流和主要设置。QApplication类继承自QGuiApplication,提供了许多与GUI相关的功能,如窗口系统集成、事件处理等。 QAppli…...
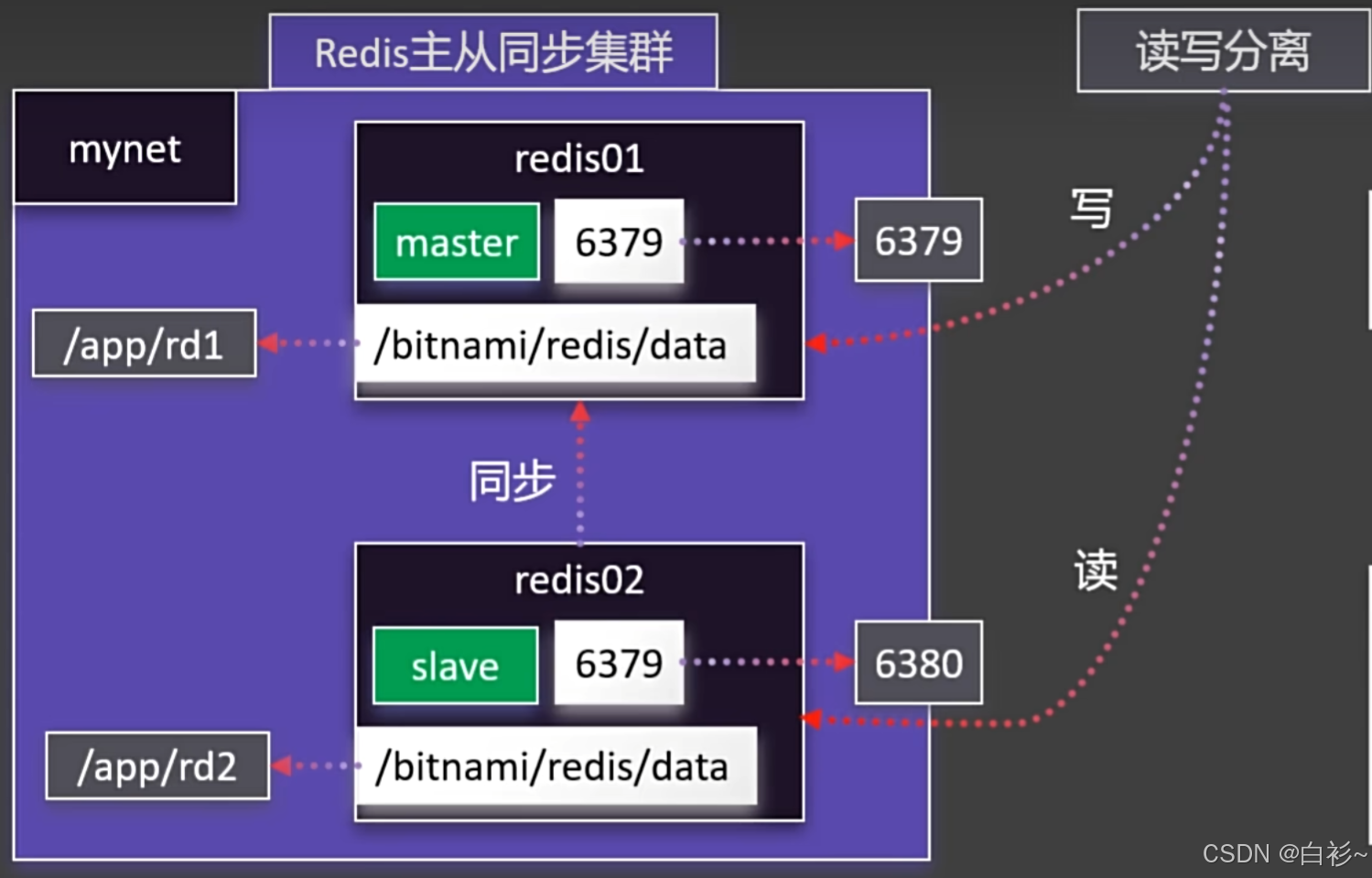
【Docker】入门教程
目录 一、Docker的安装 二、Docker的命令 Docker命令实验 1.下载镜像 2.启动容器 3.修改页面 4.保存镜像 5.分享社区 三、Docker存储 1.目录挂载 2.卷映射 四、Docker网络 1.容器间相互访问 2.Redis主从同步集群 3.启动MySQL 五、Docker Compose 1.命令式安装 …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
