题解:P10972 I-Country
题目传送门
思路
因为占据的连通块的左端点先递减、后递增,右端点先递增、后递减,所以设 f i , j , l , r , x ( 0 / 1 ) , y ( 0 / 1 ) f_{i,j,l,r,x(0/1),y(0/1)} fi,j,l,r,x(0/1),y(0/1) 为前 i i i 行中,选择 j j j 个方格,其中第 i i i 行选择的区间的左端点为 l l l,右端点为 r r r, x x x 表示左端点是否出现递增, y y y 表示右端点是否递增的所有方案的最大石油数量。
容易列出状态转移方程,
f i , j , l , r , 0 , 0 = max { f i − 1 , j − ( r − l + 1 ) , a , b , 0 , 0 , f i − 1 , j − ( r − l + 1 ) , a , b , 0 , 1 } + s i , r − s i , l − 1 f i , j , l , r , 0 , 1 = max { f i − 1 , j − ( r − l + 1 ) , a , b , 0 , 1 } + s i , r − s i , l − 1 f i , j , l , r , 1 , 0 = max { f i − 1 , j − ( r − l + 1 ) , a , b , 0 , 0 , f i − 1 , j − ( r − l + 1 ) , a , b , 0 , 1 , f i − 1 , j − ( r − l + 1 ) , a , b , 1 , 0 , f i − 1 , j − ( r − l + 1 ) , a , b , 1 , 1 } + s i , r − s i , l − 1 f i , j , l , r , 1 , 1 = max { f i − 1 , j − ( r − l + 1 ) , a , b , 0 , 1 , f i − 1 , j − ( r − l + 1 ) , a , b , 1 , 1 } + s i , r − s i , l − 1 f_{i,j,l,r,0,0}=\max\{f_{i-1,j-(r-l+1),a,b,0,0},f_{i-1,j-(r-l+1),a,b,0,1}\}+s_{i,r}-s_{i,l-1}\\ f_{i,j,l,r,0,1}=\max\{f_{i-1,j-(r-l+1),a,b,0,1}\}+s_{i,r}-s_{i,l-1}\\ f_{i,j,l,r,1,0}=\max\{f_{i-1,j-(r-l+1),a,b,0,0},f_{i-1,j-(r-l+1),a,b,0,1},f_{i-1,j-(r-l+1),a,b,1,0},f_{i-1,j-(r-l+1),a,b,1,1}\}+s_{i,r}-s_{i,l-1}\\ f_{i,j,l,r,1,1}=\max\{f_{i-1,j-(r-l+1),a,b,0,1},f_{i-1,j-(r-l+1),a,b,1,1}\}+s_{i,r}-s_{i,l-1}\\ fi,j,l,r,0,0=max{fi−1,j−(r−l+1),a,b,0,0,fi−1,j−(r−l+1),a,b,0,1}+si,r−si,l−1fi,j,l,r,0,1=max{fi−1,j−(r−l+1),a,b,0,1}+si,r−si,l−1fi,j,l,r,1,0=max{fi−1,j−(r−l+1),a,b,0,0,fi−1,j−(r−l+1),a,b,0,1,fi−1,j−(r−l+1),a,b,1,0,fi−1,j−(r−l+1),a,b,1,1}+si,r−si,l−1fi,j,l,r,1,1=max{fi−1,j−(r−l+1),a,b,0,1,fi−1,j−(r−l+1),a,b,1,1}+si,r−si,l−1
。
注意,由于联通,所以 r ≥ a r\ge a r≥a 且 l ≤ b l\le b l≤b。因为递增递减,所以当 x = 0 x=0 x=0 时, l ≤ a l\le a l≤a,当 x = 1 x=1 x=1 时, l ≥ a l\ge a l≥a,当 y = 0 y=0 y=0 时, r ≤ b r\le b r≤b,当 y = 1 y=1 y=1 时, r ≥ b r\ge b r≥b。 s i , j s_{i,j} si,j 为第 i i i 行的前缀和,不是二维前缀和。
最终答案为 max { f i , k , l , r , x , y } \max\{f_{i,k,l,r,x,y}\} max{fi,k,l,r,x,y},输出路径可以存一个结构体 l a i , j , l , r , x , y la_{i,j,l,r,x,y} lai,j,l,r,x,y 统计 f i , j , l , r , x , y f_{i,j,l,r,x,y} fi,j,l,r,x,y 从哪里转移来。
思路容易想,代码细节却很多,本人被硬控了几个小时。
代码
//要C++14(GCC 9),不然会RE
#include <bits/stdc++.h>
using namespace std;
const int N=25;
struct Last{int i,j,l,r,x,y;
}la[N][N*N][N][N][2][2];
int n,m,k,a[N][N],s[N][N],f[N][N*N][N][N][2][2];
int main(){scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);s[i][j]=s[i][j-1]+a[i][j];}for(int i=1;i<=n;i++)for(int j=1;j<=i*m;j++)for(int l=1;l<=m;l++)for(int r=l;r<=m;r++){if(r-l+1+(i-1)*m<j || j<r-l+1)continue;int sum=s[i][r]-s[i][l-1];if(i==1){f[i][j][l][r][0][0]=f[i][j][l][r][0][1]=f[i][j][l][r][1][0]=f[i][j][l][r][1][1]=sum;continue;}//x=0,y=0for(int x=1;x<=m;x++)for(int y=x;y<=m;y++)if(!(y<l || x>r) && x>=l && y>=r){//注意要联通,l要递减,r要递减if(f[i-1][j-(r-l+1)][x][y][0][0]+sum>f[i][j][l][r][0][0])f[i][j][l][r][0][0]=f[i-1][j-(r-l+1)][x][y][0][0]+sum,la[i][j][l][r][0][0]={i-1,j-(r-l+1),x,y,0,0};if(f[i-1][j-(r-l+1)][x][y][0][1]+sum>f[i][j][l][r][0][0])f[i][j][l][r][0][0]=f[i-1][j-(r-l+1)][x][y][0][1]+sum,la[i][j][l][r][0][0]={i-1,j-(r-l+1),x,y,0,1};}//x=0,y=1for(int x=1;x<=m;x++)for(int y=x;y<=m;y++)if(!(y<l || x>r) && x>=l && y<=r){//l要递减,r要递增if(f[i-1][j-(r-l+1)][x][y][0][1]+sum>f[i][j][l][r][0][1])f[i][j][l][r][0][1]=f[i-1][j-(r-l+1)][x][y][0][1]+sum,la[i][j][l][r][0][1]={i-1,j-(r-l+1),x,y,0,1};}//x=1,y=0for(int x=1;x<=m;x++)for(int y=x;y<=m;y++)if(!(y<l || x>r) && x<=l && y>=r){//l要递增,r要递减if(f[i-1][j-(r-l+1)][x][y][0][0]+sum>f[i][j][l][r][1][0])f[i][j][l][r][1][0]=f[i-1][j-(r-l+1)][x][y][0][0]+sum,la[i][j][l][r][1][0]={i-1,j-(r-l+1),x,y,0,0};if(f[i-1][j-(r-l+1)][x][y][0][1]+sum>f[i][j][l][r][1][0])f[i][j][l][r][1][0]=f[i-1][j-(r-l+1)][x][y][0][1]+sum,la[i][j][l][r][1][0]={i-1,j-(r-l+1),x,y,0,1};if(f[i-1][j-(r-l+1)][x][y][1][0]+sum>f[i][j][l][r][1][0])f[i][j][l][r][1][0]=f[i-1][j-(r-l+1)][x][y][1][0]+sum,la[i][j][l][r][1][0]={i-1,j-(r-l+1),x,y,1,0};if(f[i-1][j-(r-l+1)][x][y][1][1]+sum>f[i][j][l][r][1][0])f[i][j][l][r][1][0]=f[i-1][j-(r-l+1)][x][y][1][1]+sum,la[i][j][l][r][1][0]={i-1,j-(r-l+1),x,y,1,1};}//x=1,y=1for(int x=1;x<=m;x++)for(int y=x;y<=m;y++)if(!(y<l || x>r) && x<=l && y<=r){//l要递增,r要递增if(f[i-1][j-(r-l+1)][x][y][0][1]+sum>f[i][j][l][r][1][1])f[i][j][l][r][1][1]=f[i-1][j-(r-l+1)][x][y][0][1]+sum,la[i][j][l][r][1][1]={i-1,j-(r-l+1),x,y,0,1};if(f[i-1][j-(r-l+1)][x][y][1][1]+sum>f[i][j][l][r][1][1])f[i][j][l][r][1][1]=f[i-1][j-(r-l+1)][x][y][1][1]+sum,la[i][j][l][r][1][1]={i-1,j-(r-l+1),x,y,1,1};}}int ans=0;Last tmp;for(int i=1;i<=n;i++)for(int l=1;l<=m;l++)for(int r=l;r<=m;r++){if(f[i][k][l][r][0][0]>ans)ans=f[i][k][l][r][0][0],tmp={i,k,l,r,0,0};//tmp存储当前的状态if(f[i][k][l][r][0][1]>ans)ans=f[i][k][l][r][0][1],tmp={i,k,l,r,0,1};if(f[i][k][l][r][1][0]>ans)ans=f[i][k][l][r][1][0],tmp={i,k,l,r,1,0};if(f[i][k][l][r][1][1]>ans)ans=f[i][k][l][r][1][1],tmp={i,k,l,r,1,1};}printf("Oil : %d",ans);while(tmp.j && tmp.i){//输出路径for(int i=tmp.l;i<=tmp.r;i++)printf("\n%d %d",tmp.i,i);tmp=la[tmp.i][tmp.j][tmp.l][tmp.r][tmp.x][tmp.y];}return 0;
}
相关文章:

题解:P10972 I-Country
题目传送门 思路 因为占据的连通块的左端点先递减、后递增,右端点先递增、后递减,所以设 f i , j , l , r , x ( 0 / 1 ) , y ( 0 / 1 ) f_{i,j,l,r,x(0/1),y(0/1)} fi,j,l,r,x(0/1),y(0/1) 为前 i i i 行中,选择 j j j 个方格&#x…...

linux常用加固方式
目录 一.系统加固 二.ssh加固 三.换个隐蔽的端口 四.防火墙配置 五.用户权限管理 六.暴力破解防护 七.病毒防护 八.磁盘加密 九.双因素认证2FA 十.日志监控 十一.精简服务 一.系统加固 第一步:打好系统补丁 sudo apt update && sudo apt upgra…...
:自然语言处理)
笔灵ai写作技术浅析(二):自然语言处理
一、词法分析(Lexical Analysis) 1.1 概述 词法分析是NLP的第一步,主要任务是将连续的文本分割成有意义的单元(词或词组),并对这些单元进行标注,如词性标注(POS tagging)。词法分析的质量直接影响后续的句法分析和语义理解。 1.2 技术细节 1.分词(Tokenization)…...

PyCharm介绍
PyCharm的官网是https://www.jetbrains.com/pycharm/。 以下是在PyCharm官网下载和安装软件的步骤: 下载步骤 打开浏览器,访问PyCharm的官网https://www.jetbrains.com/pycharm/。在官网首页,点击“Download”按钮进入下载页面。选择适合自…...

深度解析:基于Vue 3与Element Plus的学校管理系统技术实现
一、项目架构分析 1.1 技术栈全景 核心框架:Vue 3 TypeScript UI组件库:Element Plus(含图标动态注册) 状态管理:Pinia(用户状态持久化) 路由方案:Vue Router(动态路…...

Python从0到100(八十五):神经网络-使用迁移学习完成猫狗分类
前言: 零基础学Python:Python从0到100最新最全教程。 想做这件事情很久了,这次我更新了自己所写过的所有博客,汇集成了Python从0到100,共一百节课,帮助大家一个月时间里从零基础到学习Python基础语法、Python爬虫、Web开发、 计算机视觉、机器学习、神经网络以及人工智能…...

苍穹外卖 项目记录 day09 历史订单
文章目录 查询历史订单查询订单详情取消订单再来一单 查询历史订单 分页查询历史订单可以根据订单状态查询展示订单数据时,需要展示的数据包括:下单时间、订单状态、订单金额、订单明细(商品名称、图片) #OrderController/*** 历…...

记录 | 基于Docker Desktop的MaxKB安装
目录 前言一、MaxKBStep 1Step2 二、运行MaxKB更新时间 前言 参考文章:如何利用智谱全模态免费模型,生成大家都喜欢的图、文、视并茂的文章! MaxKB的Github下载地址 参考视频:【2025最新MaxKB教程】10分钟学会一键部署本地私人专属…...
)
WordPress web-directory-free插件存在本地文件包含导致任意文件读取漏洞(CVE-2024-3673)
免责声明: 本文旨在提供有关特定漏洞的深入信息,帮助用户充分了解潜在的安全风险。发布此信息的目的在于提升网络安全意识和推动技术进步,未经授权访问系统、网络或应用程序,可能会导致法律责任或严重后果。因此,作者不对读者基于本文内容所采取的任何行为承担责任。读者在…...

LLM:BERT or BART 之BERT
文章目录 前言一、BERT1. Decoder-only2. Encoder-only3. Use of Bidirectional Context4. Masked Language Model (MLM)5. Next Sentence Prediction (NSP)6. Fine-tune1、情感分析2、句对分析3、命名实体识别(NER) 7. BERT总结 总结 前言 NLP选手对这…...

EtherCAT主站IGH-- 18 -- IGH之fsm_mbox_gateway.h/c文件解析
EtherCAT主站IGH-- 18 -- IGH之fsm_mbox_gateway.h/c文件解析 0 预览一 该文件功能`fsm_mbox_gateway.c` 文件功能函数预览二 函数功能介绍`fsm_mbox_gateway.c` 中主要函数的作用1. `ec_fsm_mbg_init`2. `ec_fsm_mbg_clear`3. `ec_fsm_mbg_transfer`4. `ec_fsm_mbg_exec`5. `e…...

深入探讨防抖函数中的 this 上下文
深入剖析防抖函数中的 this 上下文 最近我在研究防抖函数实现的时候,发现一个耗费脑子的问题,出现了令我困惑的问题。接下来,我将通过代码示例,深入探究这些现象背后的原理。 示例代码 function debounce(fn, delay) {let time…...

【AI论文】魔鬼在细节:关于在训练专用混合专家模型时实现负载均衡损失
摘要:本文重新审视了在训练混合专家(Mixture-of-Experts, MoEs)模型时负载均衡损失(Load-Balancing Loss, LBL)的实现。具体来说,MoEs的LBL定义为N_E乘以从1到N_E的所有专家i的频率f_i与门控得分平均值p_i的…...

Gurobi基础语法之addVar 和 addVars
addVar 和 addVars作为 Gurobi模型对象中的方法,常常用来生成变量,本文介绍了Python中的这两个接口的使用 addVar addVar(lb0.0, ubfloat(inf), obj0.0, vtypeGRB.CONTINUOUS, name, columnNone) lb 和 ub让变量在生成的时候就有下界和上届,…...
---函数)
C语言学习阶段性总结(五)---函数
函数构成五要素: 1、返回值类型 2、函数名 3、参数列表(输入) 4、函数体 (算法) 5、返回值 (输出) 返回值类型 函数名 (参数列表) { 函数体; return 返回值; } void 类型…...

K8S 快速实战
K8S 核心架构原理: 我们已经知道了 K8S 的核心功能:自动化运维管理多个容器化程序。那么 K8S 怎么做到的呢?这里,我们从宏观架构上来学习 K8S 的设计思想。首先看下图: K8S 是属于主从设备模型(Master-Slave 架构),即有 Master 节点负责核心的调度、管理和运维,Slave…...

java后端之事务管理
Transactional注解:作用于业务层的方法、类、接口上,将当前方法交给spring进行事务管理,执行前开启事务,成功执行则提交事务,执行异常回滚事务 spring事务管理日志: 默认情况下,只有出现Runti…...

【Redis】缓存+分布式锁
目录 缓存 Redis最主要的使用场景就是作为缓存 缓存的更新策略: 1.定期生成 2.实时生成 面试重点: 缓存预热(Cache preheating): 缓存穿透(Cache penetration) 缓存雪崩 (Cache avalan…...

二分查找题目:寻找两个正序数组的中位数
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:寻找两个正序数组的中位数 出处:4. 寻找两个正序数组的中位数 难度 8 级 题目描述 要求 给定两个大…...
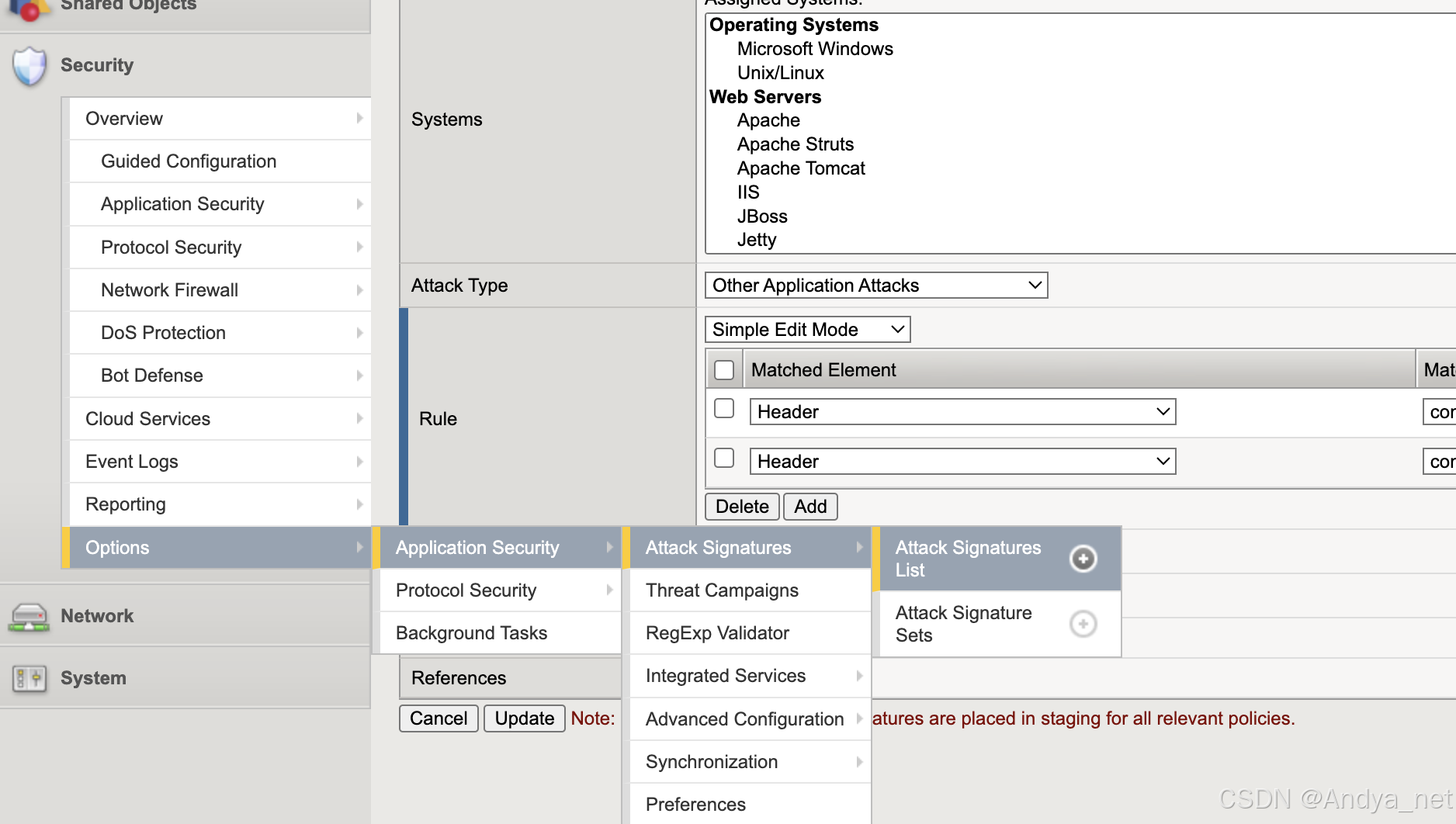
网络安全 | F5-Attack Signatures详解
关注:CodingTechWork 关于攻击签名 攻击签名是用于识别 Web 应用程序及其组件上攻击或攻击类型的规则或模式。安全策略将攻击签名中的模式与请求和响应的内容进行比较,以查找潜在的攻击。有些签名旨在保护特定的操作系统、Web 服务器、数据库、框架或应…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...

21-Oracle 23 ai-Automatic SQL Plan Management(SPM)
小伙伴们,有没有迁移数据库完毕后或是突然某一天在同一个实例上同样的SQL, 性能不一样了、业务反馈卡顿、业务超时等各种匪夷所思的现状。 于是SPM定位开始,OCM考试中SPM必考。 其他的AWR、ASH、SQLHC、SQLT、SQL profile等换作下一个话题…...

简单聊下阿里云DNS劫持事件
阿里云域名被DNS劫持事件 事件总结 根据ICANN规则,域名注册商(Verisign)认定aliyuncs.com域名下的部分网站被用于非法活动(如传播恶意软件);顶级域名DNS服务器将aliyuncs.com域名的DNS记录统一解析到shado…...
