二分查找题目:寻找两个正序数组的中位数
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:寻找两个正序数组的中位数
出处:4. 寻找两个正序数组的中位数
难度
8 级
题目描述
要求
给定两个大小分别为 m \texttt{m} m 和 n \texttt{n} n 的升序数组 nums1 \texttt{nums1} nums1 和 nums2 \texttt{nums2} nums2,返回这两个升序数组的中位数。
要求时间复杂度是 O(log (m + n)) \texttt{O(log (m + n))} O(log (m + n))。
示例
示例 1:
输入: nums1 = [1,3], nums2 = [2] \texttt{nums1 = [1,3], nums2 = [2]} nums1 = [1,3], nums2 = [2]
输出: 2.00000 \texttt{2.00000} 2.00000
解释:合并数组是 [1,2,3] \texttt{[1,2,3]} [1,2,3],中位数是 2 \texttt{2} 2。
示例 2:
输入: nums1 = [1,2], nums2 = [3,4] \texttt{nums1 = [1,2], nums2 = [3,4]} nums1 = [1,2], nums2 = [3,4]
输出: 2.50000 \texttt{2.50000} 2.50000
解释:合并数组是 [1,2,3,4] \texttt{[1,2,3,4]} [1,2,3,4],中位数是 2 + 3 2 = 2.5 \dfrac{\texttt{2} + \texttt{3}}{\texttt{2}} = \texttt{2.5} 22+3=2.5。
数据范围
- nums1.length = m \texttt{nums1.length} = \texttt{m} nums1.length=m
- nums2.length = n \texttt{nums2.length} = \texttt{n} nums2.length=n
- 0 ≤ m ≤ 1000 \texttt{0} \le \texttt{m} \le \texttt{1000} 0≤m≤1000
- 0 ≤ n ≤ 1000 \texttt{0} \le \texttt{n} \le \texttt{1000} 0≤n≤1000
- 1 ≤ m + n ≤ 2000 \texttt{1} \le \texttt{m} + \texttt{n} \le \texttt{2000} 1≤m+n≤2000
- -10 6 ≤ nums1[i], nums2[i] ≤ 10 6 \texttt{-10}^\texttt{6} \le \texttt{nums1[i], nums2[i]} \le \texttt{10}^\texttt{6} -106≤nums1[i], nums2[i]≤106
解法一
思路和算法
已知两个升序数组的长度分别是 m m m 和 n n n。计算两个升序数组的中位数可以转换成找到两个升序数组的所有元素中的第 k k k 小元素,其中 0 ≤ k < m + n 0 \le k < m + n 0≤k<m+n。用 total = m + n \textit{total} = m + n total=m+n 表示两个升序数组的长度之和。当 total \textit{total} total 是奇数时, k = total − 1 2 k = \dfrac{\textit{total} - 1}{2} k=2total−1,第 k k k 小元素即为中位数;当 total \textit{total} total 是偶数时,分别取 k = total 2 − 1 k = \dfrac{\textit{total}}{2} - 1 k=2total−1 和 k = total 2 k = \dfrac{\textit{total}}{2} k=2total,两次第 k k k 小元素的平均数即为中位数。因此,根据两个升序数组的长度之和是奇数或偶数,执行一次或两次寻找第 k k k 小元素的操作,即可得到中位数。
由于题目要求时间复杂度是 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n)),因此要求每次寻找第 k k k 小元素的操作的时间复杂度是 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n))。需要使用二分查找实现。
用 k k k 表示目标值在剩余元素中的序号( k k k 从 0 0 0 开始,序号为 k k k 表示剩余元素中有 k k k 个元素小于等于目标值),用 index 1 \textit{index}_1 index1 和 index 2 \textit{index}_2 index2 分别表示数组 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 的首个剩余元素的下标,初始时 index 1 \textit{index}_1 index1 和 index 2 \textit{index}_2 index2 都等于 0 0 0。剩余元素表示可能是目标值的元素,查找过程中将不可能是目标值的元素排除。
每次查找时,分别考虑两个数组的剩余元素中最小的 ⌈ k 2 ⌉ \Big\lceil \dfrac{k}{2} \Big\rceil ⌈2k⌉ 个元素,共考虑 k + 1 k + 1 k+1 个元素(当 k k k 是奇数时)或 k k k 个元素(当 k k k 是偶数时),这些元素在两个数组中的下标范围分别是 nums 1 \textit{nums}_1 nums1 的下标范围 [ index 1 , endIndex 1 ] [\textit{index}_1, \textit{endIndex}_1] [index1,endIndex1] 和 nums 2 \textit{nums}_2 nums2 的下标范围 [ index 2 , endIndex 2 ] [\textit{index}_2, \textit{endIndex}_2] [index2,endIndex2],其中 endIndex 1 = index 1 + ⌊ k − 1 2 ⌋ \textit{endIndex}_1 = \textit{index}_1 + \Big\lfloor \dfrac{k - 1}{2} \Big\rfloor endIndex1=index1+⌊2k−1⌋, endIndex 2 = index 2 + ⌊ k − 1 2 ⌋ \textit{endIndex}_2 = \textit{index}_2 + \Big\lfloor \dfrac{k - 1}{2} \Big\rfloor endIndex2=index2+⌊2k−1⌋。考虑 nums 1 [ endIndex 1 ] \textit{nums}_1[\textit{endIndex}_1] nums1[endIndex1] 和 nums 2 [ endIndex 2 ] \textit{nums}_2[\textit{endIndex}_2] nums2[endIndex2],其中的较大值是第 k k k 小元素(当 k k k 是奇数时)或第 k − 1 k - 1 k−1 小元素(当 k k k 是偶数时),因此其中的较小值一定不是第 k k k 小元素。对于较小值所在的数组,可以将较小值以及较小值前面的元素全部排除。
需要注意的是, endIndex 1 \textit{endIndex}_1 endIndex1 和 endIndex 2 \textit{endIndex}_2 endIndex2 不能超出数组下标范围。如果一个数组的剩余元素个数少于 ⌈ k 2 ⌉ \Big\lceil \dfrac{k}{2} \Big\rceil ⌈2k⌉,则该数组中考虑的元素是该数组中的全部剩余元素。因此有 endIndex 1 = min ( index 1 + ⌊ k − 1 2 ⌋ , m − 1 ) \textit{endIndex}_1 = \min(\textit{index}_1 + \Big\lfloor \dfrac{k - 1}{2} \Big\rfloor, m - 1) endIndex1=min(index1+⌊2k−1⌋,m−1), endIndex 2 = min ( index 2 + ⌊ k − 1 2 ⌋ , n − 1 ) \textit{endIndex}_2 = \min(\textit{index}_2 + \Big\lfloor \dfrac{k - 1}{2} \Big\rfloor, n - 1) endIndex2=min(index2+⌊2k−1⌋,n−1)。
由此可以根据三种情况分别做相应的处理,缩小查找范围。
-
如果 nums 1 [ endIndex 1 ] < nums 2 [ endIndex 2 ] \textit{nums}_1[\textit{endIndex}_1] < \textit{nums}_2[\textit{endIndex}_2] nums1[endIndex1]<nums2[endIndex2],则将 nums 1 \textit{nums}_1 nums1 的下标范围 [ index 1 , endIndex 1 ] [\textit{index}_1, \textit{endIndex}_1] [index1,endIndex1] 中的元素全部排除,排除的元素个数是 endIndex 1 − index 1 + 1 \textit{endIndex}_1 - \textit{index}_1 + 1 endIndex1−index1+1。
-
如果 nums 1 [ endIndex 1 ] > nums 2 [ endIndex 2 ] \textit{nums}_1[\textit{endIndex}_1] > \textit{nums}_2[\textit{endIndex}_2] nums1[endIndex1]>nums2[endIndex2],则将 nums 2 \textit{nums}_2 nums2 的下标范围 [ index 2 , endIndex 2 ] [\textit{index}_2, \textit{endIndex}_2] [index2,endIndex2] 中的元素全部排除,排除的元素个数是 endIndex 2 − index 2 + 1 \textit{endIndex}_2 - \textit{index}_2 + 1 endIndex2−index2+1。
-
如果 nums 1 [ endIndex 1 ] = nums 2 [ endIndex 2 ] \textit{nums}_1[\textit{endIndex}_1] = \textit{nums}_2[\textit{endIndex}_2] nums1[endIndex1]=nums2[endIndex2],则处理方式和 nums 1 [ endIndex 1 ] < nums 2 [ endIndex 2 ] \textit{nums}_1[\textit{endIndex}_1] < \textit{nums}_2[\textit{endIndex}_2] nums1[endIndex1]<nums2[endIndex2] 相同。
每次查找之后,将 k k k 的值减去排除的元素个数,并将排除元素的数组的相应下标更新为该数组首个剩余元素的下标,具体做法如下:如果排除的是 nums 1 \textit{nums}_1 nums1 中的元素,则将 index 1 \textit{index}_1 index1 更新为 endIndex 1 + 1 \textit{endIndex}_1 + 1 endIndex1+1;如果排除的是 nums 2 \textit{nums}_2 nums2 中的元素,则将 index 2 \textit{index}_2 index2 更新为 endIndex 2 + 1 \textit{endIndex}_2 + 1 endIndex2+1。
二分查找的条件是 index 1 < m \textit{index}_1 < m index1<m, index 2 < n \textit{index}_2 < n index2<n 和 k > 0 k > 0 k>0。如果三个条件之一不满足,则二分查找结束,得到目标值。
-
如果 index 1 = m \textit{index}_1 = m index1=m,则剩余元素都在 nums 2 \textit{nums}_2 nums2 中,目标值是 nums 2 [ index 2 + k ] \textit{nums}_2[\textit{index}_2 + k] nums2[index2+k]。
-
如果 index 2 = n \textit{index}_2 = n index2=n,则剩余元素都在 nums 1 \textit{nums}_1 nums1 中,目标值是 nums 1 [ index 1 + k ] \textit{nums}_1[\textit{index}_1 + k] nums1[index1+k]。
-
如果 k = 0 k = 0 k=0,则剩余元素中的最小元素是目标值,目标值是 min ( nums 1 [ index 1 ] , nums 2 [ index 2 ] ) \min(\textit{nums}_1[\textit{index}_1], \textit{nums}_2[\textit{index}_2]) min(nums1[index1],nums2[index2])。
以下用一个例子说明该解法。
两个数组是 nums 1 = [ 1 , 2 , 3 , 4 , 5 ] \textit{nums}_1 = [1, 2, 3, 4, 5] nums1=[1,2,3,4,5], nums 2 = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] \textit{nums}_2 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] nums2=[1,2,3,4,5,6,7,8,9,10],两个数组的长度分别是 m = 5 m = 5 m=5, n = 10 n = 10 n=10,长度之和是 15 15 15, k = 7 k = 7 k=7。初始时, index 1 = 0 \textit{index}_1 = 0 index1=0, index 2 = 0 \textit{index}_2 = 0 index2=0。
-
根据 index 1 = 0 \textit{index}_1 = 0 index1=0, index 2 = 0 \textit{index}_2 = 0 index2=0 和 k = 7 k = 7 k=7 计算得到 endIndex 1 = 3 \textit{endIndex}_1 = 3 endIndex1=3, endIndex 2 = 3 \textit{endIndex}_2 = 3 endIndex2=3。由于 nums 1 [ 3 ] = nums 2 [ 3 ] \textit{nums}_1[3] = \textit{nums}_2[3] nums1[3]=nums2[3],因此将 nums 1 \textit{nums}_1 nums1 的下标范围 [ 0 , 3 ] [0, 3] [0,3] 排除,排除 4 4 4 个元素,更新得到 k = 3 k = 3 k=3, index 1 = 4 \textit{index}_1 = 4 index1=4。
-
根据 index 1 = 4 \textit{index}_1 = 4 index1=4, index 2 = 0 \textit{index}_2 = 0 index2=0 和 k = 3 k = 3 k=3 计算得到 endIndex 1 = 4 \textit{endIndex}_1 = 4 endIndex1=4, endIndex 2 = 1 \textit{endIndex}_2 = 1 endIndex2=1。由于 nums 1 [ 4 ] > nums 2 [ 1 ] \textit{nums}_1[4] > \textit{nums}_2[1] nums1[4]>nums2[1],因此将 nums 2 \textit{nums}_2 nums2 的下标范围 [ 0 , 1 ] [0, 1] [0,1] 排除,排除 2 2 2 个元素,更新得到 k = 1 k = 1 k=1, index 2 = 2 \textit{index}_2 = 2 index2=2。
-
根据 index 1 = 4 \textit{index}_1 = 4 index1=4, index 2 = 2 \textit{index}_2 = 2 index2=2 和 k = 1 k = 1 k=1 计算得到 endIndex 1 = 4 \textit{endIndex}_1 = 4 endIndex1=4, endIndex 2 = 2 \textit{endIndex}_2 = 2 endIndex2=2。由于 nums 1 [ 4 ] > nums 2 [ 2 ] \textit{nums}_1[4] > \textit{nums}_2[2] nums1[4]>nums2[2],因此将 nums 2 \textit{nums}_2 nums2 的下标范围 [ 2 , 2 ] [2, 2] [2,2] 排除,排除 1 1 1 个元素,更新得到 k = 0 k = 0 k=0, index 2 = 3 \textit{index}_2 = 3 index2=3。
-
此时 k = 0 k = 0 k=0,二分查找结束, nums 1 [ 4 ] \textit{nums}_1[4] nums1[4] 和 nums 2 [ 3 ] \textit{nums}_2[3] nums2[3] 中的较小值 4 4 4 即为目标值。
代码
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {int m = nums1.length, n = nums2.length;int total = m + n;if (total % 2 == 1) {int medianIndex = (total - 1) / 2;return findKthSmallest(medianIndex, nums1, nums2);} else {int medianIndex1 = total / 2 - 1, medianIndex2 = total / 2;return (findKthSmallest(medianIndex1, nums1, nums2) + findKthSmallest(medianIndex2, nums1, nums2)) / 2.0;}}public int findKthSmallest(int k, int[] nums1, int[] nums2) {int m = nums1.length, n = nums2.length;int index1 = 0, index2 = 0;while (index1 < m && index2 < n && k > 0) {int endIndex1 = Math.min(index1 + (k - 1) / 2, m - 1);int endIndex2 = Math.min(index2 + (k - 1) / 2, n - 1);int num1 = nums1[endIndex1], num2 = nums2[endIndex2];if (num1 <= num2) {k -= endIndex1 - index1 + 1;index1 = endIndex1 + 1;} else {k -= endIndex2 - index2 + 1;index2 = endIndex2 + 1;}}if (index1 == m) {return nums2[index2 + k];} else if (index2 == n) {return nums1[index1 + k];} else {return Math.min(nums1[index1], nums2[index2]);}}
}
复杂度分析
-
时间复杂度: O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n)),其中 m m m 和 n n n 分别是数组 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 的长度。每次寻找第 k k k 小元素时, k k k 的初始值是 m + n m + n m+n 的一半附近的整数,每次查找将 k k k 的值减小一半,因此时间复杂度是 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n))。
-
空间复杂度: O ( 1 ) O(1) O(1)。
解法二
思路和算法
解法一的时间复杂度是 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n)),该时间复杂度已经很低,但是这道题还存在时间复杂度更低的解法。
为了找到中位数,需要在数组 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 中分别找到分割点 cut 1 \textit{cut}_1 cut1 和 cut 2 \textit{cut}_2 cut2,将每个数组分割成两个部分。
-
数组 nums 1 \textit{nums}_1 nums1 被分割成下标范围 [ 0 , cut 1 − 1 ] [0, \textit{cut}_1 - 1] [0,cut1−1] 和下标范围 [ cut 1 , m − 1 ] [\textit{cut}_1, m - 1] [cut1,m−1] 两部分,左边部分的长度是 cut 1 \textit{cut}_1 cut1。
-
数组 nums 2 \textit{nums}_2 nums2 被分割成下标范围 [ 0 , cut 2 − 1 ] [0, \textit{cut}_2 - 1] [0,cut2−1] 和下标范围 [ cut 2 , n − 1 ] [\textit{cut}_2, n - 1] [cut2,n−1] 两部分,左边部分的长度是 cut 2 \textit{cut}_2 cut2。
其中, 0 ≤ cut 1 ≤ m 0 \le \textit{cut}_1 \le m 0≤cut1≤m, 0 ≤ cut 2 ≤ n 0 \le \textit{cut}_2 \le n 0≤cut2≤n,即每个数组分割成的两个部分中可以有一个部分为空。
假设 nums 1 [ − 1 ] = nums 2 [ − 1 ] = − ∞ \textit{nums}_1[-1] = \textit{nums}_2[-1] = -\infty nums1[−1]=nums2[−1]=−∞, nums 1 [ m ] = nums 2 [ n ] = + ∞ \textit{nums}_1[m] = \textit{nums}_2[n] = +\infty nums1[m]=nums2[n]=+∞,分割应满足以下两个条件。
-
两个数组的左边部分的最大值小于等于两个数组的右边部分的最小值, max ( nums 1 [ cut 1 − 1 ] , nums 2 [ cut 2 − 1 ] ) ≤ min ( nums 1 [ cut 1 ] , nums 2 [ cut 2 ] ) \max(\textit{nums}_1[\textit{cut}_1 - 1], \textit{nums}_2[\textit{cut}_2 - 1]) \le \min(\textit{nums}_1[\textit{cut}_1], \textit{nums}_2[\textit{cut}_2]) max(nums1[cut1−1],nums2[cut2−1])≤min(nums1[cut1],nums2[cut2])。
-
两个数组的左边部分的长度之和为两个数组的长度之和的一半向上取整, cut 1 + cut 2 = ⌈ m + n 2 ⌉ \textit{cut}_1 + \textit{cut}_2 = \Big\lceil \dfrac{m + n}{2} \Big\rceil cut1+cut2=⌈2m+n⌉。
将两个数组的左边部分统称为前半部分,将两个数组的右边部分统称为后半部分,则前半部分的最大值小于等于后半部分的最小值,前半部分的元素个数为两个数组的长度之和的一半向上取整。
用 total = m + n \textit{total} = m + n total=m+n 表示两个升序数组的长度之和,用 lowerSize = ⌈ total 2 ⌉ \textit{lowerSize} = \Big\lceil \dfrac{\textit{total}}{2} \Big\rceil lowerSize=⌈2total⌉ 表示前半部分的元素个数。当 total \textit{total} total 是奇数时,中位数是前半部分的最大值;当 total \textit{total} total 是偶数时,中位数是前半部分的最大值与后半部分的最小值的平均数。
由于已知 cut 1 + cut 2 = lowerSize \textit{cut}_1 + \textit{cut}_2 = \textit{lowerSize} cut1+cut2=lowerSize,因此可以在 nums 1 \textit{nums}_1 nums1 中寻找 cut 1 \textit{cut}_1 cut1,当 cut 1 \textit{cut}_1 cut1 确定之后 cut 2 \textit{cut}_2 cut2 也可以确定。
寻找 cut 1 \textit{cut}_1 cut1 可以使用二分查找实现。由于两个数组都是升序数组, nums 1 [ cut 1 − 1 ] ≤ nums 1 [ cut 1 ] \textit{nums}_1[\textit{cut}_1 - 1] \le \textit{nums}_1[\textit{cut}_1] nums1[cut1−1]≤nums1[cut1] 和 nums 2 [ cut 2 − 1 ] ≤ nums 2 [ cut 2 ] \textit{nums}_2[\textit{cut}_2 - 1] \le \textit{nums}_2[\textit{cut}_2] nums2[cut2−1]≤nums2[cut2] 都满足,因此只需要满足 nums 1 [ cut 1 − 1 ] ≤ nums 2 [ cut 2 ] \textit{nums}_1[\textit{cut}_1 - 1] \le \textit{nums}_2[\textit{cut}_2] nums1[cut1−1]≤nums2[cut2] 和 nums 2 [ cut 2 − 1 ] ≤ nums 1 [ cut 1 ] \textit{nums}_2[\textit{cut}_2 - 1] \le \textit{nums}_1[\textit{cut}_1] nums2[cut2−1]≤nums1[cut1] 即可。二分查找需要查找满足 nums 1 [ cut 1 − 1 ] ≤ nums 2 [ cut 2 ] \textit{nums}_1[\textit{cut}_1 - 1] \le \textit{nums}_2[\textit{cut}_2] nums1[cut1−1]≤nums2[cut2] 的最大下标 cut 1 \textit{cut}_1 cut1。
用 low \textit{low} low 和 high \textit{high} high 分别表示二分查找的下标范围的下界和上界,初始时 low = 0 \textit{low} = 0 low=0, high = m \textit{high} = m high=m。每次查找时,取 index 1 \textit{index}_1 index1 为 low \textit{low} low 和 high \textit{high} high 的平均数向上取整,并得到 index 2 = lowerSize − index 1 \textit{index}_2 = \textit{lowerSize} - \textit{index}_1 index2=lowerSize−index1,比较 nums 1 [ index 1 − 1 ] \textit{nums}_1[\textit{index}_1 - 1] nums1[index1−1] 和 nums 2 [ index 2 ] \textit{nums}_2[\textit{index}_2] nums2[index2] 的大小关系,调整查找的下标范围。
-
如果 nums 1 [ index 1 − 1 ] ≤ nums 2 [ index 2 ] \textit{nums}_1[\textit{index}_1 - 1] \le \textit{nums}_2[\textit{index}_2] nums1[index1−1]≤nums2[index2],则 cut 1 ≥ index 1 \textit{cut}_1 \ge \textit{index}_1 cut1≥index1,因此在下标范围 [ index 1 , high ] [\textit{index}_1, \textit{high}] [index1,high] 中继续查找。
-
如果 nums 1 [ index 1 − 1 ] > nums 2 [ index 2 ] \textit{nums}_1[\textit{index}_1 - 1] > \textit{nums}_2[\textit{index}_2] nums1[index1−1]>nums2[index2],则 cut 1 < index 1 \textit{cut}_1 < \textit{index}_1 cut1<index1,因此在下标范围 [ low , index 1 − 1 ] [\textit{low}, \textit{index}_1 - 1] [low,index1−1] 中继续查找。
当 low = high \textit{low} = \textit{high} low=high 时,查找结束,此时 low \textit{low} low 即为 cut 1 \textit{cut}_1 cut1。
得到 cut 1 \textit{cut}_1 cut1 之后即可得到 cut 2 \textit{cut}_2 cut2, nums 1 [ cut 1 − 1 ] \textit{nums}_1[\textit{cut}_1 - 1] nums1[cut1−1] 和 nums 2 [ cut 2 − 1 ] \textit{nums}_2[\textit{cut}_2 - 1] nums2[cut2−1] 中的最大值是前半部分的最大值, nums 1 [ cut 1 ] \textit{nums}_1[\textit{cut}_1] nums1[cut1] 和 nums 2 [ cut 2 ] \textit{nums}_2[\textit{cut}_2] nums2[cut2] 中的最小值是后半部分的最小值。根据前半部分的最大值和后半部分的最小值即可计算中位数。
-
当 total \textit{total} total 是奇数时,中位数是前半部分的最大值。
-
当 total \textit{total} total 是偶数时,中位数是前半部分的最大值与后半部分的最小值的平均数。
该解法的时间复杂度是 O ( log m ) O(\log m) O(logm),优于解法一的 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n))。
实现方面,由于只需要在一个数组中二分查找,因此可以选择较短的数组二分查找,时间复杂度是 O ( log min ( m , n ) ) O(\log \min(m, n)) O(logmin(m,n))。
以下用一个例子说明上述过程。
两个数组是 nums 1 = [ 1 , 2 , 3 , 4 , 5 ] \textit{nums}_1 = [1, 2, 3, 4, 5] nums1=[1,2,3,4,5], nums 2 = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] \textit{nums}_2 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] nums2=[1,2,3,4,5,6,7,8,9,10],两个数组的长度分别是 m = 5 m = 5 m=5, n = 10 n = 10 n=10,长度之和是 15 15 15,前半部分的元素个数是 8 8 8。初始时, low = 0 \textit{low} = 0 low=0, high = 5 \textit{high} = 5 high=5。
-
根据 low = 0 \textit{low} = 0 low=0 和 high = 5 \textit{high} = 5 high=5 计算得到 index 1 = 3 \textit{index}_1 = 3 index1=3, index 2 = 5 \textit{index}_2 = 5 index2=5。由于 nums 1 [ 2 ] ≤ nums 2 [ 5 ] \textit{nums}_1[2] \le \textit{nums}_2[5] nums1[2]≤nums2[5],因此将 low \textit{low} low 更新为 3 3 3。
-
根据 low = 3 \textit{low} = 3 low=3 和 high = 5 \textit{high} = 5 high=5 计算得到 index 1 = 4 \textit{index}_1 = 4 index1=4, index 2 = 4 \textit{index}_2 = 4 index2=4。由于 nums 1 [ 3 ] ≤ nums 2 [ 4 ] \textit{nums}_1[3] \le \textit{nums}_2[4] nums1[3]≤nums2[4],因此将 low \textit{low} low 更新为 4 4 4。
-
根据 low = 4 \textit{low} = 4 low=4 和 high = 5 \textit{high} = 5 high=5 计算得到 index 1 = 5 \textit{index}_1 = 5 index1=5, index 2 = 3 \textit{index}_2 = 3 index2=3。由于 nums 1 [ 4 ] > nums 2 [ 3 ] \textit{nums}_1[4] > \textit{nums}_2[3] nums1[4]>nums2[3],因此将 high \textit{high} high 更新为 4 4 4。
-
此时 low = high \textit{low} = \textit{high} low=high,二分查找结束。根据 low = 4 \textit{low} = 4 low=4 计算得到 cut 1 = 4 \textit{cut}_1 = 4 cut1=4, cut 2 = 4 \textit{cut}_2 = 4 cut2=4,前半部分的最大值是 4 4 4,后半部分的最小值是 5 5 5。由于两个数组的长度之和是奇数,因此中位数是前半部分的最大值,中位数是 4 4 4。
代码
class Solution {public double findMedianSortedArrays(int[] nums1, int[] nums2) {return nums1.length <= nums2.length ? findMedian(nums1, nums2) : findMedian(nums2, nums1);}public double findMedian(int[] shorter, int[] longer) {int length1 = shorter.length, length2 = longer.length;int total = length1 + length2;int lowerSize = (total + 1) / 2;int low = 0, high = length1;while (low < high) {int index1 = low + (high - low + 1) / 2;int index2 = lowerSize - index1;int left1 = shorter[index1 - 1];int right2 = longer[index2];if (left1 <= right2) {low = index1;} else {high = index1 - 1;}}int cut1 = low, cut2 = lowerSize - low;int lower1 = cut1 == 0 ? Integer.MIN_VALUE : shorter[cut1 - 1];int lower2 = cut2 == 0 ? Integer.MIN_VALUE : longer[cut2 - 1];int higher1 = cut1 == length1 ? Integer.MAX_VALUE : shorter[cut1];int higher2 = cut2 == length2 ? Integer.MAX_VALUE : longer[cut2];int lowerMax = Math.max(lower1, lower2), higherMin = Math.min(higher1, higher2);if (total % 2 == 1) {return lowerMax;} else {return (lowerMax + higherMin) / 2.0;}}
}
复杂度分析
-
时间复杂度: O ( log min ( m , n ) ) O(\log \min(m, n)) O(logmin(m,n)),其中 m m m 和 n n n 分别是数组 nums 1 \textit{nums}_1 nums1 和 nums 2 \textit{nums}_2 nums2 的长度。在较短的数组中二分查找,范围是 [ 0 , min ( m , n ) ] [0, \min(m, n)] [0,min(m,n)],二分查找的次数是 O ( log min ( m , n ) ) O(\log \min(m, n)) O(logmin(m,n)),每次查找的时间是 O ( 1 ) O(1) O(1),因此时间复杂度是 O ( log min ( m , n ) ) O(\log \min(m, n)) O(logmin(m,n))。
-
空间复杂度: O ( 1 ) O(1) O(1)。
相关文章:

二分查找题目:寻找两个正序数组的中位数
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:寻找两个正序数组的中位数 出处:4. 寻找两个正序数组的中位数 难度 8 级 题目描述 要求 给定两个大…...
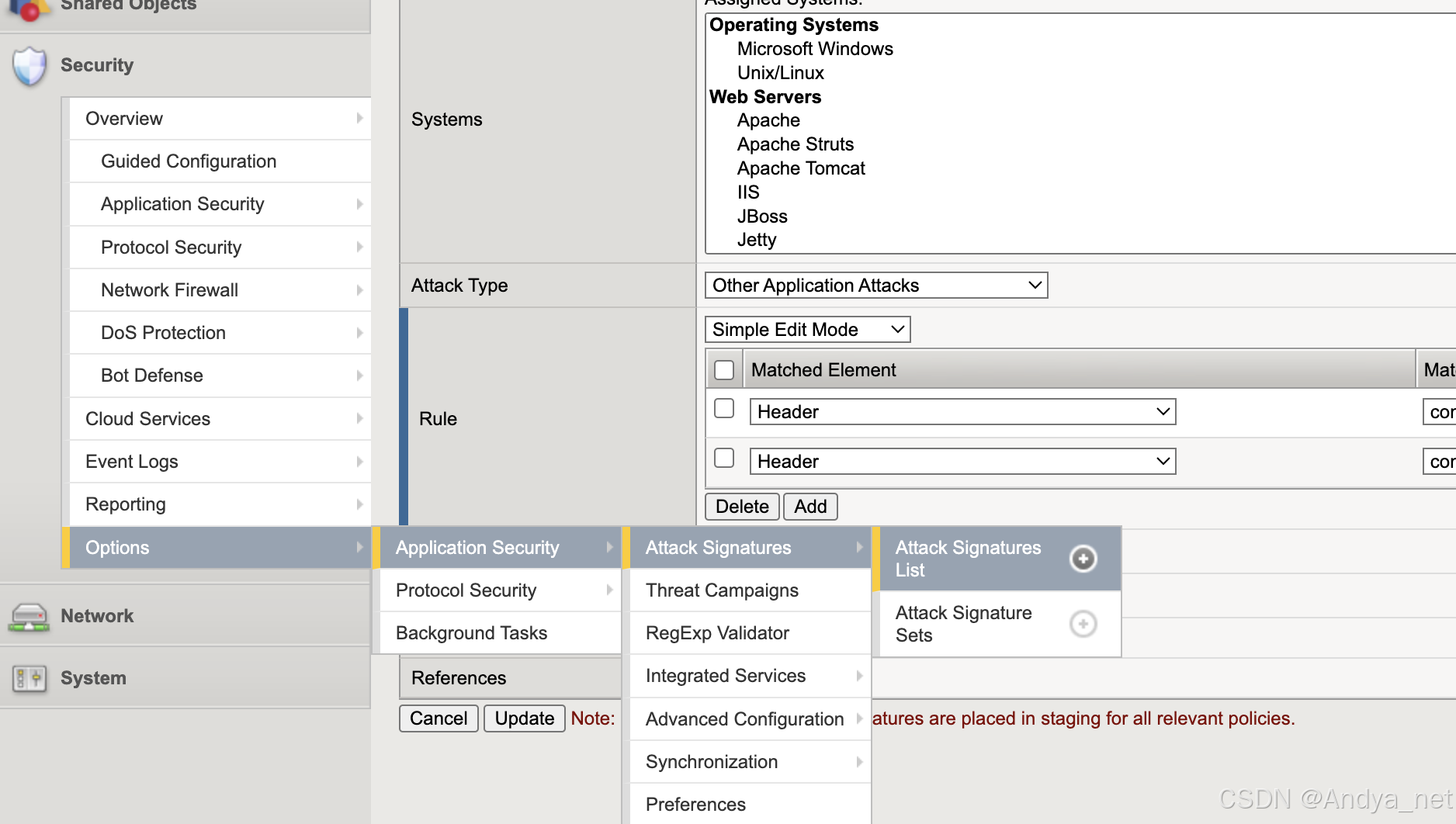
网络安全 | F5-Attack Signatures详解
关注:CodingTechWork 关于攻击签名 攻击签名是用于识别 Web 应用程序及其组件上攻击或攻击类型的规则或模式。安全策略将攻击签名中的模式与请求和响应的内容进行比较,以查找潜在的攻击。有些签名旨在保护特定的操作系统、Web 服务器、数据库、框架或应…...
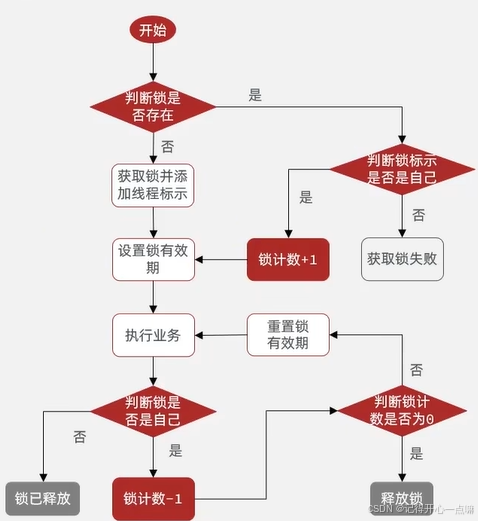
Redis --- 分布式锁的使用
我们在上篇博客高并发处理 --- 超卖问题一人一单解决方案讲述了两种锁解决业务的使用方法,但是这样不能让锁跨JVM也就是跨进程去使用,只能适用在单体项目中如下图: 为了解决这种场景,我们就需要用一个锁监视器对全部集群进行监视…...

LeetCode100之全排列(46)--Java
1.问题描述 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案 示例1 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例2 输入:nums [0,1] 输出…...

goframe 博客分类文章模型文档 主要解决关联
goframe 博客文章模型文档 模型结构 (BlogArticleInfoRes) BlogArticleInfoRes 结构体代表系统中的一篇博客文章,包含完整的元数据和内容管理功能。 type BlogArticleInfoRes struct {Id uint orm:"id,primary" json:"id" …...

【JavaWeb06】Tomcat基础入门:架构理解与基本配置指南
文章目录 🌍一. WEB 开发❄️1. 介绍 ❄️2. BS 与 CS 开发介绍 ❄️3. JavaWeb 服务软件 🌍二. Tomcat❄️1. Tomcat 下载和安装 ❄️2. Tomcat 启动 ❄️3. Tomcat 启动故障排除 ❄️4. Tomcat 服务中部署 WEB 应用 ❄️5. 浏览器访问 Web 服务过程详…...

安卓日常问题杂谈(一)
背景 关于安卓开发中,有很多奇奇怪怪的问题,有时候这个控件闪一下,有时候这个页面移动一下,这些对于快速开发中,去查询,都是很耗费时间的,因此,本系列文章,旨在记录安卓…...

Kitchen Racks 2
Kitchen Racks 2 吸盘置物架 Kitchen Racks-CSDN博客...

嵌入式学习笔记-杂七杂八
文章目录 连续波光纤耦合激光器工作原理主要特点应用领域设计考虑因素 数值孔径(Numerical Aperture,简称NA)数值孔径的定义数值孔径的意义数值孔径的计算示例数值孔径与光纤 四象限探测器检测目标方法四象限划分检测目标的步骤1. 数据采集2.…...
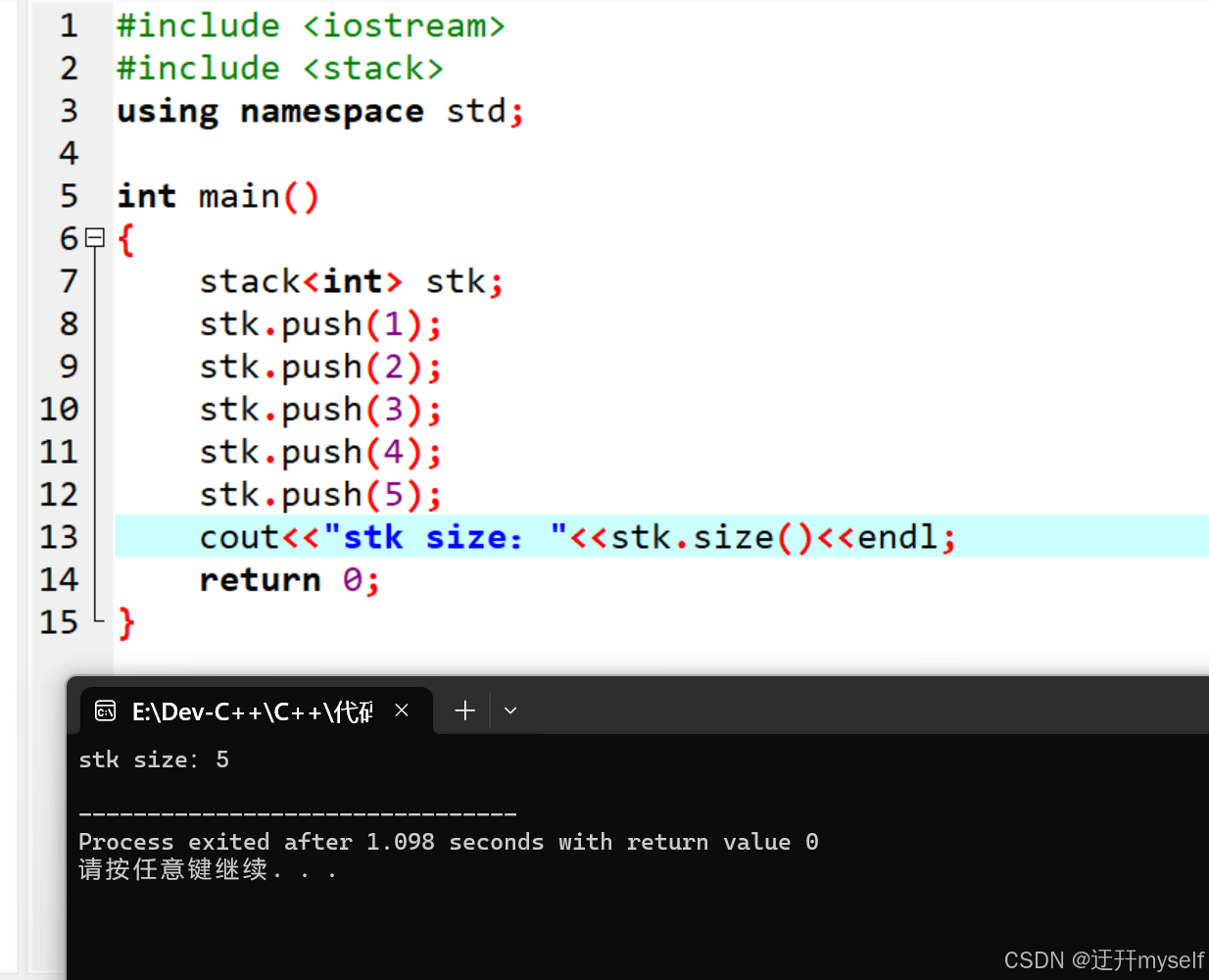
14-7C++STL的stack容器
(一)stack容器的入栈与出栈 (1)stack容器的简介 stack堆栈容器,“先进后出”的容器,且stack没有迭代器 (2)stack对象的默认构造 stack采用模板类实现,stack对象的默认…...

Vue 3 中的响应式系统:ref 与 reactive 的对比与应用
Vue 3 的响应式系统是其核心特性之一,它允许开发者以声明式的方式构建用户界面。Vue 3 引入了两种主要的响应式 API:ref 和 reactive。本文将详细介绍这两种 API 的用法、区别以及在修改对象属性和修改整个对象时的不同表现,并提供完整的代码…...

物业巡更系统助推社区管理智能化与服务模式创新的研究与应用
内容概要 在现代社区管理中,物业巡更系统扮演着至关重要的角色。首先,我们先来了解一下这个系统的概念与发展背景。物业巡更系统,顾名思义,是一个用来提升物业管理效率与服务质量的智能化工具。随着科技的发展,传统的…...

windows蓝牙驱动开发-生成和发送蓝牙请求块 (BRB)
以下过程概述了配置文件驱动程序生成和发送蓝牙请求块 (BRB) 应遵循的一般流程。 BRB 是描述要执行的蓝牙操作的数据块。 生成和发送 BRB 分配 IRP。 分配BRB,请调用蓝牙驱动程序堆栈导出以供配置文件驱动程序使用的 BthAllocateBrb 函数。;初始化 BRB…...
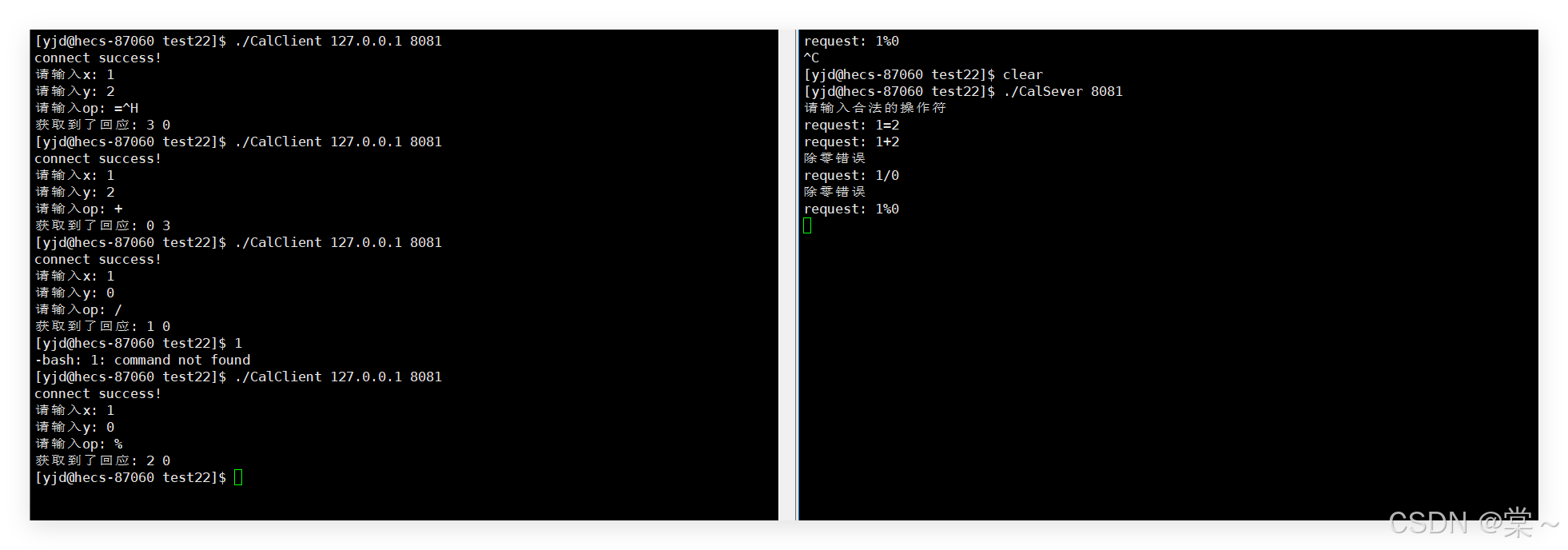
Linux网络之序列化和反序列化
目录 序列化和反序列化 上期我们学习了基于TCP的socket套接字编程接口,并实现了一个TCP网络小程序,本期我们将在此基础上进一步延伸学习,实现一个网络版简单计算器。 序列化和反序列化 在生活中肯定有这样一个情景。 上图大家肯定不陌生&a…...
linux设置mysql远程连接
首先保证服务器开放了mysql的端口 然后输入 mysql -u root -p 输入密码后即可进入mysql 然后再 use mysql; select user,host from user; update user set host"%" where user"root"; flush privileges; 再执行 select user,host from user; 即可看到变…...

react-native网络调试工具Reactotron保姆级教程
在React Native开发过程中,调试和性能优化是至关重要的环节。今天,就来给大家分享一个非常强大的工具——Reactotron,它就像是一个贴心的助手,能帮助我们更轻松地追踪问题、优化性能。下面就是一份保姆级教程哦! 一、…...

erase() 【删数函数】的使用
**2025 - 01 - 25 - 第 48 篇 【函数的使用】 作者(Author) 文章目录 earse() - 删除函数一. vector中的 erase1 移除单个元素2 移除一段元素 二. map 中的erase1 通过键移除元素2 通过迭代器移除元素 earse() - 删除函数 一. vector中的 erase vector 是一个动态数组&#x…...

性能测试丨内存火焰图 Flame Graphs
内存火焰图的基本原理 内存火焰图是通过分析堆栈跟踪数据生成的一种图形化表现,能够展示应用程序在运行时各个函数的内存占用情况。火焰图的宽度代表了函数占用的内存量,而火焰的高度则显示了函数在调用栈中的层级关系。通过这种可视化方式,…...
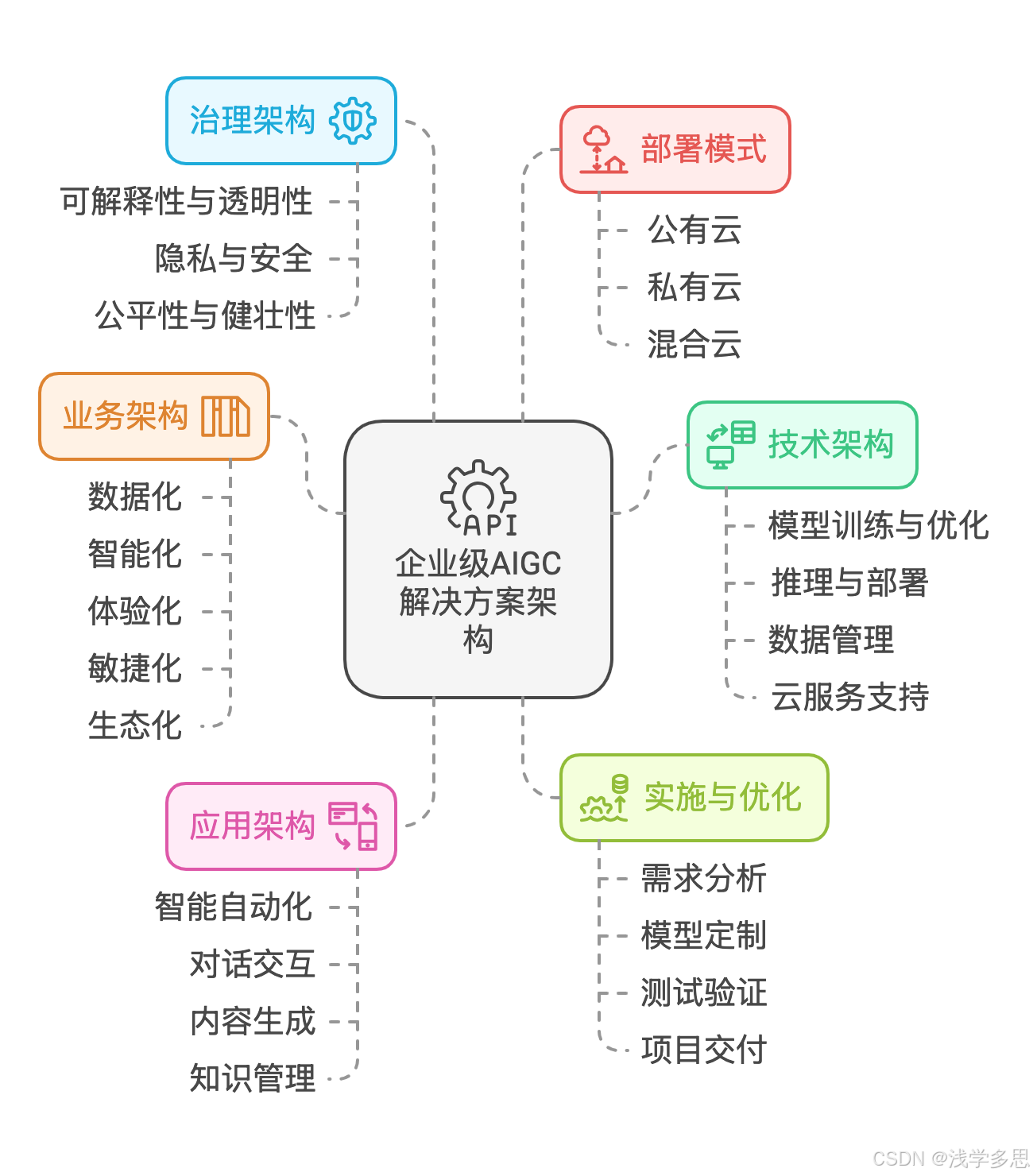
AIGC的企业级解决方案架构及成本效益分析
AIGC的企业级解决方案架构及成本效益分析 一,企业级解决方案架构 AIGC(人工智能生成内容)的企业级解决方案架构是一个多层次、多维度的复杂系统,旨在帮助企业实现智能化转型和业务创新。以下是总结的企业级AIGC解决方案架构的主要组成部分: 1. 技术架构 企业级AIGC解决方…...

Linux 入门 常用指令 详细版
欢迎来到指令小仓库!! 宝剑锋从磨砺出,梅花香自苦寒来 什么是指令? 指令和可执行程序都是可以被执行的-->指令就是可执行程序。 指令一定是在系统的每一个位置存在的。 1.ls指令 语法: ls [选项][目…...

【R语言】流程控制
R语言中,常用的流程控制函数有:repeat、while、for、if…else、switch。 1、repeat循环 repeat函数经常与 break 语句或 next 语句一起使用。 repeat ({x <- sample(c(1:7),1)message("x ", x, ",你好吗?")if (x …...
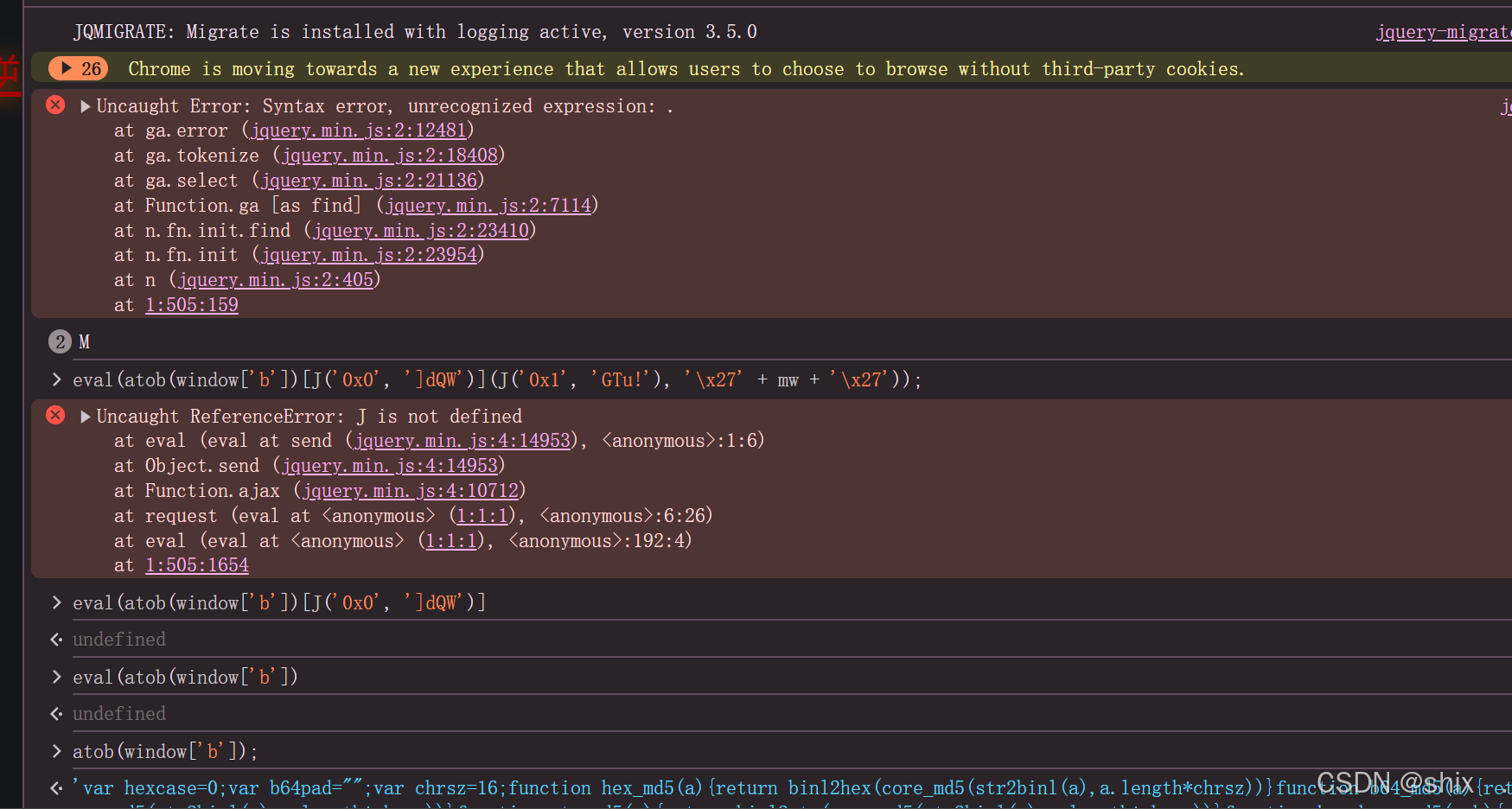
猿人学第一题 js混淆源码乱码
首先检查刷新网络可知,m参数被加密,这是一个ajax请求 那么我们直接去定位该路径 定位成功 观察堆栈之后可以分析出来这应该是一个混淆,我们放到解码平台去还原一下 window["url"] "/api/match/1";request function…...
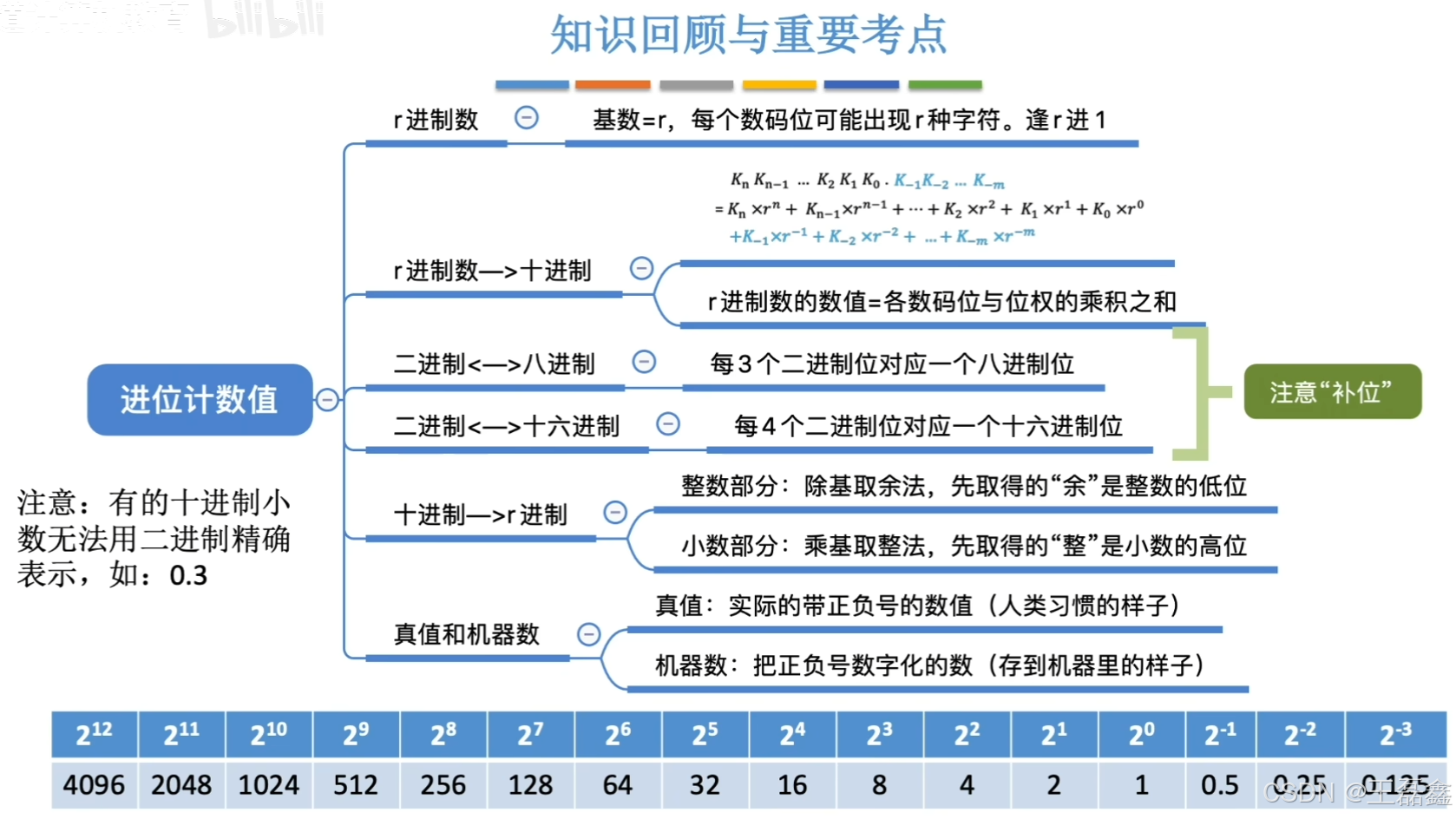
计算机组成原理(2)王道学习笔记
数据的表示和运算 提问:1.数据如何在计算机中表示? 2.运算器如何实现数据的算术、逻辑运算? 十进制计数法 古印度人发明了阿拉伯数字:0,1,2,3,4,5,6&#…...

【AI日记】25.01.26
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】【AI日记】【读书与思考】 AI kaggle 比赛:Forecasting Sticker Sales 读书 书名:自由宪章 律己 AI:6 小时作息:00:30-8:30短视频:大于 1 小时读书和写作&a…...

三. Redis 基本指令(Redis 快速入门-03)
三. Redis 基本指令(Redis 快速入门-03) 文章目录 三. Redis 基本指令(Redis 快速入门-03)1. Redis 基础操作:2. 对 key(键)操作:3. 对 DB(数据库)操作4. 最后: Reids 指定大全(指令文档): https://www.redis.net.cn/order/ Redis…...

设计模式的艺术-代理模式
结构性模式的名称、定义、学习难度和使用频率如下表所示: 1.如何理解代理模式 代理模式(Proxy Pattern):给某一个对象提供一个代理,并由代理对象控制对原对象的引用。代理模式是一种对象结构型模式。 代理模式类型较多…...

C#新语法
目录 顶级语句(C#9.0) using 全局using指令(C#10.0) using资源管理问题 using声明(C#8.0) using声明陷阱 错误写法 正确写法 文件范围的命名空间声明(C#10.0) 可空引用类型…...

微信小程序压缩图片
由于wx.compressImage(Object object) iOS 仅支持压缩 JPG 格式图片。所以我们需要做一下特殊的处理: 1.获取文件,判断文件是否大于设定的大小 2.如果大于则使用canvas进行绘制,并生成新的图片路径 3.上传图片 async chooseImage() {let …...
通义灵码插件保姆级教学-IDEA(安装及使用)
一、JetBrains IDEA 中安装指南 官方下载指南:通义灵码安装教程-阿里云 步骤 1:准备工作 操作系统:Windows 7 及以上、macOS、Linux; 下载并安装兼容的 JetBrains IDEs 2020.3 及以上版本,通义灵码与以下 IDE 兼容&…...
windows下本地部署安装hadoop+scala+spark-【不需要虚拟机】
注意版本依赖【本实验版本如下】 Hadoop 3.1.1 spark 2.3.2 scala 2.11 1.依赖环境 1.1 java 安装java并配置环境变量【如果未安装搜索其他教程】 环境验证如下: C:\Users\wangning>java -version java version "1.8.0_261" Java(TM) SE Runti…...
