石家庄网站建设与推广/常用的网络推广的方法有哪些

1我们之前学了二叉树的顺序存储（这种顺序存储的二叉树被称为堆），我们今天来学习一下二叉树的链式存储：

我们使用链表来表示一颗二叉树：

⽤链表来表⽰⼀棵⼆叉树，即⽤链来指⽰元素的逻辑关系。通常的⽅法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别⽤来给出该结点左孩⼦和右孩⼦所在的链结点的存储地址。

比如这就是我们的二叉树的链式存储，跟链表是不是比较像，就是使用链表来进行存储我们的二叉树；

但是我想你也一定发现了我们使用链式存储的二叉树不一定是完全的二叉树；

我们之前在讲堆的时候，我们的二叉树使用的一定是完全二叉树；因为我们的堆的话，使用的是顺序存储，使用完全二叉树的话，可以节省我们的内存空间；

但是我们的二叉树在进行链式存储的时候，没有这个要求；我们可以是完全二叉树，也可以是其他的二叉树，没有什么要求；

我们的链式存储，我们该怎样定义我们的结点呢？

我们可以知道，我们的二叉树的度最大为2，最小为0，所以，我们就设置两个指针，一个左指针，还有一个右指针；分别指向我们的左孩子和右孩子；

这就是我们的二叉树的结点的定义；

二叉树的前中后序遍历：

对二叉树的操作离不开二叉树的遍历，我们来看一下二叉树的遍历；

前序遍历：先遍历根节点，在遍历左子树，最后便利右子树；

中序遍历：先遍历左子树，在遍历根节点，最后遍历右子树；

后序遍历：先遍历左子树，在遍历右子树，最后便利根节点；

//我们的前中后分别表示的是根节点的位置，前就表示根节点在第一个位置，中就表示根节点在中间位置，后就表示根节点在最后面的位置。

接下来我们来实现一下前序遍历的代码；

这就是我们的前序遍历；我们在函数里面进行递归调用；我们先把我们的根节点的数据进行打印，然后遍历我们的左子树，然后遍历右子树；当我们遇到的结点的数据是NULL的时候，我们打印并返回；

接下来我们来实现一下中序遍历：

这个就是我们的中序遍历，当然，你可以发现，他和前序遍历是比较像的，我们只是改变了位置，我们先进行了左子树的遍历，然后当我们的左子树一直下去知道是空的时候，我们返回，然后打印我们的这课子树的根节点，然后再进行这棵树的右孩子的遍历；这样不断地递归；

这就是我们的中序遍历的结果；

接下来我们来看后序遍历：

12

这就是我们的后序遍历，我们还是可以发现，那就是我们的基本代码还是没有什么大的改变；我们还是只是改变了原来代码的顺序，我们先让左子树进行遍历，左子树无限的递归，直到左子树的尽头，然后在左子树的尽头我们先遍历右子树，然后打印我们的根节点。

这就是我们的结果；

然后我们来实现一下有关二叉树的代码的实现，但是我们在这里对二叉树的插入操作这一些并不进行讲解，因为我们进行链式存储的二叉树并不是完全二叉树，只要是二叉树的话都可以进行链式存储，这样的话，我们的二叉树的插入位置就是非常多了，这就没有了限制，这就不是很好，等到我们后面学习的红黑树，平衡树的话，这些对二叉树的插入操作是有限制的，我们就可以实现一下插入操作；

我们先来实现一下：计算二叉树的结点个数；

计算二叉树的结点的个数有两种方法：

第一种的话，我们对二叉树进行遍历，然后设置计数器，之前我们遇到根节点的话，我们就打印数据，这下我们不打印数据，我们让计数器+1，遇到空结点的话，我们不操作计数器，但是这时候就出现问题了，我们的size计数器不知道是使用局部变量还是全局变量，这两个都不行，局部变量的话，因为我们遍历树我们的函数要不断地进行递归，我们每次进入我们的函数的话，我们的计数器都会被清零。。那我们使用全局变量呢？也不行，全局变量看着好像可以，每次进入函数的话，我们的计数器没有被清零，但是有一个问题，那就是我们的全局变量，在我们递归调用遍历完我们的二叉树的时候，我们的全局变量没有变化，这就导致我们再一次调用我们的二叉树的时候，size就加倍了，这就累加了，那怎么办呢？我们还有方法就是我们不设置计数器了，我们直接使用递归来进行。

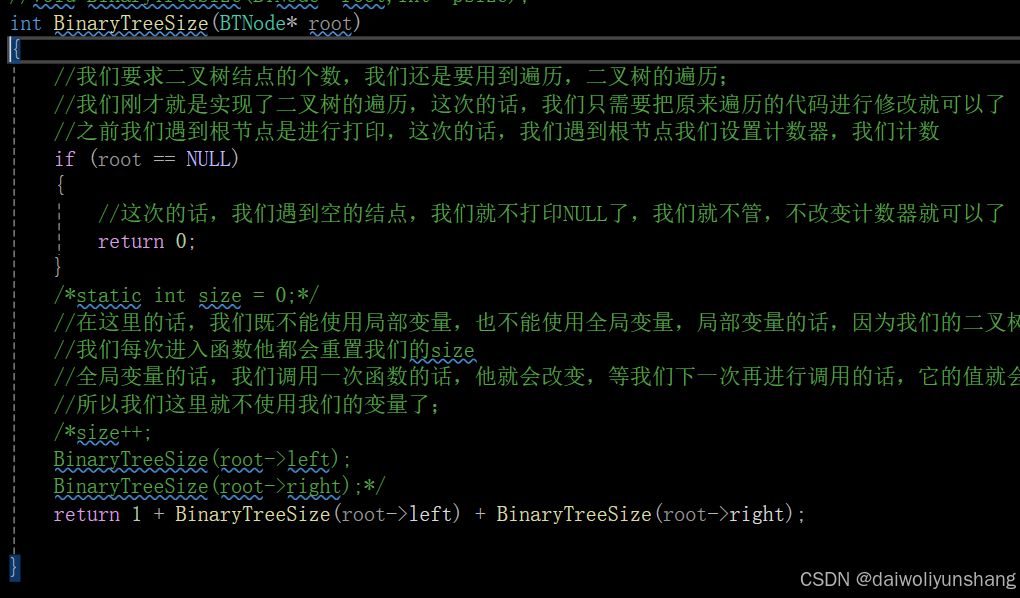
实际的代码只有几行，我们进行判断，如果是空的的话，我们就返回0，但是如果不是空的的话，我们就返回1+判断根节点的左右子树；

我们然后来继续看我们的下一个要实现的方法：

二叉树的叶子结点的个数：

我们要求二叉树里面叶子结点的个数，那我们就要判断一下我们遍历到的这个结点是不是叶子节点，那么我们要怎样判断他是不是叶子节点呢？我们就看他的两个孩子是不是NULL，如果他的两个孩子都是NULL的话，我们就说这个结点是一个叶子节点。

我们在进行遍历的时候，我们就看他是不是叶子结点，如果是叶子节点的话，我们就返回1，不是叶子节点的话，如果是根节点或者是空的结点，我们就不管，或者返回0，然后我们还是使用遍历

我们来看我们的代码，进入到我们的函数里面以后，我们先判断它是不是空的结点，如果是空的结点的话，这就不是叶子节点，我们返回0，然后的话，我们就再次进行遍历，和我们的第一个判断结点个数其实是比较次相似的，我们判断它的结点的个数的时候，我们先进行判断看他是不是NULL，不是的话，我们进行return的时候进行+1，因为一颗正常的二叉树，（在进行链式存储的时候不需要是完全二叉树），我们如果可以遍历到的话，他不是NULL，就是一个正常的结点，  所以我们要统计结点的个数的话，我们就+1，然后遍历这个结点的左子树和右子树，然后不断的递归调用我们的函数，最终就可以得到我们的二叉树的节点的个数，这里的话，我们就不+1了，我们进行额外的叶子节点的判定。

二叉树第K层结点的个数:

这里的话，我们就传两个参数，我们的第一个参数还是我们的二叉树的根节点，当然我们传的还是一级指针的，我们不需要修改我们的二叉树，我们传一级指针就可以了，然后我们的第二个参数，我们就传一个计数器，我们传一个k，我们不断地让k--，当我们的k等于1的时候，就来到了我们的第k层然后我们遍历到k等于1的结点的时候，我们就返回1。

我们来看我们的代码，我们进入到我们的函数，我们先判断是不是NULL，是的话我们就返回0，因为我们的链式存储的二叉树不要求是完全二叉树，所以还没到第k层的时候就先出现了NULL，所以我们还是要对NULL进行一下判断，是NULL的话，我们就返回0，不是的话，我们就继续，这时候我们可以继续进行就说明我们的这个结点他不是NULL，所以的话，我们就判断一下他是不是第k层就可以了，是的话，我们就返回1，然后我们的return还是和之前一样，我们直接进行他的左右子树的判断，进行不断的递归判断。

求二叉树的深度或者高度:

我们还是要根据递归的思想来进行判断,首先我们开始的时候进入的就是根节点，然后根节点不是NULL，然后我们就继续，我们就求他的左子树的大小，然后我们再求右子树的大小，然后我们1+一个三目操作符，判断左右子树哪个比较大，加的1就是我们的根节点，

我们来看我们的函数，我们进入我们的函数，进入到函数里面以后我们还是遇到NULL的话，我们返回0，然后的话，我们就根据我们的思路，我们先把左子树的高度求出来，然后把右子树的高度求出来，然后return 1+左右子树里面比较大的那个，我们在求他的左右子树的时候，我们还是使用我们的这个函数，假如我们要求这个左子树的高度的时候，我们就求这个左子树的左子树的高度和右子树的高度，然后return 1+比较大的子树，然后这就是我们的左子树，我们就这样不断地进行递归，直到我们的左右子树变成NULL的时候，我们就递归到尽头了。这时候就返回，我们就可以求出我们的二叉树的高度。

然后接下来我们要实现的是，

查找二叉树节点值为x的结点:

我们直接来看我们的代码：

当然，我们这次函数的传值传的还是两个参数，第一个参数为根节点，第二个参数是我们的x值，进入到函数里面，我们还是遇到NULL的结点的时候，我们就返回NULL，如果他不是NULL的话，我们就判断这个非空的结点的data是不是x，如果这个结点的数据恰好就是我们的x的话，我们就返回这个结点，但是如果这个结点的x不是我们要求的x的话，我们就看他的左孩子是不是我们要求的x，我们再次进入到我们的函数里面，我们先进行判空，如果不是NULL的话，我们就看他的data是不是我们要求的x，如果是的话，我们就返回，然后返回到我们的第一个函数里面，然后我们把返回值存起来，判断它是不是NULL，如果不是NULL的话，我们就把他返回，在这里可能你觉得有点草率，（你可能会说，我们只进行判空，那会不会返回的虽然不是NULL，但是有可能是其他的不是data为x的结点呢？），但是其实你继续看，当我们的结点的左孩子不是NULL，并且左孩子的数据的data不是我们的x的话，我们的函数就不会返回他，我们就会判断我们的这个左孩子的左孩子，看他是不是，我们一定是不会返回我们的无效的数据的，我们看我们的函数，我们进行返回的条件一定是他为NULL，或者不为NULL，但是他的data为x，这时候我们才会进行返回，至于下面的两个左右孩子我们其实就是函数进行递归，我们的返回的条件永远是不变的。。

接下来我们来看

二叉树的销毁：

直接来看我们的代码，我们可以很清楚的发现，我们的函数的参数是一个二级指针，为什么这里是二级指针呢？

因为这里的话，我们是要改变我们的结点了,我们的一级指针就可以代表我们的结点，我们要修改我们的结点，就相当于是修改一级指针，所以这里我们要传二级指针。

然后我们看我们的函数，我们进入到我们的函数里面，还是我们先判断我们的结点是不是NULL，如果是的话，我们就出节点，什么都不返回直接return就可以，但是如果我们得这个不是NULL的话，我们就要进行遍历销毁我们的结点了，这里就有一个问题，我们是采用什么遍历方式，在这里的话，我们采用后序遍历，我们把根节点放在最后面进行删除，因为如果我们先删除根节点的话，我们的这个结点的左右孩子就找不到了，所以在这里我们只能使用后序遍历来进行销毁。

接下来我们来看下一个函数--

层序遍历：

什么是层序遍历呢？

之前我们学的前序遍历，中序遍历，后序遍历都是从左往右的进行遍历。

我们得层序遍历指的就是我们按层序的进行遍历，先是第一层，然后第二层的进行遍历，，，

就比如我们的这个二叉树，他进行遍历的结果就是A,B,C,D,E,F.

那我们该怎样才能实现我们的这个方法；

我们在这里可以创建一个队列来进行，

我们可以先把我们的第一个二叉树的结点放入到队列里面，然后取第一个结点，第一个结点出队列，然后把第一个结点的左右非空孩子入队列，然后继续取队头结点，然后把队头结点的左右孩子（非空孩子入队列）。

我们来看我们的函数，进入到我们的函数里面以后我们创建一个队列，然后初始化一个空的队列，然后把我们的根节点压入队列，，，，最后结束以后我们把我们的队列销毁；

接下来我们来看

判断是否为完全二叉树：

在这里我们判断一个二叉树是不是完全的二叉树，

我们来看我们的这个二叉树，这就不是一个完全二叉树，显然这是一个非完全的二叉树，他的数据就是不连续的，我们在进行层序遍历的时候，我们遍历的结果是 A,BC,D,NULL,E,F.  我们遍历完后的结果就是我们中间会有一个NULL，这样的数据就是不连续的，我们在实现我们的堆二叉树的时候，我们采用的是完全的二叉树，堆二叉树就是没有什么数据空间的浪费，他的数据是连续的，堆二叉树的底层就是一个数组，我们的这个链式存储底层成了链表；

所以我们就可以看这个二叉树的数据是不是连续的就可以了，所以我们在这里就还是使用我们的层序遍历来进行，我们的层序遍历就是按层的来进行遍历。

我们来看我们的非完全的二叉树层序遍历的结果就是当我们的队列取到空的结点以后，我们的队列里面还有非空的结点，这就是我们的非完全的二叉树。

但是我们的完全二叉树，我们的队列在取到NULL的时候，我们的队列里面的数据的结点就都是空的结点了。

我们来看我们的代码：