Leetcode:518. 零钱兑换 II(C++)
目录
518. 零钱兑换 II
问题描述:
实现代码与解析:
动态规划(完全背包):
原理思路:
377. 组合总和 Ⅳ
问题描述:
实现代码与解析:
动态规划(完全背包):
原理思路:
518. 零钱兑换 II
问题描述:
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5] 输出:4 解释:有四种方式可以凑成总金额: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2] 输出:0 解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10] 输出:1
实现代码与解析:
动态规划(完全背包):
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for(int i = 0; i < coins.size(); i++){for(int j = coins[i]; j <= amount; j++){dp[j] += dp[j - coins[i]];}}return dp[amount];}
};原理思路:
和Leetcode:494. 目标和(C++)_Cosmoshhhyyy的博客-CSDN博客很像,只不过一个是一个数只能用一次,而本题可以用多次,也就是完全背包求组合数的问题,完全背包的代码可以看看
动态规划:0-1背包、完全背包问题 | 详细原理解释 | 代码及优化(C++)_Cosmoshhhyyy的博客-CSDN博客_c++代码优化工具 两者结合一下就很好写出了,不再解释了,比较简单。
377. 组合总和 Ⅳ
问题描述:
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4 输出:7 解释: 所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) 请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3 输出:0
实现代码与解析:
动态规划(完全背包):
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for(int j = 0; j <= target; j++){for(int i = 0; i < nums.size(); i++){if(j >= nums[i] && dp[j] < INT_MAX - dp[j - nums[i]]){dp[j] += dp[j - nums[i]];} }} return dp[target];}
};原理思路:
此题与上题相似,放在一次主要是注意这两题的差别,此题强调的是顺序,不同顺序也是一个结果,而上一题顺序无所谓,只算一总结果。
先说结论吧,先遍历物品的话,就是上一题不用管顺序,先遍历背包的话,就是这题需要在意顺序。
注意这个 if 的判断阿,因为我们先遍历背包了,int j = nums[i] 的逻辑就只能放在这里了。
if(j >= nums[i])
{dp[j] += dp[j - nums[i]];
} 因为有一组测试数据相加超过int范围,所以就多加了一个dp[j] < INT_MAX - dp[j - nums[i]]的判断,其余不变。
相关文章:
)
Leetcode:518. 零钱兑换 II(C++)
目录 518. 零钱兑换 II 问题描述: 实现代码与解析: 动态规划(完全背包): 原理思路: 377. 组合总和 Ⅳ 问题描述: 实现代码与解析: 动态规划(完全背包࿰…...

Java中类是什么
类(class)是构造对象的模板或蓝图。 我们可以将类想象成制作小甜饼的模具,将对象想象为小甜饼。由类构造(construct)对象的过程称为创建类的实例(instance)。 正如前面所看到的,用Java 编写的所有代码都位于某个类里面。 标准 Java 库提供了几千个类&a…...
C进阶:预处理
🤖本篇文章主要讲解预处理的知识,即使你是小白也可以看的懂,若你对预处理有所不解,确定不来看看吗?😿 目录 一.代码运行是的两种环境 二.翻译环境 三.预定义符号 四.#define 1.define 定义宏 2.带有…...
侯捷C++系统工程师
前言我相信对于每一个学习C的同学和从业者来说,台湾著名学者侯捷老师的C系列都是不可错过的好视频。侯捷老师在网上已有五门课,分别是:C面向对象开发、STL标准库与泛型编程、C新标准C1&14、C内存管理机制以及C Startup揭秘讲师介绍侯捷老…...
ReentrantReadWriteLock、StampedLock
ReentrantLock、ReentrantReadWriteLock、StampedLock 读写锁 一个资源可以被多个读线程访问,或者被一个写线程访问,但是不能同时存在读写线程。 小口诀:读写互斥,读读共享 锁的演变 无锁-----> 独占锁----->读写锁---…...

Mysql中的事务、锁、日志详解
一、事务 1.事务特性及保证事务特性的原理 原子性:当前事务的操作要么全部成功,要么全部失败。原子性由undo log实现,undo log记录了每次操作之前的数据版本,如果某一操作失败,可以根据undo log回滚到最初状态。一致…...

k8s笔记24--安装metrics-server及错误处理
k8s笔记24--安装metrics-server及错误处理1 介绍2 安装3 常见错误第一次错误 持续 Failed probe第二次错误 bad status code "403 Forbidden"4 说明1 介绍 最近一个同事在老版本的 k8s 上安装metrics-server,pod一直处于running 非就绪状态,经…...
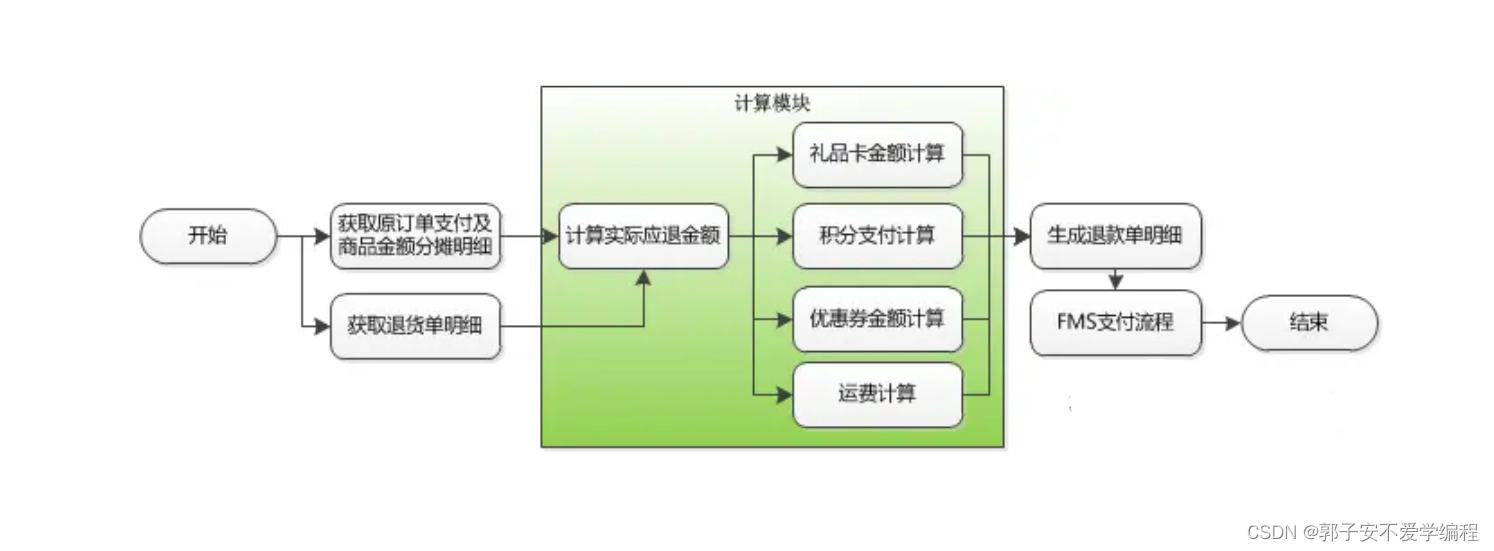
【电商】订单系统--售后的简易流程与系统关系
用户进行了订单签收并不意味着终结,这只是一个新的开始,因为商品送达后可能会由于运输过程包装或商品有破损,商品本质量并非商品详情中所描述的那样等各种原因使用户进行退货或换货;还有一种场景是用户签收后发现有的商品漏发、少…...

低代码开发平台|生产管理-成本核算搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建生产管理-成本核算。1.2、应用场景计算主生产及子生产计划的工序成本、领料成本,统计出总的生产成本金额。2、设置方法2.1、表单搭建1)新建表单【商品信息】,字段设置如下;名称…...

Xshell 安装及使用方法
公网地址:47.XXX.XXX.229 私网地址:172.XXX.128.XXX 用户:root 密码:1234561,百度xshell,下载,安装Xshell 2,填写配置及使用方式 主机:47.XXX.XXX.229 用户:root 密码&a…...

【Axure教程】转盘抽奖原型模板
转盘抽奖是营销活动中很常用的一种方式,在线上我们也可以经常看到转盘抽奖的活动,所以今天作者就教大家在Axure中怎么制作一个转盘抽奖的原型模板。一、效果展示1、可以随机转动轮盘,轮盘停止时,指针对着的奖品高亮显示2、可以重复…...

量子比特大突破!原子薄材料成为“救世主”
(图片来源:网络)量子计算是一项极其复杂的技术,现阶段的一些挑战正严重阻碍着它的发展,尤其是量子比特的小型化和质量问题。IBM计划在2023年实现具有1121个超导量子比特的处理器。以目前的技术手段,要达到这…...
Swagger3 API接口文档规范课程(内含教学视频+源代码)
Swagger3 API接口文档规范课程(内含教学视频源代码) 教学视频源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87431932 目录Swagger3 API接口文档规范课程(内含教学视频源代码)教学视频源代…...

数据库的基本操作
查看数据库语法格式:SHOW {DATABASES | SCHEMAS}[LIKE pattern | WHERE expr]#查看全部数据库mysql> show databases; -------------------- | Database | -------------------- | information_schema | | mysql | | performance_schema …...
分享5个超好用的Vue.js库
开发人员最好的朋友和救星就是这些第三方库,无论是开发新手还是经验丰富的老手,我们都喜欢开源软件包。借助开源库加速Vue项目的开发进度是现代前端开发比较常见的方式,这几个 Vue.js库,建议尽早用上,加速你的项目开发…...

第四章.误差反向传播法—ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
第四章.误差反向传播法 4.2 ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现 1.ReLU层 1).公式 2).导数: 3).计算图: 4).实现: class ReLU:def __init__(self):self.mask None# 正向传播def forward(self, x):self.mask (x < 0) # 输入…...
Python-第二天 Python基础语法
Python-第二天 Python基础语法一、 字面量1.1 常用的值类型1.1.1 字符串(string)二、注释2.1 注释的作用2.2 注释的分类三、变量3.1 什么是变量3.2 变量的特征四、数据类型4.1 数据类型4.2 type()语句4.3 type()语句的使用方式4.4 变量有类型吗ÿ…...
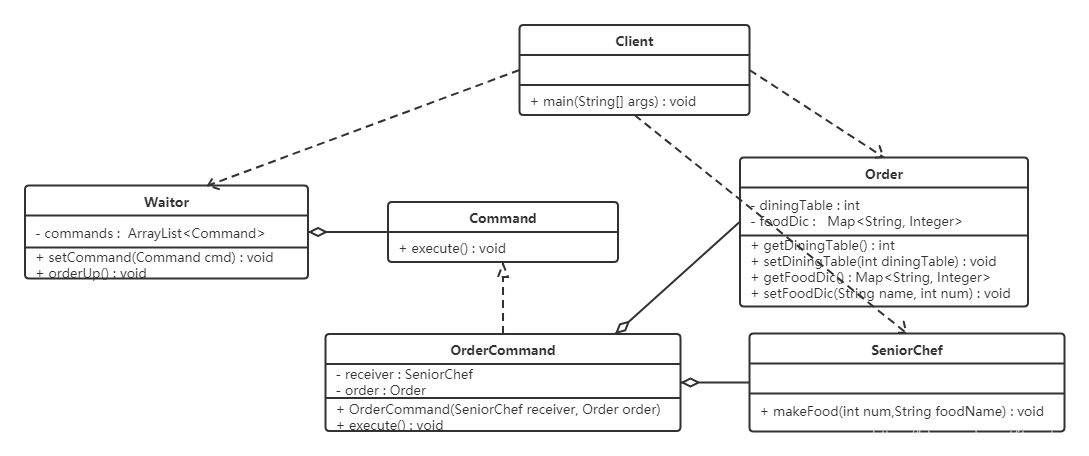
命令模式包含哪些主要角色?怎样实现命令?
命令模式包含以下主要角色:抽象命令类(Command)角色: 定义命令的接口,声明执行的方法。具体命令(Concrete Command)角色:具体的命令,实现命令接口;通常会持有…...

SpringCloud-Feign
Spring Cloud中集成Feign (只是笔记而已 其中有点命名啥的不对应,搜到了就划走吧) Feign--[feɪn]:Web 服务客户端,能够简化 HTTP 接口的调用。 没有Feign的之前服务提供者 package com.springcloudprovide.controller;import com.springclo…...

XCP实战系列介绍08-基于Vehicle Spy进行XCP测量的工程配置详解
本文框架 1.概述2. 工程配置步骤2.1 创建MEP工程2.1.1 添加A2L文件2.1.2 CAN收发ID配置2.2 MEP属性设置2.2.1 ECU属性设置2.2.2 MEP的Security设置2.3 DAQ设置2.3.1创建DAQ2.3.2 list中测量及标定量的添加和设置2.3.3 设置DAQ list中变量的event1.概述 在前面一篇文章《看了就…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
