2023/2/13总结
今天主要学习了哈夫曼树。
哈夫曼树
哈夫曼树是二叉树的一种,它是一种WPL最优二叉树。
叶子结点(也称叶节点):指的是自己下面不再连接有节点的节点(即末端),称为叶子节点(又称为终端结点)。
WPL是二叉树的带权路径长度,是指所有叶节点的路径长度乘以当前叶节点的权值之和,打一个比方:
下面有一个字符串,我们以字母出现次数作为权值,a所对应的权值4,我们需要构造一个二叉树,最优WPL的二叉树。
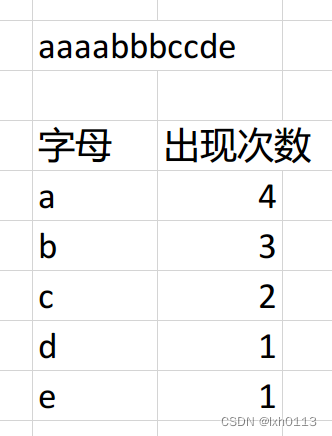
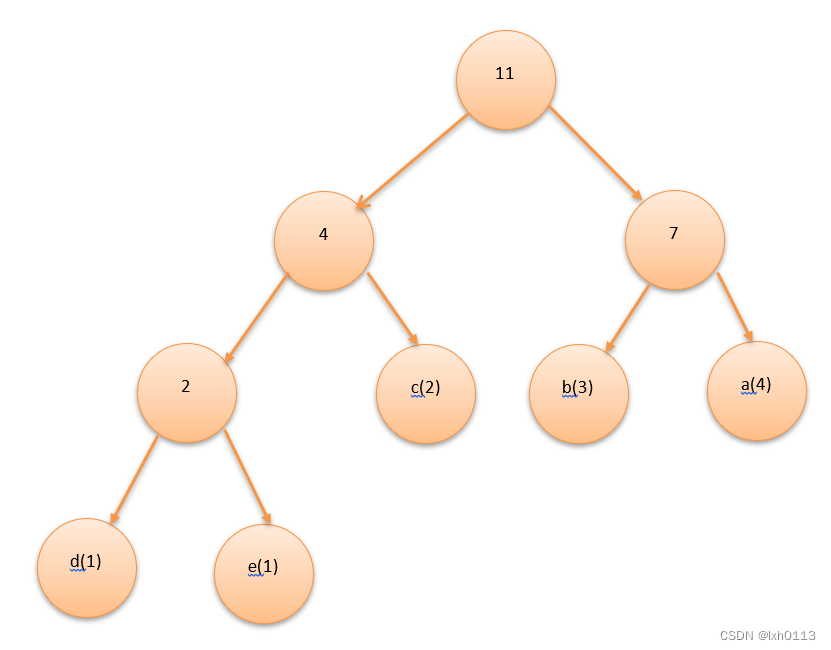
这是最优的哈夫曼树了,你再也找不到一个比这更优的了,那么它的WPL值为
1*3+1*3+2*2+3*2+4*2=24
还有一个更简洁的计算方法就是将图中的非叶结点值相加,11+4+7+2=24.
存储元素的结点为2*n-1,我们原来有5个结点,最后变成了9个结点
这很巧妙了,接下来讲解如何构建一个哈夫曼树。
在表中找俩个最小值作为结点的左右孩子
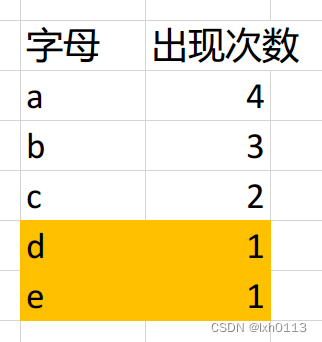
很明显是d e所代表的权值,新结点的权值为俩孩子的权值之和,即是2
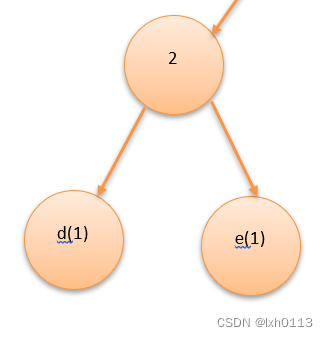
我们需要更新权值的数组,就是删除数组中c d的权值,把新节点的权值写入数组
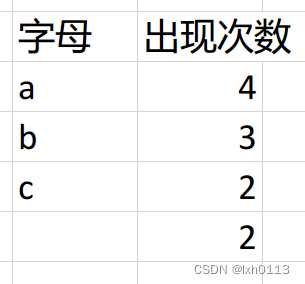
再继续找俩最小值,是c代表的2和另外一个没名字的结点,从下往上插入哦。
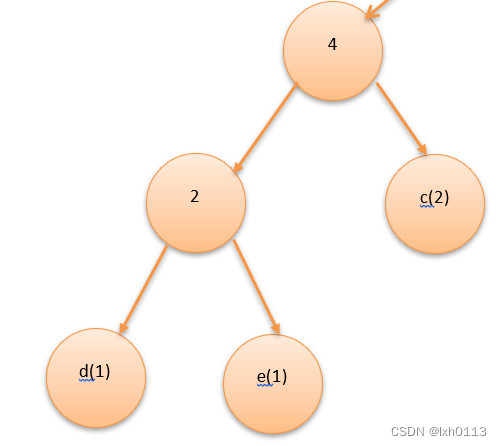
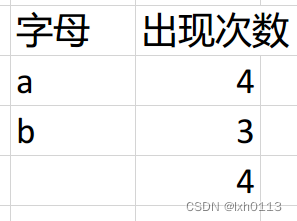
重复这些操作知道权值数组没有数值,最后就会变成开篇讲的那样子。
构建哈夫曼树,主要是为了满足哈夫曼编码。
哈夫曼编码是编码的一种,它是用来压缩文本的,主要压缩一段较长并且重复率较高的代码。
之所以那样子建立树,是为了将出现次数多的字符放在前面,出现次数少的字符放在后面,保证访问率的快慢。
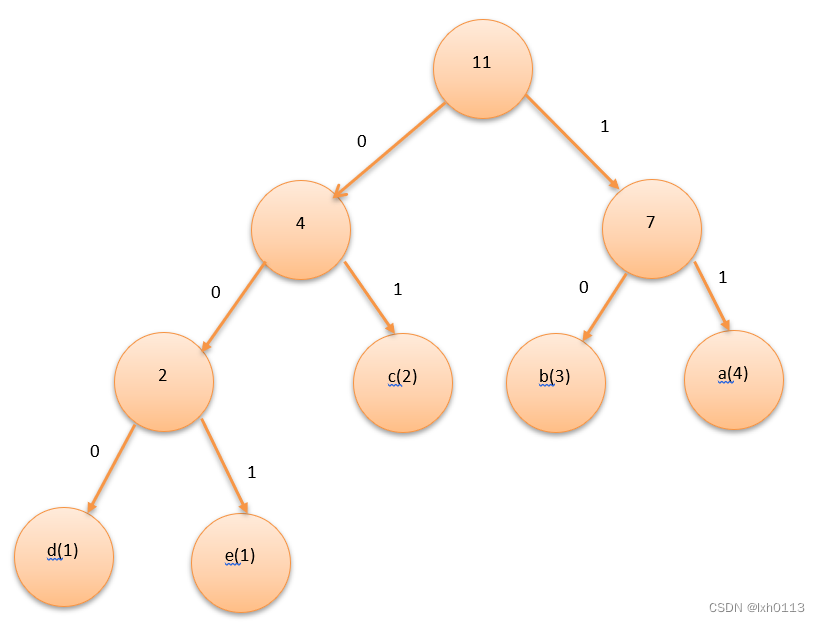
如上面所示将左边赋值为0,右边为1,我们可以发现一个特性,叶节点所构成的值,是不会有重复前缀的。(当然末尾俩个端点是会有一样的前缀,我们通常按照大小将其左右,左边是较小的,右边的较大的)
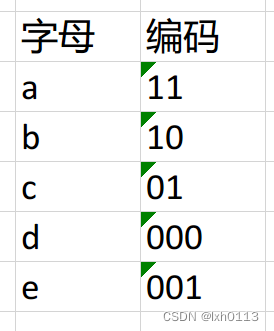

继而会变成上面那样子,我写的时候带了空格为了美观,实际存储时不带的,我们只需要根据哈夫曼树,按顺序找第一次出现的叶节点的编码,就可以凑成以上的字符串,(你可以自己试一试)。
哈夫曼编码是不等长编码。在一段长的重复率较高的文章特别适用。
相关文章:

2023/2/13总结
今天主要学习了哈夫曼树。 哈夫曼树 哈夫曼树是二叉树的一种,它是一种WPL最优二叉树。 叶子结点(也称叶节点):指的是自己下面不再连接有节点的节点(即末端),称为叶子节点(又称为终…...

webSock前端
1.什么是webSocket WebSocket是一种在单个TCP连接上进行全双工通信的协议。允许服务端主动向客户端推送数据。 2.如何使用webSocket WebSocket 构造函数WebSocket 对象作为一个构造函数,用于新建 WebSocket 实例。 代码如下: let ws = new WebSocket(网址); 2.websock事件: …...
)
AcWing 3956. 截断数组(每日一题)
AcWing 3956. 截断数组 题目描述 给定一个长度为 nnn 的数组 a1,a2,…,ana_1, a_2, …, a_na1,a2,…,an 。 现在,要将该数组从中间截断,得到三个非空子数组。 要求,三个子数组内各元素之和都相等。 请问,共有多少种不同…...

Android 一体机研发之修改系统设置————屏幕亮度
Android 一体机研发之修改系统设置————屏幕亮度 Android 一体机研发之修改系统设置————声音 Android 一体机研发之修改系统设置————自动锁屏 前言 最近工作略微有点儿空闲,抽空给大家总结一下:近期一直搞得一体机app研发,适用…...

C++通用算法
1.概述根据名字就知道如何使用相关算法,比如copy函数,就是复制的意思,它需要一个范围,以及要复制的位置copy(begin, end, container_begin);#include <iostream> #include<vector> #include<algorithm> #includ…...

Springboot停机方式
1. 介绍 简单的说,就是向应用进程发出停止指令之后,能保证正在执行的业务操作不受影响,直到操作运行完毕之后再停止服务。应用程序接收到停止指令之后,会进行如下操作: 1.停止接收新的访问请求 2.正在处理的请求&…...

Linux perf_event_open 简介
文章目录前言一、简介二、struct perf_event_attr2.1 type2.2 size2.3 config2.3.1 PERF_TYPE_HARDWARE2.3.2 PERF_TYPE_SOFTWARE2.3.3 PERF_TYPE_TRACEPOINT2.3.4 PERF_TYPE_HW_CACHE2.3.5 其他类型三、sample相关参数3.1 sample_period3.2 sample_freq3.3 sample_type四、其他…...

Java给定两组起止日期,求交集
/*** 判断2个时间段是否有重叠(交集)* param startDate1 时间段1开始时间戳* param endDate1 时间段1结束时间戳* param startDate2 时间段2开始时间戳* param endDate2 时间段2结束时间戳* param isStrict 是否严格重叠,true 严格࿰…...
数组的复制与二维数组的用法
今天学习的主要内容有 数组的复制 数组的复制 利用循环进行数组的复制 import java.util.Arrays; public class Main3 {public static void main(String[] args) {int []arr new int[]{1,2,3,4,5,6};int []arr1 new int[arr.length];for (int i 0; i < arr.length; i…...
)
JS判断两个table数据是否完全相等(判断两个数组对象是否完全相等)
需求 现有的table为tableA,有多个要做对比的table为一个数组 CompareArray 涉及到的问题 外层是数组,但是内部数据都是对象,对象属性名的排序不一样外层数组也涉及到 顺序不一样的问题 思路 对compareArray做长度筛选 filter 得到 同长度…...

关于小程序,你想知道的这些
近年来,各大平台纷纷上架小程序,迎来了小程序的爆发式增长。今天就来跟大家简单分享一下小程序基本的运行机制和安全机制。 小程序的由来 在小程序没有出来之前,最初微信WebView逐渐成为移动web重要入口,微信发布了一整套网页开…...

WuThreat身份安全云-TVD每日漏洞情报-2023-02-13
漏洞名称:THORSTEN PHPMYFAQ 跨站点脚本 漏洞级别:高危 漏洞编号:CVE-2023-0791 相关涉及:THORSTEN PHPMYFAQ 3.1.10 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-03506 漏洞名称:TENDA AC23 越界写入 漏洞级别:高危 漏洞编号:CVE-2023-078…...
【Linux】软件安装(三分钟教会你如何在linux下安装软件)
🔥🔥 欢迎来到小林的博客!! 🛰️博客主页:✈️小林爱敲代码 🛰️博客专栏:✈️Linux之路 🛰️社区:✈️进步学堂 目录&…...

Fluent Python 笔记 第 10 章 序列的修改、散列和切片
本章将以第 9 章定义的二维向量 Vector2d 类为基础,向前迈出一大步,定义表示多维向量的 Vector 类。这个类的行为与 Python 中标准的不可变扁平序列一样。 10.3 协议和鸭子类型 在 Python 中创建功能完善的序列类型无需使用继承,只需实现符…...
在中国程序员工作是青春饭吗?
上个月公司告诉我毕业了。 我打开boss直聘,一溜溜的外包公司和我打招呼。 我寻思我说不定啥时候就离开深圳了,外包不外包也无所谓钱到位就行。(大公司学历不够格也进不去) 结果华为、平安的外包告诉我,不好意思呀&a…...

Linux tcpdump
tcpdump - 转储网络上的数据流 是不是感觉很懵?全方位描述tcpdump: 通俗:tcpdump是一个抓包工具,用于抓取网络中传输的数据包形象:tcpdump如同国家海关,凡是入境和出境的货物,海关都要抽样检查࿰…...
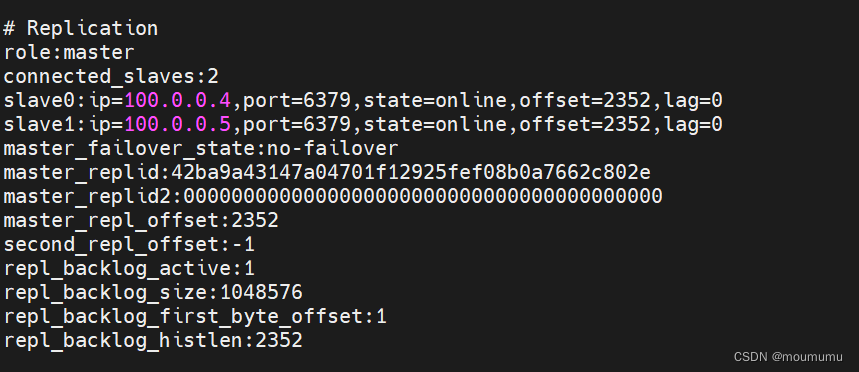
redis知识汇总(部署、高可用、集群)
文章目录一、redis知识汇总什么是redisredis的优缺点:为什么要用redis做缓存redis为什么这么快什么是持久化redis持久化机制是什么?各自优缺点?AOF和RDB怎么选择redis持久化数据和缓存怎么做扩容什么是事务redis事务的概念ACID概念主从复制re…...

【手写 Vuex 源码】第十篇 - Vuex 命名空间的实现
一,前言 上一篇,主要介绍了 Vuex 响应式数据和缓存的实现,主要涉及以下几个点: Vuex 的响应式实现原理;响应式核心方法 resetStoreVM;commit 和 dispatch 的处理; 本篇,继续介绍 …...
面试腾讯测试岗后感想,真的很后悔这5年一直都干的是基础测试....
前两天,我的一个朋友去大厂面试,跟我聊天时说:输的很彻底… 我问她:什么情况?她说:很后悔这5年来一直都干的是功能测试… 相信许多测试人也跟我朋友一样,从事了软件测试很多年,却依…...
)
知识图谱 方法、实践与应用 王昊奋 读书笔记(下)
最近读了这本书,在思路上很有启发,对知识图谱有了初步的认识,以下是原书后半部分的内容,可以购买实体书获取更多内容。 知识图谱推理 结合已有规则,推出新的事实,例如持有股份就能控制一家公司࿰…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
