【python--networkx】函数说明+代码讲解
【Python–NetworkX】函数说明+代码讲解
文章目录
- 【Python--NetworkX】函数说明+代码讲解
- 1. 介绍
- 1.1 前言
- 1.2 图的类型(Graph Types)
- 1.3 常用方法
- 2. 代码示例
1. 介绍
1.1 前言
NetworkX是复杂网络研究领域中的常用Python包。
1.2 图的类型(Graph Types)
允许以可哈希的object作为节点,任何Python object作为边属性。
如何选择使用哪种图:
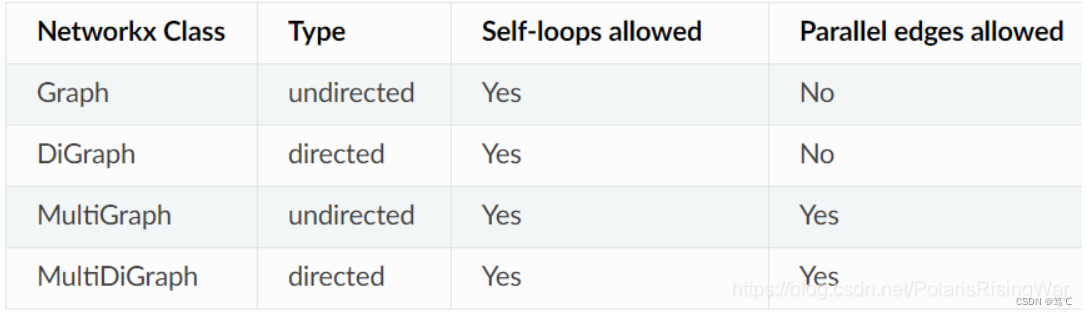
这里解释一下什么是平行边:连接一对顶点的两条边叫做平行边,即,无向图中,两个顶点间有多条边,他们叫做平行边,打个比方,北京和上海直接可以 是公路、铁路、飞机,那么他们互为平行边。
1.3 常用方法
- 创建一个空的图
1)无向图:G = nx.Graph()
2)有向图:DG = nx.DiGraph() - 将有向图转换为无向图:G = nx.Graph(DG)
- 图是否有向:G.is_directed() 返回布尔值
- 添加节点
1)直接添加一个节点(任何object都可以作为节点,包括另一个图)G.add_node(1)、G.add_node(DG)
2)从任何容器加点:a list, dict, set or even the lines from a file or the nodes from another graph…;G.add_nodes_from() 或 nx.path_graph() - 添加边
1)添加一条边 G.add_edge(u, v)
2)添加一个边的列表 G.add_edges_from([(1, 2), (1, 3)])
3)添加一个边的collection G.add_edges_from(H.edges)
4)如果添加的边的点不存在于图中,会自动添上相应节点而不报错 - 属性attribute
1)图的节点/边/图都可以在关联的attribute字典中以键值对key/value形式存储attribute(key一定要是可哈希的)
2)默认情况下属性字典是空的
3)可以通过add_edge() add_node() 方法或直接操作分别名为graph edges nodes的属性字典来进行操作
2. 代码示例
import networkx as nx
import numpy as np #定义图的节点和边
nodes=['0','1','2','3','4','5','a','b','c']
edges=[('0','0',1),('0','1',1),('0','5',1),('0','5',2),('1','2',3),('1','4',5),('2','1',7),('2','4',6),('a','b',0.5),('b','c',0.5),('c','a',0.5)] plt.subplots(1,2,figsize=(10,3)) #定义一个无向图和有向图
G1 = nx.Graph()
G1.add_nodes_from(nodes)
G1.add_weighted_edges_from(edges) G2 = nx.DiGraph()
G2.add_nodes_from(nodes)
G2.add_weighted_edges_from(edges) pos1=nx.circular_layout(G1)
pos2=nx.circular_layout(G2) #画出无向图和有向图
plt.subplot(121)
nx.draw(G1,pos1, with_labels=True, font_weight='bold')
plt.title('无向图',fontproperties=myfont)
plt.axis('on')
plt.xticks([])
plt.yticks([]) plt.subplot(122)
nx.draw(G2,pos2, with_labels=True, font_weight='bold')
plt.title('有向图',fontproperties=myfont)
plt.axis('on')
plt.xticks([])
plt.yticks([]) plt.show() #控制numpy输出小数位数
np.set_printoptions(precision=3) #邻接矩阵
A = nx.adjacency_matrix(G1)
print('邻接矩阵:\n',A.todense())
邻接矩阵: [[0. 0. 0. 0. 5. 0. 0. 0. 6. ] [0. 0. 0. 2. 0. 0. 0. 0. 0. ] [0. 0. 0. 0. 0. 0.5 0.5 0. 0. ] [0. 2. 0. 1. 1. 0. 0. 0. 0. ] [5. 0. 0. 1. 0. 0. 0. 0. 7. ] [0. 0. 0.5 0. 0. 0. 0.5 0. 0. ] [0. 0. 0.5 0. 0. 0.5 0. 0. 0. ] [0. 0. 0. 0. 0. 0. 0. 0. 0. ] [6. 0. 0. 0. 7. 0. 0. 0. 0. ]] #关联矩阵
I = nx.incidence_matrix(G1)
print('\n关联矩阵:\n',I.todense())
关联矩阵: [[1. 1. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 1. 1. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 1. 0. 0. 0.] [0. 1. 0. 0. 0. 1. 0. 1. 0.] [0. 0. 0. 1. 0. 0. 0. 0. 1.] [0. 0. 0. 0. 1. 0. 0. 0. 1.] [0. 0. 0. 0. 0. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 1. 0.]] #拉普拉斯矩阵
L=nx.laplacian_matrix(G1)
print('\n拉普拉斯矩阵:\n',L.todense())
拉普拉斯矩阵: [[11. 0. 0. 0. -5. 0. 0. 0. -6. ] [ 0. 2. 0. -2. 0. 0. 0. 0. 0. ] [ 0. 0. 1. 0. 0. -0.5 -0.5 0. 0. ] [ 0. -2. 0. 3. -1. 0. 0. 0. 0. ] [-5. 0. 0. -1. 13. 0. 0. 0. -7. ] [ 0. 0. -0.5 0. 0. 1. -0.5 0. 0. ] [ 0. 0. -0.5 0. 0. -0.5 1. 0. 0. ] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [-6. 0. 0. 0. -7. 0. 0. 0. 13. ]] #标准化的拉普拉斯矩阵
NL=nx.normalized_laplacian_matrix(G1)
print('标准化的拉普拉斯矩阵:\n',NL.todense())
标准化的拉普拉斯矩阵: [[ 1. 0. 0. 0. -0.418 0. 0. 0. -0.502] [ 0. 1. 0. -0.707 0. 0. 0. 0. 0. ] [ 0. 0. 1. 0. 0. -0.5 -0.5 0. 0. ] [ 0. -0.707 0. 0.75 -0.139 0. 0. 0. 0. ] [-0.418 0. 0. -0.139 1. 0. 0. 0. -0.538] [ 0. 0. -0.5 0. 0. 1. -0.5 0. 0. ] [ 0. 0. -0.5 0. 0. -0.5 1. 0. 0. ] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. ] [-0.502 0. 0. 0. -0.538 0. 0. 0. 1. ]] #有向图拉普拉斯矩阵
DL=nx.directed_laplacian_matrix(G2)
print('\n有向拉普拉斯矩阵:\n',DL)
有向拉普拉斯矩阵: [[ 0.889 -0.117 -0.029 -0.087 -0.319 -0.029 -0.029 -0.129 -0.242] [-0.117 0.889 -0.026 -0.278 -0.051 -0.026 -0.026 -0.114 -0.056] [-0.029 -0.026 0.994 -0.012 -0.009 -0.481 -0.481 -0.025 -0.01 ] [-0.087 -0.278 -0.012 0.757 -0.097 -0.012 -0.012 -0.052 -0.006] [-0.319 -0.051 -0.009 -0.097 0.994 -0.009 -0.009 -0.041 -0.434] [-0.029 -0.026 -0.481 -0.012 -0.009 0.994 -0.481 -0.025 -0.01 ] [-0.029 -0.026 -0.481 -0.012 -0.009 -0.481 0.994 -0.025 -0.01 ] [-0.129 -0.114 -0.025 -0.052 -0.041 -0.025 -0.025 0.889 -0.045] [-0.242 -0.056 -0.01 -0.006 -0.434 -0.01 -0.01 -0.045 0.994]] #拉普拉斯算子的特征值
LS=nx.laplacian_spectrum(G1)
print('\n拉普拉斯算子的特征值:\n',LS)
拉普拉斯算子的特征值: [-1.436e-15 0.000e+00 4.610e-16 7.000e-01 1.500e+00 1.500e+00 4.576e+00 1.660e+01 2.013e+01] #邻接矩阵的特征值
AS=nx.adjacency_spectrum(G1)
print('邻接矩阵的特征值:\n',AS)
邻接矩阵的特征值: [12.068+0.000e+00j 2.588+0.000e+00j -7.219+0.000e+00j -4.925+0.000e+00j -1.513+0.000e+00j 1. +0.000e+00j -0.5 +2.393e-17j -0.5 -2.393e-17j0. +0.000e+00j]#无向图的代数连通性
AC=nx.algebraic_connectivity(G1)
print('无向图的代数连通性:\n',AC)
无向图的代数连通性: 0.0 #图的光谱排序
SO=nx.spectral_ordering(G1)
print('图的光谱排序:\n',SO)
图的光谱排序: ['4', '2', '1', '0', '5', 'b', 'c', 'a', '3'] 相关文章:

【python--networkx】函数说明+代码讲解
【Python–NetworkX】函数说明代码讲解 文章目录【Python--NetworkX】函数说明代码讲解1. 介绍1.1 前言1.2 图的类型(Graph Types)1.3 常用方法2. 代码示例1. 介绍 1.1 前言 NetworkX是复杂网络研究领域中的常用Python包。 1.2 图的类型(G…...
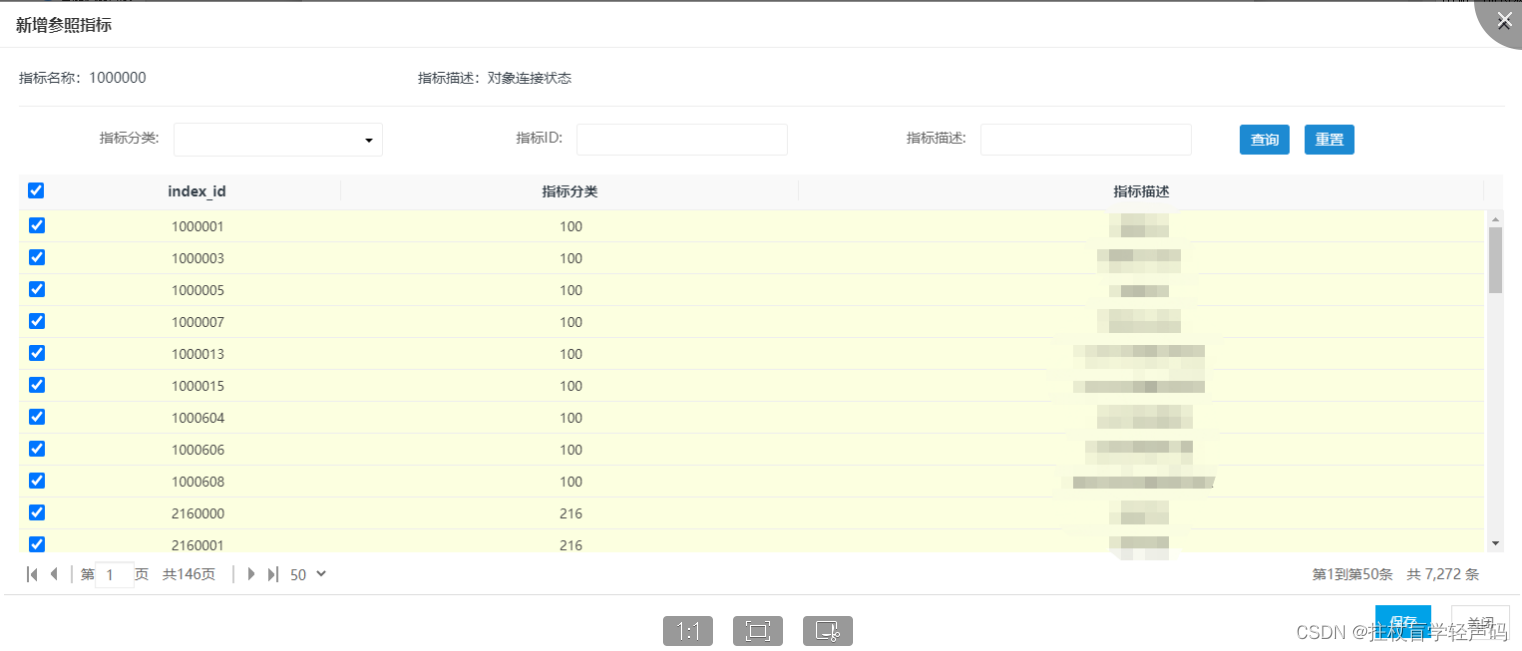
【Jqgrid分页勾选保存】三步实现表格分页勾选(取消勾选)保存(附源码)
目录1、创建临时存储数组,初始化赋值2、单行选中与取消,调整数组3、全选与取消全选,调整数组4、输出数组保存5、片尾彩蛋【写在前面】表格可以说是在我们的web页面中是最常见的,之前我们介绍过layui表格翻页勾选的实现过程&#x…...
Appium移动自动化测试——app控件获取之uiautomatorviewer
下载手机YY http://yydl.duowan.com/mobile/yymobile_client-android/5.4.2/yymobile_client-5.4.2-881.apk 若链接失效,请自行百度 新建maven空白工程 前置条件:安装eclipse,及其maven插件,请自行百度 新建的工程如下…...
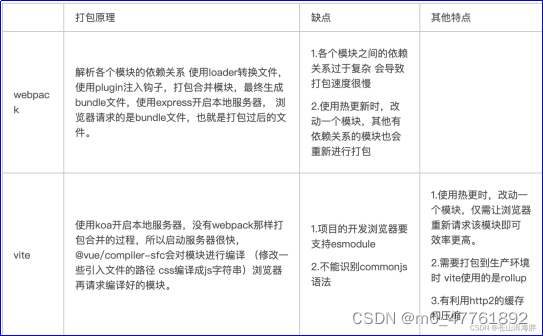
webpack、vite、vue-cli、create-vue 的区别
webpack、vite、vue-cli、create-vue 的区别 首先说结论 Rollup更适合打包库,webpack更适合打包项目应用,vite基于rollup实现了热更新也适合打包项目。 功能工具工具脚手架vue-clicreate-vue构建项目vite打包代码webpackrollup 脚手架:用于初始化&#…...
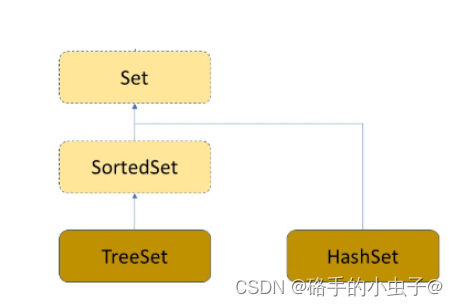
数据结构——TreeMap、TreeSet与HashMap、HashSet
目录 一、Map 1、定义 2、常用方法 3、注意 二、TreeMap 三、HashMap 1、定义 2、冲突定义 3、冲突避免方法——哈希函数设计 (1)、直接定制法(常用) (2)、除留余数法(常用) (3)、平方取中法 &…...
Spring Boot学习篇(十三)
Spring Boot学习篇(十三) shiro安全框架使用篇(五) 1 准备工作 1.1 在SysUserMapper.xml中书写自定义标签 <select id"findRoles" resultType"string">select name from sys_role where id (select roleid from sys_user_role where userid (S…...

微软Bing的AI人工只能对话体验名额申请教程
微软Bing 免费体验名额申请教程流程ChatGPT这东西可太过火了。国外国内,圈里圈外都是人声鼎沸。微软,谷歌,百度这些大佬纷纷出手。连看个同花顺都有GPT概念了,搞技术,做生意的看来都盯上了 流程 下面就讲一下如何申…...
怎么打造WhatsApp Team?SaleSmartly(ss客服)告诉你
关键词:WhatsApp Team SaleSmartly(ss客服) 您是否正在寻找一种让您的团队能够在 WhatsApp协作消息传递的解决方案?拥有了 WhatsApp Team,不仅效率提升,还可以在智能聊天工具中比如SaleSmartly(ss客服&…...

IPV4地址的原理和配置
第三章:IP地址的配置 IPv4(Internet Protocol Version 4)协议族是TCP/IP协议族中最为核心的协议族。它工作在TCP/IP协议栈的网络层,该层与OSI参考模型的网络层相对应。网络层提供了无连接数据传输服务,即网络在发送分…...
软件测试面试准备——(一)Selenium(1)基础问题及自动化测试
滴滴面试:1. 自己负责哪部分功能?农餐对接系统分为了两大子系统,一个是个人订餐系统,二是餐馆、个人与农产品供应商进行农产品交易系统。我主要负责组织测试人员对该系统进行测试。我们测试分为两个阶段:一、功能测试阶…...

AcWing 1230.K倍区间
AcWing 1230. K倍区间 题目描述 给定一个长度为 NNN 的数列,A1,A2,…ANA_1, A_2, … A_NA1,A2,…AN ,如果其中一段连续的子序列 Ai,Ai1,…AjA_i, A_{i1}, … A_jAi,Ai1,…Aj 之和是 KKK 的倍数,我们就称这个区间 [i,j][i,j][i,…...
kubernetes集群部署springcloud项目【AL】【未写完】
kubernetes集群部署springcloud项目【AL】 (先手工做,非自动化) #环境: 192.168.73.138 master 192.168.73.139 node1 192.168.73.140 node2 192.168.73.137 harbor、mysqlgit clone https://github.com/lizhenliang/simple-…...
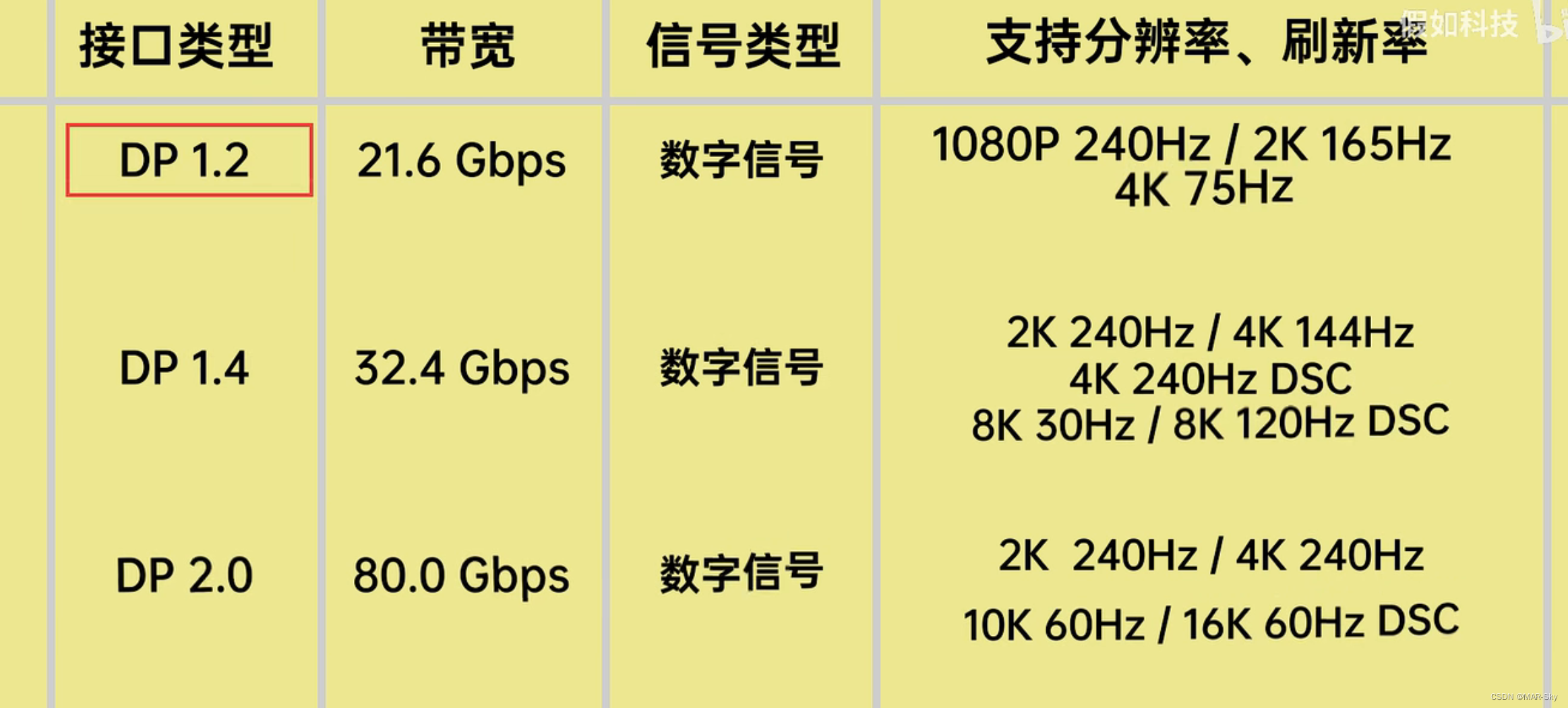
各种音频接口比较
时间 参考:https://www.bilibili.com/video/BV1SL4y1q7GZ/?spm_id_from333.337.search-card.all.click&vd_source00bd76f9d6dc090461cddd9f0deb2d51, https://blog.csdn.net/weixin_43794311/article/details/128941346 接口名字时间公司支持格式…...
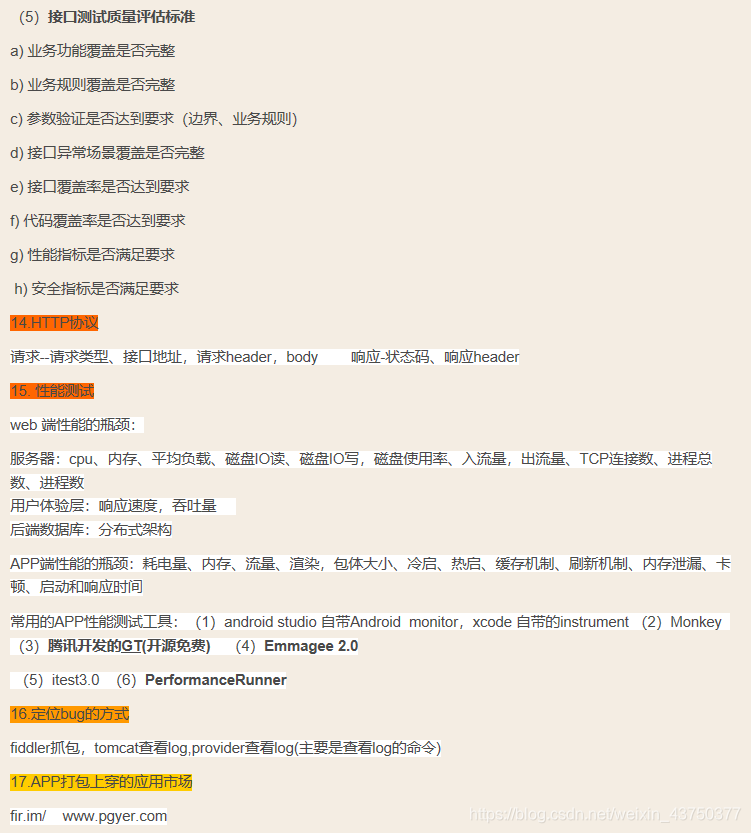
软件测试面试理论(超详细)
【面试理论知识】1、你的测试职业发展是什么? 测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前3年积累测试经验,按如何做好测试工程师的要点去要求自己…...
)
c++学习笔记-二进制文件操作(哔站-黑马程序员c++教学视频)
一、基本概念 以二进制的方式对文件进行读写操作 打开方式指定为 ios::binary 优点:可以写入自己定义的数据类型 1、写文件 二进制方式写文件:流对象调用成员write 函数原型:ostream& write(const char * buffer,int len);参数解释…...

内网渗透(二十三)之Windows协议认证和密码抓取-Mimikatz介绍和各种模块使用方法
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Nginx if的使用教程
if指令该指令用来支持条件判断,并根据条件判断结果选择不同的Nginx配置。语法if (condition){...}默认值—位置server、locationcondition为判定条件,可以支持以下写法:1. 变量名。如果变量名对应的值为空字符串或"0",i…...
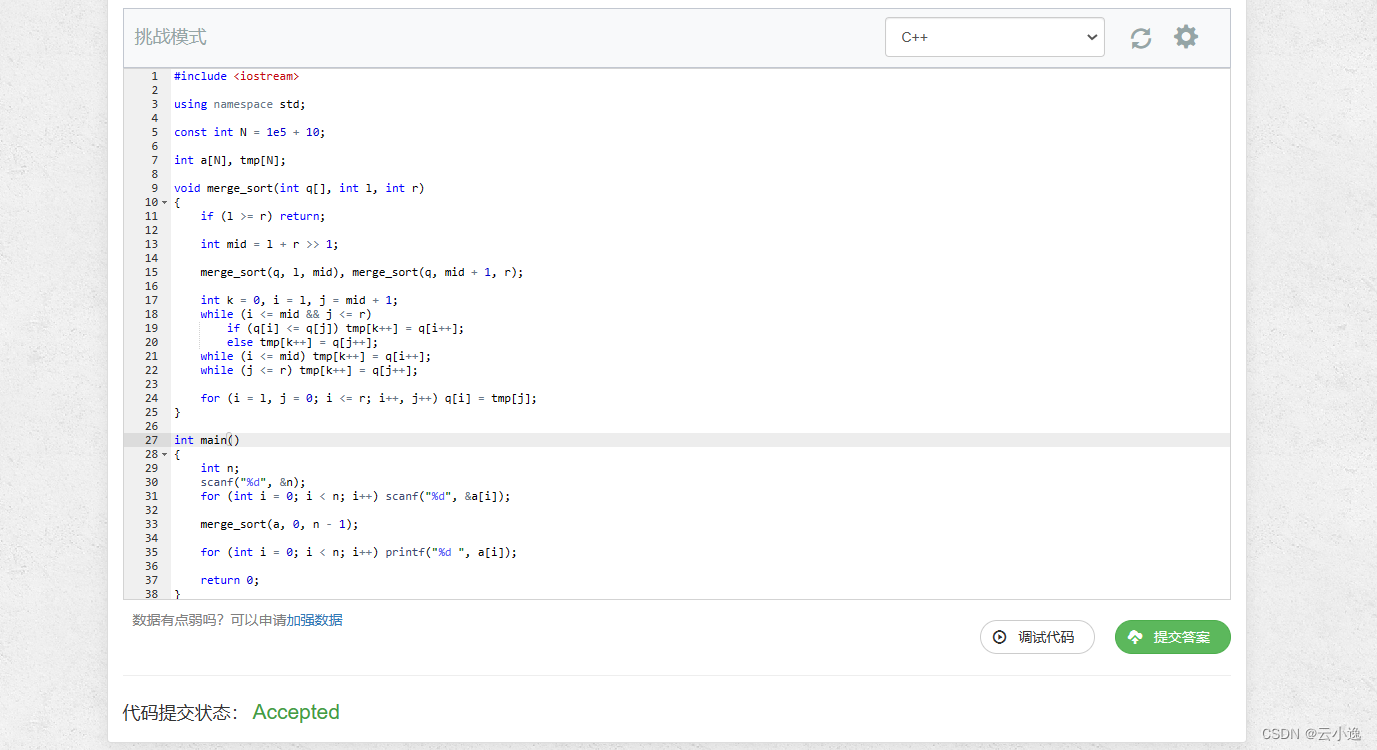
备考蓝桥杯【快速排序和归并排序】
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Taro使用微信OCR插件无法调用onSuccess回调问题
Taro使用微信插件无法调用onSuccess回调问题小程序后台添加插件在开放社区购买相应的套餐详细步骤1.在app.config.js中添加如下代码2.在页面的page.config.js添加插件3.使用ocr-navigator识别身份证小程序后台添加插件 在开放社区购买相应的套餐 购买地址 详细步骤 1.在app.…...
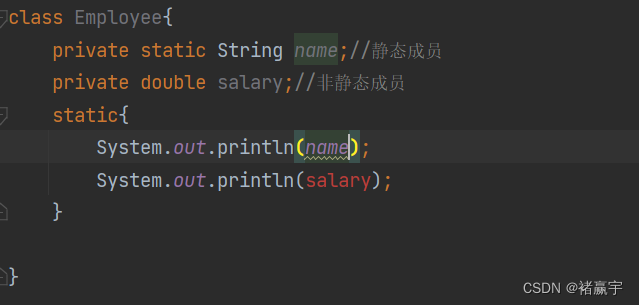
【Java】代码块的细节你搞懂了吗(基础知识七)
希望像唠嗑一样,one step one futher。 目录 (1)代码块的应用场景 (2)代码块的细节 1.static 代码块只加载一次 2.当调用类的静态成员时,类会加载 3. 使用类的静态成员时,static代码块会被执…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
