深度学习_L2正则化
文章目录
- 参考博客
- 正则化介绍
- 正则化的实现
参考博客
深入理解L1、L2正则化
PyTorch 实现L2正则化以及Dropout的操作
正则化介绍
正则化(Regularization)是机器学习中一种常用的技术,其主要目的是控制模型复杂度,减小过拟合。最基本的正则化方法是在原目标(代价)函数 中添加惩罚项,对复杂度高的模型进行“惩罚”。其数学表达形式为:
Jˇ(w;X,y)=J(w;X,y)+αΩ(w)\check{J}(w; X, y)=J(w; X, y) + \alpha\Omega(w)Jˇ(w;X,y)=J(w;X,y)+αΩ(w)
式中X,yX, yX,y为训练样本和相应标签, www为权重系数向量; J()J()J()为目标函数, Ω(w)\Omega(w)Ω(w)即为惩罚项, 可理解为模型"规模"的某种度量; 参数α\alphaα控制正则化的强弱. 不同的Ω\OmegaΩ函数对权重w的最优解有不同的偏好, 因而会产生不同的正则化效果. 最常用的Ω\OmegaΩ函数有两种, 即l1l_1l1范数与l2l_2l2范数, 相应称之为l1l_1l1正则化和l2l_2l2正则化.此时有:
l1:Ω(w)=∣∣w∣∣1=∑i∣wi∣l_1: \Omega(w)=||w||_1=\sum_i|w_i|l1:Ω(w)=∣∣w∣∣1=∑i∣wi∣
l2:Ω(w)=∣∣w∣∣2=∑iwi2l_2: \Omega(w)=||w||_2=\sqrt{\sum_iw_i^2}l2:Ω(w)=∣∣w∣∣2=∑iwi2
正则化的实现
在Pytorch中正则化的实现只需要一行代码, 如下:
optimizer = torch.optim.SGD(model.parameters(), \
lr=config.learning_rate, momentum=0.9, weight_decay=0.000001)
在这个函数调用中weight_decay=0.001weight\_decay=0.001weight_decay=0.001就是L2范数.
相关文章:

深度学习_L2正则化
文章目录参考博客正则化介绍正则化的实现参考博客 深入理解L1、L2正则化 PyTorch 实现L2正则化以及Dropout的操作 正则化介绍 正则化(Regularization)是机器学习中一种常用的技术,其主要目的是控制模型复杂度,减小过拟合。最基…...
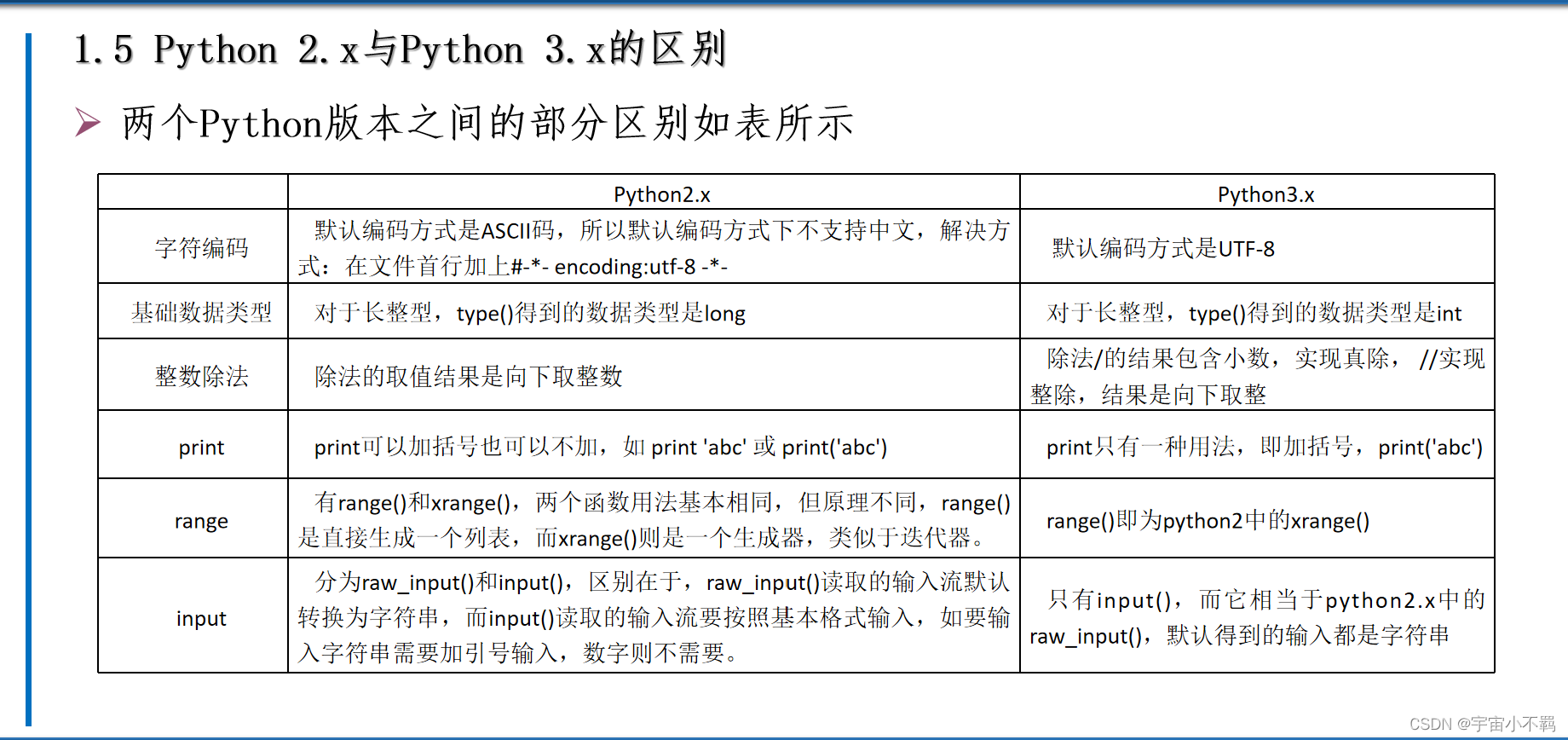
第一章 认识Python
本章目录 一、初识Python 二、Python环境安装 三、Python代码的执行 四、Python集成开发环境 五、Python2.x与Python3.x的区别 六、本章小结 Python代码的编辑和运行方式主要分为两种:交互模式和脚本模式。 在交互模式下, 用户输入Python代码并按…...

复习0206
目录 一、访问修饰符 一、权限范围 二、注意事项 二、封装(面向对象的三大特征之一) 一、封装的好处 二、封装的实现步骤 三、和构造器结合 四、练习题中的细节 一、访问修饰符 一、权限范围 访问修饰符用于控制方法和属性(成员变量…...

小红书如何查看笔记
小红书如何查看笔记 在小红书上找关键词的 6 大方法进阶版想要查找品类词、行业词、产品词、长尾词的小伙伴看过来,这一次我们就来给大家升级了 6 种找关键词的方法,也是我们的进阶版。 第一种,下拉框查找。我们只需要在小红书 AP 输入主要的…...
linux001之linux系统部署安装
注意:本次安装讲解以乌班图(Ubuntu) 虚拟机来说明讲解,既然学习linux,就无需用图形界面了,直接用服务器版本 1. 下载乌班图 网址:https://www.ubuntu.org.cn/download/server 然后就可以看到右下角有下载提示ÿ…...
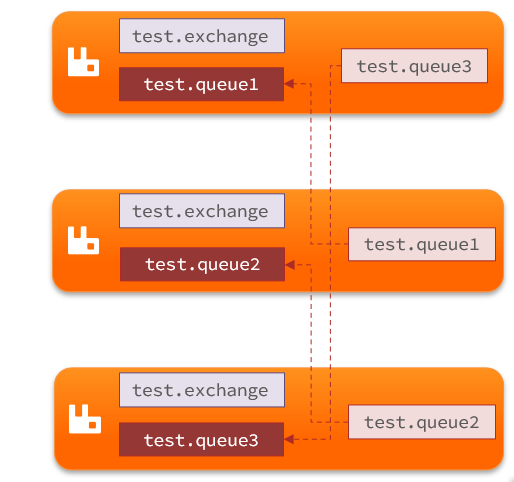
服务异步通信 RabbitMQ-高级篇
服务异步通信RabbitMQ-高级篇服务异步通信RabbitMQ-高级篇1.消息可靠性1.1.生产者消息确认1.1.1.修改配置1.1.2.定义Return回调1.1.3.定义ConfirmCallback1.2.消息持久化1.2.1.交换机持久化1.2.2.队列持久化1.2.3.消息持久化1.3.消费者消息确认1.3.1.演示none模式1.3.2.演示aut…...
【PR】零基础快速入门教程
【PR】零基础快速入门教程PR(Premiere)能做什么?PR欢迎界面及新建项目工作区及窗口说明导入文件建立序列视频剪辑添加字幕导出视频使用软件:Premiere2020新年卷起来,写文章已近不能满足与我了,我要向着更前…...
)
Matlab 点云迭代加权最小二乘法拟合平面(抑制噪声)
不要虚掷你的黄金时代,不要去倾听枯燥乏味的东西,不要设法挽留无望的失败,不要把你的生命献给无知、平庸和低俗。这些都是我们时代病态的目标,虚假的理想。 ----王尔德 文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 受到之前博客的启发(Matlab 点云最小二乘…...

2023 软件测试行业内卷动荡,红利期过去后,何去何从?
前段时间席卷全互联网行业的内卷现象,想必有不少人都深陷其中。其实刚开始测试行业人才往往供不应求,而在发展了十几年后,很多人涌入这个行业开始面对存量竞争。红利期过去了,只剩内部争夺。 即便如此,测试行业仍有许…...

【王道数据结构】第六章(下) | 图的应用
目录 一、最小生成树 二、最短路径 三、有向⽆环图描述表达式 四、拓扑排序 五、关键路径 一、最小生成树 1、最小生成树的概念 对于一个带权连通无向图G (V,E),生成树不,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所…...
)
Leetcode:518. 零钱兑换 II(C++)
目录 518. 零钱兑换 II 问题描述: 实现代码与解析: 动态规划(完全背包): 原理思路: 377. 组合总和 Ⅳ 问题描述: 实现代码与解析: 动态规划(完全背包࿰…...

Java中类是什么
类(class)是构造对象的模板或蓝图。 我们可以将类想象成制作小甜饼的模具,将对象想象为小甜饼。由类构造(construct)对象的过程称为创建类的实例(instance)。 正如前面所看到的,用Java 编写的所有代码都位于某个类里面。 标准 Java 库提供了几千个类&a…...
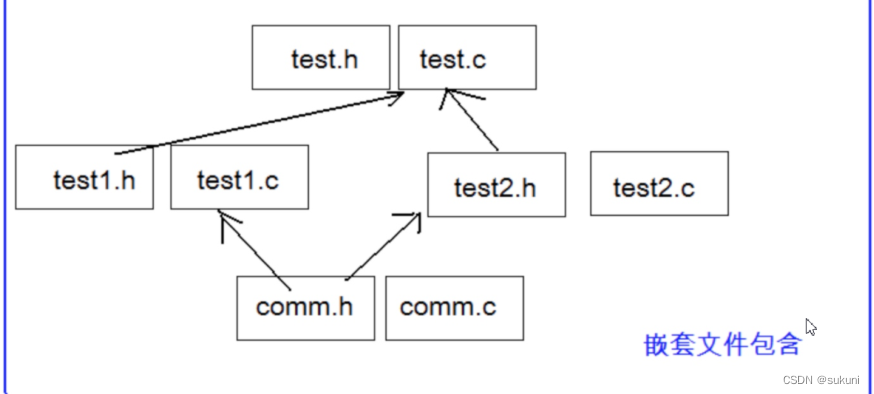
C进阶:预处理
🤖本篇文章主要讲解预处理的知识,即使你是小白也可以看的懂,若你对预处理有所不解,确定不来看看吗?😿 目录 一.代码运行是的两种环境 二.翻译环境 三.预定义符号 四.#define 1.define 定义宏 2.带有…...
侯捷C++系统工程师
前言我相信对于每一个学习C的同学和从业者来说,台湾著名学者侯捷老师的C系列都是不可错过的好视频。侯捷老师在网上已有五门课,分别是:C面向对象开发、STL标准库与泛型编程、C新标准C1&14、C内存管理机制以及C Startup揭秘讲师介绍侯捷老…...
ReentrantReadWriteLock、StampedLock
ReentrantLock、ReentrantReadWriteLock、StampedLock 读写锁 一个资源可以被多个读线程访问,或者被一个写线程访问,但是不能同时存在读写线程。 小口诀:读写互斥,读读共享 锁的演变 无锁-----> 独占锁----->读写锁---…...

Mysql中的事务、锁、日志详解
一、事务 1.事务特性及保证事务特性的原理 原子性:当前事务的操作要么全部成功,要么全部失败。原子性由undo log实现,undo log记录了每次操作之前的数据版本,如果某一操作失败,可以根据undo log回滚到最初状态。一致…...

k8s笔记24--安装metrics-server及错误处理
k8s笔记24--安装metrics-server及错误处理1 介绍2 安装3 常见错误第一次错误 持续 Failed probe第二次错误 bad status code "403 Forbidden"4 说明1 介绍 最近一个同事在老版本的 k8s 上安装metrics-server,pod一直处于running 非就绪状态,经…...
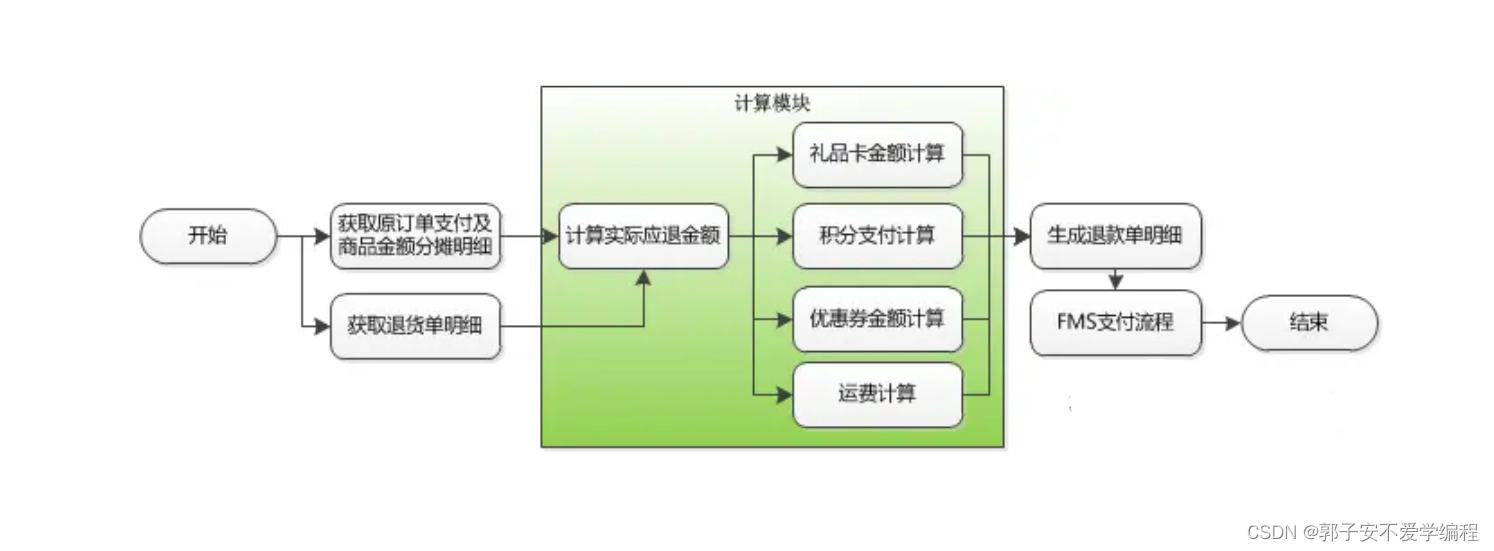
【电商】订单系统--售后的简易流程与系统关系
用户进行了订单签收并不意味着终结,这只是一个新的开始,因为商品送达后可能会由于运输过程包装或商品有破损,商品本质量并非商品详情中所描述的那样等各种原因使用户进行退货或换货;还有一种场景是用户签收后发现有的商品漏发、少…...

低代码开发平台|生产管理-成本核算搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建生产管理-成本核算。1.2、应用场景计算主生产及子生产计划的工序成本、领料成本,统计出总的生产成本金额。2、设置方法2.1、表单搭建1)新建表单【商品信息】,字段设置如下;名称…...

Xshell 安装及使用方法
公网地址:47.XXX.XXX.229 私网地址:172.XXX.128.XXX 用户:root 密码:1234561,百度xshell,下载,安装Xshell 2,填写配置及使用方式 主机:47.XXX.XXX.229 用户:root 密码&a…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
