方向导数与梯度下降
文章目录
- 方向角与方向余弦
- 方向角
- 方向余弦
- 方向导数
- 定义
- 性质
- 梯度下降
梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
方向角与方向余弦
方向角
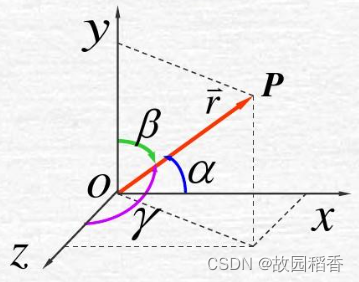
向量(或有向直线)与坐标轴正向或基向量的交角称为向量的方向角。定义域为[0,π][0,\pi][0,π]。
方向余弦
{cosα=x∣r∣cosβ=y∣r∣cosγ=z∣r∣\begin{cases} \cos\alpha = \frac{x}{|r|}\\ \cos\beta = \frac{y}{|r|}\\ \cos\gamma = \frac{z}{|r|} \end{cases}⎩⎨⎧cosα=∣r∣xcosβ=∣r∣ycosγ=∣r∣z
且有cos2α+cos2β+cos2γ=1\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1cos2α+cos2β+cos2γ=1
方向导数
定义
给定标量函数f(x,y,z)f(x,y,z)f(x,y,z),和任意向量l⃗\vec{l}l,该向量与三个坐标轴的夹角分别为α\alphaα、β\betaβ、γ\gammaγ,从定义域中一定P0(x,y,z)P_0(x,y,z)P0(x,y,z)出发,沿着向量l⃗\vec{l}l方向移动距离Δs\Delta sΔs,到达点P1(x+Δscosα,y+Δscosβ,z+Δscosγ)P_1(x+\Delta s \cos\alpha,y+\Delta s \cos\beta,z+\Delta s \cos\gamma)P1(x+Δscosα,y+Δscosβ,z+Δscosγ),定义方向导数:
dfdl⃗=limΔs→0f(x+Δscosα,y+Δscosβ,z+Δscosγ)−f(x,y,z)Δs\frac{df}{d\vec{l}}=\lim_{\Delta s \to 0}\frac{f(x+\Delta s \cos\alpha,y+\Delta s \cos\beta,z+\Delta s \cos\gamma)-f(x,y,z)}{\Delta s}dldf=limΔs→0Δsf(x+Δscosα,y+Δscosβ,z+Δscosγ)−f(x,y,z)
代表函数fff在方向l⃗\vec{l}l的变化率。
性质
dfdl⃗=∂f∂xcosα+∂f∂ycosβ+∂f∂zcosγ=(∂f∂x,∂f∂y,∂f∂z)⋅(cosα,cosβ,cosγ)=∇f⋅n⃗=∣∇f∣cos⟨∇f,l⃗⟩\begin{aligned} \frac{df}{d\vec{l}} &=\frac{\partial f}{\partial x}\cos\alpha+\frac{\partial f}{\partial y}\cos\beta+\frac{\partial f}{\partial z}\cos\gamma \\ \\ &=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})\cdot(\cos\alpha,\cos\beta,\cos\gamma)=\nabla f \cdot\vec{n}=|\nabla f|\cos\lang\nabla f,\vec{l}\rang \end{aligned}dldf=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ=(∂x∂f,∂y∂f,∂z∂f)⋅(cosα,cosβ,cosγ)=∇f⋅n=∣∇f∣cos⟨∇f,l⟩
当l⃗\vec{l}l取fff的梯度方向时,cos⟨∇f,l⃗⟩=1\cos\lang\nabla f,\vec{l}\rang=1cos⟨∇f,l⟩=1,变化率绝对值最大且为正;当l⃗\vec{l}l取fff的负梯度方向时,cos⟨∇f,l⃗⟩=−1\cos\lang\nabla f,\vec{l}\rang=-1cos⟨∇f,l⟩=−1,变化率绝对值最大且为负。
梯度下降
应用场景:求损失函数的最小值。
梯度下降的具体算法实现过程是:
1、确定模型和损失函数;
2、参数初始化,包括:参数、算法终止条件和步长;
3、参数更新θj+1=θj−α∂J∂θj\theta_{j+1}=\theta_j - \alpha \frac{\partial J}{\partial\theta_j}θj+1=θj−α∂θj∂J
4、判断停止条件,若满足,则停止,若不满足,则继续更新。
相关文章:

方向导数与梯度下降
文章目录方向角与方向余弦方向角方向余弦方向导数定义性质梯度下降梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(…...

Java岗面试题--Java基础(日积月累,每日三题)
目录面试题一:Java中有哪些容器(集合类)?追问:Java中的容器,线程安全和线程不安全的分别有哪些?面试题二: HashMap 的实现原理/底层数据结构? JDK1.7 和 JDK1.8追问一&am…...
java基础—Volatile关键字详解
java基础—Volatile关键字详解 文章目录java基础—Volatile关键字详解并发编程的三大特性:volatile的作用是什么volatile如何保证有可见性volatile保证可见性在JMM层面原理volatile保证可见性在CPU层面原理可见性问题的例子volatile如何保证有序性单例模式使用volat…...

内存检测工具Sanitizers
Sanitizers介绍 Sanitizers 是谷歌开源的内存检测工具,包括AddressSanitizer、MemorySanitizer、ThreadSanitizer、LeakSanitizer。 Sanitizers是LLVM的一部分。 gcc4.8:支持Address和Thread Sanitizer。 gcc4.9:支持Leak Sanitizer和UBSani…...

Triton : OpenAI 开发的用于Gpu开发语言
Triton : OpenAI 开发的用于Gpu开发语言https://openai.com/blog/triton/1、介绍 https://openai.com/blog/triton/ 2、git地址 https://github.com/openai/triton 3、论文 http://www.eecs.harvard.edu/~htk/publication/2019-mapl-tillet-kung-cox.pdf SIMD : Single Inst…...
Python文件操作-代码案例
文章目录文件打开文件open写文件上下文管理器第三方库简单应用案例使用python生成二维码使用python操作excel程序员鼓励师学生管理系统文件 变量就在内存中,文件在硬盘中. 内存空间更小,访问速度快,成本贵,数据容易丢失,硬盘空间大,访问慢,偏移,持久化存储. \\在才是 \的含义…...

活动目录(Active Directory)管理,AD自动化
每个IT管理员几乎每天都在Active Directory管理中面临许多挑战,尤其是在管理Active Directory用户帐户方面。手动配置用户属性非常耗时、令人厌烦且容易出错,尤其是在大型、复杂的 Windows 网络中。Active Directory管理员和IT经理大多必须执行重复和世俗…...
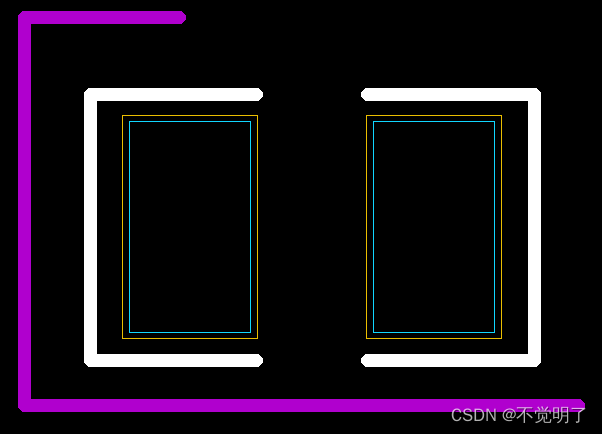
Allegro如何使用Vertext命令修改丝印线段的形状操作指导
Allegro如何使用Vertext命令修改丝印线段的形状操作指导 在用Allegro画丝印线段的时候,如果画了一段不是自己需要形状的线段,无需删除重画,可以用Vertext命令直接编辑 如下图 修改前 修改后 具体操作如下 选择Edit...

Leetcode力扣秋招刷题路-0030
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 30. 串联所有单词的子串 给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。 s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。…...
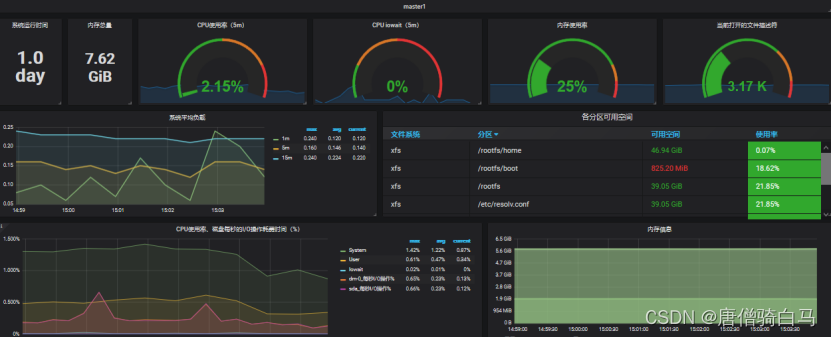
基于Prometheus和k8s搭建监控系统
文章目录1、实验环境2、Prometheus介绍?3、Prometheus特点3.1 样本4、Prometheus组件介绍5、Prometheus和zabbix对比分析6、Prometheus的几种部署模式6.1 基本高可用模式6.2 基本高可用远程存储6.3 基本HA 远程存储 联邦集群方案7、Prometheus的四种数据类型7.1 C…...
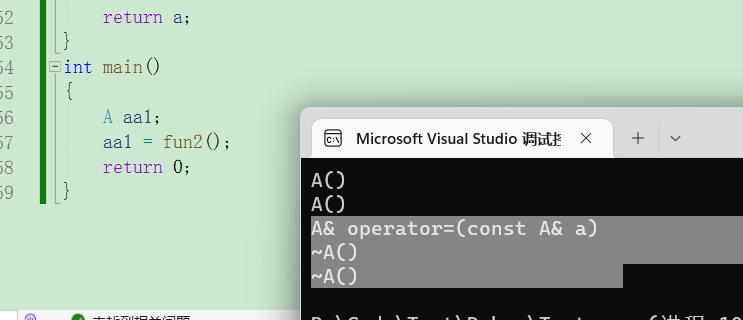
类和对象(下)
类和对象(下)再谈构造函数构造函数体赋值初始化列表explicit关键字static成员静态成员的特性友元友元函数友元类成员函数做友元内部类匿名对象编译器的一些优化再谈构造函数 构造函数体赋值 在创建对象的时候编译器会调用构造函数给对象中的成员变量一…...

达梦数据库单机部署
一、安装前准备 1. 安装环境 操作系统:redhat7.9 达梦数据库版本:V8 内存:2G CPU:x86_64 2. 新建用户组和用户 groupadd dinstall useradd -g dinstall -m -d /home/dmdba -S /bin/bash dmdba passwd dmdba3. 配置参数 vi /etc/security/limits.conf #在末尾添加以下内…...
状态和路由)
从零到一学习Flutter——(二)状态和路由
背景 前文提到了Widget的状态,在Flutter中一切都是Widget,那么由Widget组成的页面,会有很多复杂的父子关系,要想交互友好,则需要这些Widget进行通讯,也就是所谓的状态管理。 同时在了解了布局之后,我们会写出很多的页面,那么在这些页面切换,也是一个很重要的能力。 …...
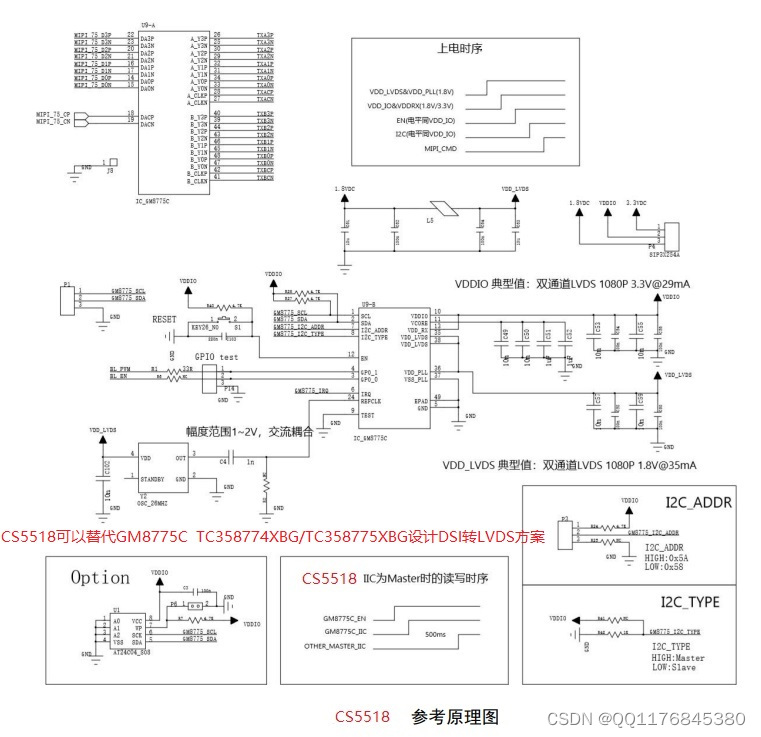
TC358774XBG/TC358775XBG替代方案|CS5518替代TC358774XBG/TC358775XBG设计DSI转LVSD设计资料
TC358774XBG/TC358775XBG替代方案|CS5518替代TC358774XBG/TC358775XBG设计DSI转LVSD设计资料 TC358774XBG/TC358775XBG 芯片的主要功能是作为 DSI - LVDS 通信协议桥接,主芯片的视频数据可通过 DSI 链路流 出,以驱动兼容 LVDS 的显示板。换句话说&#x…...
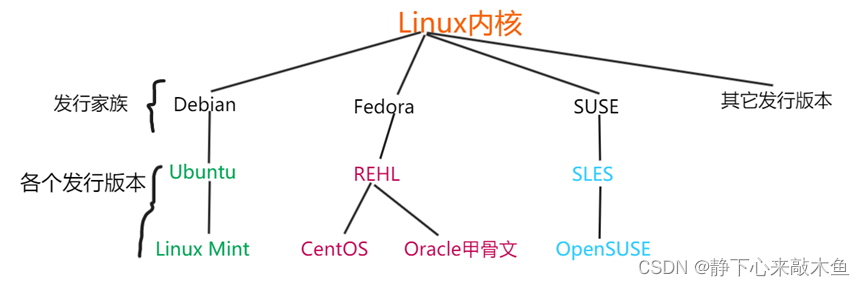
Linux---Kernal与Shell讲解
目录 Shell简介 什么是Shell Shell分类 内核Kernal Shell简介 什么是Shell 我们首先需要知道一台完整的计算机是由硬件组成的,而人不可以直接与硬件交互,为了完成交互,进行了以下的操作 将硬件设备交由内核管理,给硬件套个内…...
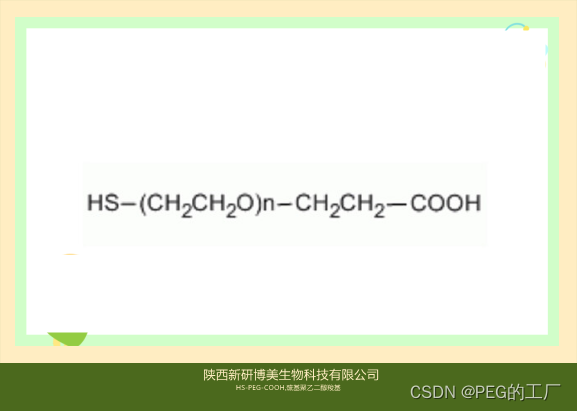
Thiol-PEG-Acid,HS-PEG-COOH,巯基-聚乙二醇-羧基试剂供应
一:产品描述 1、名称 英文:HS-PEG-COOH,Thiol-PEG-Acid 中文:巯基-聚乙二醇-羧基 2、CAS编号:N/A 3、所属分类:Carboxylic acid PEG Thiol PEG 4、分子量:可定制,Thiol-聚乙二…...
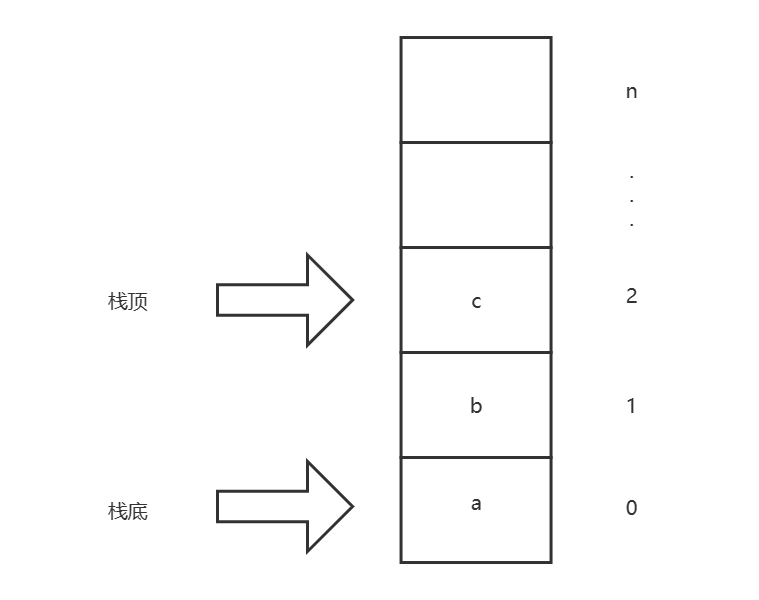
数据结构与算法基础-学习-09-线性表之栈的理解、初始化顺序栈、判断顺序栈空、获取顺序栈长度的实现
一、个人理解栈是线性表的一种衍生,和之前的顺序表和链表在插入和删除元素上有较大差异,其他基本相同,栈是数据只能插入表的尾部(栈顶),删除数据时只能删除表的尾部(栈顶)数据&#…...
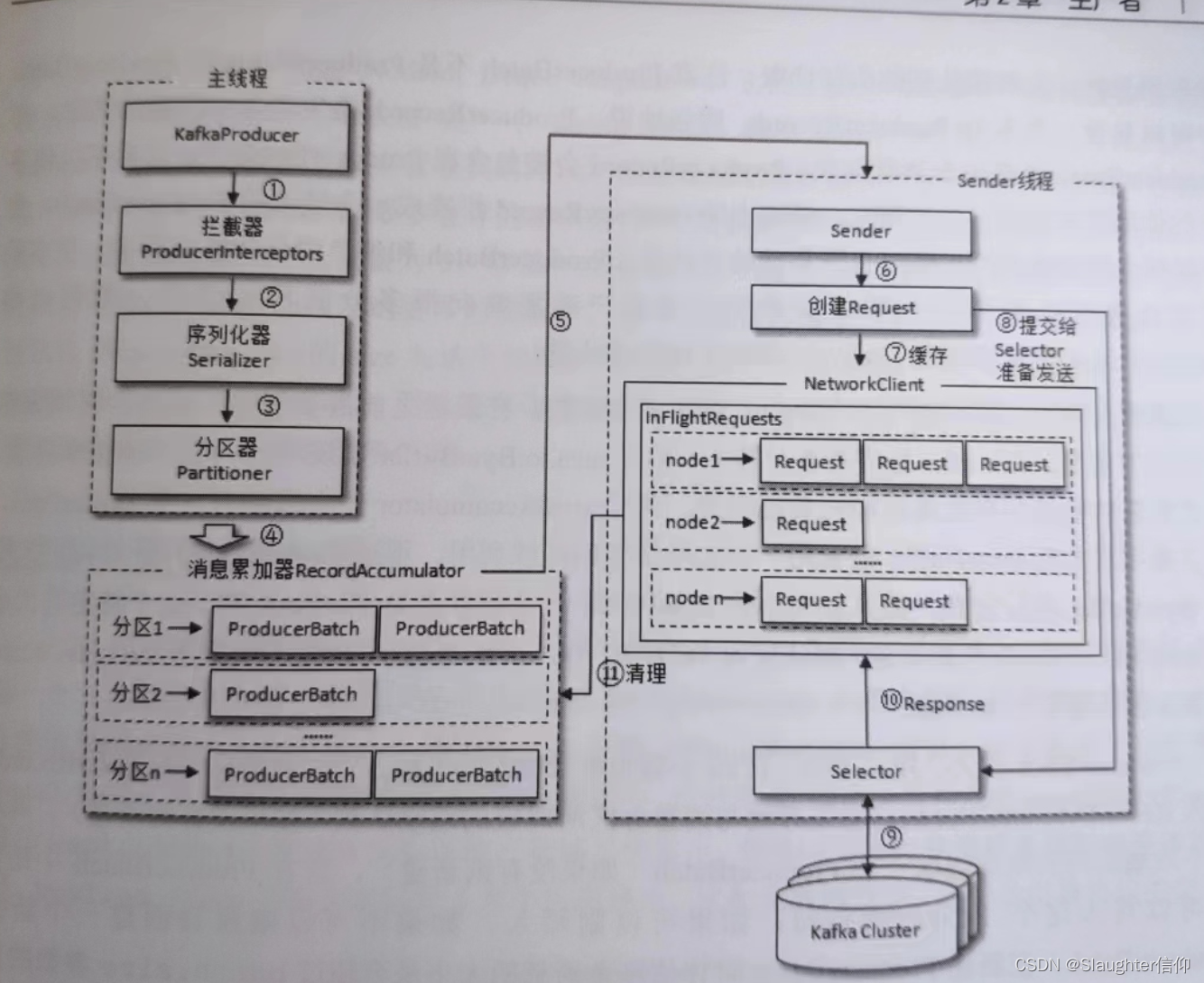
深入Kafka核心设计与实践原理读书笔记第二章
1 生产者 生产逻辑 配置生产者客户端参数及创建相应的生产者实例。构建待发送的消息。发送消息关闭实列 参数说明 bootstrap.servers :用来指定生产者客户端链接Kafka集群搜需要的broker地址清单,具体格式 host1:port1,host2:port2,可以设置一个或多…...

知乎kol投放怎么做?知乎kol资源从哪里找?
每个领域都有一些比较专业且具有话语权的大V博主,他们推荐某个产品或是品牌就能对粉丝产生很深的影响力,影响用户消费决策。 互联网时代,每个热门的内容平台上都活跃着一大批kol博主,做kol投放具有很高的商业价值。 知乎内容社区…...

python设计模式-享元设计模式,抽象工厂设计模式,面向对象设计模式
享元设计模式 享元(flyweight)设计模式属于结构设计模式类别。 它提供了一种减少对象数的方法。 它包含各种有助于改进应用程序结构的功能。享元对象最重要的特性是不可变的。 这意味着一旦构建就不能修改它们。 该模式使用HashMap来存储引用对象 如何实现享元(flyweight)设计…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
