推挽电路---采用二极管消除交越失真----克服交越失真的互补推挽输出电路图
交越失真产生的原因及消除方法
由于晶体管的门限电压不为零,比如一般的硅三极管,NPN型在0.7V以上才导通,这样在00.7就存在死区,不能完全模拟出输入信号波形,PNP型小于-0.7V才导通,比如当输入的交流的正弦波时,在-0.70.7之间两个管子都不能导通,输出波形对输入波形来说这就存在失真,即为交越失真。
消除交越失真的视频讲解
克服交越失真的措施是:避开死区电压区,使每一晶体管处于微导通状态,一旦加入输入信号,使其马上进入线性工作区
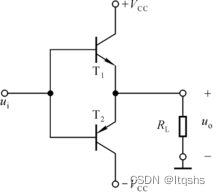
产生交越失真的电路
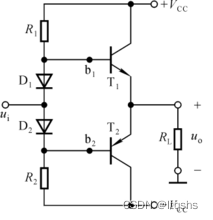
消除交越失真的电路
提供给晶体管静态偏置使其微导通有三种途径:(1)利用二极管和电阻的压降产生偏置电压;(2)利用VBE扩大电路产生偏置电压(3)利用电阻上的压降产生偏置电压。
交越失真出现在乙类放大电路,甲类放大电路失真最小但是效率较低10%左右,乙类有交越失真但是其效率高,所以出现了甲乙类放大电路,比甲类效率高,比乙类失真小。
参考原文:《交越失真及产生原因和改善方法》
克服交越失真的互补推挽输出电路图
摘要: 如图所示为克服交越失真的互补推挽输出电路。为克服交越失真,需在输出管VT2,VT3的基极上各加上一个大于等于三极管导通电压的正向偏压(如硅管为0.6V或0.7V,锗管为0.2V或0.3V)。图中的VT4,R1,R2组成固定恒压偏置电路,可给VT2,VT3的基极加一个固定偏压,从而保证了输人信号ui为正弦信号时,输出信号uo为不失真的正弦信号,即克服了交越失真。图 克服交越失真的互补推挽输出电路来源
如图所示为克服交越失真的互补推挽输出电路。
为克服交越失真,需在输出管VT2,VT3的基极上各加上一个大于等于三极管导通电压的正向偏压(如硅管为0.6V或0.7V,锗管为0.2V或0.3V)。图中的VT4,R1,R2组成固定恒压偏置电路,可给VT2,VT3的基极加一个固定偏压,从而保证了输人信号ui为正弦信号时,输出信号uo为不失真的正弦信号,即克服了交越失真。
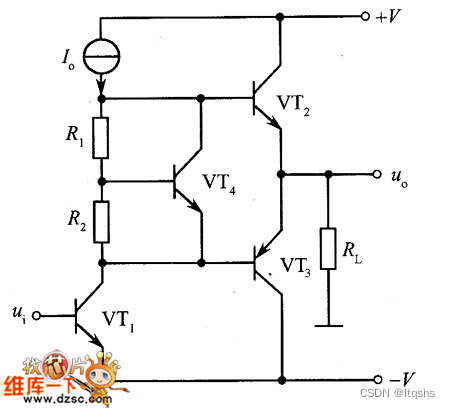
图 克服交越失真的互补推挽输出电路
参考原文:《克服交越失真的互补推挽输出电路图》
相关文章:

推挽电路---采用二极管消除交越失真----克服交越失真的互补推挽输出电路图
交越失真产生的原因及消除方法 由于晶体管的门限电压不为零,比如一般的硅三极管,NPN型在0.7V以上才导通,这样在00.7就存在死区,不能完全模拟出输入信号波形,PNP型小于-0.7V才导通,比如当输入的交流的正弦波…...

day11_面向对象
今日内容 零、 复习昨日 一、一日一题(数组,OOP) 二、面向对象练习(方法参数返回值) 三、局部变量&成员变量 四、this关键字 五、构造方法 六、重载 七、封装 小破站同步上课视频: https://space.bilibili.com/402601570/channel/collectiondetail?…...
大数据处理学习笔记1.1 搭建Scala开发环境
文章目录零、本讲学习目标一、Scala简介(一)Scala概述(二)函数式编程(三)Scala特性1、一切都是对象2、一切都是函数3、一切都是表达式(四)在线运行Scala二、选择Scala版本三、Window…...

VSCODE C++ 调用matplotlibcpp画图
使用VSCODE编写C程序,想在调试过程中看中间数据的波形,于是找到了python的matplotlibcpp库,参考文章链接是:https://blog.csdn.net/weixin_43769166/article/details/118365416;按照他的步骤配置好之后,跳出…...
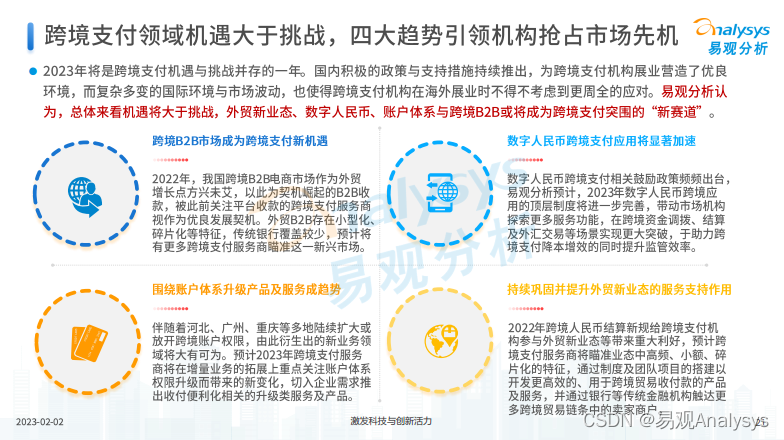
面对“开门红”,跨境支付如何寻求新增长曲线?
易观:2022年是第三方支付行业洗牌加剧的一年,在部分机构选择退出的过程中,也有机构开始瞄准跨境业务,成为了支付机构转型的重要方向之一。跨境支付是指两个或及其以上的国家或地区进行国际贸易、国际投资或其他经济活动࿰…...
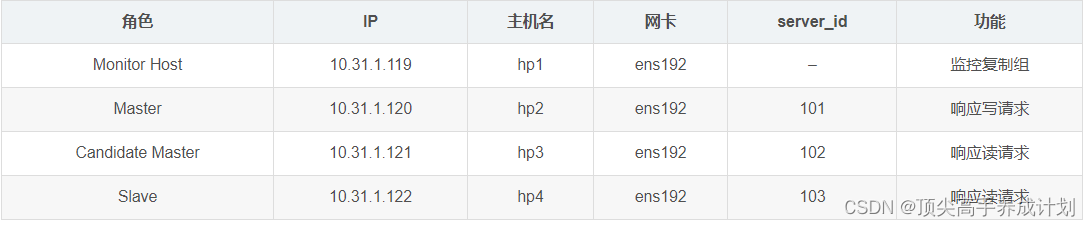
MySQL入门篇-MySQL MHA高可用实战
MHA简介 MHA(Master High Availability)目前在MySQL高可用方面是一个相对成熟的解决方案,它由日本DeNA公司的youshimaton(现就职于Facebook公司)开发,是一套优秀的作为MySQL高可用性环境下故障切换和主从提…...
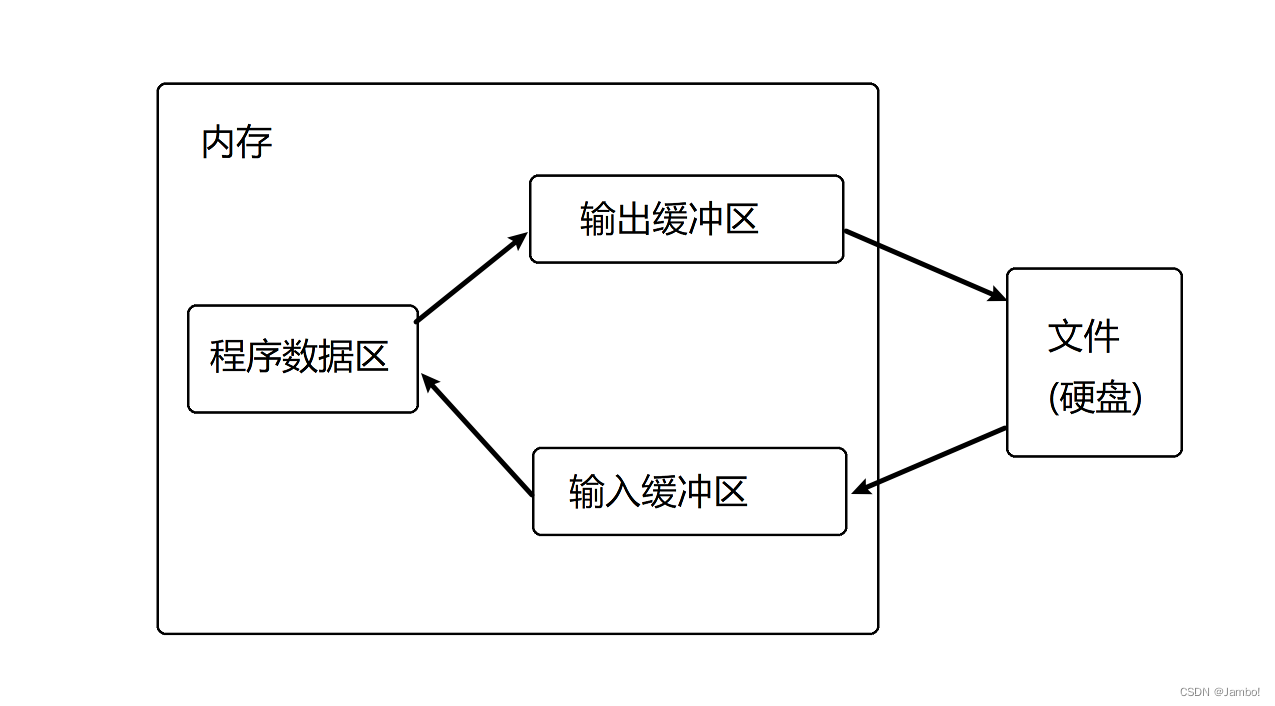
C语言文件操作
目录1.文件指针2.文件的打开和关闭3.文件的读写3.1文件的顺序读写fgetc和fputcfgets和fputsfscanf和fprintffread和fwrite3.2文件的随机读写fseekftellrewind4.文本文件和二进制文件5.文件读取结束的判定6.文件缓冲区1.文件指针 在文件操作中,一个关键的概念是文件…...
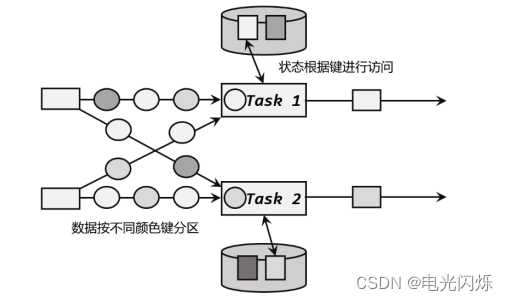
Flink中核心重点总结
目录 1. 算子链 1.1. 一对一(One-to-one, forwarding) 1.2. 重分区(Redistributing) 1.3. 为什么有算子链 2. 物理分区(Physical Partitioning) 2.1. 什么是分区 2.2. 随机分区ÿ…...

gismo中NURBS的相关函数的使用---待完善
文章目录 前言一、B样条的求值1.1 节点向量的生成1.2 基函数的调用1.3 函数里面的T指的是系数类型二、以等几何两个单元12个控制点为例输出的控制点坐标有误1.4二、#pic_center <table><tr><td bgcolor=PowderBlue>二维数2.12.22.32.4三、3.13.23.33.4四、4.…...

5.数据共享与持久化
数据共享与持久化 在容器中管理数据主要有两种方式: 数据卷(Data Volumes)挂载主机目录 (Bind mounts) 数据卷 数据卷是一个可供一个或多个容器使用的特殊目录,它绕过UFS,可以提供很多有用的特性: 数据…...

RabbitMQ-客户端源码之AMQCommand
AMQCommand不是直接包含Method等成员变量的,而是通过CommandAssembler又做了一次封装。 接下来先看下CommandAssembler类。此类中有这些成员变量: /** Current state, used to decide how to handle each incoming frame. */ private enum CAState {EXP…...

linux设置登录失败处理功能(密码错误次数限制、pam_tally2.so模块)和操作超时退出功能(/etc/profile)
一、登录失败处理功能策略 1、登录失败处理功能策略(服务器终端) (1)编辑系统/etc/pam.d/system-auth 文件,在 auth 字段所在的那一部分添加如下pam_tally2.so模块的策略参数: auth required pam_tally2…...

Centos7上Docker安装
文章目录1.Docker常识2.安装Docker1.卸载旧版本Docker2.安装Docker3.启动Docker4.配置镜像加速前天开学啦~所以可以回来继续卷了哈哈哈,放假在家效率不高,在学校事情也少点(^_−)☆昨天和今天学了学Docker相关的知识,也算是简单了解了下&…...

新瑞鹏“狂飙”,宠物医疗是门好生意吗?
宠物看病比人还贵,正在让不少年轻一族陷入尴尬境地。在知乎上,有个高赞提问叫“你愿意花光积蓄,给宠物治病吗”,这个在老一辈人看来不可思议的魔幻选择,真实地发生在当下的年轻人身上。提问底下,有人表示自…...
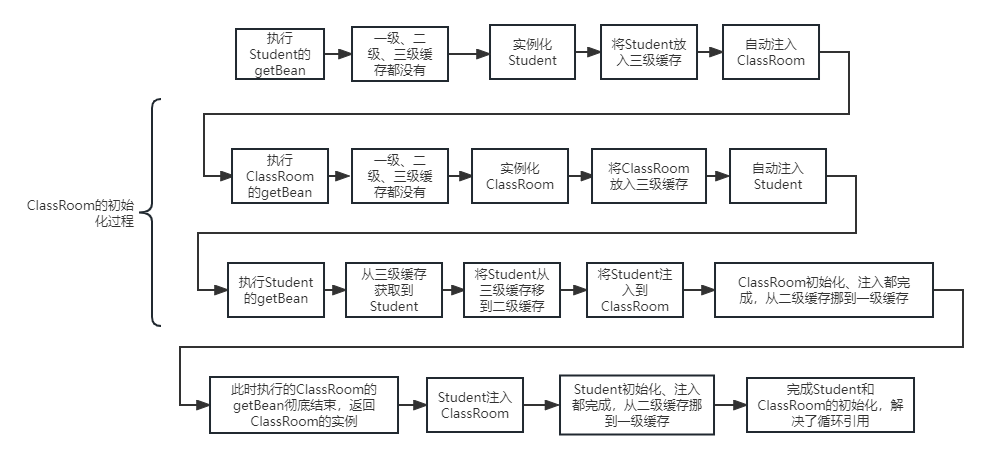
Spring循环依赖问题,Spring是如何解决循环依赖的?
文章目录一、什么是循环依赖1、代码实例2、重要信息二、源码分析1、初始化Student对Student中的ClassRoom进行Autowire操作2、Student的自动注入ClassRoom时,又对ClassRoom的初始化3、ClassRoom的初始化,又执行自动注入Student的逻辑4、Student注入Class…...
更改SAP GUI登录界面信息
在SAP GUI的登录界面,左部输入登录信息如客户端、用户名、密码等,右部空余部分可维护一些登录信息文本,如登录的产品、客户端说明及注意事项等,此项操作详见SAP Notes 205487 – Own text on SAPGui logon screen 维护文档使用的…...
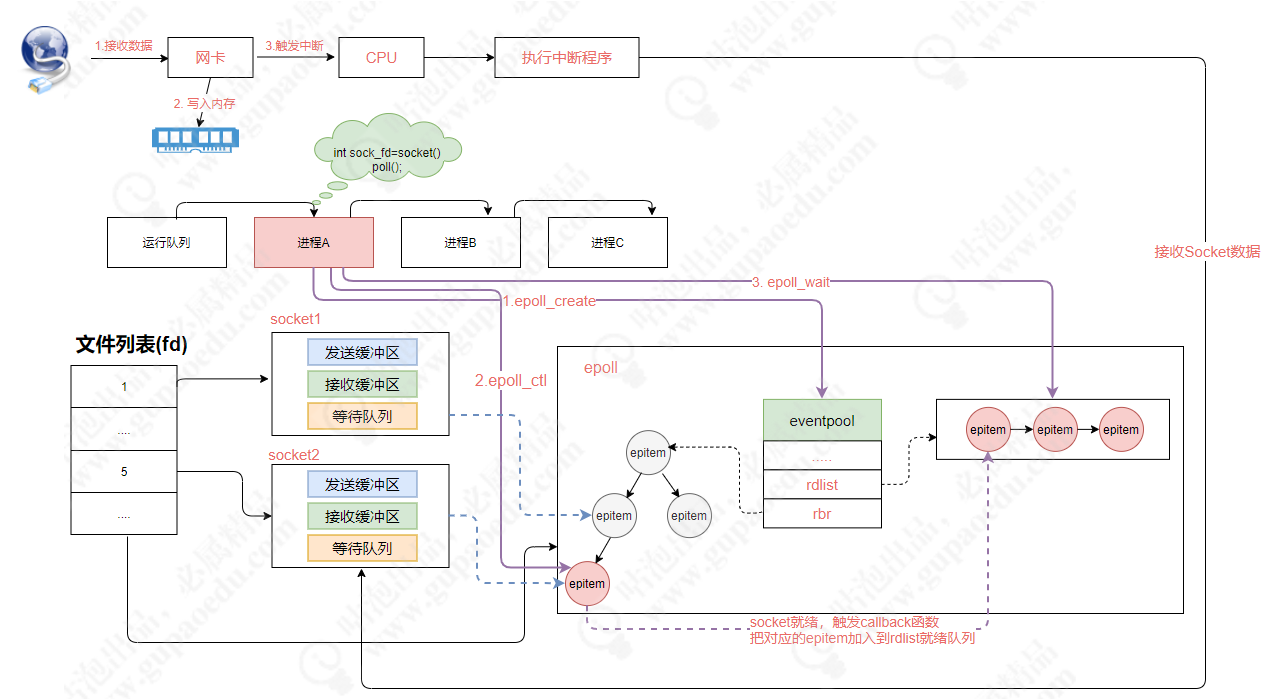
分布式微服务架构下网络通信的底层实现原理
在分布式架构中,网络通信是底层基础,没有网络,也就没有所谓的分布式架构。只有通过网络才能使得一大片机器互相协作,共同完成一件事情。 同样,在大规模的系统架构中,应用吞吐量上不去、网络存在通信延迟、我…...

进大厂必备的Java面试八股文大全(2023最新精简易懂版,八股文中的八股文)
为什么同样是跳槽,有些人薪资能翻三倍?” 最近一个粉丝发出了灵魂拷问,类似的问题我收到过很多次,身边也确实有认识的同事、朋友们有非常成功的跳槽经历和收益,先说一个典型例子: 学弟小 A 工作一年半&am…...

都说测试行业饱和了,为什么我们公司给初级测试开到了12K?
故事起因: 最近我有个刚毕业的学生问我说:我感觉现在测试行业已经饱和了,也不是说饱和了,是初级的测试根本就没有公司要,哪怕你不要工资也没公司要你,测试刚学出来,没有任何的项目经验和工作经验…...

解决Idea启动项目失败,提示Error running ‘XXXApplication‘: Command line is too long
IDEA版本为:IntelliJ IDEA 2018.2 (Ultimate Edition)一、问题描述有时当我们使用IDEA,Run/Debug一个SpringBoot项目时,可能会启动失败,并提示以下错误。Error running XXXApplication: Command line is too long. Shorten comman…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
