机器学习强基计划8-1:图解主成分分析PCA算法(附Python实现)
目录
- 0 写在前面
- 1 为什么要降维?
- 2 主成分分析原理
- 3 PCA与SVD的联系
- 4 Python实现
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖,由本人亲自从底层编写、测试与文章配套的各个经典算法,不依赖于现有库,可以大大加深对算法的理解。
🚀详情:机器学习强基计划(附几十种经典模型源码)
1 为什么要降维?
首先考虑单个特征的情形,假设在样本xxx任意小邻域δ\deltaδ内都存在样本,则称对样本空间进行了密采样(dense sample)。例如取δ=0.01\delta =0.01δ=0.01,则在归一化样本平均分布的情况下需要采样100个样本。
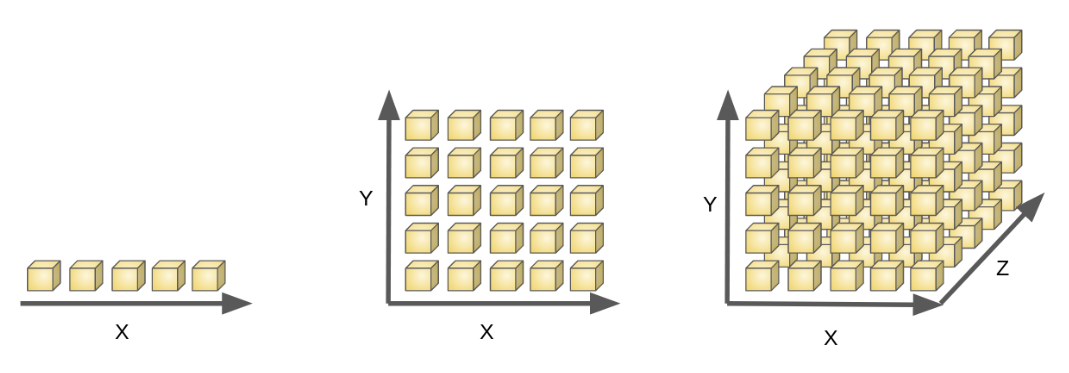
然而,机器学习任务中通常面临高维特征空间,若特征维数为40,则要实现密采样就需要108010^{80}1080个样本——相当于宇宙中基本粒子的总数。所以密采样在高维特征空间中无法实现,换言之,高维特征样本分布非常稀疏,给机器学习训练、算法采样优化带来了困难。
这种高维情形下机器学习任务产生严重障碍现象称为维数灾难(curse of dimensionality),维数灾难还会以指数级的规模造成计算复杂度上升、存储占用大等问题。缓解维数灾难的一个重要途径是降维(dimension reduction),因为样本数据往往以某种与学习任务密切相关的低维分布的形式,嵌入在高维空间内,如图所示。
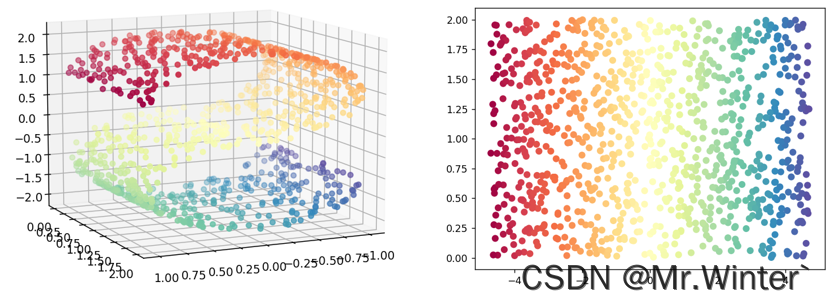
所以降维的核心原理是通过某种数学变换将原始高维特征空间转变为一个更能体现数据本质特征的低维子空间,在这个子空间中样本密度大幅提高,计算复杂度大幅降低,机器学习任务更容易进行。常见的降维技术如表所示
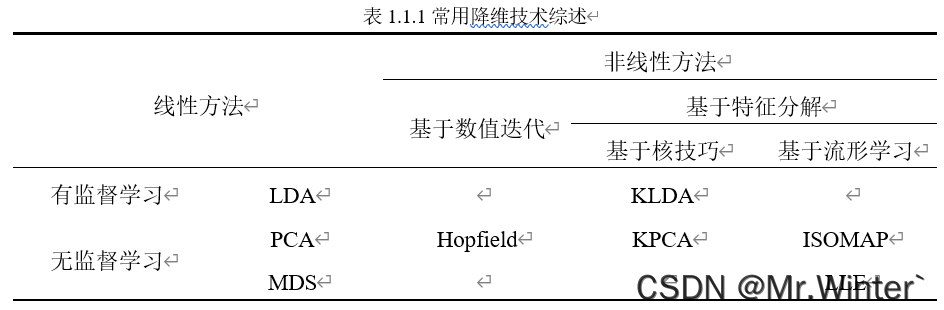
2 主成分分析原理
主成分分析(Principal Component Analysis, PCA)限制样本在经过降维映射W\boldsymbol{W}W得到的低维空间中具有最大可分性和特征最小相关性。
- 最大可分性:指高维样本在低维超平面上的投影应尽可能远离,因为越本质的特征越能将样本区分开
- 特征最小相关性:指量化样本属性的各个特征维度间应尽可能无关,因为特征间无关性越强构成的特征空间信息量越丰富。
满足这两个特性的特征在PCA算法中称为主成分。下面开始算法分析
假设样本X\boldsymbol{X}X经过中心化预处理,则其在低维超平面投影为WTX\boldsymbol{W}^T\boldsymbol{X}WTX,投影协方差矩阵Σ=WTXXTW\boldsymbol{\varSigma }=\boldsymbol{W}^T\boldsymbol{XX}^T\boldsymbol{W}Σ=WTXXTW,其中W=[w1w2⋯wd′]\boldsymbol{W}=\left[ \begin{matrix} \boldsymbol{w}_1& \boldsymbol{w}_2& \cdots& \boldsymbol{w}_{d'}\\\end{matrix} \right]W=[w1w2⋯wd′]为低维空间的单位正交基。
-
考虑到最大可分性则应最大化Σ\boldsymbol{\varSigma }Σ
我们从协方差的物理意义上思考一下为什么协方差小同类样本就接近。如图所示,是同一个三维样本在两个二维平面的投影,可以看出协方差大的样本越细长分散,协方差小则反之。所以协方差小可以使样本更聚合,也即样本投影点尽可能接近。更多协方差相关的内容请参考:机器学习强基计划1-4:从协方差的角度详解线性判别分析原理+Python实现
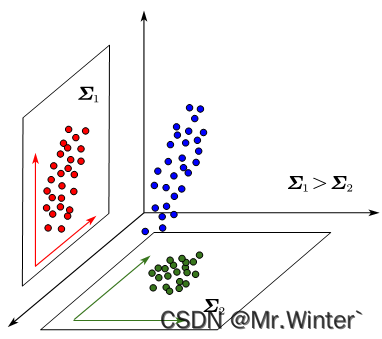
- 考虑到特征最小相关性则应最小化Σ\boldsymbol{\varSigma }Σ的非对角线元素
综上所述,PCA的优化目标为
maxWtr(WTXXTW)s.t.WTW=I\max _{\boldsymbol{W}}\mathrm{tr}\left( \boldsymbol{W}^T\boldsymbol{XX}^T\boldsymbol{W} \right) \,\,\mathrm{s}.\mathrm{t}. \boldsymbol{W}^T\boldsymbol{W}=\boldsymbol{I}Wmaxtr(WTXXTW)s.t.WTW=I
设拉格朗日函数为
L(W,Θ)=tr(WTXXTW)+<Θ,WTW−I>=tr(WTXXTW)+tr(ΘT(WTW−I))\begin{aligned} L\left( \boldsymbol{W},\boldsymbol{\varTheta } \right) &=\mathrm{tr}\left( \boldsymbol{W}^T\boldsymbol{XX}^T\boldsymbol{W} \right) +\left< \boldsymbol{\varTheta },\boldsymbol{W}^T\boldsymbol{W}-\boldsymbol{I} \right> \\&=\mathrm{tr}\left( \boldsymbol{W}^T\boldsymbol{XX}^T\boldsymbol{W} \right) +\mathrm{tr}\left( \boldsymbol{\varTheta }^T\left( \boldsymbol{W}^T\boldsymbol{W}-\boldsymbol{I} \right) \right)\end{aligned}L(W,Θ)=tr(WTXXTW)+⟨Θ,WTW−I⟩=tr(WTXXTW)+tr(ΘT(WTW−I))
对降维映射W\boldsymbol{W}W的约束分为两个:wiTwi=1,wiTwj=0(i=1,2,⋯,d′,i≠j)\boldsymbol{w}_{i}^{T}\boldsymbol{w}_i=1, \boldsymbol{w}_{i}^{T}\boldsymbol{w}_j=0\left( i=1,2,\cdots ,d',i\ne j \right)wiTwi=1,wiTwj=0(i=1,2,⋯,d′,i=j)
先考虑第一个单位化约束,则拉格朗日乘子矩阵退化为对角矩阵Λ\boldsymbol{\varLambda }Λ。现令
∂L(W,Λ)/∂W=2XXTW+2WΛ=0{{\partial L\left( \boldsymbol{W},\boldsymbol{\varLambda } \right)}/{\partial \boldsymbol{W}}}=2\boldsymbol{XX}^T\boldsymbol{W}+2\boldsymbol{W\varLambda }=0∂L(W,Λ)/∂W=2XXTW+2WΛ=0
即得XXTW=−WΛ\boldsymbol{XX}^T\boldsymbol{W}=-\boldsymbol{W\varLambda }XXTW=−WΛ,考察每个wi\boldsymbol{w}_iwi有
XXTwi=−λiwi=λ~iwi\boldsymbol{XX}^T\boldsymbol{w}_i=-\lambda _i\boldsymbol{w}_i=\tilde{\lambda}_i\boldsymbol{w}_iXXTwi=−λiwi=λ~iwi
所以W\boldsymbol{W}W是矩阵XXT∈Rd×d\boldsymbol{XX}^T\in \mathbb{R} ^{d\times d}XXT∈Rd×d进行特征值分解后对应的特征向量组成的矩阵,由于特征值分解可以通过施密特正交化等方式变换为正交矩阵,因此降维映射的wiTwj=0\boldsymbol{w}_{i}^{T}\boldsymbol{w}_j=0wiTwj=0约束也成立。考虑到
tr(WTXXTW)=∑i=1d′wiTXXTwi=∑i=1d′λ~iwiTwi=∑i=1d′λ~i\mathrm{tr}\left( \boldsymbol{W}^T\boldsymbol{XX}^T\boldsymbol{W} \right) =\sum\nolimits_{i=1}^{d'}{\boldsymbol{w}_{i}^{T}\boldsymbol{XX}^T\boldsymbol{w}_i}=\sum\nolimits_{i=1}^{d'}{\tilde{\lambda}_i\boldsymbol{w}_{i}^{T}\boldsymbol{w}_i}=\sum\nolimits_{i=1}^{d'}{\tilde{\lambda}_i}tr(WTXXTW)=∑i=1d′wiTXXTwi=∑i=1d′λ~iwiTwi=∑i=1d′λ~i
因此取d′≪dd'\ll dd′≪d个最大特征值对应的特征向量即可实现目标。
3 PCA与SVD的联系
PCA与SVD有一定联系:PCA降维需要求解协方差矩阵XXT\boldsymbol{XX}^TXXT,而SVD分解的过程中需要求解AAT\boldsymbol{AA}^TAAT与ATA\boldsymbol{A}^T\boldsymbol{A}ATA,因此如果令A=X\boldsymbol{A}=\boldsymbol{X}A=X,那么SVD的过程中就能得到PCA所需的降维映射W\boldsymbol{W}W。
在大样本下XXT\boldsymbol{XX}^TXXT或AAT\boldsymbol{AA}^TAAT都将产生很高的复杂度,但SVD已有绕过计算XXT\boldsymbol{XX}^TXXT或AAT\boldsymbol{AA}^TAAT直接进行分解的高效算法,因此SVD通常作为求解PCA降维问题的工具,PCA体现了SVD分解中的一个方向(左奇异或右奇异)。
4 Python实现
PCA算法的复现非常简单,核心代码如下
'''
* @breif: 运行降维算法
* @param[in]: outDim -> 输出样本维数
* @retval: Z -> 低维样本集
'''
def run(self, outDim):# 计算协方差矩阵cov = np.dot(self.X, self.X.T)# 特征值分解eigVal, eigVec = np.linalg.eig(cov)# 获取最大的d'个特征值对应的索引, np.argsort是按从小到大排序, 所以对特征值取负号index = np.argsort(-eigVal)[0:outDim]eigVec_ = eigVec[:, index]# 计算低维样本Z = np.dot(eigVec_.T, self.X)return Z
以鸢尾花数据集为例执行降维,效果如下
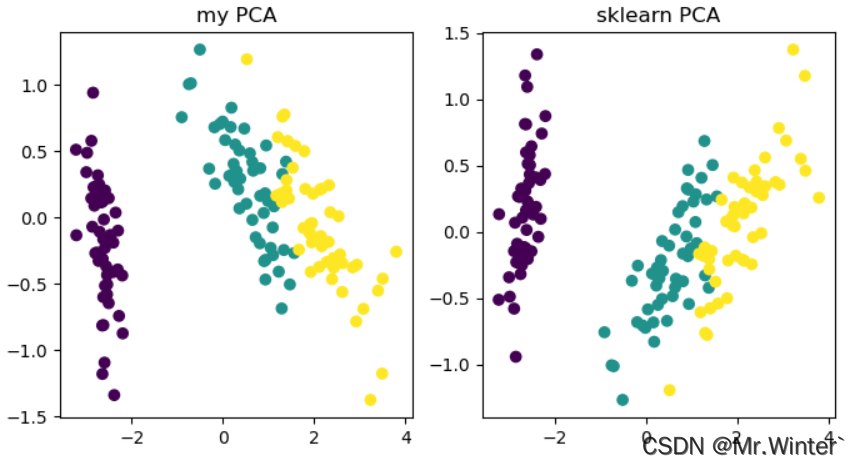
本文完整工程代码请通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

机器学习强基计划8-1:图解主成分分析PCA算法(附Python实现)
目录0 写在前面1 为什么要降维?2 主成分分析原理3 PCA与SVD的联系4 Python实现0 写在前面 机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型…...
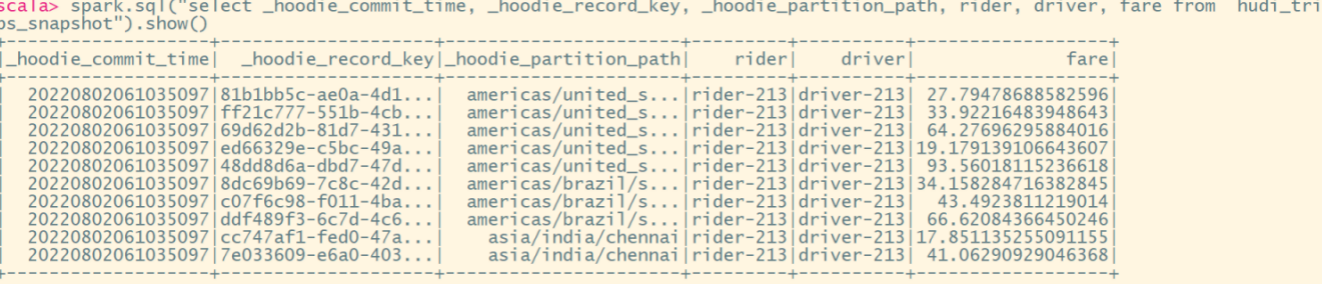
Hudi-集成Spark之spark-shell 方式
Hudi集成Spark之spark-shell 方式 启动 spark-shell (1)启动命令 #针对Spark 3.2 spark-shell \--conf spark.serializerorg.apache.spark.serializer.KryoSerializer \--conf spark.sql.catalog.spark_catalogorg.apache.spark.sql.hudi.catalog.Hoo…...

Python爬虫:从js逆向了解西瓜视频的下载链接的生成
前言 最近花费了几天时间,想获取西瓜视频这个平台上某个视频的下载链接,运用js逆向进行获取。其实,如果小编一开始就注意到这一点(就是在做js逆向时,打了断点之后,然后执行相关代码,查看相关变量的值,结果一下子就蹦出很多视频相关的数据,查看了网站下的相关api链接,也…...

Numpy-如何对数组进行切割
前言 本文是该专栏的第24篇,后面会持续分享python的数据分析知识,记得关注。 继上篇文章,详细介绍了使用numpy对数组进行叠加。本文再详细来介绍,使用numpy如何对数组进行切割。说句题外话,前面有重点介绍numpy的各个知识点。 感兴趣的同学,可查看笔者之前写的详细内容…...
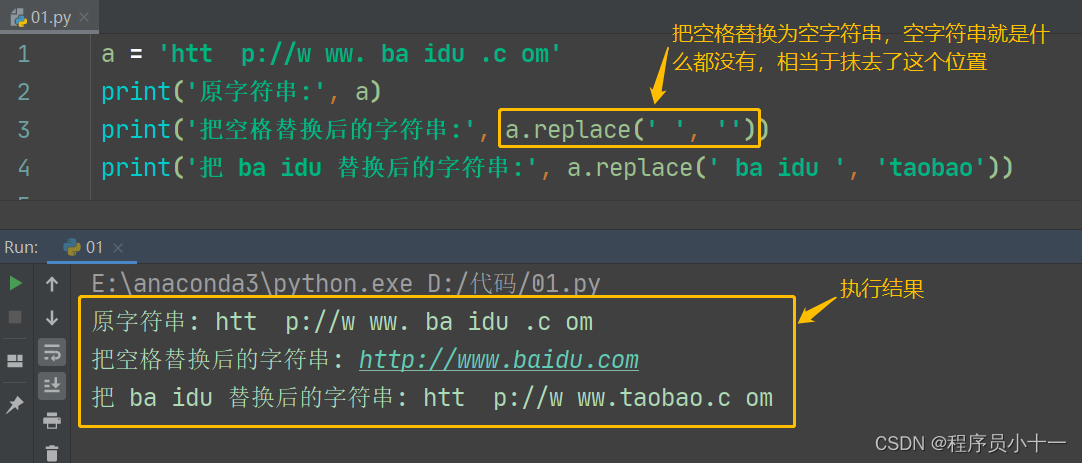
Python之字符串精讲(下)
前言 今天继续讲解字符串下半部分,内容包括字符串的检索、大小写转换、去除字符串中空格和特殊字符。 一、检索字符串 在Python中,字符串对象提供了很多用于字符串查找的方法,主要给大家介绍以下几种方法。 1. count() 方法 count() 方法…...

Python图像卡通化animegan2-pytorch实例演示
先看下效果图: 左边是原图,右边是处理后的图片,使用的 face_paint_512_v2 模型。 项目获取: animegan2-pytorch 下载解压后 cmd 可进入项目地址的命令界面。 其中 img 是我自己建的,用于存放图片。 需要 torch 版本 …...
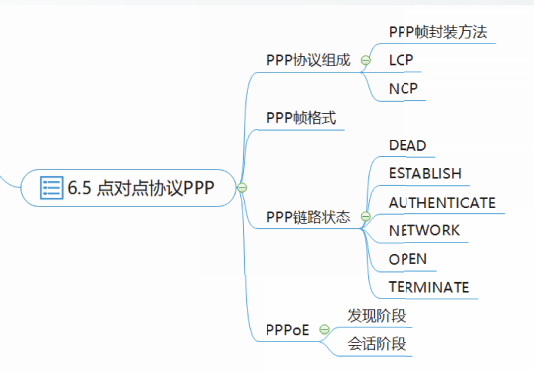
谢希仁版《计算机网络》期末总复习【完结】
文章目录说明第一章 计算机网络概述计算机网络和互联网网络边缘网络核心分组交换网的性能网络体系结构控制平面和数据平面第二章 IP地址分类编址子网划分无分类编址特殊用途的IP地址IP地址规划和分配第三章 应用层应用层协议原理万维网【URL / HTML / HTTP】域名系统DNS动态主机…...

问:React的useState和setState到底是同步还是异步呢?
先来思考一个老生常谈的问题,setState是同步还是异步? 再深入思考一下,useState是同步还是异步呢? 我们来写几个 demo 试验一下。 先看 useState 同步和异步情况下,连续执行两个 useState 示例 function Component() {const…...
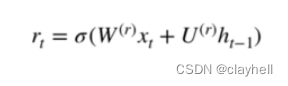
深度理解机器学习16-门控循环单元
评估简单循环神经网络的缺点。 描述门控循环单元(Gated Recurrent Unit,GRU)的架构。 使用GRU进行情绪分析。 将GRU应用于文本生成。 基本RNN通常由输入层、输出层和几个互连的隐藏层组成。最简单的RNN有一个缺点,那就是它们不…...

Python中Generators教程
要想创建一个iterator,必须实现一个有__iter__()和__next__()方法的类,类要能够跟踪内部状态并且在没有元素返回的时候引发StopIteration异常. 这个过程很繁琐而且违反直觉.Generator能够解决这个问题. python generator是一个简单的创建iterator的途径…...

数据结构与算法基础-学习-10-线性表之栈的清理、销毁、压栈、弹栈
一、函数实现1、ClearSqStack(1)用途清理栈的空间。只需要栈顶指针和栈底指针相等,就说明栈已经清空,后续新入栈的数据可以直接覆盖,不用实际清理数据,提升了清理效率。(2)源码Statu…...

Leetcode 每日一题 1234. 替换子串得到平衡字符串
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

【MYSQL中级篇】数据库数据查询学习
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 相关文章 文章名文章地址【MYSQL初级篇】入门…...
)
华为OD机试真题JAVA实现【火星文计算】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述示例一输入输出说明解题思路核心知识点Code运行结果版...

Linux基础知识
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...
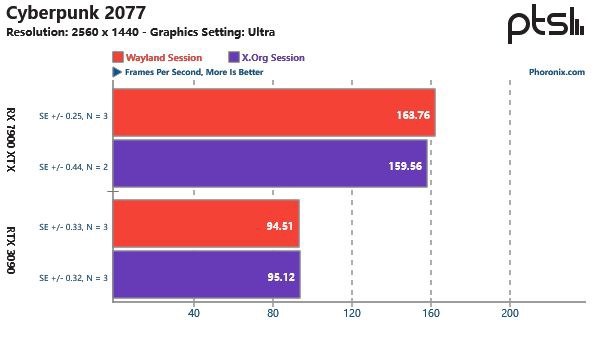
Linux 游戏性能谁的 更优秀X.Org还是Wayland!
导读X.Org 和 Wayland 是目前 Linux 平台上的两大主流显示服务器,那么两者在 Linux 游戏性能上谁更优秀呢?国外科技媒体 Phoronix 在 Ubuntu 22.10 上对其进行了多款游戏的实测。评测在运行 GNOME 43.1 的 Ubuntu 22.10 上进行测试,在安装英伟…...

【数据结构】算法的复杂度分析:让你拥有未卜先知的能力
👑专栏内容:数据结构⛪个人主页:子夜的星的主页💕座右铭:日拱一卒,功不唐捐 文章目录一、前言二、时间复杂度1、定义2、大O的渐进表示法3、常见的时间复杂度三、空间复杂度1、定义2、常见的空间复杂度一、前…...
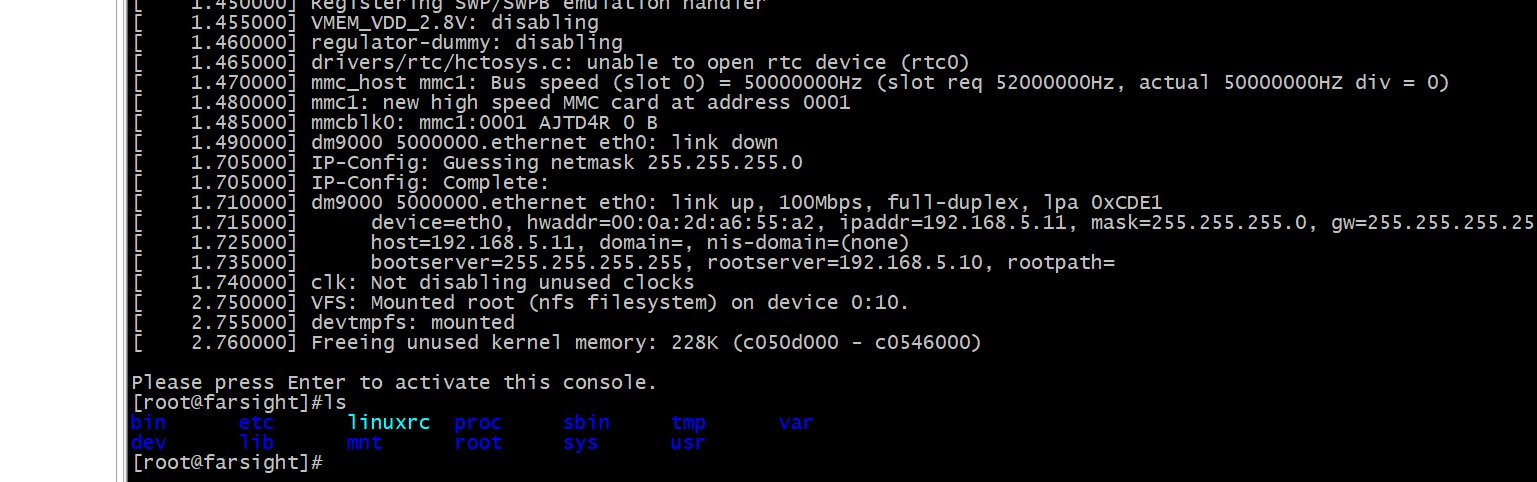
Linux根文件系统移植
目录 一、根文件系统 1.1根文件系统 1.2根文件系统内容 二、根文件系统移植 2.1BusyBox 2.2BusyBox的获取 2.3BusyBox的使用 2.4make menuconfig 2.5编译和安装 2.6修改根文件系统 一、根文件系统 1.1根文件系统 根文件系统是内核启动后挂载的第一个文件系统系统引…...
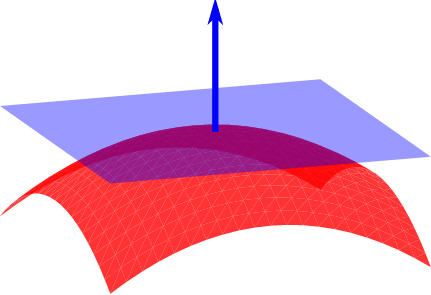
Three.js 无限平面快速教程【Plane】
Three.js 提供了 Plane 概念来表示在 3d 空间中无限延伸的二维表面。 这对于光标交互很有用,因此你可能需要了解如何设置此平面、将其可视化并根据需要进行调整。 推荐:使用 NSDT场景设计器 快速搭建 3D场景。 Three.js 的 Plane 文档很好而且准确&…...
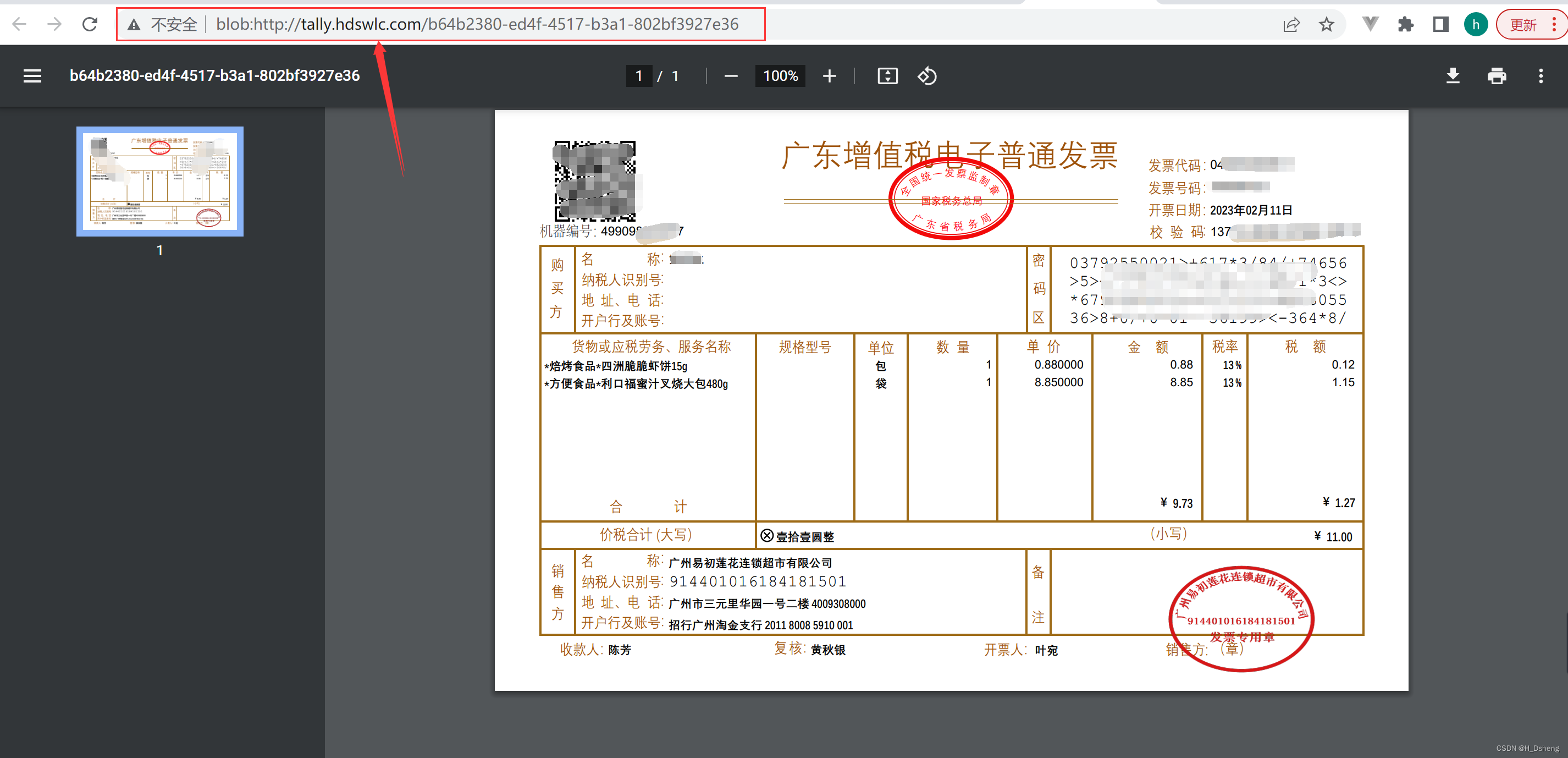
在线预览PDF文件、图片,并且预览地址不显示文件或图片的真实路径。
实现在线预览PDF文件、图片,并且预览地址不显示文件或图片的真实路径。1、vue使用blob流在线预览PDF、图片(包括jpg、png等格式)。1、按钮的方法:2、方法详细:(此方法可以在发起请求时携带token,…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
