R数据分析:孟德尔随机化中介的原理和实操
中介本身就是回归,基本上我看到的很多的调查性研究中在中介分析的方法部分都不会去提混杂,都是默认一个三角形画好,中介关系就算过去了,这里面默认的逻辑就是前两步回归中的混杂是一样的,计算中介效应的时候就自动消掉了。
但是,实际上对不对,还是有待具体分析的:
Traditional, non-instrumental variable methods for mediation analysis experience a number of methodological difficulties, including bias due to confounding between an exposure, mediator and outcome and measurement error
孟德尔随机化作为一个天然的免去混杂的方法,和中介结合,整个中介又变得更纯净了,是一种更加值得推崇的中介做法,也是孟德尔随机化研究的必要的延申。
今天给大家介绍孟德尔随机化中介分析的两个方法multivariable MR (MVMR) and two-step MR
先回顾中介作用
中介分析的基本的概念,就是大家熟悉的三角形:
c是总效应,加上中介变量后,A*B是间接效应,C'是直接效应,有总效应=间接效应+直接效应。
上图中如果总效应,直接效应和间接效应方向都相同的情况下,我们还可以报告中介效应比例,为间接效应比上总效应。
上面的图中的中介效应成立依赖几个假设:
首先就是没有混杂,包括变量之间没有混杂(或者像前面写的直接抵消);暴露不会造成额外混杂;暴露和中介变量没有交互。
再看孟德尔随机化的优势之一就是不受混杂影响,得到纯净的效应,所以将孟德尔随机化延伸一步去探究中介有天然优势。
MR approach retains the benefits of using genetic instruments for causal inference, such as avoiding bias due to confounding, while allowing for estimation of the different effects required for mediation analysis
multivariable MR
按照传统的回归中介的做法思想,我们如果可以跑多变量孟德尔,就可以做出中介分析的结果,具体就是两个暴露的孟德尔,一个是我们关心的暴露,另一个是中介。
MVMR estimates the “direct” causal effects of each exposure included in the estimation on the outcome, conditional on the other exposures included in the model.
跑多变量孟德尔后我们就可以得到中介模型中的直接效应:
就是说这样子跑下来我们就可以得到下图中的c'(直接效应)和B:
再加上我们单独跑一个暴露到结局的孟德尔,我们就有总效应了,利用总效应减去直接效应我们就可以得到间接效应(有了b,a也就出来了),整个中介分析就跑完了,这个就是多变量孟德尔跑中介分析的逻辑。
MR estimates the “total” effect of the exposure on the outcome, whereas MVMR estimates the “direct” effect of each exposure on the outcome
The genetic instrument for both the primary exposure and the second exposure (mediator) are included as instruments in the analysis . The indirect effect can then be estimated by subtracting the direct effect from the total effect (akin to the difference in coefficients method)
Two-step MR
此方法也可以用来计算中介,分为两步,第一步是计算暴露对中介变量的效应得到a,第二步是计算中介到结局的效应得到b,然后两系数相乘得到中介效应。
用总效应(单独跑一个暴露到结局的孟德尔,我们就有总效应了)减去中介效应后得到直接效应,到这儿所有的系数都有了。
The indirect effect of the exposure on the outcome can then be calculated by multiplying the effect of the exposure on the mediator and the effect of the mediator on the outcome. This is equivalent to the product of coefficients method of mediation analysis.
普通的回归肯定是不能这么做的(要得到系数B必须控制暴露),但是我们是跑的孟德尔,就意味着此时的我们跑出来的暴露到中介的效应A是纯净的,相应地B也是纯净的,所以我们才能这么跑。
两步孟德尔在跑的时候要注意,第二步使用的工具变量需要排除第一步就使用过的,因为合格的工具变量本身就不能重复,按理说两步的工具变量本身不应该存在重复,所以如果有重复在第二步的时候得排除掉。
First, genetic IVs associated with the risk factor are used to determine the causal effect of the risk factor on the potential mediator (step one). Secondly, genetic IVs associated with the potential mediator and independent of those used for step one are used to determine the effect of the potential mediator on the outcome of interest (step two)
上面两种方法都是孟德尔中介做法的思想,具体到操作上会有一些问题,比如用MVMR我们得到直接效应,用总效应减去直接效应我们其实只能得到间接效应的点估计,同样的,Two-step MR也存在这个问题,我们只能得到间接效应的点估计,怎么求标准误,和置信区间是在实操中要解决的问题。
下面给大家介绍几种解决方法。
相关文章:

R数据分析:孟德尔随机化中介的原理和实操
中介本身就是回归,基本上我看到的很多的调查性研究中在中介分析的方法部分都不会去提混杂,都是默认一个三角形画好,中介关系就算过去了,这里面默认的逻辑就是前两步回归中的混杂是一样的,计算中介效应的时候就自动消掉…...

【C++】 类和对象 (下)
文章目录📕再谈构造函数1. 构造函数体赋值2. 初始化列表3. explicit 关键字📕static 成员1. 概念2. static 成员变量3. static 成员函数📕 友元1. 友元函数2. 友元类📕内部类📕编译器优化📕再谈构造函数 1…...

asp获取毫秒时间戳的方法 asp获取13位时间戳的方案
一、背景。时间戳就是计算当前与"1970-01-01 08:00:00"的时间差,在asp中通常是使用Datediff函数来计算两个日期差,代码:timestamp Datediff("s", "1970-01-01 08:00:00",now)返回结果:1675951060可…...
-- Python程序接入MySQL数据库)
Python基础篇(十五)-- Python程序接入MySQL数据库
程序运行时,数据都在内存中,程序终止时,需要将数据保存到磁盘上。为了便于程序保存和读取,并能直接通过条件快速查询到指定数据,数据库(Database)应运而生,本篇主要学习使用Python操作数据库,在…...
程序员不得不知道的 API 接口常识
说实话,我非常希望自己能早点看到本篇文章,大学那个时候懵懵懂懂,跟着网上的免费教程做了一个购物商城就屁颠屁颠往简历上写。 至今我仍清晰地记得,那个电商教程是怎么定义接口的: 管它是增加、修改、删除、带参查询…...
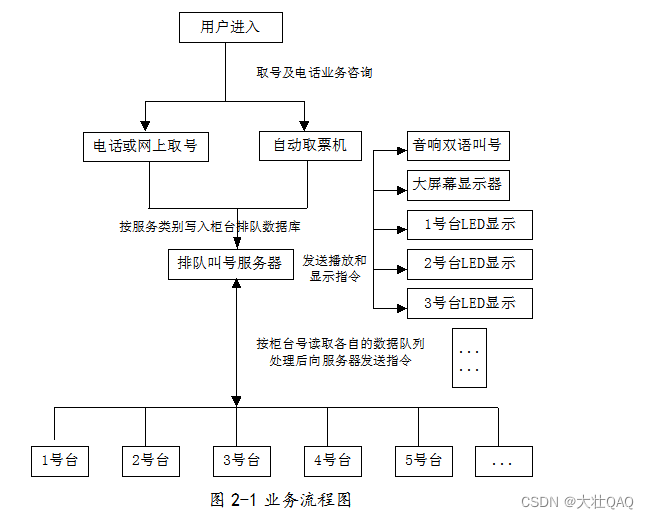
【项目精选】基于Java的银行排号系统的设计与实现
银行排号系统是为解决一些服务业营业大厅排队问题而设计的,它能够有效地提高工作人员的工作效率,也能够使顾客合理的安排等待时间,让顾客感到服务的公平公正。论文首先讨论了排号系统的背景、意义、应用现状以及研究与开发现状。本文在对C/S架…...
前端 基于 vue-simple-uploader 实现大文件断点续传和分片上传
文章目录一、前言二、后端部分新建Maven 项目后端pom.xml配置文件 application.ymlHttpStatus.javaAjaxResult.javaCommonConstant.javaWebConfig.javaCheckChunkVO.javaBackChunk.javaBackFileList.javaBackChunkMapper.javaBackFileListMapper.javaBackFileListMapper.xmlBac…...
解决报错: ERR! code 128npm ERR! An unknown git error occurred
在github下载的项目运行时,进行npm install安装依赖时,出现如下错误:npm ERR! code 128npm ERR! An unknown git error occurrednpm ERR! command git --no-replace-objects ls-remote ssh://gitgithub.com/nhn/raphael.gitnpm ERR! gitgithu…...

聊城高新技术企业认定7项需要注意的问题 山东同邦科技分享
聊城高新技术企业认定7项需要注意的问题 山东同邦科技分享 山东省高新技术企业认定办公室发布《关于开展2021年度本市高新技术企业认定管理工作的通知》,高企认定中有哪些问题需要注意呢?下面我们一起来看一下。 一、知识产权 知识产权数量和质量双达…...

菊乐食品更新IPO招股书:收入依赖单一地区,规模不及认养一头牛
近日,四川菊乐食品股份有限公司(下称“菊乐食品”)预披露更新招股书,准备在深圳证券交易所主板上市,保荐机构为中信建投证券。据贝多财经了解,这已经是菊乐食品第四次冲刺A股上市,此前三次均未能…...

Elasticsearch安装IK分词器、配置自定义分词词库
一、分词简介 在Elasticsearch中,假设搜索条件是“华为手机平板电脑”,要求是只要满足了其中任意一个词语组合的数据都要查询出来。借助 Elasticseach 的文本分析功能可以轻松将搜索条件进行分词处理,再结合倒排索引实现快速检索。Elasticse…...

Linux嵌入式开发——shell脚本
文章目录Linux嵌入式开发——shell脚本一、shell脚本基本原则二、shell脚本语法2.1、编写shell脚本2.2、交互式shell脚本2.3、shell脚本的数值计算2.4、test命令&&运算符||运算符2.5、中括号[]判断符2.6、默认变量三、shell脚本条件判断if thenif then elsecase四、she…...

CV【5】:Layer normalization
系列文章目录 Normalization 系列方法(一):CV【4】:Batch normalization Normalization 系列方法(二):CV【5】:Layer normalization 文章目录系列文章目录前言2. Layer normalizati…...
跳跃游戏 II 解析
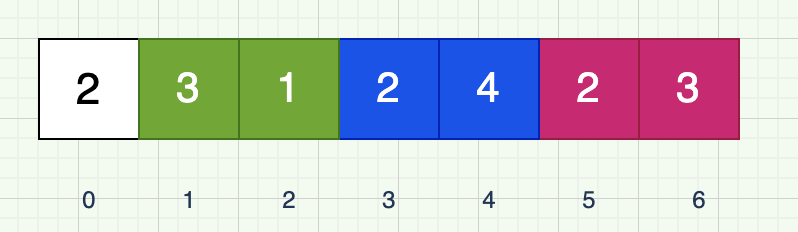
题目描述给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处:0 < j < nums[i] i j < n返回到达 nums[n - 1] 的…...

易基因|猪肠道组织的表观基因组功能注释增强对复杂性状和人类疾病的生物学解释:Nature子刊
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。2021年10月6日,《Nat Commun》杂志发表了题为“Pig genome functional annotation enhances the biological interpretation of complex traits and human disease”的研究论文…...
)
01- NumPy 数据库 (机器学习)
numpy 数据库重点: numpy的主要数据格式: ndarray 列表转化为ndarray格式: np.array() np.save(x_arr, x) # 使用save可以存一个 ndarray np.savetxt(arr.csv, arr, delimiter ,) # 存储为 txt 文件 np.array([1, 2, 5, 8, 19], dtype float32) # 转换…...

RapperBot僵尸网络最新进化:删除恶意软件后仍能访问主机
自 2022 年 6 月中旬以来,研究人员一直在跟踪一个快速发展的 IoT 僵尸网络 RapperBot。该僵尸网络大量借鉴了 Mirai 的源代码,新的样本增加了持久化的功能,保证即使在设备重新启动或者删除恶意软件后,攻击者仍然可以通过 SSH 继续…...
拦截器interceptor总结
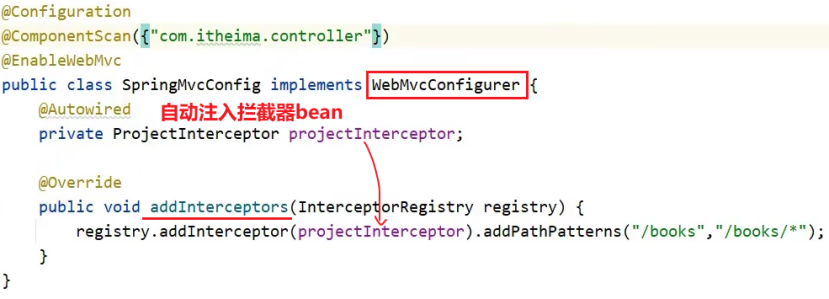
拦截器一. 概念拦截器和AOP的区别:拦截器和过滤器的区别:二. 入门案例2.1 定义拦截器bean2.2 定义配置类2.3 执行流程2.4 简化配置类到SpringMvcConfig中一. 概念 引入: 消息从浏览器发送到后端,请求会先到达Tocmat服务器&#x…...
轻松实现微信小程序上传多文件/图片到腾讯云对象存储COS(免费额度)
概述 对象存储(Cloud Object Storage,COS)是腾讯云提供的一种存储海量文件的分布式存储服务,用户可通过网络随时存储和查看数据。个人账户首次开通COS可以免费领取50GB 标准存储容量包6个月(180天)的额度。…...
)
Golang中defer和return的执行顺序 + 相关测试题(面试常考)
参考文章: 【Golang】defer陷阱和执行原理 GO语言defer和return 的执行顺序 深入理解Golang defer机制,直通面试 面试富途的时候,遇到了1.2的这个进阶问题,没回答出来。这种题简直是 噩梦\color{purple}{噩梦}噩梦,…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
