(1分钟速通面试) 矩阵分解相关内容
矩阵分解算法--总结
QR分解 LU分解
本篇博客总结一下QR分解和LU分解,这些都是矩阵加速的操作,在slam里面还算是比较常用的内容,这个地方在isam的部分出现过。(当然isam也是一个坑,想要出点创新成果的话 可能是不太现实的 短期来讲 哈哈哈)
假定我们能把矩阵A写成下列两个矩阵相乘的形式:A=LU,其中L为下三角矩阵,U为上三角矩阵。这样我们可以把线性方程组Ax= b写成Ax= (LU)x = L(Ux) = b。令Ux = y,则原线性方程组Ax = b可首先求解向量y 使Ly = b,然后求解 Ux = y,从而达到求解线性方程组Ax= b的目的。(非常熟悉的 数值分析课上学的LU分解的形式)

编辑
添加图片注释,不超过 140 字(可选)
LD(LT)的形式,就是把上面的LU分解中拆出来一个倍数矩阵,然后我觉得没啥必要。在这里也放上。
定理:若对称矩阵A的各阶顺序主子式不为零时,则A可以唯一分解为A= LDLT,这里。

编辑
添加图片注释,不超过 140 字(可选)
下面是cholesky分解 读作乔列斯基分解, 栓Q 这些英文名字要是不会读的话 你在讲相关内容的时候就会显得很尴尬 哈哈哈 笑死。
Cholesky分解是一种分解矩阵的方法, 在线形代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积(那实数界来类比的话,此分解就好像求平方根)。与一般的矩阵分解求解方程的方法比较,Cholesky分解效率很高。
对于上面这段定义,让我认知扩充了。上学期学的数值分析里面我知道是转置矩阵,但是没想到是共轭转置矩阵。也就是说一开始我是不知道他还有个共轭的关系在里面的。行了,现在知道了。可能上学期学的内容都是定义在实数域上面的,那么共轭的概念就逐渐被弱化了。现在记住了,原来是共轭转置矩阵。心里默念三遍 hhh
QR分解
矩阵的QR分解是指,可以将矩阵A分级成一个正交阵Q和一个上三角矩阵R的乘积。实际中,QR分解经常被用来解线性最小二乘问题。

编辑
添加图片注释,不超过 140 字(可选)
上面这个就是QR分解,感觉这些的话 会用就行,知道谁的速度快,然后什么情况下的矩阵适合什么样的方法即可。
SVD分解

编辑切换为居中
添加图片注释,不超过 140 字(可选)
说白了,这里的奇异值就是特征值的含义。那么这个矩阵的话,按照我本科的学习思路来说,就是由特征向量和特征值来共同组成的。就是那一套,莱姆大E - A的行列式,求特征值,特征向量,然后就写出来。现在的话,对特征值也是有一定的理解了。特征值可以反应数据的离散情况,也反映了数据的分布 同时可能也反映了数据的趋势。好了,这个特征值的话还是很有用的。在机器学习的一个面试题里面,特征值大的方向,数据会越离散,反之数据会越集中。当然我们研究的话,应该是研究离散的,因为这样好区分。前面这句话主要针对分类来说,因为你的数据离散了,可区分性好了以后,那么我们做分类的效果才显著,这样的研究才有意义。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面这幅图的话 主要说了广义逆矩阵的事情,为啥说是广义呢,因为平时我们定义的逆矩阵一定是一个方阵,这里不是方阵了,那么就称作是广义逆矩阵了。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
本科的时候我们叫他乔丹分解,哈哈哈 就是aj的那个乔丹。笑死。
这个没啥好说的,就是jardon块的构造,这个也是根据特征值的次数来进行构造的。可能再看一看就能想起来相关内容了,所以这里省略。(主要是slam里面好像并不提及这个东西,反正我是没见过 hhh)

编辑
添加图片注释,不超过 140 字(可选)
这里有一个比较。笑死,LU分解最快了。
那在这里对矩阵的分解进行一个总结。也就是说平时我们在解方程组的时候,如果求逆,会加大计算量。我们这时会选择矩阵分解的方法来进行求逆的代替。然后进而求得方程的解。笑死 我想起来上学期的考试,在线LU分解 在线cholesky分解,直接写结果,真的非常方便。如果按照它们的定义一步步地计算的话,我估计最起码20分钟 在不算错的情况下。行了 本篇就讲到这里,这个矩阵分解的内容,opencv也进行了相应地包装。在这里的话不必过多赘述了。栓Q,本篇到此结束。
相关文章:

(1分钟速通面试) 矩阵分解相关内容
矩阵分解算法--总结QR分解 LU分解本篇博客总结一下QR分解和LU分解,这些都是矩阵加速的操作,在slam里面还算是比较常用的内容,这个地方在isam的部分出现过。(当然isam也是一个坑,想要出点创新成果的话 可能是不太现实的 短期来讲 哈…...

this指向
(1)在全局环境中的this——window 无论是否在严格模式下,在全局执行环境中(在任何函数体外部)this 都指向全局对象。 "use strict"console.log(this); //windowconsole.log(thiswindow);//true (…...

安卓小游戏:小板弹球
安卓小游戏:小板弹球 前言 这个是通过自定义View实现小游戏的第三篇,是小时候玩的那种五块钱的游戏机上的,和俄罗斯方块很像,小时候觉得很有意思,就模仿了一下。 需求 这里的逻辑就是板能把球弹起来,球…...
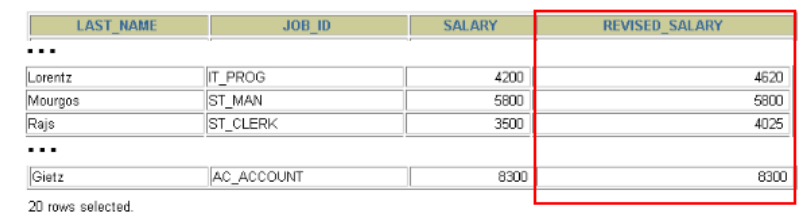
7、单行函数
文章目录1 函数的理解1.1 什么是函数1.2 不同DBMS函数的差异1.3 MySQL的内置函数及分类2 数值函数2.1 基本函数2.2 角度与弧度互换函数2.3 三角函数2.4 指数与对数2.5 进制间的转换3 字符串函数4 日期和时间函数4.1 获取日期、时间4.2 日期与时间戳的转换4.3 获取月份、星期、星…...
)
华为机试题:HJ56 完全数计算(python)
文章目录博主精品专栏导航知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。1.1、input() 与 list(input()) 的区别、及其相互转换方法2、print() :打印输出。3、整型int() :将指定进制…...

opencv——傅里叶变换、低通与高通滤波及直方图等操作
1、傅里叶变换a、傅里叶变换原理时域分析:以时间为参照进行分析。频域分析:相当于上帝视角一样,看事物层次更高,时域的运动在频域来看就是静止的。eg:投球——时域分析:第1分钟投了3分,第2分钟投…...
【NGINX入门指北】 进阶篇
nginx 进阶篇 文章目录nginx 进阶篇一、Nginx Proxy 服务器1、代理原理2、proxy代理3、proxy缓存一、Nginx Proxy 服务器 1、代理原理 正向代理 内网客户机通过代理访问互联网,通常要设置代理服务器地址和端口。 反向代理 外网用户通过代理访问内网服务器&…...

Python中关于@修饰符、yeild关键词、next()函数的基本功能简述
关于修饰符:其实就是将修饰符下面的函数当成参数传给它上面的函数。 def a(x):print(a)adef b():print(b) 其效果等价为: def a(x):print(a)def b():print(b)a(b())有个记忆诀窍,的下面哪个函数最近,谁就是儿子,谁就…...

结合Coverity扫描Spring Boot项目进行Path Manipulation漏洞修复
本篇介绍使用Coverity 扫描基于Spring Boot 项目中的Path Manipulation 漏洞, 进而解决风险,并且可以通过扫描。 什么样的代码会被扫描有路径操纵风险? 在Spring Boot 项目中, 实验了如下的场景: 1. Control 中 file path 作为参数传递的会被扫描,单纯服务方法不会 场…...

【FFMPEG源码分析】从ffplay源码摸清ffmpeg框架(一)
ffplay入口 ffmpeg\fftools\ffplay.c int main(int argc, char **argv) {/*******************start 动态库加载/网络初始化等**************/int flags;VideoState *is;init_dynload();av_log_set_flags(AV_LOG_SKIP_REPEATED);parse_loglevel(argc, argv, options);/* regis…...

C++蓝桥杯 基础练习,高精度加法,输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
C蓝桥杯 基础练习,高精度加法 问题描述 输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。 算法描述 由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。 定义一…...
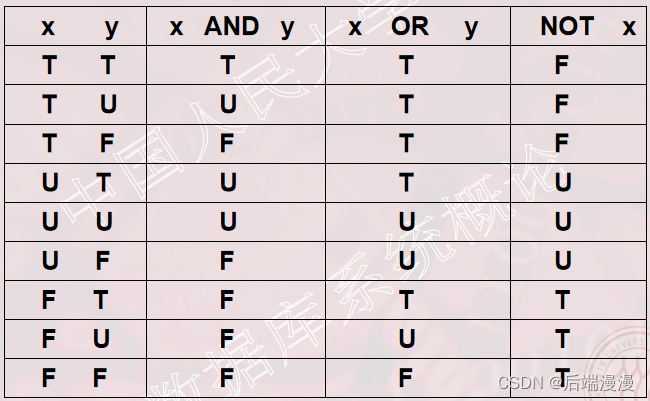
MySQL面试题:SQL语句的基本语法
MySQL目录一、数据库入门1. 数据管理技术的三个阶段2. 关系型数据库与非关系型数据库3. 四大非关系型数据库a. 基于列的数据库(column-oriented)b. 键值对存储(Key-Value Stores)c. 文档存储(Document Storesÿ…...
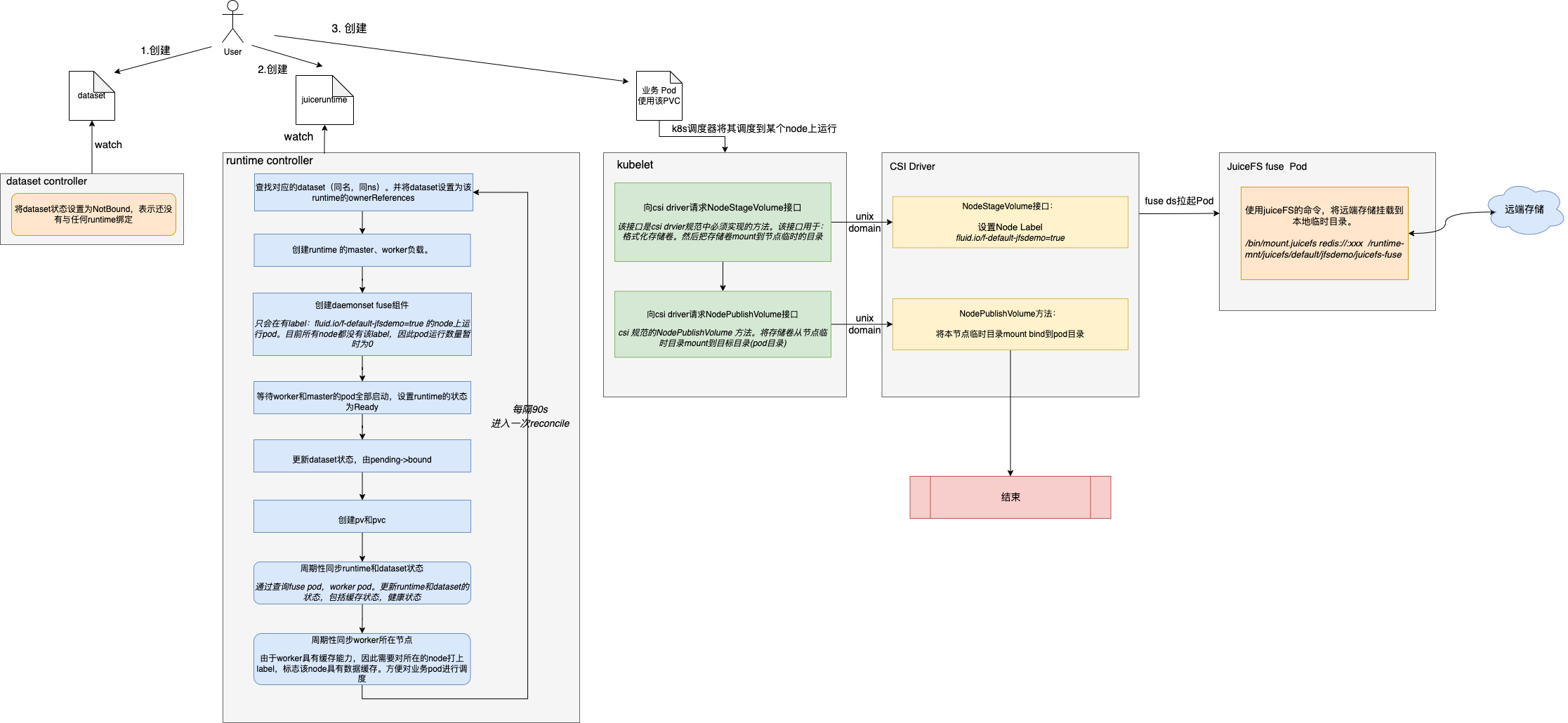
Fluid-数据编排能力原理解析
前言本文对Fluid基础功能-数据编排能力进行原理解析。其中涉及到Fluid架构和k8s csi driver相关知识。建议先了解相关概念,为了便于理解,本文使用JuiceFS作为后端runtime引擎。原理概述Fuild数据编排能力,主要是在云原生环境中,能…...
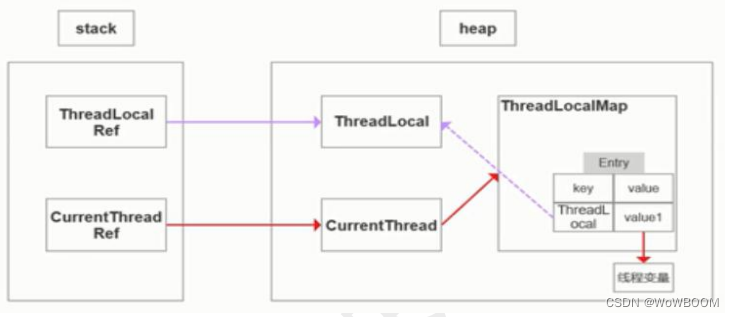
并发线程、锁、ThreadLocal
并发编程并发编程Java内存模型(JMM)并发编程核心问题—可见性、原子性、有序性volatile关键字原子性原子类CAS(Compare-And-Swap 比较并交换)ABA问题Java中的锁乐观锁和悲观锁可重入锁读写锁分段锁自旋锁共享锁/独占锁公平锁/非公平锁偏向锁/轻量级锁/重…...

CMMI-结项管理
结项管理(ProjectClosing Management, PCM)是指在项目开发工作结束后,对项目的有形资产和无形资产进行清算;对项目进行综合评估;总结经验教训等。结项管理过程域是SPP模型的重要组成部分。本规范阐述了结项管理的规程&…...
网络通信协议是什么?
网络通信基本模式 常见的通信模式有如下2种形式:Client-Server(CS) 、 Browser/Server(BS) 实现网络编程关键的三要素 IP地址:设备在网络中的地址,是唯一的标识。 端口:应用程序在设备中唯一的标识。 协议: 数据在网络中传输的…...

阶段5:Java分布式与微服务实战
目录 第33-34周 Spring Cloud电商实战 一、Eureka-server模块开发 1、引入依赖 2、配置文件 3、启动注解 一、Eureka-server模块开发 第33-34周 Spring Cloud电商实战 一、Eureka-server模块开发 1、引入依赖 父项目依赖:cloud-mall-practice springboot的…...

我的创作纪念日
目录 机缘 收获 日常 憧憬 机缘 其实本来从大一上学期后半段(2017)就开始谢谢零星的博客,只不过当时是自己用hexo搭建了一个小网站,还整了个域名:jiayoudangdang.top,虽然这个早就过期; 后来发现了CSDNÿ…...
Qml学习——动态加载控件
最近在学习Qml,但对Qml的各种用法都不太熟悉,总是会搞忘,所以写几篇文章对学习过程中的遇到的东西做一个记录。 学习参考视频:https://www.bilibili.com/video/BV1Ay4y1W7xd?p1&vd_source0b527ff208c63f0b1150450fd7023fd8 目…...

设计模式之职责链模式
什么是职责链模式 职责链模式是避免请求发送者与接受者耦合在一起,让多个对象都可以接受到请求,从而将这些对象连接成一条链,并且沿着这条链传递请求,直到有对象处理为止。 职责链模式包含以下几个角色: …...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
