【别再困扰于LeetCode接雨水问题了 | 从暴力法=>动态规划=>单调栈】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |

🍔 目录
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ 暴力法
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- ⚡ 动态规划
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- ⚡ 单调栈
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- 🍋 总结
- 💬 共勉
🚩 题目链接
- 42. 接雨水
⛲ 题目描述
给定 n 个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
🌟 求解思路&实现代码&运行结果
⚡ 暴力法
🥦 求解思路
暴力法的思路很简单,对于每一个柱子,我们找到其左右两侧的最大高度,分别记为 l e f t M a x leftMax leftMax 和 r i g h t M a x rightMax rightMax,然后计算其储水量 m i n ( l e f t M a x , r i g h t M a x ) − h e i g h t i min(leftMax, rightMax) - height_i min(leftMax,rightMax)−heighti,将所有储水量累加起来即可。
🥦 实现代码
class Solution {public int trap(int[] height) {int n = height.length;int ans = 0;for (int i = 0; i < n; i++) {int leftMax = 0;int rightMax = 0;for (int j = i; j >= 0; j--) leftMax = Math.max(leftMax, height[j]);for (int j = i; j < n; j++) rightMax = Math.max(rightMax, height[j]);ans += Math.min(leftMax, rightMax) - height[i];}return ans;}
}
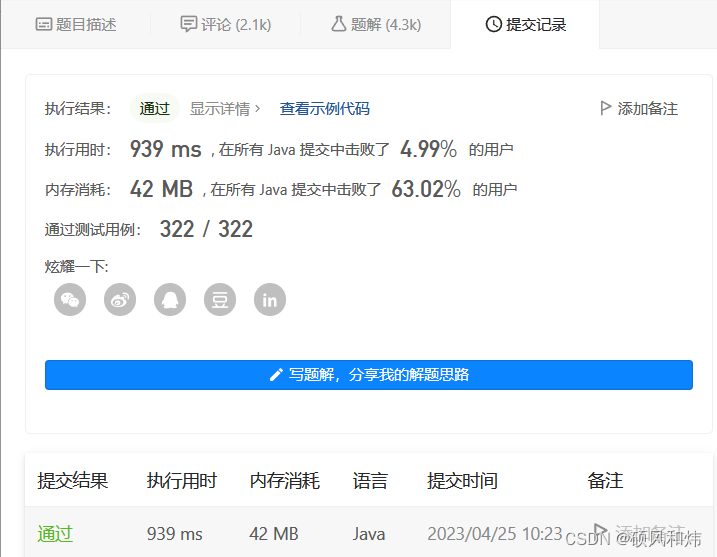
🥦 运行结果
时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
⚡ 动态规划
🥦 求解思路
我们可以使用动态规划来优化暴力法。首先预处理出每个位置左侧的最大高度和右侧的最大高度,分别存储在数组 l e f t M a x leftMax leftMax 和 r i g h t M a x rightMax rightMax 中。然后对于每个位置,计算其储水量 m i n ( l e f t M a x [ i ] , r i g h t M a x [ i ] ) − h e i g h t [ i ] min(leftMax[i], rightMax[i]) - height[i] min(leftMax[i],rightMax[i])−height[i],将所有储水量累加起来即可。
🥦 实现代码
class Solution {public int trap(int[] height) {int n=height.length;int[] leftMax=new int[n];int[] rightMax=new int[n];leftMax[0]=height[0];rightMax[n-1]=height[n-1];for(int i=1;i<n;i++) leftMax[i]=Math.max(leftMax[i-1],height[i]);for(int i=n-2;i>=0;i--) rightMax[i]=Math.max(rightMax[i+1],height[i]);int ans=0;for(int i=0;i<n;i++) ans+=Math.min(leftMax[i],rightMax[i])-height[i];return ans;}
}
🥦 运行结果
时间复杂度为 O ( n ) O(n) O(n)。

⚡ 单调栈
🥦 求解思路
使用单调栈来优化动态规划。我们使用栈来维护一个递减的柱子高度序列。具体地,遍历到第 i i i 个柱子时,如果当前柱子的高度 h e i g h t [ i ] height[i] height[i] 小于栈顶柱子的高度,则将当前柱子入栈;否则,不断从栈中弹出元素,直到栈为空或者当前栈顶元素的高度大于 h e i g h t [ i ] height[i] height[i],然后将当前柱子入栈。弹出元素时,我们可以计算其储水量,并将其累加到答案中。
🥦 实现代码
class Solution {public int trap(int[] height) {int n = height.length;Stack<Integer> stack = new Stack<>();int ans = 0;for (int i = 0; i < n; i++) {while (!stack.isEmpty() && height[i] > height[stack.peek()]) {int top = stack.pop();if (stack.isEmpty()) {break;}int left = stack.peek();int width = i - left - 1;int heightDiff = Math.min(height[left], height[i]) - height[top];ans += width * heightDiff;}stack.push(i);}return ans;}
}
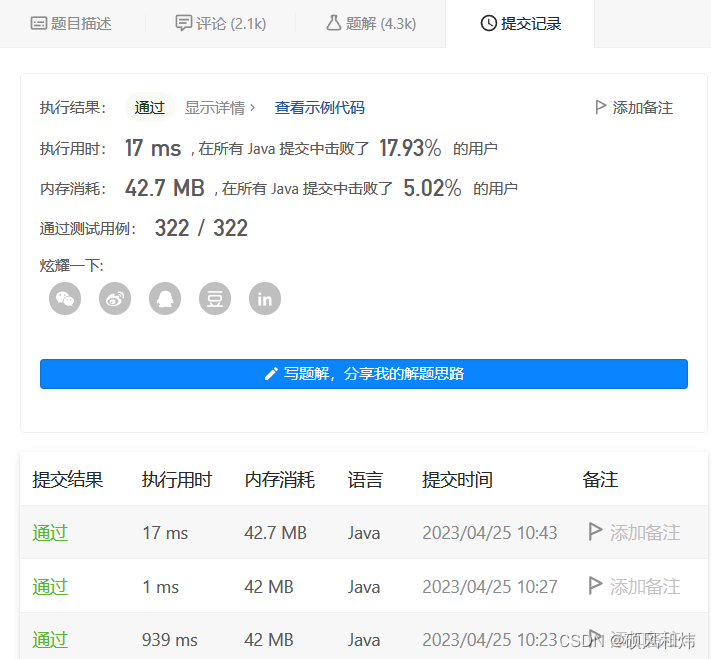
🥦 运行结果
时间复杂度为 O ( n ) O(n) O(n)。
🍋 总结
本文介绍了三种解法来解决 LeetCode 42 题,即接雨水问题。暴力法时间复杂度较高,使用动态规划和单调栈可以优化其效率。动态规划和单调栈的时间复杂度均为 O ( n ) O(n) O(n)。在实际应用中,可以根据具体情况来选择最合适的方法。
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【别再困扰于LeetCode接雨水问题了 | 从暴力法=>动态规划=>单调栈】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
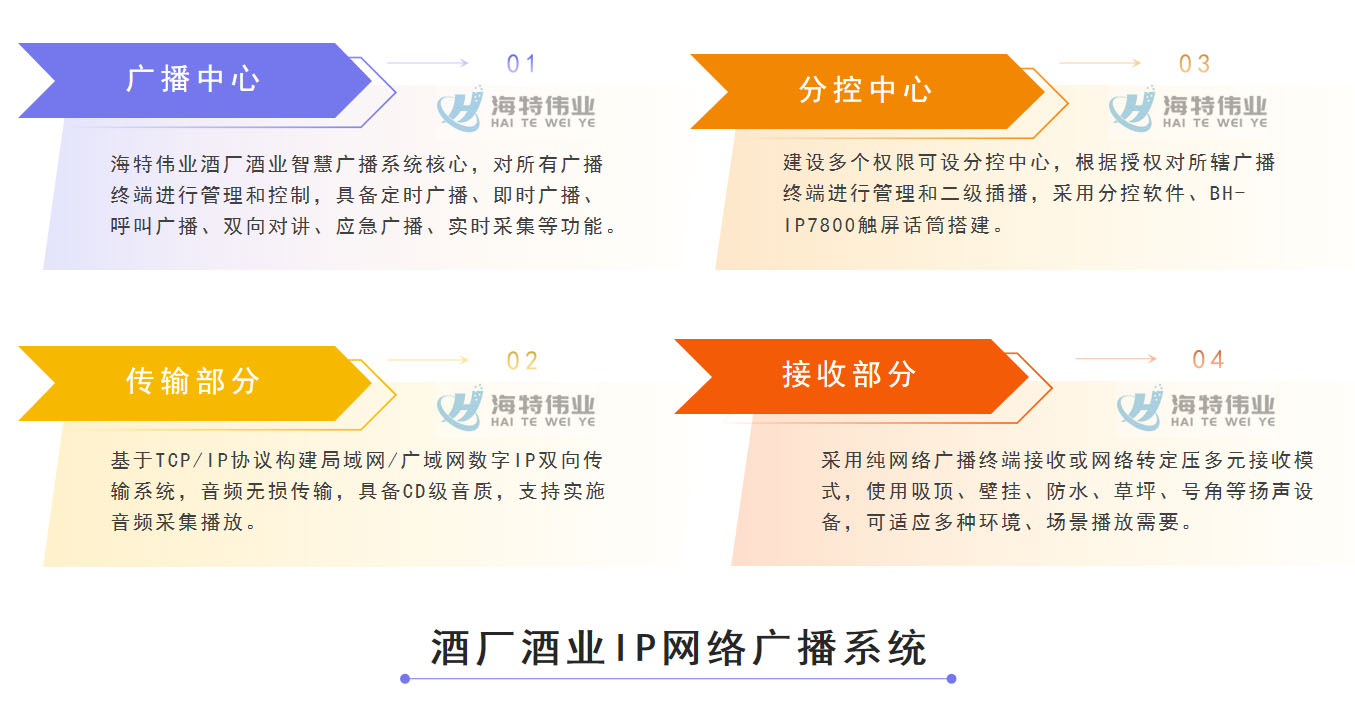
酒厂酒业IP网络广播系统建设方案-基于局域网的新一代交互智慧酒厂酒业IP广播设计指南
酒厂酒业IP网络广播系统建设方案-基于局域网的新一代交互智酒业酒厂IP广播系统设计指南 由北京海特伟业任洪卓发布于2023年4月25日 一、酒厂酒业IP网络广播系统建设需求 随着中国经济的快速稳步发展,中国白酒行业也迎来了黄金时期,产品规模、销售业绩等…...

OpenHarmony JS Demo开发讲解
项目结构 打开entry→src→main→js,工程的开发目录如图所示 其中, i18n文件夹:用于存放配置不同语言场景的资源,比如应用文本词条,图片路径等资源。en-US.json文件定义了在英文模式下页面显示的变量内容,…...
CentOS系统安装Intel E810 25G网卡驱动
因特尔网卡驱动给的都是二进制包,需要编译环境。 首先去Intel下载最新的驱动 E810驱动下载:https://www.intel.com/content/www/us/en/download/19630/intel-network-adapter-driver-for-e810-series-devices-under-linux.html?wapkwe810 里面有三个驱…...

Java经典的String面试题
Java经典的Spring面试题 String是基本数据类型吗? String你是基本数据类型String是可变的话? String是final类型的,不可变怎么比较两个字符串的值一样,怎么比较两个字符串是否同一对象? 比较字符串的值是否相同用equa…...

c# 结构体与类区别
在 C# 中,结构体(struct)和类(class)都是用户自定义类型,它们具有一些共同的特性,比如可以定义字段、属性、方法等。但它们也有一些区别。 下面是一些结构体和类的区别: 定义方式不…...

使用 patch 命令打补丁
之前的这篇文章 git 导出差异 diff 文件 写了导出 diff 、patch 文件。 拿到 patch 文件,用 patch 命令可以快速的把修改内容合入,合入后在 git 上是已修改的状态,如需提交还要 add 、commit 。 patch 语法 patch --help 可以看到 Usage:…...

C++——类和对象[上]
目录 1.初识面向对象 2.类的引入 3.类的定义 4.成员变量的命名规则 5.类的实例化 6.类对象模型 7.this指针 1.初识面向对象 C语言是一门面向过程的语言,它关注的是完成任务所需要的过程;C是一门面向对象的语言,将一个任务分为多个对…...
MySQL日志
目录 一 关于mysql的设计和运行逻辑 二 MySQL的三类日志 三 对于日志的利用 插入查询 1 备份 2 删除重复数据 一 关于mysql的设计和运行逻辑 mysql在启动的时候非常占空间,需要申请很大的空间,但是有时候内存并没有那么多,所以OS会把my…...

TinyURL 的加密与解密、猜数字游戏、 Fizz Buzz、相对名次----2023/4/28
TinyURL 的加密与解密----2023/4/28 TinyURL 是一种 URL 简化服务, 比如:当你输入一个 URL https://leetcode.com/problems/design-tinyurl 时,它将返回一个简化的URL http://tinyurl.com/4e9iAk 。请你设计一个类来加密与解密 TinyURL 。 加…...
Spring boot结合SkyWalking-Trace工具类实现日志打印请求链路traceid
背景: 随着业务的复杂化、解耦化,运维人员和开发人员需要对请求链路跟踪来快速发现和定位问题,基于应用已经集成了SkyWalking的前提下,如何通过获取SkyWalking生成的统一traceId并加入打印日志中,方便开发人员能够根据…...

精通ES=ElasticSearch
Elasticsearch 是一个分布式、高扩展、高实时的搜索与 数据分析引擎。它能很方便的使大量数据具有搜索、分析和探索的能力。充分利用Elasticsearch的水平 伸缩性,能使数据在 生产环境变得更有价值。Elasticsearch 的实现原理主要分为以下几个步骤,首先用…...
)
RabbitMQ-扇形交换机(Fanout )
扇形交换机:Fanout Exchange扇形交换机是最基本的交换机类型,它所能做的事情非常简单———广播消息。扇形交换机会把能接收到的消息全部发送给绑定在自己身上的队列。因为广播不需要“思考”,所以扇形交换机处理消息的速度也是所有的交换机类…...

Python 学习曲线 从 Python 新手到 Pro
Python 学习曲线 从 Python新手到 Pro 使用代码片段介绍: Python 是世界上最通用和使用最广泛的编程语言之一,以其简单性、可读性和多功能性而闻名。 在本文中,我们将探讨一系列示例场景,其中代码由具有三个不同专业知识水平的程序…...

薪资18K需要什么水平?来看看98年测试工程师的面试全过程…
我的情况 大概介绍一下个人情况,男,本科,三年多测试工作经验,懂python,会写脚本,会selenium,会性能,然而到今天都没有收到一份offer!从年后就开始准备简历,年…...

基于趋动云的 Stable Diffusion Webui 环境搭建
Stable Diffusion Webui 环境搭建,首先新建一个项目: 然后,选择镜像。注意点公开的,已近做好的这个镜像,superx创建,集成了miniconda3的镜像。 然后选择添加数据源,一样,还是点公开&…...

备忘录设计模式解读
目录 问题引进 游戏角色状态恢复问题 传统方案解决游戏角色恢复 传统的方式的问题分析 备忘录模式基本介绍 基本介绍 备忘录模式的原理类图 对原理类图的说明 游戏角色恢复状态实例 应用实例要求 思路分析和图解(类图) 代码实战 备忘录模式的注意事项和细节 问题引…...

股票期货模拟交易有用吗?股票期货模拟交易心得
股票期货市场为了满足新用户的需求,有专门的股票期货模拟交易平台,大家可以在这个平台上进行股票期货的模拟交易,这样可以通过不断总结,丰富我们的知识。下面整理的股票期货模拟交易实验心得,从股票期货模拟交易与实盘…...
2023年五月份图形化三级打卡试题
活动时间 从2023年5月1日至5月21日,每天一道编程题。 本次打卡的规则如下: 小朋友每天利用10~15分钟做一道编程题,遇到问题就来群内讨论,我来给大家答疑。 小朋友做完题目后,截图到朋友圈打卡并把打卡的截图发到活动群…...
100%通过率 详细代码注释)
【华为OD机试真题】字母组合(javapython)100%通过率 详细代码注释
字母组合 知识点回溯 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 每个数字对应多个字母,对应关系如下: 0: a,b,c 1: d,e,f 2: g,hi 3: j,k,l 4: m,n,o 5: p,q,r 6: s,t 7:u,v 8: w,x 9: y,z 输入一串数字后,通过数字和字母的对应关系可以得到多个字母字符串 (要…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
