多臂老虎机问题
1.问题简介
多臂老虎机问题可以被看作简化版的强化学习问题,算是最简单的“和环境交互中的学习”的一种形式,不存在状态信息,只有动作和奖励。多臂老虎机中的探索与利用(exploration vs. exploitation)问题一直以来都是一个特别经典的问题,理解它能够帮助我们学习强化学习。
2.问题介绍
2.1问题定义
在多臂老虎机(multi-armed bandit,MAB)问题中,有一个拥有 K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励的概率分布R。我们每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励 。我们在各根拉杆的奖励概率分布未知的情况下,从头开始尝试,目标是在操作 T次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的,因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。

2.2形式化描述
多臂老虎机问题可以表示为一个元组,其中:
- A为动作集合,其中一个动作表示拉动一个拉杆。若多臂老虎机一共有K根拉杆,那动作空间就是集合
,我们用
表示任意一个动作;
- R为奖励概率分布,拉动每一根拉杆的动作a都对应一个奖励概率分布R(r|a),拉动不同拉杆的奖励分布通常是不同的。
假设每个时间步只能拉动一个拉杆,多臂老虎机的目标为最大化一段时间步T内累积的奖励:
其中表示在第t时间步拉动某一拉杆的动作,
表示动作
获得的奖励。
对于每一个动作a,定义其期望奖励为:
![]()
于是,至少存在一根拉杆,它的期望奖励不小于拉动其他任意一根拉杆,我们将该最优期望奖励表示为:
![]()
懊悔(regret)定义为拉动当前拉杆的动作a与最优拉杆的期望奖励差,即 :
累积懊悔(cumulative regret)即操作 T次拉杆后累积的懊悔总量,对于一次完整的T步决策,累积懊悔为 :
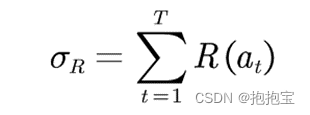
MAB 问题的目标为最大化累积奖励,等价于最小化累积懊悔。
为了知道拉动哪一根拉杆能获得更高的奖励,我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性,所以需要多次拉动一根拉杆,然后计算得到的多次奖励的期望,其算法流程如下所示:

以上 for 循环中的第四步如此更新估值,是因为这样可以进行增量式的期望更新,为什么不按照常规方法将所有数求和再除以次数呢?具体原因如下:
因为如果将所有数求和再除以次数,其缺点是每次更新的时间复杂度和空间复杂度均为 O(n)。而采用增量式更新,时间复杂度和空间复杂度均为O(1) 。
3. 代码实现
以下代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布(Bernoulli distribution),即每次拉下拉杆有P的概率获得的奖励为 1,有1-P的概率获得的奖励为 0。奖励为 1 代表获奖,奖励为 0 代表没有获奖。
# 导入需要使用的库,其中numpy是支持数组和矩阵运算的科学计算库,而matplotlib是绘图库
import numpy as np
import matplotlib.pyplot as pltclass BernoulliBandit:""" 伯努利多臂老虎机,输入K表示拉杆个数 """def __init__(self, K):self.probs = np.random.uniform(size=K) # 随机生成K个0~1的数,作为拉动每根拉杆的获奖# 概率self.best_idx = np.argmax(self.probs) # 获奖概率最大的拉杆self.best_prob = self.probs[self.best_idx] # 最大的获奖概率self.K = Kdef step(self, k):# 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1(获奖)或0(未# 获奖)if np.random.rand() < self.probs[k]:return 1else:return 0np.random.seed(1) # 设定随机种子,使实验具有可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print("随机生成了一个%d臂伯努利老虎机" % K)
print("获奖概率最大的拉杆为%d号,其获奖概率为%.4f" %(bandit_10_arm.best_idx, bandit_10_arm.best_prob))接下来我们用一个 Solver 基础类来实现上述的多臂老虎机的求解方案。需要实现下列函数功能:根据策略选择动作、根据动作获取奖励、更新期望奖励估值、更新累积懊悔和计数。在下面的 MAB 算法基本框架中,我们将根据策略选择动作、根据动作获取奖励和更新期望奖励估值放在 run_one_step() 函数中,由每个继承 Solver 类的策略具体实现。而更新累积懊悔和计数则直接放在主循环 run() 中。
class Solver:""" 多臂老虎机算法基本框架 """def __init__(self, bandit):self.bandit = banditself.counts = np.zeros(self.bandit.K) # 每根拉杆的尝试次数self.regret = 0. # 当前步的累积懊悔self.actions = [] # 维护一个列表,记录每一步的动作self.regrets = [] # 维护一个列表,记录每一步的累积懊悔def update_regret(self, k):# 计算累积懊悔并保存,k为本次动作选择的拉杆的编号self.regret += self.bandit.best_prob - self.bandit.probs[k]self.regrets.append(self.regret)def run_one_step(self):# 返回当前动作选择哪一根拉杆,由每个具体的策略实现raise NotImplementedErrordef run(self, num_steps):# 运行一定次数,num_steps为总运行次数for _ in range(num_steps):k = self.run_one_step()self.counts[k] += 1self.actions.append(k)self.update_regret(k)相关文章:

多臂老虎机问题
1.问题简介 多臂老虎机问题可以被看作简化版的强化学习问题,算是最简单的“和环境交互中的学习”的一种形式,不存在状态信息,只有动作和奖励。多臂老虎机中的探索与利用(exploration vs. exploitation)问题一直以来都…...

DNS 查询原理详解
DNS(Domain Name System)是互联网上的一种命名系统,它将域名转换为IP地址。在进行DNS查询时,先要明确需要查询的主机名,然后向本地DNS服务器发出查询请求。 1. 本地DNS服务器查询 当用户在浏览器中输入一个URL或者点…...
浅谈软件测试工程师的技能树
软件测试工程师是一个历史很悠久的职位,可以说从有软件开发这个行业以来,就开始有了软件测试工程师的角色。随着时代的发展,软件测试工程师的角色和职责也在悄然发生着变化,从一开始单纯的在瀑布式开发流程中担任测试阶段的执行者…...

转型产业互联网,新氧能否再造辉煌?
近年来,“颜值经济”推动医美行业快速发展,在利润驱动下,除了专注医美赛道的企业之外,也有不少第三方互联网平台正强势进入医美领域,使以新氧为代表的医美企业面对不小发展压力,同时也展现出强大的发展韧性…...
CRE66365 应用资料
CRE66365是一款高度集成的电流模式PWM控制IC,为高性能、低待机功耗和低成本的隔离型反激转换器。在正常负载条件下,AC输入高电压下工作在QR模式。为了最大限度地减少开关损耗,QR 模式下的最大开关频率被内部限制为 77kHz。当负载较低时&#…...
vue3快速上手学习笔记,还不快来看看?
Vue3快速上手 1.Vue3简介 2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王)耗时2年多、2600次提交、30个RFC、600次PR、99位贡献者github上的tags地址:https://github.com/vuejs/vue-next/release…...

HDU 5927 Auxiliary Set
原题链接: https://acm.hdu.edu.cn/showproblem.php?pid5927 题意: 有一颗根节点是1的树,其中有重要的点和不重要的点,重要的点需满足以下两个条件至少一个: 1.本来就是重要的点 2.是两个重要的点的最近共同祖先 有t…...

24:若所有参数皆需类型转换,请为此采用non-member函数
令class支持隐式类型转换通常是个糟糕的主意。 这条规则有其例外,最常见的例外是在建立数值类型时。 例,假设你设计一个class用来表现有理数,则允许整数“隐式转换”为有理数就很合理。 class Rational{ public:Rational(int numerator0,i…...
-详解-编译-安装-支持GDB-添加环境检查-添加版本号-生成安装包)
CMake(2)-详解-编译-安装-支持GDB-添加环境检查-添加版本号-生成安装包
目录 1.什么是CMake 1.1 编译流程CMakeLists.txt a) 最简单 demo1 b) 常用demo2 c) 单目录,源文件-输出文件 DIR_SRCS中 d)多目录,多源文件 1.2.执行命令: 1.3.自定义编译选项 2.安装和测试 3.支持GDB 4.添加环境检查 5.添加…...
)
java面试题(redis)
目录 1.redis主要消耗什么物理资源? 2.单线程为什么快 3.为什么要使用Redis 4.简述redis事务实现 5.redis缓存读写策略 6.redis除了做缓存,还能做些什么? 7.redis主从复制的原理 8.Redis有哪些数据结构?分别有哪些典型的应…...

Vue组件懒加载
组件懒加载 前言 组件懒加载最常用于异步加载大型/复杂组件或在需要时才进行加载 Vue 2和Vue 3均支持组件懒加载,本文将介绍如何在Vue 2和Vue 3中实现组件懒加载,和一些使用场景 1️⃣方法一:使用Webpack的代码分割能力 Vue 2和Vue 3都可以…...

Qt音视频开发42-网络推流(视频推流/本地摄像头推流/桌面推流/网络摄像头转发推流等)
一、前言 上次实现的文件推流,尽管优点很多,但是只能对现在存在的生成好的音视频文件推流,而现在更多的场景是需要将实时的视频流重新推流分发,用户在很多设备比如手机/平板/网页/电脑/服务器上观看,这样就可以很方便…...

更简单的存取Bean方式-@Bean方法注解
1.Bean方法存储 类注解是添加在某个类上的,那么方法注解是添加在某个方法前的 public class UserBeans {Beanpublic User user1(){User user new User();user.setUid(001);user.setUname("zhangsan");user.setAge(19);user.setPassword("123123");retur…...

边缘计算与AI布署应用电力物联网解决方案-RK3588开发平台
电力行业拥有规模庞大的各类设备,如电表、各类保护、采集、控制设备。面对分布式发电、储能、用户微网等一系列综合问题,边缘计算与AI布署可满足“端侧本地化”高效运用的需求,协助提升最后一公里运行效率。 瑞芯微RK3588J、内置独立NPU&…...

centos部署unity accelerator
参考 https://docs.unity3d.com/Manual/UnityAccelerator.html 方案1:下载Unity Accelerator 手动安装, unity-accelerator-app-v1.0.941g6b39b61.AppImage为下载的文件 1、放入服务器目录, chmod x unity-accelerator-app-v1.0.941g6b39b61.AppImage 2…...

HANA开发指南
建模方面 1、建模方式:图像化建模、SQL建模、CE语言建模 2、维护:SQL和CE比图形化建模更容易维护和修改 3、性能:图形化和CE会经过系统优化,性能一般优于SQL语言 4、可按需要设置参数、变量、Hierachy、聚合类型等 5、在S4系…...
请问你见过吐代码的泡泡吗(冒泡排序)
🤩本文作者:大家好,我是paperjie,感谢你阅读本文,欢迎一建三连哦。 🥰内容专栏:这里是《算法详解》,笔者用重金(时间和精力)打造,将算法知识一网打尽,希望可以…...
【VM服务管家】VM4.0平台SDK_2.1环境配置类
目录 2.1.1 环境配置:CSharp二次开发环境配置方法2.1.2 环境配置:Qt二次开发环境配置方法2.1.3 环境配置:MFC二次开发环境配置方法2.1.4 环境配置:VB.Net二次开发环境配置方法2.1.5 环境配置:运行出现Vm.Core.Solution…...
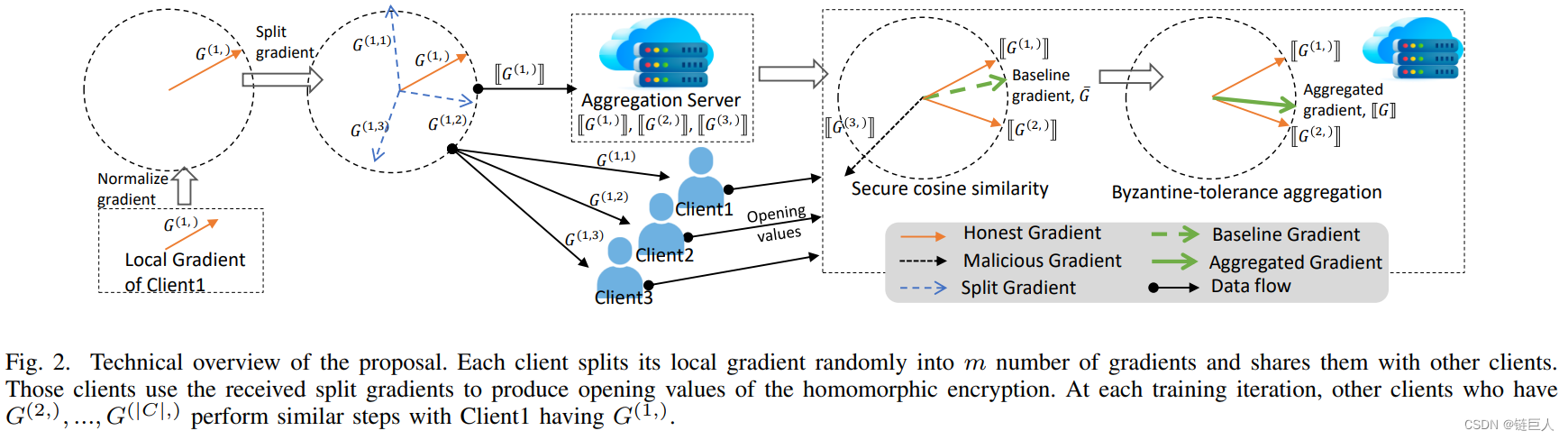
最新研究:可审计的具有拜占庭鲁棒的联邦学习方案
Y. Liang, Y. Li and B. -S. Shin, “Auditable Federated Learning With Byzantine Robustness,” in IEEE Transactions on Computational Social Systems, doi: 10.1109/TCSS.2023.3266019. 可免费下载:https://download.csdn.net/download/liangyihuai/87727720…...

JDK1.8下载、安装和环境配置教程
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🦾🦾 目录 window系统安装java 下载JDK 配置环境变量 …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
