剑指 Offer第二版:1~n 整数中 1 出现的次数、51. 数组中的逆序对、56 - II. 数组中数字出现的次数 II
剑指 Offer第二版
- 43. 1~n 整数中 1 出现的次数
- 51. 数组中的逆序对
- 56 - II. 数组中数字出现的次数 II
43. 1~n 整数中 1 出现的次数
题目:输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
输入:n = 12
输出:5
**思路分析:**将n的每一位数分别处理,计算出每个位数上1的个数,然后将所有位数上1的个数相加即可。具体来说,首先判断n是否为0,如果n为0,直接返回0。然后从低位到高位依次处理每一位数,计算当前位数上1的个数。如果当前位数的数字小于1,1的个数为高位数当前位数,即highbit;如果当前位数的数字等于1,1的个数为高位数当前位数+低位数+1,即highbit+low+1;如果当前位数的数字大于1,1的个数为(high+1)*bit,即高位数加一乘以当前位数。最后将所有位数上1的个数相加即为最终结果。
时间复杂度:需要处理n的每一位数,因此时间复杂度为 O ( log n ) O(\log n) O(logn)。
空间复杂度:只需要使用常量级别的额外空间,因此空间复杂度为 O ( 1 ) O(1) O(1)。
class Solution {public int countDigitOne(int n) {if (n == 0) { // 如果n为0,直接返回0return 0;}long bit = 1; // bit表示当前处理的位数long cur = n / bit % 10; // cur表示当前处理的数字long low = n % bit; // low表示当前位数以下的数字long high = n / bit / 10; // high表示当前位数以上的数字long res = 0; // res表示1的个数while (bit <= n) { // 当位数小于等于n的位数时,继续处理if (cur < 1) { // 如果当前位数的数字小于1,1的个数为high*bitres += high * bit;} else if (cur == 1) { // 如果当前位数的数字等于1,1的个数为high*bit+low+1res += high * bit + low + 1;} else { // 如果当前位数的数字大于1,1的个数为(high+1)*bitres += (high + 1) * bit;}bit *= 10; // 处理下一位数cur = n / bit % 10;low = n % bit;high = n / bit / 10;}return (int) res; // 返回1的个数}
}51. 数组中的逆序对
题目:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
思路分析: 在归并排序的过程中,每次合并两个有序的子数组时,需要统计逆序对数量。具体实现时,在合并过程中,如果左半段的数大于等于右半段的数,则说明左半段中剩余的数都比右半段的数大,因此可以直接统计逆序对数量。
时间复杂度:归并排序的时间复杂度为O(nlogn),而在归并排序的过程中,每次合并两个有序的子数组时,需要遍历所有元素一次,因此合并的时间复杂度也是O(nlogn)。因此总的时间复杂度为O(nlogn)。
空间复杂度:归并排序需要使用一个临时数组来存储合并过程中的数据,因此空间复杂度为O(n)。
class Solution {int res = 0; // 记录逆序对数量public int reversePairs(int[] nums) {if (nums == null || nums.length == 0) {return 0;}mergeSort(nums, 0, nums.length - 1); // 归并排序return res; // 返回逆序对数量}private void mergeSort(int[] nums, int l, int r) {if (l >= r) {return;}int mid = (r - l) / 2 + l; // 计算中间位置mergeSort(nums, l, mid); // 对左半段进行归并排序mergeSort(nums, mid + 1, r); // 对右半段进行归并排序merge(nums, l, mid, r); // 合并左右两个有序的子数组}private void merge(int[] nums, int l, int mid, int r) {int i = l; // 左半段的起始位置int j = mid + 1; // 右半段的起始位置int[] temp = new int[r - l + 1]; // 用于存储合并过程中的数据int index = 0; // 临时数组的下标while (i <= mid && j <= r) { // 合并左右两个有序的子数组if (nums[i] <= nums[j]) { // 如果左半段的数小于右半段的数temp[index++] = nums[i++]; // 将左半段的数加入临时数组中} else { // 如果左半段的数大于等于右半段的数res += mid - i + 1; // 统计逆序对数量temp[index++] = nums[j++]; // 将右半段的数加入临时数组中}}// 将剩余的元素复制到临时数组中while (i <= mid) {temp[index++] = nums[i++];}while (j <= r) {temp[index++] = nums[j++];}// 将临时数组中的元素复制回原数组中index = 0;for (i = l; i <= r; i++) {nums[i] = temp[index++];}}
}
56 - II. 数组中数字出现的次数 II
题目:在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
示例 1:
输入:nums = [3,4,3,3]
输出:4
思路分析: 对于每一位,统计所有数字在该位上出现的次数,然后对3取模,得到出现1次的数字在该位上的值。最后将所有位的值合并起来,即得到最终结果。
时间复杂度为O(nk),其中n为数字数量,k为数字的二进制位数,因为需要遍历所有数字和所有位数。
空间复杂度为O(k),因为需要使用一个长度为k的数组来记录每个数字在每个位上出现的次数。
class Solution {public int singleNumber(int[] nums) {if(nums == null || nums.length == 0){return -1;}int res = 0; // 用于存储最终结果int bit = 1; // 用于表示当前位的值,从最低位开始int[] count = new int[32]; // 用于记录所有数字在当前位上出现的次数for(int i = 0; i < 32; i++){ // 遍历所有位for(int j = 0; j < nums.length; j++){ // 遍历所有数字if((nums[j] & bit) != 0){ // 如果当前数字在当前位上为1count[i]++; // 记录出现次数}}count[i] %= 3; // 对3取模,得到出现1次的数字在当前位上的值res += bit * count[i]; // 将当前位的值加入最终结果bit <<= 1; // 判断下一位}return res; // 返回最终结果}
}
相关文章:

剑指 Offer第二版:1~n 整数中 1 出现的次数、51. 数组中的逆序对、56 - II. 数组中数字出现的次数 II
剑指 Offer第二版 43. 1~n 整数中 1 出现的次数51. 数组中的逆序对56 - II. 数组中数字出现的次数 II 43. 1~n 整数中 1 出现的次数 题目:输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。 例如,…...
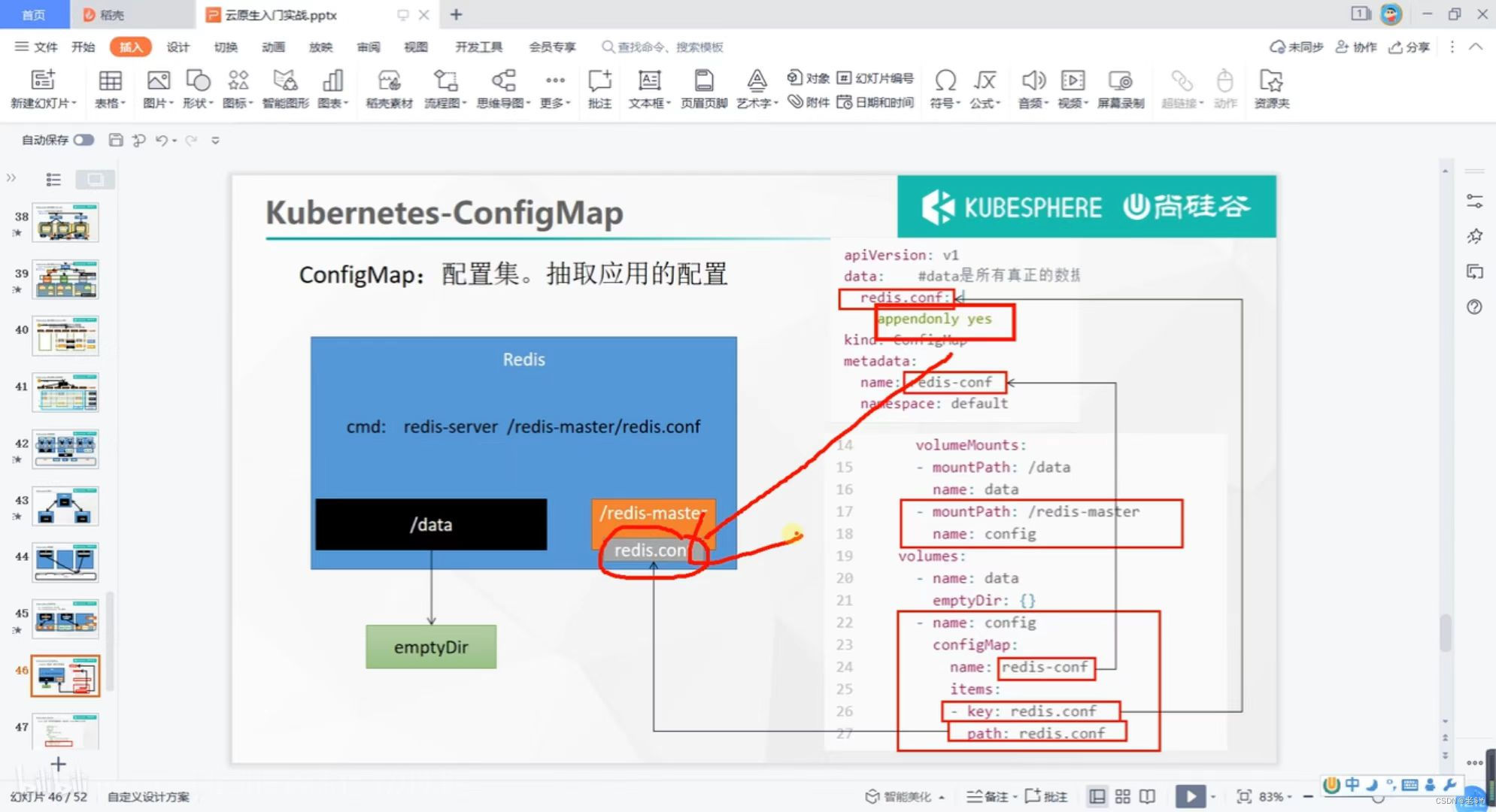
云原生-k8s核心概念(pod,deploy,service,ingress,configmap,volume)
Gitee-k8s学习 云原生实战-kubernetes核心实战 namespace Namespace是kubernetes系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离 Pod Pod可以认为是容器的封装,一个Pod中可以存在一个或者多个容器。 De…...

他工作10年,老板却让他走人
大家好,我是五月,一个编程街溜子。 二狗被裁了,他在公司待了快十年,他想留下来,老板却让他走。 我和他一样困惑。 他985毕业,工作中有从0开始一个项目直到日活过千万,也有过参与顶级产品核心…...

vpp怎么写node
VPP(Vector Packet Processing)是一个高性能的数据平面开源项目,用于构建网络功能虚拟化(NFV)和软件定义网络(SDN)解决方案。它由Cisco开发,并在Apache 2.0许可下发布。 在VPP中&am…...
【4. ROS的主要通讯方式:Topic话题与Message消息】
【4. ROS的主要通讯方式:Topic话题与Message消息】 1. 前言1.1 王者解释结点通讯:1.2 通讯小结 2. 灵活的Topic话题图解2.1 话题注意细节2.2 外延补充 3. Message消息图解3.1 消息类型3.2 查看标准消息类型std_msgs 4. 使用C实现Publisher发布者4.1 发布…...

【react全家桶学习】react中组件定义及state属性(超详/必看)
函数式组件定义及特点 定义(核心就是一个函数,返回虚拟dom): import React from reactexport default function index() {return <div>index</div> }特点: 1、适用于【简单组件】的定义2、是一个函数&a…...

如何以产品经理思维打造一所高品质学校?
学校的建设与管理真不是一件容易事。2023年03月17日,山东菏泽市曹县一家长投诉某中学课业繁重,孩子经常写作业到半夜;2023年4月4日,张先生在华龙网重庆网络问政平台投诉万州区某中学伙食差,指出“发灰的洋葱࿰…...

根治Spring中使用Mongo时报错InvalidMongoDbApiUsageException
文章目录 And Or迷惑原因 告别InvalidMongoDbApiUsageException问题简单解决根本解决修改源码 代码(省流,可以直接看这里) And Or 很多时候都需要进行逻辑的与或操作,但是spring当中自带的操作并不好用,于是做了相关的改进&#…...

【计算机组成原理】数据的表示和运算·进位计数制
🚩 本文已收录至专栏:计算机基础 我们可以通过显示屏看到各种形式的数据信息,但数据是如何在计算机中表示呢?运算器又是如何实现数据的算数、逻辑运算? 十进制数是最适合我们日常使用的一种计数方式,除此之…...
)
C++ Primer第五版_第十四章习题答案(21~30)
文章目录 练习14.21练习14.22头文件CPP文件 练习14.23头文件CPP文件 练习14.24头文件CPP文件 练习14.25练习14.26练习14.27练习14.28练习14.29练习14.30 练习14.21 编写 Sales_data 类的 和 运算符,使得 执行实际的加法操作而 调用。相比14.3节和14.4节对这两个运…...

服务器性能调优
硬件 如果是硬件瓶颈就换硬件 (包括CPU、内存、网卡) 软件 如果是方案架构设计有问题就换方案,比如mysql、redis方案有问题 建议先 top 看下软件瓶颈在哪,CPU、内存、网络(netstat),哪个进程占…...
带你深入学习k8s--(三) pod 管理
目录 一、简介 1、什么是pod 2、为什么要有pod 二、pod的分类 0、pod常用命令命令 1、准备镜像 2、自主式pod 3、控制器创建pod 4、扩容pod数量 5、通过service暴露pod(负载均衡,自动发起) 6、更新应用版本 三、编写yaml文件 四、Pod生命周期…...

前端系列11集-ES6 知识总结
ES Module 优点 静态分析 浏览器和 Node 都支持 浏览器的新 API 能用模块格式提供 不再需要对象作为命名空间 export 用于规定模块的对外接口 输出的接口与其对应的值是动态绑定关系可以取到模块内部实时的值 import 用于输入其他模块提供的功能 具有提升效果,会提升…...

连接分析工具箱 | 利用CATO进行结构和功能连接重建
导读 本研究描述了一个连接分析工具箱(CATO),用于基于扩散加权成像(DWI)和静息态功能磁共振成像(rs-fMRI)数据来重建大脑结构和功能连接。CATO是一个多模态软件包,使研究人员能够运行从MRI数据到结构和功能连接组图的端到端重建,定制其分析并…...

【目标检测论文阅读笔记】Detection of plane in remote sensing images using super-resolution
Abstract 由于大量的小目标、实例级噪声和云遮挡等因素,遥感图像的目标检测精度低,漏检率或误检率高。本文提出了一种新的基于SRGAN和YOLOV3的目标检测模型,称为SR-YOLO。解决了SRGAN网络 对超参数的敏感性和模态崩溃问题。同时,Y…...

外卖app开发流程全解析
外卖app开发是现代餐饮业的一个必备部分。在这个数字化时代,人们更愿意使用手机应用程序来订购食品。因此,为了满足客户需求,餐饮企业需要开发自己的外卖app。 第一步:确定目标受众 在开始外卖app的开发之前,需要确定…...

BUUCTF jarvisoj_level0
小白垃圾做题笔记而已,不建议阅读。。。 这道题感觉主要就是64位程序ebp8 题目中给出了shellcode 我们直接将返回地址覆盖就好。 在main函数中调用了vulnerable_function()函数。 vulnerable函数是一个漏洞函数:(存在缓溢出),我们只需要将…...
网络安全之入侵检测
目录 网络安全之入侵检测 入侵检测经典理论 经典检测模型 入侵检测作用与原理 意义 异常检测模型(Anomaly Detection) 误用检测模型(Misuse Detection) 经典特征案例 编辑自定义签名 编辑 签名检查过程 检测生命周期…...

元数据管理
1、业务元数据 描述 ”数据”背后的业务含义主题定义:每段 ETL、表背后的归属业务主题。业务描述:每段代码实现的具体业务逻辑。标准指标:类似于 BI 中的语义层、数仓中的一致性事实;将分析中的指标进行规范化。标准维度…...
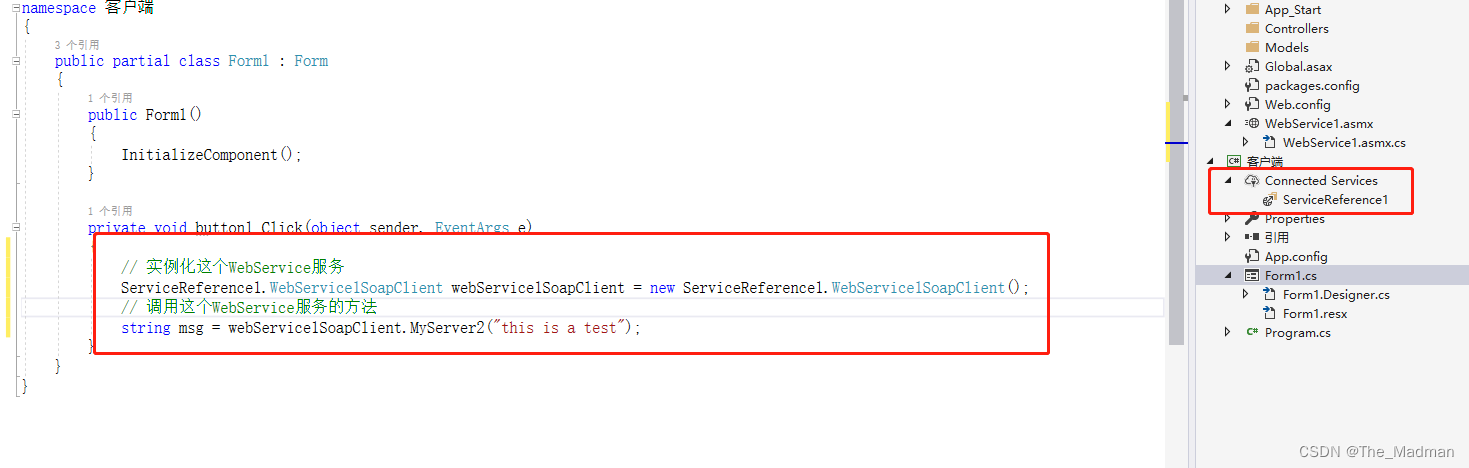
C# WebService的开发以及客户端调用
目录 1、WebService简介 1.1 什么是XML? 1.2 什么是Soap? 1.3 什么是WSDL? 2、WebService与WebApi的区别与优缺点 2.1 WebService与WebApi的区别: 2.2 WebService的优缺点: 2.3 WebApi的优缺点: 3…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
