二叉树及其遍历
文章目录
- 二叉树
- 树的定义
- 二叉树的定义
- 遍历
- 先序遍历
- 中序遍历
- 后序遍历
- 层次遍历
- 定义队列
- 层次创建二叉树
- 层次遍历
二叉树
树是一种非线性的数据结构,由若干个节点组成,节点之间存在一种父子关系,具有层次结构。二叉树是一种特殊的树结构,每个节点最多有两个子节点。树结构可以用来实现各种算法,例如二叉查找树、平衡二叉树、堆等。
树的定义
树(Tree) 是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:
- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可分为
m(m>0)个互不相交的有限集T1、T2、…、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
此外,树的定义还需要强调以下两点:
n>0时根结点是唯一的,不可能存在多个根结点,数据结构中的树只能有一个根结点。m>0时,子树的个数没有限制,但它们一定是互不相交的。
二叉树的定义
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
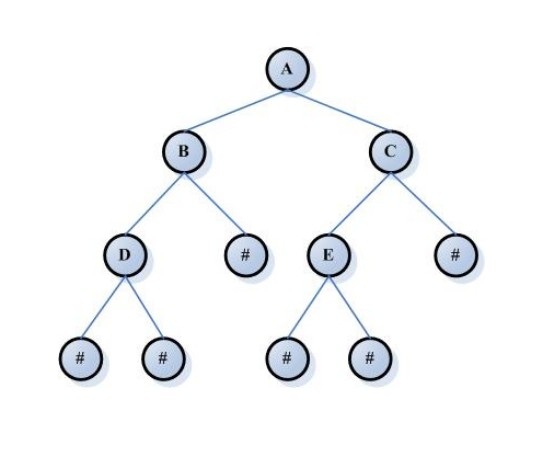
从定义和图例中可以看出,二叉树每个节点最多只会有两棵子树,且左右子树是有顺序的,次序不能随意颠倒。当一个节点既没有左子树也没有右子树,则该节点为叶子节点。
代码实现
结构体定义树
typedef struct Tree{int val; //数据域struct Tree *left; // 左子树struct Tree *right; // 右子树
}Tree,*tree;
遍历
二叉树作为一种存储结构,将数据存入之后,则需要遍历对数据进行对应的处理。而二叉树的遍历分为四种:先(前)序遍历、中序遍历、后序遍历、层次遍历。
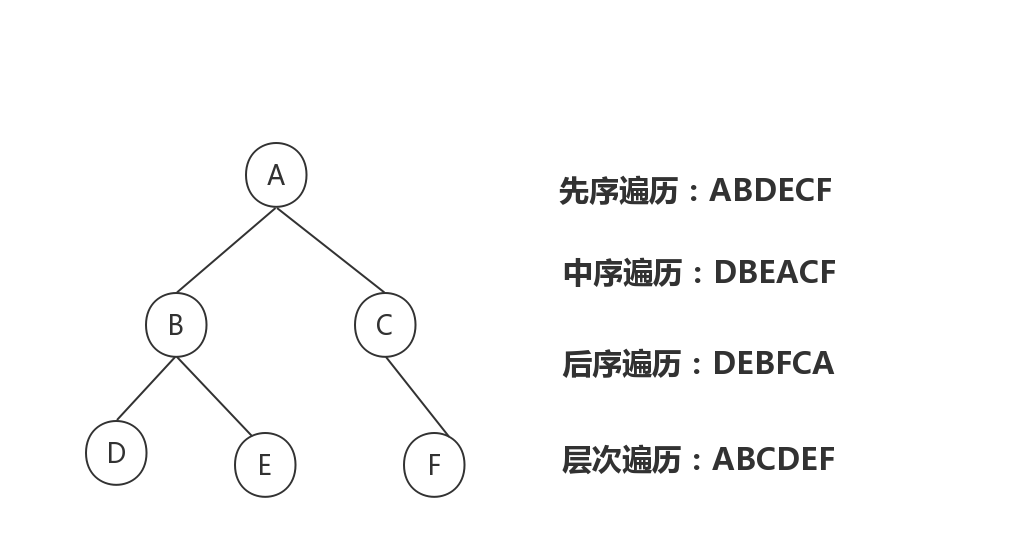
先序遍历
先序遍历是指从根节点开始,经过左子树,最后再遍历右子树,遍历顺序为:根节点->左子树->右子树。
代码实现
首先使用先序递归的创建一颗二叉树
// 创建新节点
Tree newNode(int val){Tree root = (Tree) malloc(sizeof (tree));root->val = val;root->left = NULL;root->right = NULL;return root
}
Tree CreateBiTree(int* len){//创建一颗节点数为len的二叉树if((*len)<=0){return NULL;}int val; //创建一个数据接收参数。printf("请输入插入数值:");// 为根节点数据域赋值scanf("%d",&val);//创建一个根节点Tree root = newNode(val);(*len)--;root->left = CreateBiTree(len); //递归创建左子树root->right = CreateBiTree(len); //递归创建右子树//创建完成后返回根节点return root;
}
再进行先序遍历
//先序遍历
void preorder(Tree root){if(root==NULL){return ;}// 首先输出根节点的值printf("节点的值:%d\n",root->val);//先递归遍历左子树preorder(root->left);//递归遍历右子树preorder(root->right);
}
运行结果
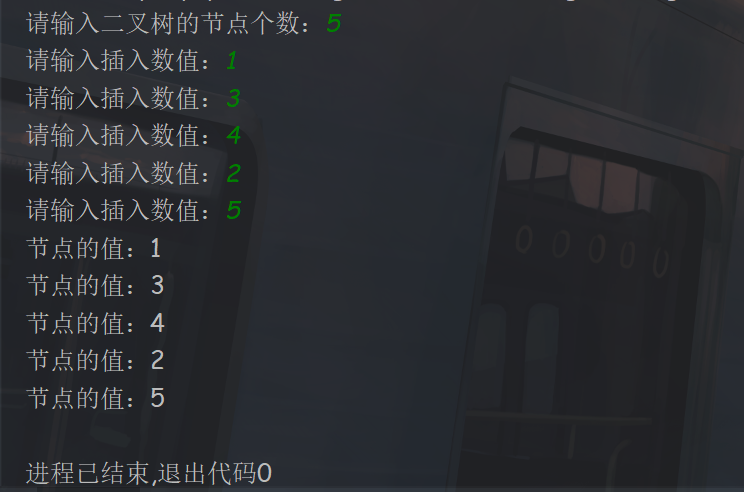
中序遍历
中序遍历是指从左子树开始,再访问根节点,最后遍历右子树,遍历顺序为:左子树->根节点->右子树。
代码实现
利用先序递归创建一颗二叉树,并使用中序遍历二叉树
//中序遍历
void inorder(Tree root){//如果节点为NULL,退出遍历if(root==NULL){return ;}//先递归遍历左子树inorder(root->left);// 输出根节点的值printf("节点的值:%d\n",root->val);//递归遍历右子树inorder(root->right);
}
运行结果
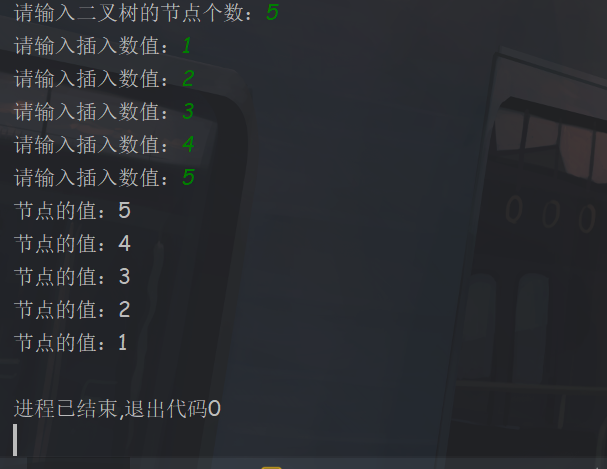
后序遍历
后序遍历是指从左子树开始,再遍历右子树,最后访问根节点,遍历顺序为:左子树->右子树->根节点。
代码实现
// 后序遍历
void postorder(Tree root){//如果节点为NULL,退出遍历if(root==NULL){return ;}//先递归遍历左子树postorder(root->left);//再递归遍历右子树postorder(root->right);//输出根节点的值printf("节点的值:%d\n",root->val);
}
运行结果
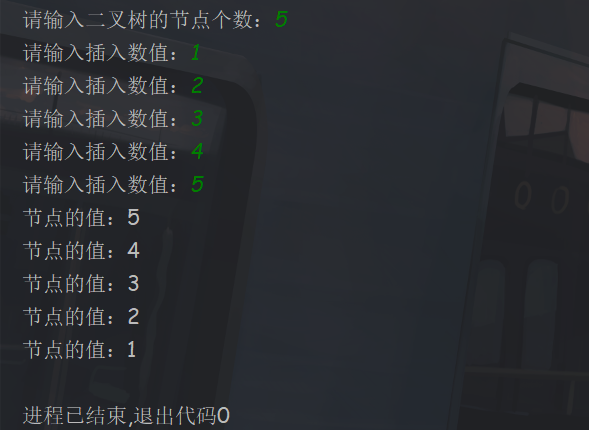
为什么后序遍历和中序遍历的结果相同呢?
因为创建二叉树的时候使用的是前序递归,所以创建出来的二叉树都在根节点的左子树上,其右子树为空,此时这种情况被称为斜二叉树,并且也被称之为二叉树退化成单链表。这样创建出来的二叉树是很浪费空间且不规范的。
所以先序递归创建的二叉树是不可取的。此时就用到层次创建二叉树,层次创建是用到最多的创建方式,也是较为直观的一种创建方式。
层次遍历
层次遍历是指从根节点开始,然后一层一层向下遍历。
代码实现
一把是利用队列来实现层次创建及遍历二叉树
定义队列
// 定义队列
struct Queue {struct Tree *Tree;struct Queue *next;
};// 初始化队列
void initQueue(struct Queue **head, struct Queue **tail) {*head = *tail = NULL;
}// 入队
void enQueue(struct Queue **head, struct Queue **tail, struct Tree *Tree) {struct Queue *node = (struct Queue*)malloc(sizeof(struct Queue));node->Tree = Tree;node->next = NULL;if (*head == NULL) {*head = *tail = node;} else {(*tail)->next = node;*tail = node;}
}// 出队
struct Tree* deQueue(struct Queue **head, struct Queue **tail) {if (*head == NULL) {return NULL;}struct Tree *Tree = (*head)->Tree;if (*head == *tail) {*head = *tail = NULL;} else {*head = (*head)->next;}return Tree;
}
层次创建二叉树
// 创建二叉树
struct Tree* createTree(int *arr, int size) { //arr为数据数组,size为层数if (size == 0) {return NULL;}// 创建根节点struct Tree *root = (struct Tree*)malloc(sizeof(struct Tree));root->val = arr[0];root->left = NULL;root->right = NULL;// 初始化队列struct Queue *head, *tail;initQueue(&head, &tail);enQueue(&head, &tail, root);int i = 1;// 层次遍历创建二叉树while (i < size) {struct Tree *node = deQueue(&head, &tail);// 左子树if (i < size && arr[i] != -1) { //当数据为-1时证明该处为空节点node->left = (struct Tree*)malloc(sizeof(struct Tree));node->left->val = arr[i];node->left->left = NULL;node->left->right = NULL;enQueue(&head, &tail, node->left);}i++;// 右子树if (i < size && arr[i] != -1) {node->right = (struct Tree*)malloc(sizeof(struct Tree));node->right->val = arr[i];node->right->left = NULL;node->right->right = NULL;enQueue(&head, &tail, node->right);}i++;}return root;
}
层次遍历
// 层次遍历
void levelOrder(struct Tree* root) {if (root == NULL) {return;}struct Queue *head, *tail; // 定义队头与队尾initQueue(&head, &tail);enQueue(&head, &tail, root);while (head != NULL) {struct Tree *node = deQueue(&head, &tail);printf("%d ", node->val);if (node->left != NULL) {enQueue(&head, &tail, node->left);}if (node->right != NULL) {enQueue(&head, &tail, node->right);}}
}
main函数
// 测试代码
int main() {// 层次遍历序列,其中-1表示空节点int arr[] = {1, 2, 3, 4, -1, -1, 5};int size = sizeof(arr) / sizeof(int);// 创建二叉树struct Tree* root = createTree(arr, size);// 打印二叉树levelOrder(root);return 0;
}
运行结果

层次遍历已经实现,接着使用层次创建二叉树,并实现先中后序遍历
运行结果分别为:
先序遍历

中序遍历

后序遍历

相关文章:

二叉树及其遍历
文章目录 二叉树树的定义二叉树的定义遍历先序遍历中序遍历后序遍历层次遍历定义队列层次创建二叉树层次遍历 二叉树 树是一种非线性的数据结构,由若干个节点组成,节点之间存在一种父子关系,具有层次结构。二叉树是一种特殊的树结构ÿ…...
java 版本企业电子招投标采购系统源码之登录页面
信息数智化招采系统 服务框架:Spring Cloud、Spring Boot2、Mybatis、OAuth2、Security 前端架构:VUE、Uniapp、Layui、Bootstrap、H5、CSS3 涉及技术:Eureka、Config、Zuul、OAuth2、Security、OSS、Turbine、Zipkin、Feign、Monitor、…...

第五章 使用RAID与LVM磁盘阵列技术
第五章 使用RAID与LVM磁盘阵列技术 一、RAID磁盘冗余阵列 1、部署磁盘阵列 (1)、RAID0、1、5、10方案技术对比 RAID级别最少硬盘可用容量读写性能安全性特点02nn低追求最大容量和速度,任何一块盘损坏,数据全部异常。12n/2n高追…...

LeetCode 560. 和为 K 的子数组
LeetCode 560. 和为 K 的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入:nums [1,2,3], k 3 …...

后端要一次性返回我10万条数据
问题描述 面试官:后端一次性返回10万条数据给你,你如何处理?我:歪嘴一笑,what the f**k! 问题考察点 看似无厘头的问题,实际上考查候选人知识的广度和深度,虽然在工作中这种情况很少遇到... …...

汽车智能化「出海」红利
在高阶智能座舱中,车载导航产品作为与用户体验息息相关的模块之一,同样也进入了升级迭代周期。 基于高精度地图渲染、高精度定位算法、AR等技术的车道级导航、AR导航等产品快速上车,但同时随着人机交互多模发展以及3D沉浸式用户体验需求趋势下…...
Windows10资源管理器使用
文章目录 前言二、关联菜单操作1.分组展示2.添加选择复选框3.使用窗格模式4.功能区折叠二、“文件夹选项”对话框操作1.访问模式调整2.状态栏控制总结前言 目前Windows系统中的使用较多当属Windows10,资源管理器属于Windows系统中一个常用工具。本文总结了Windows 10 专业版下…...

【视频教程解读】Window上安装和使用autogluon V0.7
1.使用conda安装的python环境 教程使用的是极简版miniconda,由于我们的电脑中安装了anaconda,所以不需要进行进一步安装。python版本为3.9,博客里面有anaconda和python版本的对应关系。注意查看版本autogluon V0.4需要3.8或者3.9和3.10,pip版…...

10、Java继承与多态 - 内部类的概念与分类 1
10、Java继承与多态 - 内部类的概念与分类 1 什么是内部类? 如果一个事物的内部包含另一个事物,那么这就是一个内部包含另一个类,称作内部类; 例如:身体和心脏的关系,又如 -> 汽车和发动机的关系&#x…...

Java SE 面试题
文章目录 Java SE 面试题基本知识请简要介绍 Java SE。请解释 Java 的垃圾回收机制。请解释 Java 中的访问修饰符。 面向对象请解释封装、继承和多态。请解释接口和抽象类的区别。 集合框架请解释 ArrayList 和 LinkedList 的区别。请解释 Set 和 Map 接口。 异常处理请解释 Ja…...
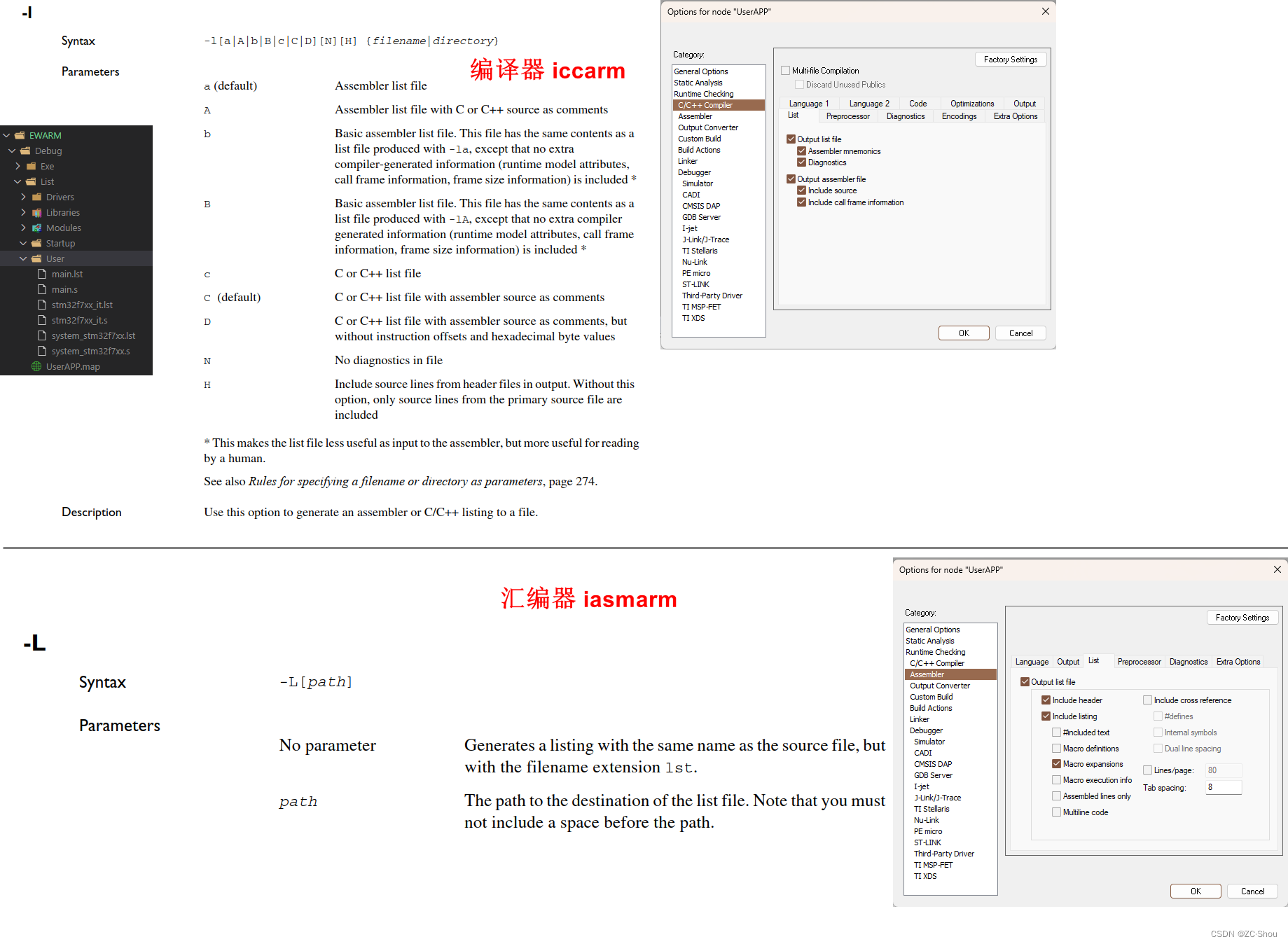
Linux 之十九 编译工具链、.MAP 文件、.LST 文件
.map 文件和 .lst 文件是嵌入式开发中最有用的俩调试辅助文件。现在主要从事 RISC-V 架构,开始与 GCC 打交道,今天就重点学习一下 GCC 的 .map 文件、.lst 文件,并辅助以 ARMCC 和 IAR 作为对比。 编译工具链 .map 文件和 .lst 文件都是由编…...

小 C 的数学(math)
祝大家劳动节快乐!!小手动起来 言归正传┏ (゜ω゜)☞ 题目描述 小 C 想要成为一名 OIer,于是他提前学习数学,为 OI 做好铺垫。这一天,他的数学老师给了一道题:给定正整数 a,以及给定一个区间 …...
应用运行环境实时洞察,亚马逊云科技Cisco AppDynamics展优势
Cisco AppDynamics(APM)产品,现已正式上线亚马逊云科技Marketplace(中国区域)。可以通过亚马逊云科技Marketplace(中国区域)网站,灵活便捷地部署该解决方案,以便充分利用云原生APM(应用性能管理…...
C++程序设计——lambda表达式
一、问题引入 在C98中,如果想对一个数据集合中的元素进行排序,可以使用sort()方法,但如果待排序元素为自定义类型,就需要用户自己定义排序时的比较规则。 随着C语法的发展,人们开始觉得其编写比较复杂,每次…...

Unity 高级程序员应该具备怎样的能力?要怎样成长为 Unity 高级程序员?
如何从零基础小白成长为 Unity 高级程序员?【全篇学习内容免费!快来白嫖】 高能预警,下文包含从零基础新手到高级程序员一站式技术学习、学习方法、心态等内容,供各个阶段的同学进行参考。 从零基础到高级程序员 上干货 话不多说…...

禁止触摸屏触控板手指缩放,需要这样处理
要禁止触摸屏的手指缩放,可以使用如下的CSS 只要在页面上使用css样式touch-action: none,就能禁止web在手机或平板上的缩放了。 <html style"touch-action: none;">注意: 使用 touch-action: none作用于html元素上࿰…...
opencv cuda版本windows编译
目录 1. 编译准备2. 编译3. 遇到的问题及解决方案3.1 boostdesc_bgm.i,vgg_generated_48.i等文件的缺失3.2 fatal error: features2d/test/test_detectors_regression.impl.hpp: 没有那个文件或目录 1. 编译准备 编译工具是cmakevisual studio2022,首先安装这两个工…...

python哲学
进入python编辑器模式下,输入import this 会打印python之禅(The Zen of Python) Beautiful is better than ugly. 优美胜于丑陋。 Explicit is better than implicit. 明了胜于晦涩。 Simple is better than complex. 简单胜过复杂。 Complex is better than co…...
用AIGC写iOS项目单元总结)
(2023)用AIGC写iOS项目单元总结
尝试开发的项目 项目功能 用 ChatGPT 开发了一个视频播放器。需要它编写的功能包括: ☆ 本地文件,在线 URL 播放,暂停 ☆ 点击空白区域弹出操作菜单,再点击消失 ☆ 手动横竖屏切换 ☆ 播放速度调整,限定 0.5, 1.0, …...

k8s扩容node节点会影响上面已存在的pod吗?
理论上不影响 扩容 Kubernetes 集群中的节点不会影响已经运行的 Pod,因为 Pod 是在节点上运行的,而不是在集群中运行的。当您添加新的节点时,Kubernetes 调度器会在新节点上启动新的 Pod,而已经运行的 Pod 会继续在它们当前的节点…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
