【贪婪技术】
目录
- 知识框架
- No.1 贪婪技术
- 一、问题引入
- 二、基本思想
- 三、问题实例:连续背包问题
- No.2 最小生成树问题
- 一、基本思想
- 二、Prim算法
- 1、主要思想和步骤
- 2、算法效率
- 三、Kruskal算法
- 1、主要思想和步骤
- No.3 Dijkstra算法
- 一、主要思想
- 二、问题实例:
- No.4 哈夫曼问题
- 一、哈夫曼树
知识框架
No.1 贪婪技术
一、问题引入
题目:找零问题
题意:用指定面额为d1>d2>…>dm的最少数量的硬币找出金额为n的零钱;
(就是说从给定的面额的硬币 使用 最少数量的硬币 凑出 金额 n)
d1=5角,d2=2角,d3=1角 ,d4=5分,d5=2分,d6=1分
当n=0.48的时候,请确定一种最佳选择序列的逻辑策略?
( 贪心的思想也就是 直接从最大的往下减;)
二、基本思想
贪婪法:通过一系列步骤来构造问题的解,每一步对目前构造的部分解做一个扩展,直到获得问题的完整解为止。
- 可行的:必须满足问题的约束
- 局部最优:是当前步骤中所有可行选择中最佳的局部选择
- 不可取消:选择一旦做出,在算法的后面步骤中就无法改变
在每一步中,它要求“贪婪”地选择最佳操作,并希望通过一系列局部的最优选择,能够产生一个整个问题(全局)的最优解
贪婪技术是否有效?
- 的确存在某类问题:一系列局部最优选择对于它们的每一个实例都能够产生一个最优解
- 或者我们关心的是近似解,或者只能满足于近似解
三、问题实例:连续背包问题
问题描述:
已知有n种物品和一个可容纳W重量的背包,每种物品I的重量为wi,假定将物品I的某一部分xi放入背包就会得到pi*xi的效益(0≤xi≤1, pi>0) ,采用怎样的装包方法才会使装入背包物品的总效益为最大呢?
下面的方案体现从不同角度进行的贪心,在局部最优解的情况下;有时候可能得到全局最优解的;
- 方案1:按物品价值降序装包;(贪心思想)
- 方案2:按物品重量升序装包;(贪心思想)
- 方案3:按物品价值与重量比值的降序装包;(贪心思想)
No.2 最小生成树问题
一、基本思想
给定n个点,把它们按照一种成本最低的方式连接起来,使得每一对点之间都有一条路径。这个问题可以表示成最小生成树问题。
(就是说有n个点,然后让你连接 n-1 条边使得这些点与点之间互通到达;使得连通成本最低)
- 连通图的一棵生成树是包含图的所有顶点的连通无环子图(也就是一棵树)
- 加权连通图的一棵最小生成树是图的权重最小的生成树
- 最小生成树问题:就是求给定的加权连通图的最小生成树问题
用穷举法来解决不现实;
- 随着图的规模增长,生成树的数量呈指数增加
- 生成一个给定图的所有生成树并非易事
二、Prim算法
1、主要思想和步骤
主要思想:Prim算法通过一系列不断扩张的子树来构造一棵最小生成树。
方法步骤:
- 从图的顶点集合V中任选一个单顶点,作为序列中的初始子树。
- 每一次迭代时,以一种贪婪的方式来扩张当前的生成树,即简单地把不在树中的最近顶点添加到树中(以一条权重最小的边和树中的顶点相连,树的形状是无所谓的)
- 当图的所有顶点都包含在所构造的树中以后,算法停止:每次只对树扩展一个顶点
方法要求:
- 对于每个不在当前树中的顶点,必须知道它连接树中顶点的最短边的信息;
- 每一个顶点附加两个标记:树中最近顶点的名称、相应边的权重(这两个标记在代码中是遍历来找最近顶点的);
Prim算法是否能产生一个最优解?
答案是肯定的
2、算法效率
Prim算法的实际运用算法效率 还是主要靠你使用的数据结构决定的;
- 表示图本身的数据结构
- 表示集合V-VT的优先队列的数据结构
如果图是由邻接链表表示的,并且优先队列是由最小堆实现的,那么该算法的运行时间属于O(|E|log|V|)
- 因为该算法进行了|V|-1次删除最小元素的操作,
- 并且进行了|E|次验证,每一种操作都是O(log|V|)
如果使用更先进的可能算法效率会更好!
三、Kruskal算法
1、主要思想和步骤
- Kruskal算法把一个加权连通图G=<V,E>的最小生成树看作是一个具有|V|-1条边的无环子图,并且边的权重和是最小的。
- 该算法通过对子图的一系列扩展来构造一棵最小生成树,这些子图总是无环的,但在算法的中间阶段,并不一定是连通的。
- 贪心到极致。
方法步骤:
- 首先,按照权重的非递减顺序对图中的边进行排序
- 然后,从一个空子图开始,扫描有序列表,试图把列表中的下一条边加到当前的子图中。(必须保证该添加不会导致一个回路)
- 必须要不成环才能加入;
算法详解:
- 对包含给定图的所有顶点和某些边的一系列森林所做的连续动作
- 初始森林是由|V|棵只有根结点的树构成的
- 最终的森林是由一棵树构成的,它就是该图的最小生成树
- 每次迭代的时候,从图的边的有序列表中取出下一条边(u,v),并找到包含顶点u和v的树,如果他们不是同一棵树,通过加入边(u,v)把这两棵树连成一棵更大的树
No.3 Dijkstra算法
一、主要思想
单起点最短路径问题:对于加权连通图的一个称为起点的给定顶点,求出它到所有其他顶点之间的一系列最短路径。
(也就是说给了一个起源点,就能够通过这个算法求得起源点到其它各个顶点的最短路径,是属于一步到位的)
方法步骤:
Dijkstra算法按照从给定起点到图中顶点的距离,顺序求出最短的路径。
- 首先,它求出从起点到最接近起点的顶点之间的最短路径
- 然后,求出第二近的,依此类推
二、问题实例:
主要针对的是边上权值非负情形的单源最短路径问题。
问题的提法:
给定一个带权有向图D与源点 v,求从 v 到D中其他顶点的最短路径。限定各边上的权值大于或等于0。
问题的解决步骤:(每次看的都是到源点v的距离比较)
为求得这些最短路径, Dijkstra提出按路径长度的递增次序, 逐步产生最短路径的算法。首先求出长度最短的一条最短路径,再参照它求出长度次短的一条最短路径,依次类推,直到从顶点v到其它各顶点的最短路径全部求出为止。
- 引入辅助数组dist。它的每一个分量dist[i]表示当前找到的从源点 v0到终点 vi 的最短路径的长度。初始状态:
- 若从源点v0到顶点 vi 有边, 则dist[i]为该边上的权值;
- 若从源点v0到顶点 vi 无边, 则dist[i]为∞。
- 假设 S 是已求得的最短路径的终点的集合,则可证明:下一条最短路径必然是从v0 出发,中间只经过 S 中的顶点便可到达的那些顶点vx (vx∈V-S )的路径中的一条。
- 每次求得一条最短路径后, 其终点vk 加入集合S,然后对所有的vi∈V-S,修改其 dist[i]值。
代码:
void dij(int index){//初始化vis,dis,以及main上面的变量;;memset(vis,0,sizeof(vis));memset(dis,inf,sizeof(dis));for(int i=0;i<n;i++)dis[i]=mp[index][i];dis[index]=0;way[index]=index;//初始化的人员,初始化的道路选择;;num[index]=people[index];cnt[index]=1;//找n个最短点,一个for找到一个点,vis【点】=1;//显然,第一个点是自己本身dis【index】=0;//第一部分:找最短的for(int i=0;i<n;i++){int u=-1,minn=inf;for(int j=0;j<n;j++){if(vis[j]==0&&dis[j]<minn){u=j;minn=dis[j];}}if(u==-1)break;vis[u]=1;//第二部分:更新距离for(int j=0;j<n;j++){if(vis[j]==0&&dis[j]>dis[u]+mp[u][j]){dis[j]=dis[u]+mp[u][j];num[j]=num[u]+people[j];way[j]=u;cnt[j]=cnt[u];//c出现下面这个条件啊,就会再出来一个最优判断。}else if(vis[j]==0&&dis[j]==dis[u]+mp[u][j]){cnt[j]=cnt[u]+cnt[j];if(num[j]<num[u]+people[j]){way[j]=u;num[j]=num[u]+people[j];}}}}
}
Dijkstra算法的步骤详细解释:
-
在第i次迭代开始以前,该算法已经确定了i-1条连接起点和离起点最近顶点之间的最短路径。他们构成了一棵子树Ti
- 和Ti的顶点相邻的顶点集合成为“边缘顶点”,以它们为候选对象,选出下一个最接近起点的顶点。
- 对于每一个边缘顶点u,该算法求出它到最近的树中顶点v的距离
- 给每个顶点附加两个标记
- 数字标记d指出目前为止该算法求出的从起点到该顶点间最短路径的长度
- 另一个指出在这条路径上倒数第二个顶点的名字。
-
在确定了加入树中的顶点u*以后,还需要做两个操作:
- 把u*从边缘集合中移到顶点集合
- 对于余下的每个边缘顶点u,如果通过权重为w(u*,u)的边和u相连,当du+w(u*,u)<du时,把u的标记分别更新为u和du+w(u*,u)
-
虽然从算法的标记和结构,Dijkstra算法和Prim算法的用法十分相似,且他们都会从余下顶点的优先队列中选择下一个顶点,但他们解决的是不同的问题。
No.4 哈夫曼问题
一、哈夫曼树
相关文章:

【贪婪技术】
目录 知识框架No.1 贪婪技术一、问题引入二、基本思想三、问题实例:连续背包问题 No.2 最小生成树问题一、基本思想二、Prim算法1、主要思想和步骤2、算法效率 三、Kruskal算法1、主要思想和步骤 No.3 Dijkstra算法一、主要思想二、问题实例: No.4 哈夫曼…...

谈「效」风生 | 如何找到现有研发体系的「内耗问题」?
#第3期:如何找到现有研发体系的「内耗问题」?# 在上一期《谈到提升效能,我们应该如何下手?》我们聊到开始做研发效能的四个要点:评估现有流程、引入自动化工具、建立度量指标、持续改进。本期就围绕「评估现有研发体系…...
Linux第四章
文章目录 前言一、快捷键小技巧二、软件安装三、systemctl控制软件启动关闭四、软链接五、日期和时区六、ip地址和主机名七、配置linux固定ip地址八、网络请求和下载九、端口十、进程管理十一、主机状态监控十二、环境变量十三、linux文件的上传和下载十四、压缩和解压总结 前言…...
HCIA-RS实验-路由配置-静态路由缺省路由
在计算机网络中,路由器是实现数据包转发的重要设备。它通过查找路由表中的路由信息,将数据包从源地址转发到目标地址。而静态路由和缺省路由则是路由表中的两种重要信息,下面我们来详细了解一下它们的概念、特点和应用。 目录 简述 一、静态…...

Unity API详解——Quaternion类
Quaternion类又称四元数,由x、y、z和w这4个分量组成,属于struct类型。在Unity中,用Quaternion来存储和表示对象的旋转角度。Quaternion的变换比较复杂,对于GameObject一般的旋转及移动,可以用Transform中的相关方法实现…...

8个免费的PNG素材网站推荐
很多设计小白都不知道什么是PNG。事实上,PNG是一种支持透明度的图像格式。当你想在设计中将图像与背景或文本混合时,它就会派上用场。 如果你没有时间为你正在处理的设计创建透明的PNG图像,你也可以使用我收集的PNG素材网站,以便…...

ChatGPT技术原理 第二章:自然语言处理基础
目录 2.1 语言模型 2.3 词嵌入 2.4 注意力机制 2.5 生成式模型 2.1 语言模型...
国民技术N32G430开发笔记(8)- 内部Flash的读写操作
N32G430 内部Flash的读写操作 1、主存储区最大为 64KB,也称作主闪存存储器,包含 32 个 Page,用于用户程序的存放和运行,以及数 据存储。 每一页的大小为2K字节 2、IAP 升级我们将64K的flash分区如下: Boot 0x800000…...

JVM 基本知识
目录 前言 一、JVM 内存区域划分 1.1 程序计数器 1.2 栈 1.3 堆 1.4 方法区 二、 JVM 类加载机制 2.1 类加载需要经过的几个步骤 2.1.1 Loading - 加载 2.1.2 Linking - 连接 2.1.3 initialization(初始化) 小结 经典面试题 三、JVM 垃圾…...

【源码解析】流控框架Sentinel源码解析
Sentinel简介 Sentinel是阿里开源的一款面向分布式、多语言异构化服务架构的流量治理组件。 主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 核心概念 资源 资源…...
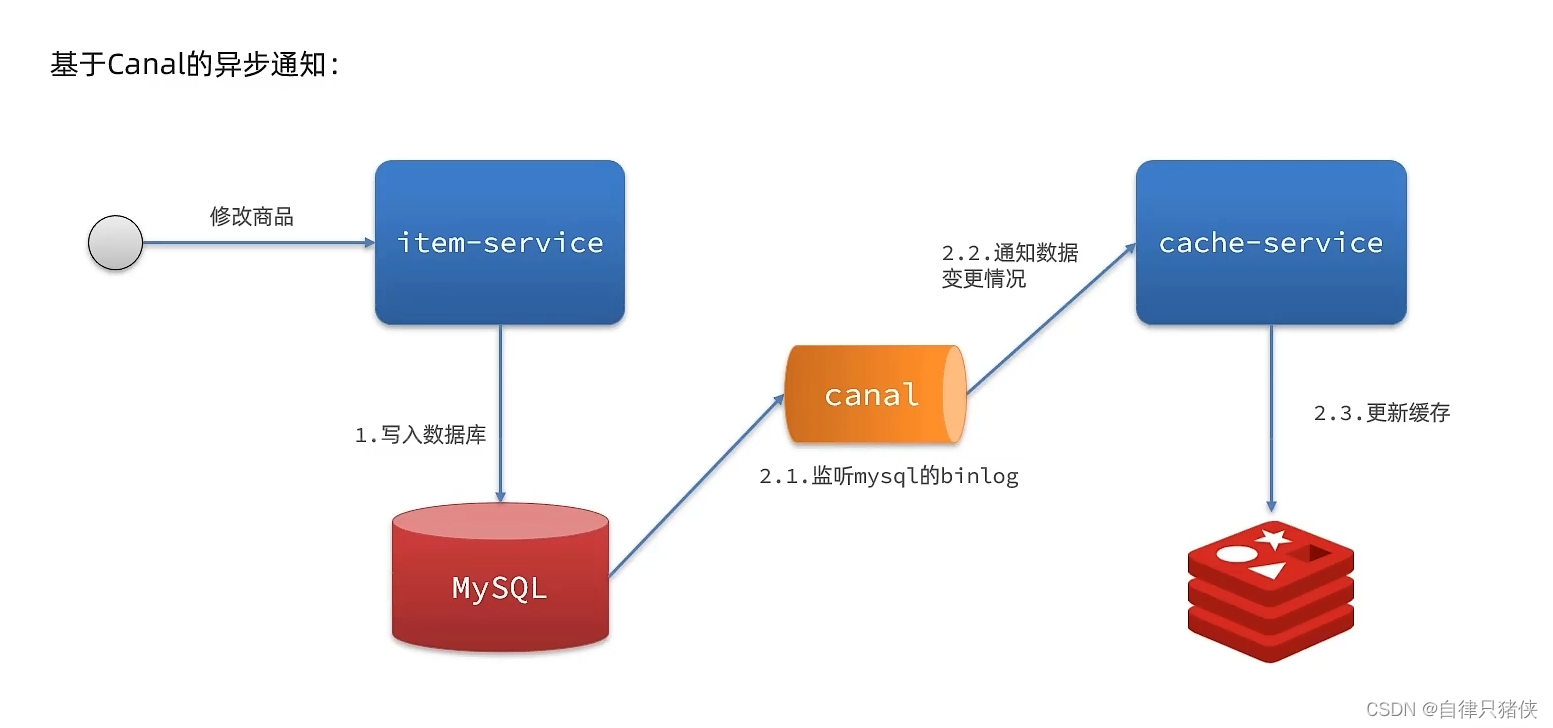
redis面试重点------源于黑马
缓存问题三兄弟 是因为不同的原因让请求全部打到了数据库而造成的问题 什么是缓存穿透? 缓存穿透是指查询一个数据,在redis和MySQL中都不存在。也就是查询一个数据不存在的数据,导致每次请求都会到达数据库,给数据造成很大的压力…...

jQuery知识点二
一、 jQuery 属性操作 1. 元素固有属性值 prop() 获取属性:prop("属性") 设置属性:prop("属性","属性值") 所谓元素固有属性就是元素本身自带的属性,比如 <a> 元素里…...

4 月份 火火火火 的开源项目
盘点 4 月份 GitHub 上 Star 攀升最多的开源项目,整个 4 月份最火项目 90% 都是 AI 项目(准确的说,最近半年的热榜都是 AI 项目) 本期推荐开源项目目录: 1. AI 生成逼真语音 2. 复旦大模型 MOSS! 3. 让画中…...

PAT A1011 World Cup Betting
1011 World Cup Betting 分数 20 作者 CHEN, Yue 单位 浙江大学 With the 2010 FIFA World Cup running, football fans the world over were becoming increasingly excited as the best players from the best teams doing battles for the World Cup trophy in South Af…...
Android 拍照以及相册中选择(适配高版本)————上传头像并裁剪(一)
前言 在项目研发中,相信大家都遇到过给用户增加头像照片的需求。 随着手机版本的不断更新,android 8、android 9、android 10、android 12、android 13、鸿蒙系统等等;遇到这个功能需求,大家肯定会想,“这还不好写&…...

带你了解现在的LED显示屏技术
随着LED显示屏技术的空前繁荣,LED显示屏产品备受关注,广泛应用于商业广告、实况播映、交通诱导、舞台演绎等领域,发展至今。你了解十大中国LED显示屏制造商吗? LED显示屏技术已经得到了长足的发展,现在的LED显示屏技术…...
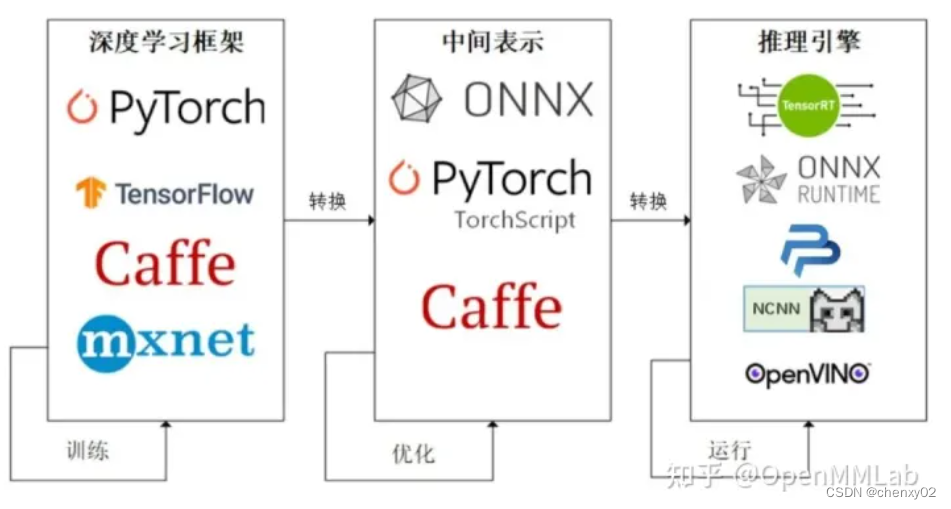
AI模型推理(1)——入门篇
前言 本文主要介绍AI模型推理的相关基础概念,为后续云原生模型推理服务的学习做准备。 初识模型部署 对于深度学习模型来说,模型部署指让训练好的模型在特定环境中运行的过程。相比于常规的软件部署,模型部署会面临更多的难题: …...

MySQL--表的基本查询--0410--15
目录 1. Create 1.1 insert 1.1.2 插入否则更新 1.2 replace 2.Retrieve 2.1 select 2.1.1 全列查询 2.1.2 指定列查询 2.1.3 查询字段为表达式 2.1.4 为查询结果指定名称 2.1.5 去重 2.2 where 2.2.1 > and > and < and < and 2.2.2 in between…...
Scala语言入门以及基本语法
文章目录 前言1.环境搭建1) IDEA中插件下载2) SDK下载配置 2.基本使用1)var与val的区别2) .基本数据类型3).字符串的基本用法4) 控制结构1) if else2) for 循环3) while循环 5)类6) 函数 前言 scala在一种简洁的高级语言中结合了面向对象和函数式编程。Scala的静态…...

Linux shell编程 循环语句for continue break
for循环是编程语言中一种循环语句 示例1:循环读取user.txt中的用户名,创建用户。设置密码。 for i in $(cat /opt/user.txt) douseradd $iecho 123456 | passwd --stdin $i done 示例2:循环读取ipaddr文本文件中地址,执行ping命令…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...
