两道链表经典算法题---链表有无环(基础+进阶)
生活就像一盒巧克力,你永远不知道你会得到什么。——《阿甘正传》

目前自己粗略的学完数据结构,正在开始刷算法题目。个人觉得算法是一个积累,循序渐进的的过程,需要不断加量,进而达到所谓的质。
链表作为数据结构一个重要的分支。我们没有理由不学好它,并且没有理由不刷一些链表的算法题。所以,今天想和大家讲解一下链表有无存在环的经典题目,并且由这道题目本身知识点发散开来,进而来解决一道有无环的进阶题目。看完这一篇文章,你的收获一定会非常之大。看完理解其中的原理之后,你只想说:秒,牛,我靠还能这样,·······,甚至你会直接关注我,给我点个赞。
目录:
一.判断链表是否有环
1.双指针作用(铺垫)
2.结论:环形链表的环一定在末尾,末尾没有NULL
3.具体步骤思路
4.详细代码
二.链表中环的入口节点
1.思路
2.两个结论:
4.详细代码
一.判断链表是否有环
先把题目给到大家,大家可以浏览一下:
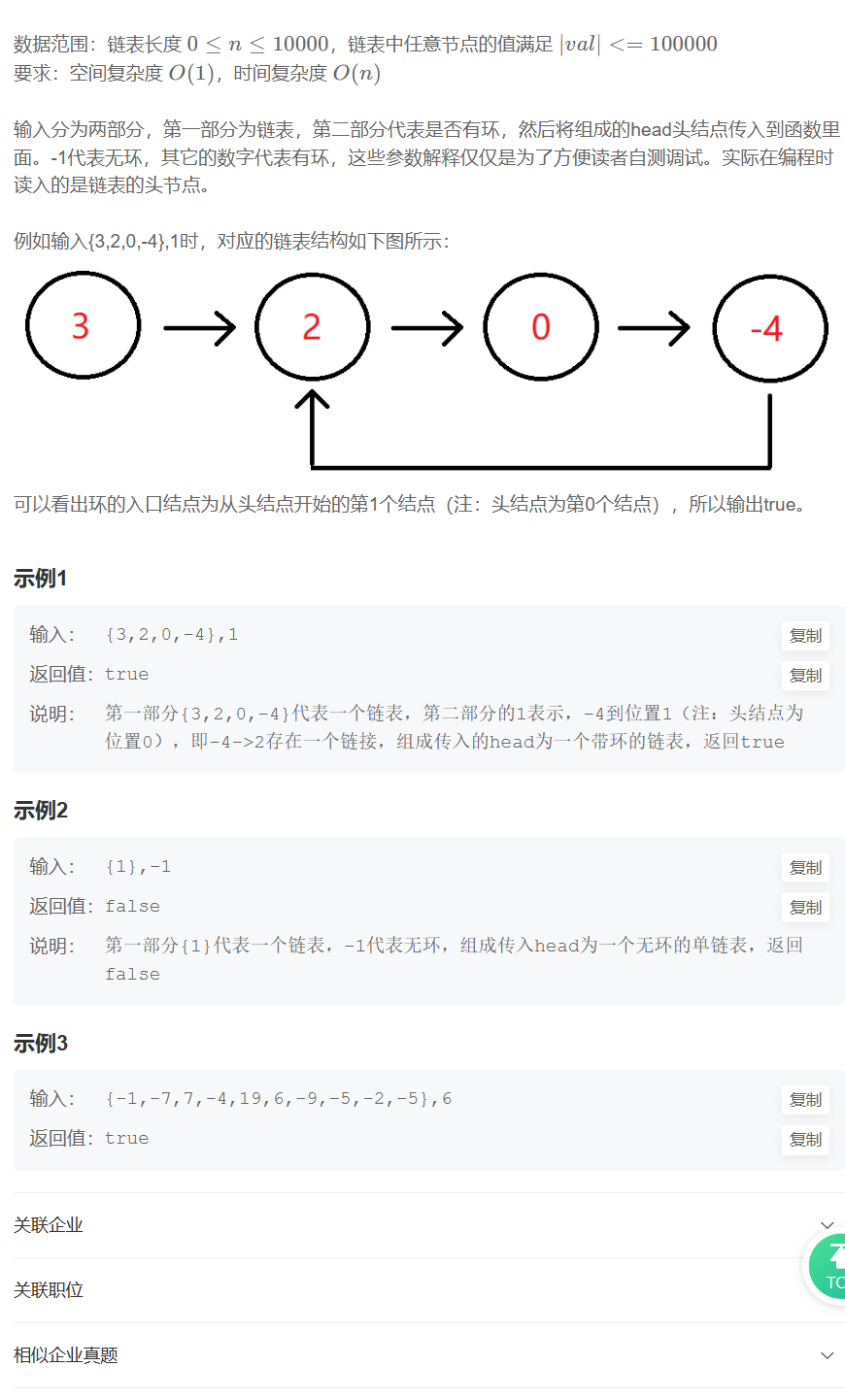
1.双指针作用(铺垫)
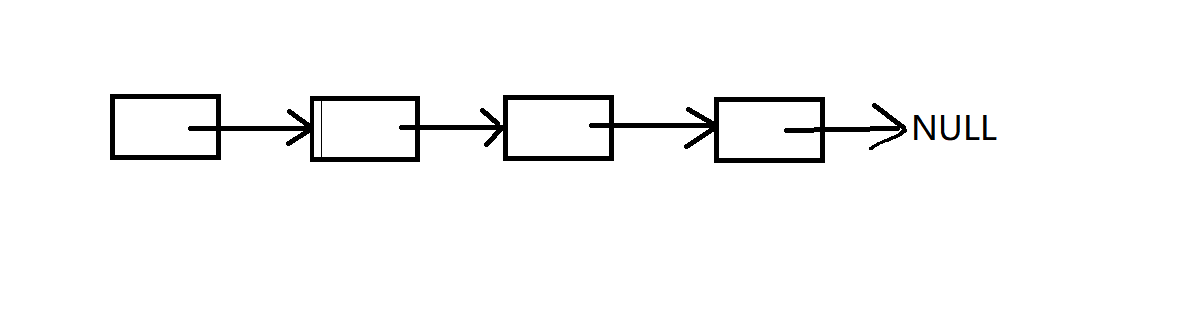
双指针的作用:由于单向链表(如上图)的每一个指针只能从头往后扫描,并不能从后往前的这一个局限性。所以,我们在解决单向链表的题目上,引入双指针。双指针指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个指针(特殊情况甚至可以多个),两个指针或是同方向访问两个链表,或是同方向访问一个链表(快慢指针)、或是相反方向扫描(对撞指针),从而建立一种手段,让这种手段为我们的目的服务。
2.结论:环形链表的环一定在末尾,末尾没有NULL
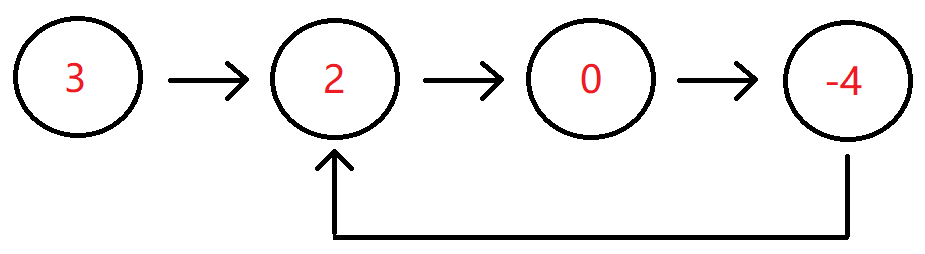
证明:看上图,在环2,0,-4中,没有任何一个节点可以指出环,它们只能在环内不断循环,链表不像二叉树,每个节点只有一个val值和一个next指针,也就是说一个节点只能有一个指针指向下一个节点,不能有两个指针。因此环后面不可能还有一条尾巴。如果是普通链表末尾一定有NULL(第一个图),那我们可以根据链表中是否有NULL判断是不是有环。
3.具体步骤思路
step 1:设置快慢两个指针,初始都指向链表头。
step 2:遍历链表,快指针每次走两步,慢指针每次走一步。
step 3:如果快指针到了链表末尾,说明没有环,因为它每次走两步,所以要验证连续两步是否为NULL。
step 4:如果链表有环,那快慢双指针会在环内循环,因为快指针每次走两步,因此快指针会在环内追到慢指针,二者相遇就代表有环。
·对于step4的进一步解释(个人理解):我们可以这样想,这个快指针一次是走两步,然后慢指针一次走一步,两指针距离会拉大,每循环一次两个指针的距离就会+1,我们假设在遇到环的那一刻他们之间的距离就是n,这时候慢指针在后面,快指针在这个环做周期性走动,慢指针就一步一步的跟上这个快指针,也就是这个n以减1的速度一直在靠近0,直到n=0,这个时候快慢指针就相遇。就能够判断链表有环。
画图解释,看下图:
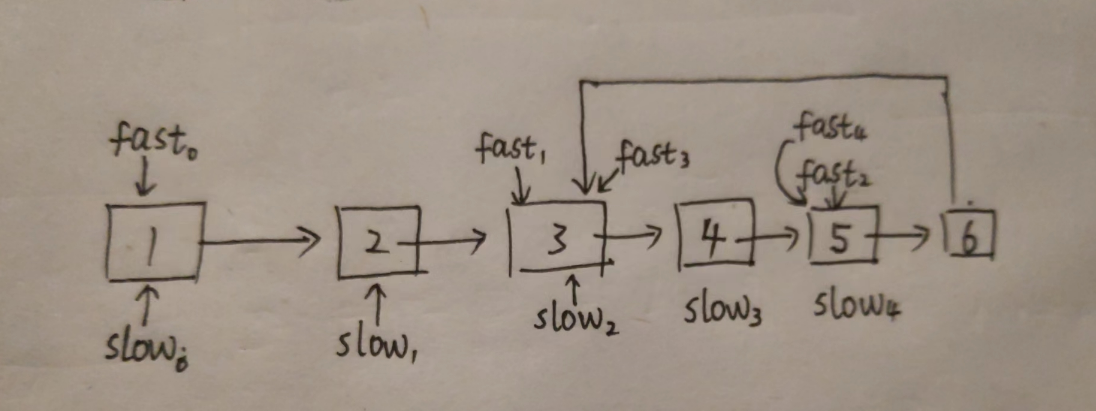
快指针走两步,慢指针走一步,最后相遇。一步一步分析。
4.详细代码
前面都是理论,接下来用代码实现:
#include <stdbool.h>struct ListNode {int val;struct ListNode *next;};//定义一个结点
bool hasCycle(struct ListNode* head )/返回类型是bool
{struct ListNode*fast=head;struct ListNode*slow=head;while(fast!=NULL&&fast->next!=NULL){fast=fast->next->next;//快指针走两步slow=slow->next;//慢指针走一步if(slow==fast)//如果相遇,则有环{return true;}}return false;
}二.链表中环的入口节点
在上一道题目的基础上,我们再来搞定这一道进阶题目:

1.思路
设置快慢指针,都从链表头出发,快指针每次走两步,慢指针一次走一步,假如有环,一定相遇于环中某点(结论一)。接着让两个指针分别从相遇点和链表头出发,两者都改为每次走一步,最终相遇于环入口(结论二)。以下是两个结论证明:
2.两个结论:
结论一:设置快慢指针,假如有环,他们最后一定相遇。
证明:设置快慢指针fast和slow,fast每次走两步,slow每次走一步。假如有环,两者一定会相遇(因为slow一旦进环,可看作fast在后面追赶slow的过程,每次两者都接近一步,最后一定能追上)。也即第一道题的结论。
结论二:两个指针分别从链表头和相遇点继续出发,每次走一步,最后一定相遇与环入口。
证明:设:
链表头到环入口长度为--a
环入口到相遇点长度为--b
相遇点到环入口长度为--c
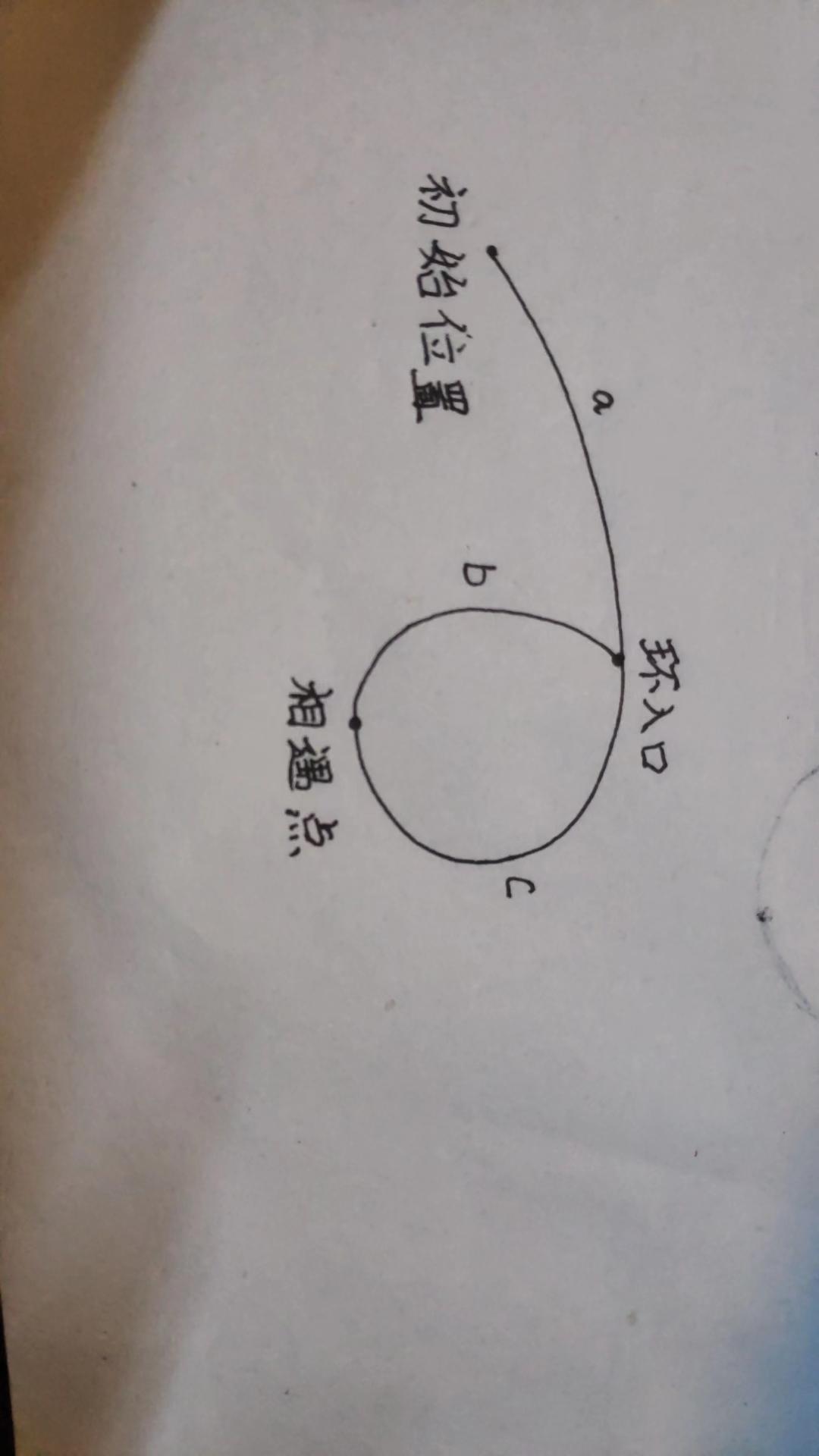
则:相遇时
快指针路程=a+(b+c)k+b ,k>=1 其中b+c为环的长度,k为绕环的圈数(k>=1,即最少一圈,不能是0圈,不然和慢指针走的一样长,矛盾)。
慢指针路程=a+b
快指针走的路程是慢指针的两倍,所以:
(a+b)*2=a+(b+c)k+b
化简可得:
a=(k-1)(b+c)+c 这个式子的意思是: 链表头到环入口的距离=相遇点到环入口的距离+(k-1)圈环长度。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发,最后一定相遇于环入口。
4.详细代码
前面都是理论,接下来用代码(C++)实现:
class Solution {
public:ListNode* EntryNodeOfLoop(ListNode* pHead) {ListNode*fast=pHead;ListNode*slow=pHead;while(fast!=nullptr&&fast->next!=nullptr){fast=fast->next->next;slow=slow->next;if(fast==slow)break;}if(!fast||!fast->next)return nullptr;slow=pHead;while(slow!=fast){fast=fast->next;slow=slow->next;}return slow;}
};以上是两道很经典的题目,就讲解到这里。
哦,对了,刚刚在构思这篇文章的过程中突然想到今天是情人节,然后然后,脑子里突然想起,正在看这篇文章的你可能你还没对象,所以呢哈哈哈,下一篇文章要讲解关于C++中new这类知识点,最后new一个自己想要的理想对象致敬在座的每个人。关记得关注我,下一篇今晚就发。

相关文章:

两道链表经典算法题---链表有无环(基础+进阶)
生活就像一盒巧克力,你永远不知道你会得到什么。——《阿甘正传》目前自己粗略的学完数据结构,正在开始刷算法题目。个人觉得算法是一个积累,循序渐进的的过程,需要不断加量,进而达到所谓的质。链表作为数据结构一个重…...

2023/1/14总结
今天学习的是c语法知识。 容器arry: 通俗来说这个容器就i是c语言的数组,和C中vevtor不同,arry是定长度的,而vector是动态数组。头文件为:<arry> 初始化: arry<数据类型,你所要声明…...

Python 之 NumPy 统计函数、数据类型和文件操作
文章目录一、统计函数1. 求平均值 mean()2. 中位数 np.median3. 标准差 ndarray.std4. 方差 ndarray.var()5. 最大值 ndarray.max()6. 最小值 ndarray.min()7. 求和 ndarray.sum()8. 加权平均值 numpy.average()二、数据类型1. 数据存储2. 定义结构化数据3. 结构化数据操作三、…...
互联网新时代要到来了(一)什么是Web3.0?
什么是Web3.0? tips:内容来自百度百科、知乎、搜狐新闻、李留白公众号、CSDN「Meta.Qing」博客等网页 什么是Web3.0?1.什么是Web3.0(概念介绍)?2.Web3.0简单理解3.Web3.0的技术特点4.Web3.0项目1.什么是Web3.0(概念…...

[Yocto] 直接向deploy/images目录部署binary
最近用yocto的时候碰到一个问题,有一些IP的FW binary是从别的地方直接拿来的,没有source code,有一个需求就是需要把它用wks script的方式把它们打包到最后的image里,这篇文章就是来谈谈这个问题。 yocto patch/deploy等做了什么 首先,虽然我们的code,bbfile,或者说pa…...
设备控制开发与实现(二))
HarmonyOS Connect原子化服务功能开发(Wi-Fi/Combo)设备控制开发与实现(二)
规设备控制 在“device”目录下的“DeviceApplication.java”文件中,在onInitialize函数中初始化应用。示例代码如下: Override public void onInitialize() {AiLifeServiceHelper.initApplication(this);DeviceHandlerAbility.register(this, "&qu…...

浅析 Makefile
Makefile逻辑 Makefile就是将一系列的工作流串在一起自动执行,构成Makefile最基本的要素是目标、依赖、命令。也就是为了实现目标需要哪些依赖并执行什么样的命令。 target: dependences1 dependences2 ... command1 command2 ...其中,target表示要生…...

保护品牌线上声誉的5种方法
我们如今生活在一个搜索便捷的世界,对于一个企业和个人来说,品牌的线上声誉也尤为重要。在客户考虑与您的公司开展业务之前,他们理所当然会先使用众多软件和平台搜索相关信息,以帮助他们了解和做决定。 因此,您的品牌…...

Java多重选择结构,超详细整理,适合新手入门
目录 一、什么是多重选择结构? 二、if 语句的语法 1、什么是嵌套if语句? 2、if 语句循环基本用法: 3、案例: 二、if...else多重选择结构语法 1、什么是if-else语句? 2、if...else 循环基本用法 3、案例&#…...

SCI写作,一定要避开这些“雷点”!
SCI论文写作中,除了要符合各部分的写作要求,还有许多细节问题需要我们注意,不然可能一不小心就会“踩雷”。 今天我们就来和大家分享SCI各个部分写作时的注意事项。 下面就进入正题! SCI写作注意事项 01 标题的拟定 1.避免使用无…...
))
3GPP-NR Band14标准定义频点和信道(3GPP V17.7.0 (2022-12))
Reference test frequencies for NR operating band n14 Table 4.3.1.1.1.14-1: Test frequencies for NRoperating band n14 and SCS 15 kHz CBW [MHz]carrierBandwidth...
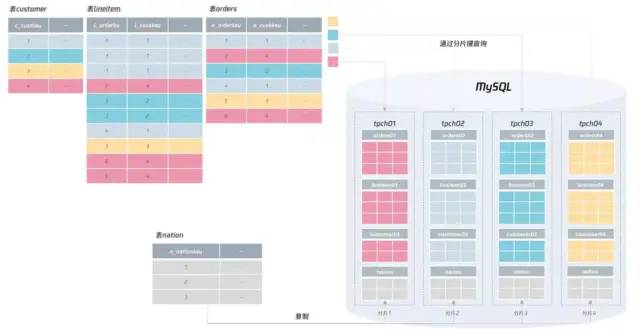
分库分表索引设计:分布式环境下的 主键索引、二级索引、全局索引的最佳设计实践
文章目录主键选择索引设计全局表唯一索引总结结语主键选择 对主键来说,要保证在所有分片中都唯一,它本质上就是一个全局唯一的索引。如果用大部分同学喜欢的自增作为主键,就会发现存在很大的问题。 因为自增并不能在插入前就获得值…...

2023年全国最新保安员精选真题及答案
百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、单选题(1-480题)以下备选答案中只有一项最符合题目要求&a…...

计算机网络之http07 http2,http3
HTTP1.2 http1.2都做了哪些优化 (1)头部压缩 使用HPACK压缩头部 头部冗长,大量重复字段 (2)二进制帧 将报文头部和内容字符编码改为二进制格式 字符编码未压缩 (3)并发传输 解决h1.1 队头阻塞问题,多车道 …...
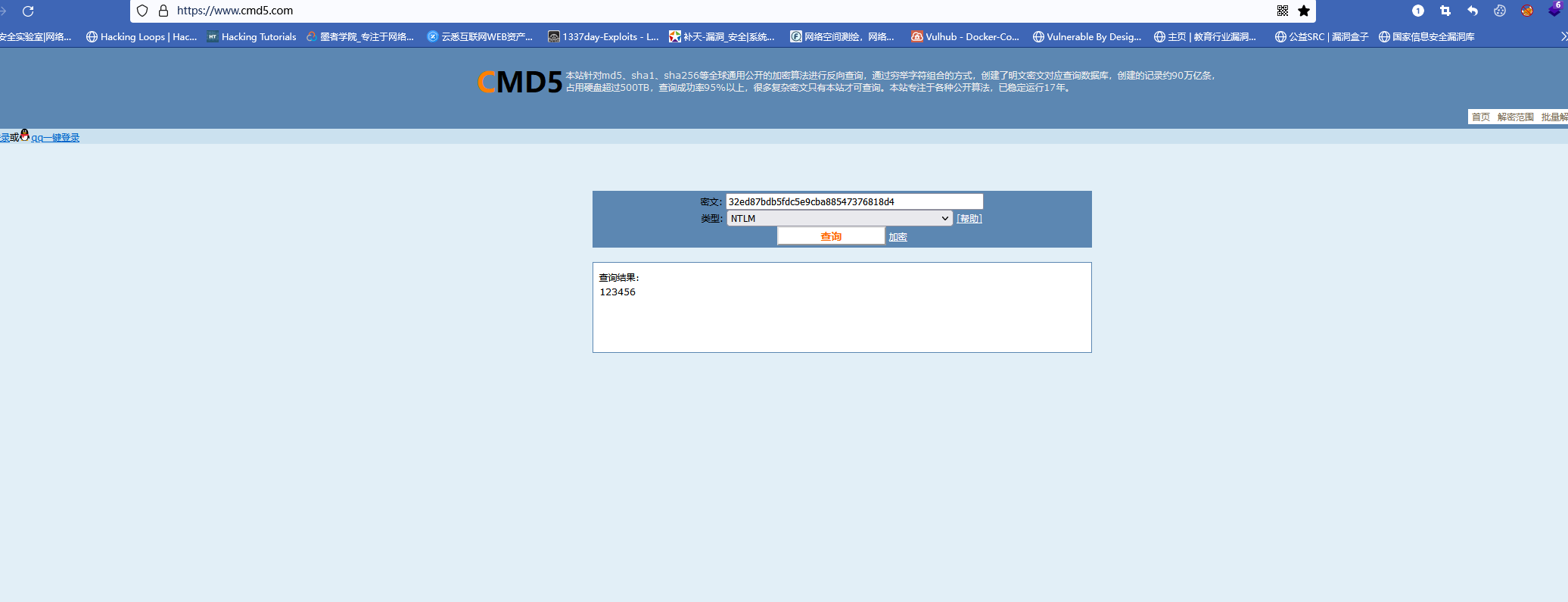
内网渗透(二十五)之Windows协议认证和密码抓取-使用Hashcat和在线工具破解NTLM Hash
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...
TongWeb8防止System.exit代码导致的进程停止
现象:当应用中存在System.exit 、Runtime.exit代码执行时,会导致TongWeb进程停止,从而产生如下日志:2023-02-14 09:47:36 [WARN] - The web application [webtest01] is still processing a request that has yet to finish. This…...
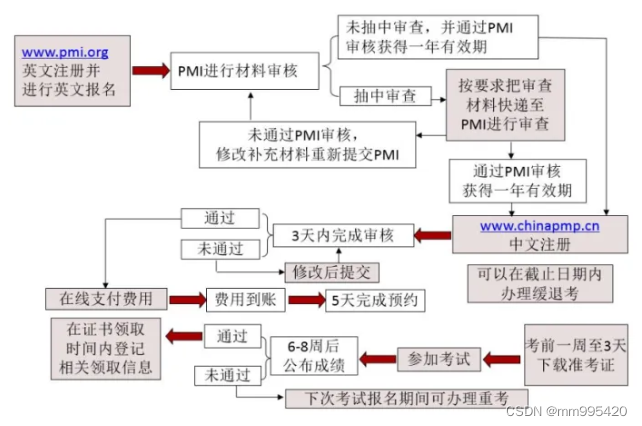
PMP每年考几次,费用如何?
一,PMP每年考几次,怎么准备? PMP项目管理证书是美国PMI发起的在全球200多个国家进行的项目管理专业人士资格认证,它的含金量和给认证者带来的作用已经很明显。 PMP考试是项目管理专业人士资格认证考试,通过PMP考试是…...
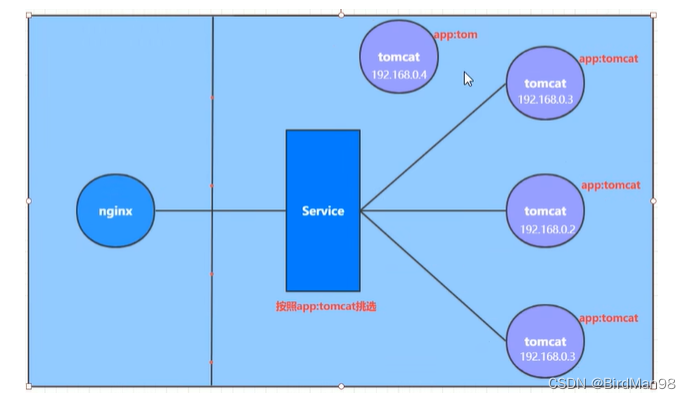
【Kubernetes】【一】Kubernetes介绍
Kubernetes介绍 应用部署方式演变 在部署应用程序的方式上,主要经历了三个时代: 传统部署:互联网早期,会直接将应用程序部署在物理机上 优点:简单,不需要其它技术的参与 缺点:不能为应用程序定…...

C语言:结构体
往期文章 C语言:初识C语言C语言:分支语句和循环语句C语言:函数C语言:数组C语言:操作符详解C语言:指针详解 目录往期文章前言1. 结构体的声明2. 结构体变量的定义和初始化3. 结构体成员的访问3. 结构体传参…...

搭建pclpy环境与读取pandaset数据并转换为pkl格式为pcd格式
1.搭建pclpy环境 问题:需要处理pcd文件,于是开始摸索搭建环境,有python-pcl,但是安装过程频频出现问题,于是转向pclpy。 参考链接:GitHub - davidcaron/pclpy: Python bindings for the Point Cloud Libr…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
