Python超矩形
文章目录
- 距离函数
- 矩形分割
Rectangle是
scipy.spatial中封装的类,其构造函数只需输入最小值和最大值的数组即可,并且可通过内置的
volume方法计算广义的体积。
from scipy.spatial import Rectanglerec = Rectangle((0,0), (5,5))
print(rec.maxes) # [5. 5.]
print(rec.mins) # [0. 0.]
print(rec.volume()) # 25
rec3 = Rectangle((0,0,0), (5,5,5))
print(rec3.volume()) # 125
距离函数
通过min_distance_point/max_distance_point可以计算某点到矩形内部的最近/最远距离
print(rec.min_distance_point((3,3)))
# 0.0
print(rec.max_distance_point((3,3)))
# 4.242640687119285
由于(3,3)在矩形内部,所以最小距离为0;而最大距离则位于(0,0)处。
通过min_distance_rectangle/max_distance_rectangle方法可以计算一个矩形和另一个矩形之间的最小/最大距离
rec2 = Rectangle((5,5),(10,10))
rec.max_distance_rectangle(rec2, 2)
# 14.142135623730951
rec.min_distance_rectangle(rec2, 2)
# 0.0
由于两个矩形存在交点,所以最近距离为0,而最远距离则在(0,0), (10,10)之间。
这4个距离函数均采用闵可夫斯基距离的定义,默认阶数为2,通过第二个参数p,可以修改距离的定义。对于点 x , y x,y x,y而言,具体的距离公式为
d p = ∑ i ∣ x i − y i ∣ p p d_p = \sqrt[p]{\sum_i \vert x_i-y_i\vert^p} dp=pi∑∣xi−yi∣p
>>> rec.max_distance_point((3,3),1)
6.0
当p=1时,表示曼哈顿距离,即 ∑ i ∣ x i − y i ∣ \sum_i |x_i-y_i| ∑i∣xi−yi∣,对于 ( 0 , 0 ) (0,0) (0,0)到 ( 3 , 3 ) (3,3) (3,3)来说就是 3 + 3 = 6 3+3=6 3+3=6。
矩形分割
通过split,可以对矩形进行分割,其输入参数有2,分别是分割所在坐标轴,以及该坐标轴处的刻度,效果如下
rec.split(0, 2)
(<Rectangle [(0.0, 2.0), (0.0, 5.0)]>, <Rectangle [(2.0, 5.0), (0.0, 5.0)]>)
由于Rectangle定义的超矩形可以有不同的维度,换言之,一维的矩形就是线段,三维的矩形就是立方体。一旦接受了这种设定,那么矩形分割就可以理解为线段分割,或者立方体分割。有了这个,就可以更加便捷地进行非线性寻优了。
在scipy.optimize中,提供了DIRECT算法,运用的就是这种思想。
而在点云处理中使用更加频繁的八叉树,则是矩形分割更加直观的案例,open3d中实现了这种算法,以二维超矩形为例,则其运算流程可理解为四叉树。
仍以六个数据点作为研究对象:{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)},如果以 [ 0 , 10 ) [0,10) [0,10)为坐标空间,那么通过对这个空间四等分,可得到下左图
 | =》 |  |
令所有的分割都是左闭右开的,那么被分割后的四个区间中,除了右下角的方块包含三个点之外,剩下三个方块都只有一个点。只有一个点的方块显然就没法继续分割了,而第四个方块则可继续分割,得到右图。
这样,右下角的方块被继续分成了四个小方块,且每个小方块的元素都不超过一个,所以无法继续再分,四叉树也就完成了。
相关文章:

Python超矩形
文章目录 距离函数矩形分割 Rectangle是 scipy.spatial中封装的类,其构造函数只需输入最小值和最大值的数组即可,并且可通过内置的 volume方法计算广义的体积。 from scipy.spatial import Rectanglerec Rectangle((0,0), (5,5)) print(rec.maxes) …...
【软考数据库】第五章 计算机网络
目录 5.1 网络功能和分类 5.2 OSI七层模型 5.3 TCP/IP协议 5.4 传输介质 5.5 通信方式和交换方式 5.6 IP地址 5.7 IPv6 5.8 网络规划和设计 5.9 其他考点补充 5.10 网络安全技术 5.11 网络安全协议 前言: 笔记来自《文老师软考数据库》教材精讲ÿ…...

深眸科技|深度学习、3D视觉融入机器视觉系统,实现生产数智化
随着“中国制造2025”战略加速落实,制造业生产线正在加紧向智能化、自动化和数字化转型之路迈进。而人工智能技术的兴起以及边缘算力持续提升的同时,机器视觉及其相关技术也在飞速发展,并不断渗透进工业领域,拓展应用场景的同时&a…...

DateFormat使用时需要注意:多线程下需要特殊处理
前言 工作或学习过程中难免会接触到时间(Date)相关的内容,比如String类型转为Date类型,或者Date类型转为String类型,jdk为我们提供了一套完善的日期格式化工具,DateFormat类,使用者可以使用该接…...
Packet Tracer - 研究直连路由
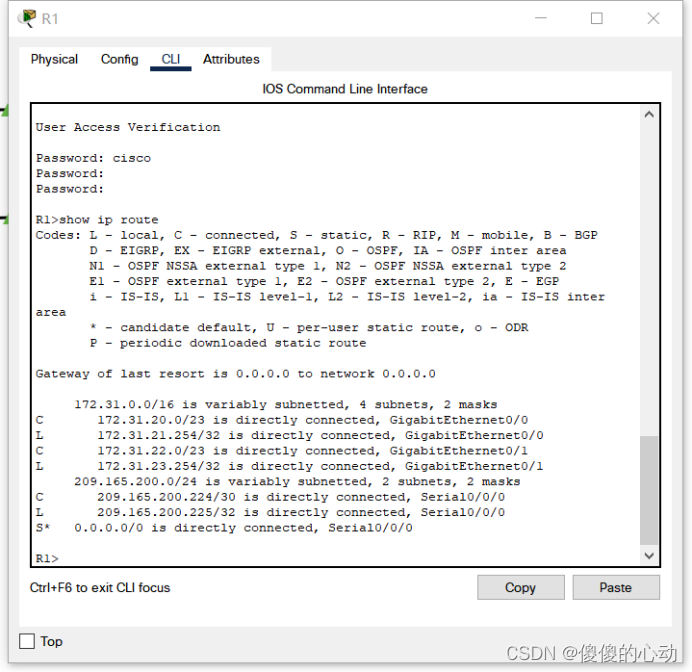
Packet Tracer - 研究直连路由 目标 第 1 部分:研究 IPv4 直连路由 第 2 部分:研究 IPv6 直连路由 拓扑图 背景信息 本活动中的网络已配置。 您将登录路由器并使用 show 命令发现并回答以下有关直连路由的问题。 注:用户 EXEC 密码是 c…...

大专生程序员找工作的一点小建议 知识分享 经验分享
最近呢有人在私信我 就问我说我呢是一个大专生 大专毕业 学历呢也不是很好 我但是我学的是这个计算机 这样一个专业 然后呢现在找工作找不到 就这样的一个要求 让我们呢给一些建议 当然就是私底下在网上聊吗 就会给 也相信 我的一个建议是什么样的 就是你首先你要去找工作的 首…...

PyCaret:低代码自动化的机器学习工具
PyCaret简介 随着ChatGPT和AI画图的大火,机器学习作为实现人工智能的底层技术被大众越来越多的认知,基于机器学习的产品也越来越多。传统的机器学习实现方法需要较强的编程能力和数据科学基础,这使得想零基础尝试机器学习变得非常困难。 机器…...
【Hello Network】网络编程套接字(三)
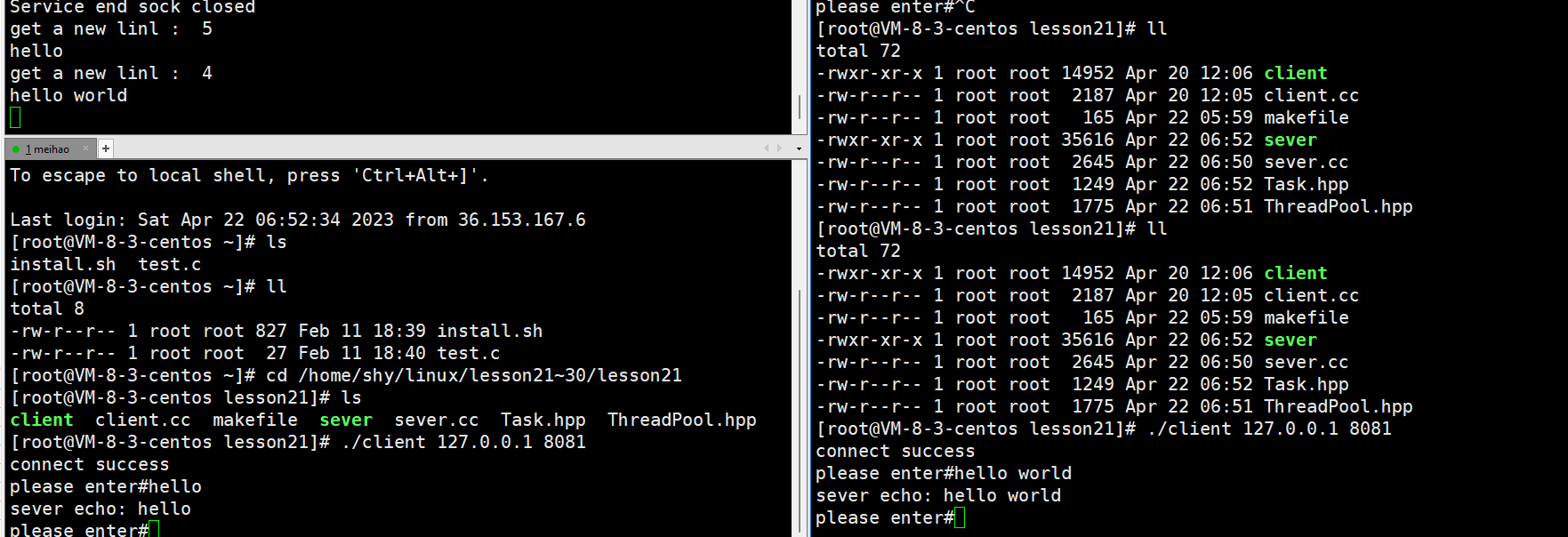
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:简单介绍下各种类型的Tcp协议 各种类型Tcp服务器 多进程版的TCP网络程序捕捉SIGCHLD信号让孙子进程执行任务 多线程TCP网络程序线程池版多线程TCP网络…...

3.4 只读存储器
学习目标: 学习只读存储器(ROM)的目标可以包括以下内容: 了解ROM的基本概念、分类以及适用场景。掌握ROM的电路原理、逻辑结构和读取方式。熟悉ROM的编程方式和编程工具。理解ROM与EPROM、EEPROM和闪存的区别和联系。了解ROM在计…...

从后端开发转大数据开发怎么样?
很多做后端的小伙伴,在某一个瞬间,都想转行大数据,那这种想法可行嘛? 转大数据的最初原因很简单,就是好几个同事都转了,他们的收入瞬间提高了好多,于是在同事的内推我也就跟着转了,…...
编程式导航路由跳转到当前路由(参数不变),多次执行会抛出NavigatorDuplicated的禁告错误?
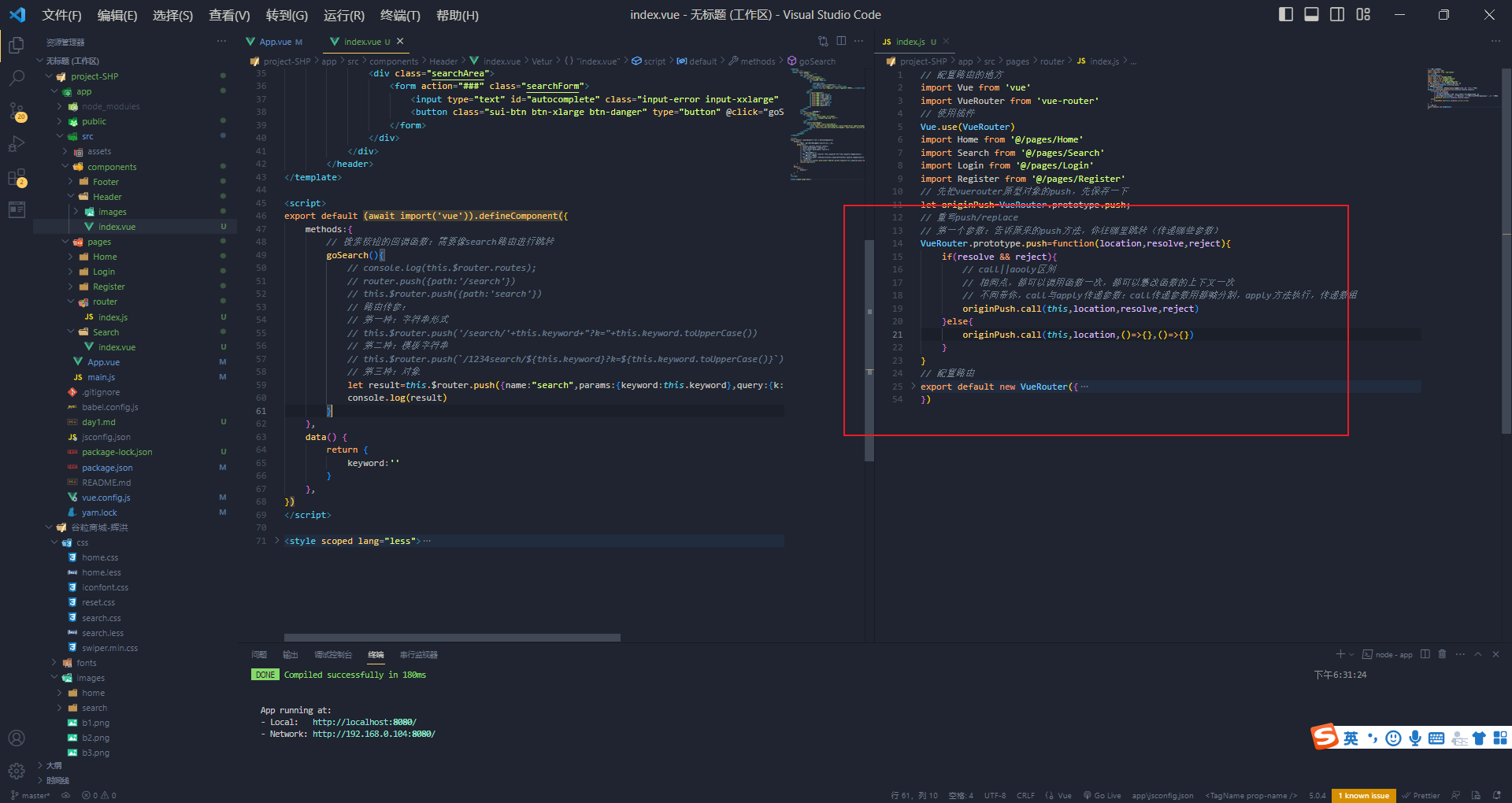
重写push与replace方法 编程式导航路由跳转到当前路由(参数不变),多次执行会抛出NavigatorDuplicated的禁告错误? 路由跳转有俩种形式:声明式导航,编程式导航 声明式导航没有这类问题的,因为…...

AppArmor无内核及系统日志的问题及解决
在AppArmor中,正常情况下,一旦违反了规则,是能够在内核及系统日志中看到相关信息的。比如:在Ubuntu下正常产生的日志信息(示例)如下: kernel: [140321.028000] audit(1191433716.584:1578): t…...

本地更改配置ssh密钥和更改github网址
配置 SSH 密钥以进行身份验证,可以遵循以下步骤: 生成SSH密钥 打开 Git Bash 终端 在 Windows 上,可以打开 Git Bash 终端。通常,可以在开始菜单中搜索 Git Bash 并启动它。一旦打开了 Git Bash 终端,将进入一个基于…...

MATLAB函数封装2:QT调用封装函数
在利用MATLAB进行封装函数之后,最主要的目的是对函数进行调用,能够对矩阵运算和其他算法的运行进行快捷处理。 在有了MATLAB函数之后封装成DLL文件之后,在QT中添加动态链接库,就可以实现函数的调用过程,这个过程相对简…...
AJAX和JSON
1、什么是AJAX? AJAX(ASynchronous JavaScript And XML)异步的JavaScript 和 XML; 由Jesse James Garrett 在他的文章AJAX:A New Approoch to Web Applications中首次提出。 ajax(Web数据交互方式)_百…...

源码:SharedPreferences分析
一、持久化方式: DataStore:稳定性 MMKV:效率 SharedPreferneces 区别: 功能MMKVJetpack DataStoreSharedPreferneces是否阻塞主线程否否是是否线程安全是 是 是是否支持跨进程是否否是否类型…...

大二一个学期学这么点内容,没有概念,只有实操
如何查看所有的数据库: Show databases; 如何进入某个数据库: use xxx; 如何新进数据库: Create database jx; 如何删除数据库: Drop database jx; 如何查看所有的表格: Show tables; 如何创建数据表…...
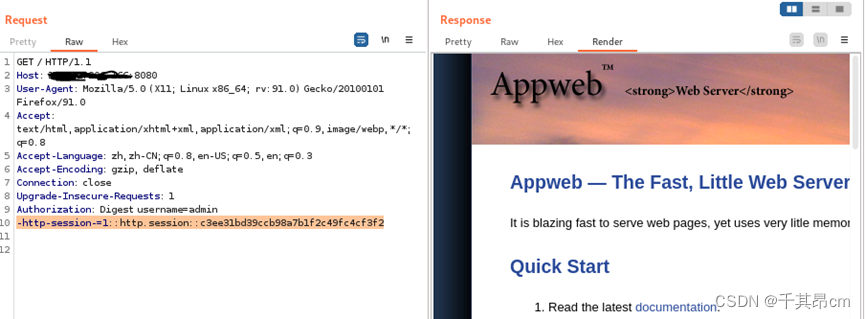
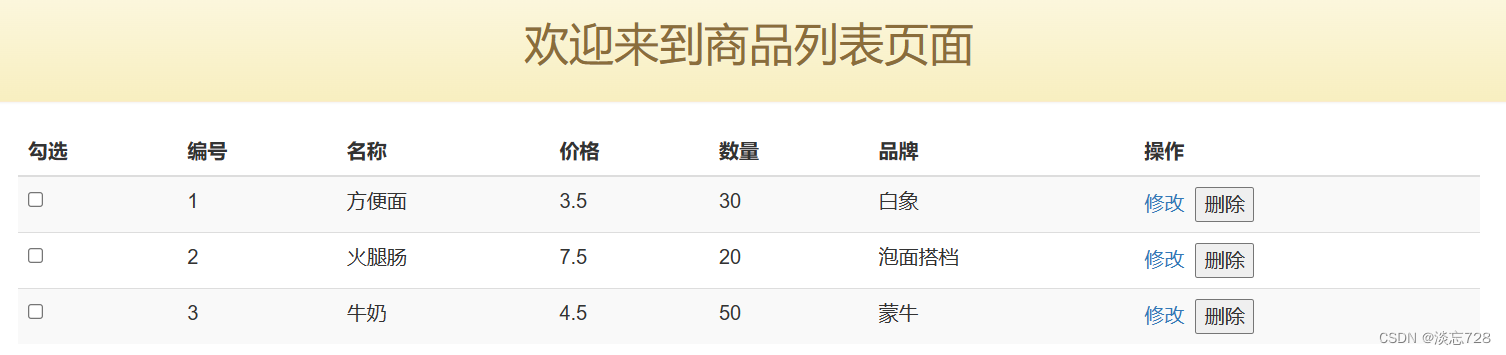
AppWeb 身份验证绕过漏洞 (CVE-2018-8715)
当前漏洞环境部署在vulhub,当前验证环境为vulhub靶场(所有实验均为虚拟环境) 实验环境:攻击机----kali 靶机:centos7 1、进入靶场,启动环境 2、访问AppWeb控制台:http://your-ip:8080 使用用户名、密码adm…...

为什么监控摄像头画面不如手机拍摄视频画面清晰
一天和一个做餐饮的朋友吃饭聊天,他提出一个问题,几百块的监控摄像头就是纯粹做监控功能 ,视频拍摄的画面为什么还没有几百元的手机拍摄的视频画面清晰,对于此特意查了一下技术资料,整理一下,以备下次再详细…...

EU GMP附录一与关键区域空气微生物取样方案及相关法规标准解读
2022版EU GMP附录一与关键区域空气微生物取样方案疑问解答 3月30日2022版EU GMP附录一与关键区域空气微生物取样方案网络研讨会期间,我们收集到了部分参会听众针对该主题所提出的常见问题。根据以下这些问题,lighthouse微生物应用专家将来为您答疑解惑。…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...
