【机器学习分支】重要性采样(Importance sampling)学习笔记
重要性采样(importance sampling)是一种用于估计概率密度函数期望值的常用蒙特卡罗积分方法。其基本思想是利用一个已知的概率密度函数来生成样本,从而近似计算另一个概率密度函数的期望值。
想从复杂概率分布中采样的一个主要原因是能够使用式(11.1)计算期望。重要采样(importance sampling)的方法提供了直接近似期望的框架,但是它本身并没有提供从概率分布 p ( z ) p(z) p(z)中采样的方法,也就是我们无法从式(11.1)直接过渡到(11.2)
E [ f ] = ∫ f ( z ) p ( z ) d z (11.1) \mathbb{E}[f] = \int f(z)p(z)dz \tag{11.1} E[f]=∫f(z)p(z)dz(11.1) f ^ = 1 L ∑ l = 1 L f ( z ( l ) ) (11.2) \hat{f} = \frac{1}{L}\sum\limits_{l=1}^L f(z^{(l)}) \tag{11.2} f^=L1l=1∑Lf(z(l))(11.2)公式(11.2)给出的期望的有限和近似依赖于能够从概率分布 p ( z ) p(z) p(z)中采样。然而,假设直接从 p ( z ) p(z) p(z)中采样无法完成,但是对于任意给定的 z z z值,我们可以很容易地计算 p ( z ) p(z) p(z)。一种简单的计算期望的方法是将 z z z空间离散化为均匀的格点,将被积函数使用求和的方式计算,形式为
E [ f ] ≃ ∑ l = 1 L p ( z ( l ) ) f ( z ( l ) ) \mathbb{E}[f] \simeq \sum\limits_{l=1}^Lp(z^{(l)})f(z^{(l)}) E[f]≃l=1∑Lp(z(l))f(z(l))这种方法的一个明显的问题是求和式中的项的数量随着 z z z的维度指数增长。此外,正如我们已经注意到的那样,我们感兴趣的概率分布通常将它们的大部分质量限制在 z z z空间的一个很小的区域,因此均匀地采样非常低效,因为在高维的问题中,只有非常小的一部分样本会对求和式产生巨大的贡献。我们希望从 p ( z ) p(z) p(z)的值较大的区域中采样,或理想情况下,从 p ( z ) f ( z ) p(z)f(z) p(z)f(z)的值较大的区域中采样。
与拒绝采样的情形相同,重要采样基于的是对提议分布 q ( z ) q(z) q(z)的使用,我们很容易从提议分布中采样,如下图所示:

重要采样解决的是计算函数 f ( z ) f(z) f(z)关于分布 p ( z ) p(z) p(z)的期望的问题,其中,从 p ( z ) p(z) p(z)中直接采样比较困难。相反,样本 z ( l ) {z^{(l)}} z(l)从一个简单的概率分布 q ( z ) q(z) q(z)中抽取,求和式中的对应项的权值为 p ( z ( l ) ) / q ( z ( l ) ) p(z^{(l)})/q(z^{(l)}) p(z(l))/q(z(l)),这样就可以还原到从 p ( z ) p(z) p(z)中取样。
上述过程中的式子,我们可以通过 q ( z ) q(z) q(z)中的样本 { z ( l ) } \{z^{(l)}\} {z(l)}的有限和的形式来表示期望
E = ∫ f ( z ) p ( z ) d z = ∫ f ( z ) p ( z ) q ( z ) q ( z ) d z ≃ 1 L ∑ l = 1 L p ( z ( l ) ) q ( z ( l ) ) f ( z ( l ) ) \mathbb{E} = \int f(z)p(z)dz \ = \int f(z)\frac{p(z)}{q(z)}q(z)dz \ \simeq \frac{1}{L}\sum\limits_{l=1}^L\frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)}) E=∫f(z)p(z)dz =∫f(z)q(z)p(z)q(z)dz ≃L1l=1∑Lq(z(l))p(z(l))f(z(l))其中 r l = p ( z ( l ) ) / q ( z ( l ) ) r_l = p(z^{(l)}) / q(z^{(l)}) rl=p(z(l))/q(z(l))被称为重要性权重(importance weights),修正了由于从错误的概率分布 q ( z ) q(z) q(z)中采样引入的偏差。
对于上述过程,举个栗子:
我们的待计算函数为 h ( x ) = e − 2 ∣ x − 5 ∣ h(x)=e^{-2|x-5|} h(x)=e−2∣x−5∣,待采样分布为 p ( x ) = 1 10 , x ∼ u ( 0 , 10 ) p(x)=\dfrac{1}{10} ,x \sim\mathcal{u}(0,10) p(x)=101,x∼u(0,10),从 h ( x ) h(x) h(x)的图像中明显可以看出,在中间部分的 h ( x ) p ( x ) h(x)p(x) h(x)p(x)对期望贡献较大,而两边几乎可以忽略不计,所以此时使用均匀分布采样并不合理。

基于此,我们引入了新的采样分布函数 q ( x ) = 1 2 π e − ( x − 5 ) 2 2 q(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{(x-5)^2}{2}} q(x)=2π1e−2(x−5)2

这使得在 h ( x ) h(x) h(x)较大的位置取值更多,需要的采样点更少。
而更常见的情形是,概率分布 p p p的计算结果没有标准化,也就是 p ( z ) = p ~ ( z ) / Z p p(z) = \tilde{p}(z) / Z_p p(z)=p~(z)/Zp中我们只知道 p ~ ( z ) \tilde{p}(z) p~(z),其中 p ~ ( z ) \tilde{p}(z) p~(z)可以很容易地由 z z z计算出来(可能没有函数表达式),而 Z p Z_p Zp未知( p ~ ( z ) \tilde{p}(z) p~(z)无法积分算)。类似的,我们可能希望使用重要采样分布 q ( z ) = q ~ ( z ) / Z q q(z) = \tilde{q}(z) / Z_q q(z)=q~(z)/Zq中的 q ~ ( z ) \tilde{q}(z) q~(z),它具有相同的性质。于是我们得到:
E [ f ] = ∫ f ( z ) p ( z ) d z = Z q Z p ∫ f ( z ) p ~ ( z ) q ~ ( z ) q ( z ) d z ≃ Z q Z p 1 L ∑ l = 1 L r ~ l f ( z ( l ) ) \mathbb{E}[f] = \int f(z)p(z)dz \ = \frac{Z_q}{Z_p}\int f(z)\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \ \simeq \frac{Z_q}{Z_p}\frac{1}{L}\sum\limits_{l=1}^L\tilde{r}_lf(z^{(l)}) E[f]=∫f(z)p(z)dz =ZpZq∫f(z)q~(z)p~(z)q(z)dz ≃ZpZqL1l=1∑Lr~lf(z(l))
其中 r ~ l = p ~ ( z ( l ) ) / q ~ ( z ( l ) ) \tilde{r}_l = \tilde{p}(z^{(l)}) / \tilde{q}(z^{(l)}) r~l=p~(z(l))/q~(z(l))。
我们还可以使用同样的样本集合来计算比值 Z p / Z q Z_p / Z_q Zp/Zq,结果为:
Z p Z q = 1 Z q ∫ p ~ ( z ) d z = ∫ p ~ ( z ) q ~ ( z ) q ( z ) d z ≃ 1 L ∑ l = 1 L r ~ l \frac{Z_p}{Z_q} = \frac{1}{Z_q}\int\tilde{p}(z)dz = \int\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \ \simeq \frac{1}{L}\sum\limits_{l=1}^L\tilde{r}_l ZqZp=Zq1∫p~(z)dz=∫q~(z)p~(z)q(z)dz ≃L1l=1∑Lr~l
第一个等式中 Z p Z_p Zp用 ∫ p ~ ( z ) d z \int\tilde{p}(z)dz ∫p~(z)dz等价计算了出来,第二个等式中 Z q Z_q Zq用 q ( z ) = q ~ ( z ) / Z q q(z) = \tilde{q}(z) / Z_q q(z)=q~(z)/Zq替代
因此:
E [ f ] ≃ ∑ l = 1 L w l f ( z ( l ) ) \mathbb{E}[f] \simeq \sum\limits_{l=1}^Lw_lf(z^{(l)}) E[f]≃l=1∑Lwlf(z(l))其中: w l = r ~ l ∑ m r ~ m = p ~ ( z ( l ) ) / q ( z ( l ) ) ∑ m p ~ ( z ( l ) ) / q ( z ( l ) ) w_l = \frac{\tilde{r}_l}{\sum_m\tilde{r}_m} = \frac{\tilde{p}(z^{(l)})/q(z^{(l)})}{\sum_m\tilde{p}(z^{(l)})/q(z^{(l)})} wl=∑mr~mr~l=∑mp~(z(l))/q(z(l))p~(z(l))/q(z(l))
这也就是我们最终要找样本点计算的式子
最终,我们达到了“利用一个已知的概率密度函数 q ( z ) q(z) q(z)来生成样本,从而近似计算另一个概率密度函数的期望值 E [ f ] = ∫ f ( z ) p ( z ) d z \mathbb{E}[f] = \int f(z)p(z)dz E[f]=∫f(z)p(z)dz”这一目的。
参考:
- 【PRML】【模式识别和机器学习】【从零开始的公式推导】11.1.4重要性采样 11.1.5采样-重要性-重采样 11.1.6采样与EM算法
- Importance Sampling - VISUALLY EXPLAINED with EXAMPLES!
相关文章:

【机器学习分支】重要性采样(Importance sampling)学习笔记
重要性采样(importance sampling)是一种用于估计概率密度函数期望值的常用蒙特卡罗积分方法。其基本思想是利用一个已知的概率密度函数来生成样本,从而近似计算另一个概率密度函数的期望值。 想从复杂概率分布中采样的一个主要原因是能够使用…...

三角回文数+123
三角回文数:用户登录 问题描述 对于正整数 n, 如果存在正整数 k 使得 n123⋯kk(k1)/2, 则 n 称为三角数。例如, 66066 是一个三角数, 因为 66066123⋯363 。 如果一个整数从左到右读出所有数位上的数字, 与从右到左读出所有数位 上的数字是一样的, 则称这个数为…...

JAVA常用的异步处理方法总结
前言 在java项目开发过程中经常会遇到比较耗时的任务,通常是将这些任务做成异步操作,在java中实现异步操作有很多方法,本文主要总结一些常用的处理方法。为了简化,我们就拿一个实际的案例,再用每种方法去实现…...

GitLab统计代码量
gitlab官方文档:https://docs.gitlab.com/ee/api/index.html 1、生成密钥 登录gitlab,编辑个人资料,设置访问令牌 2、获取当前用户所有可见的项目 接口地址 GET请求 http://gitlab访问地址/api/v4/projects?private_tokenxxx 返回参数 …...

Linux TCP MIB统计汇总
概述 在 linux > 4.7 才将所有TCP丢包收敛到 函数 tcp_drop 中 指标详解 cat /proc/net/netstat 格式化命令 cat /proc/net/netstat | awk (f0) {name$1; i2; while ( i<NF) {n[i] $i; i }; f1; next} (f1){ i2; while ( i<NF){ printf "%s%s %d\n", …...

记录 docker linux部署jar
第一步 web sso user admin 中yml文件还原到阿里mysql数据库 第二步 各个jar进行打包处理 第三步 正式服务器的Jar备份 第四步 拉取以上jar包 到正式服务器中 第五步 查看 docker images 其中 web_service 1.0.2是上一个版本 上一个版本build 镜像命令是这样的(需…...

【Linux】教你用进程替换制作一个简单的Shell解释器
本章的代码可以访问这里获取。 由于程序代码是一体的,本章在分开讲解各部分的实现时,代码可能有些跳跃,建议在讲解各部分实现后看一下源代码方便理解程序。 制作一个简单的Shell解释器 一、观察Shell的运行状态二、简单的Shell解释器制作原理…...

onMeasure里如何重置只有1个子view一行满屏, 若有多个自适应一行
onMeasure里如何重置只有1个子view一行满屏, 若有多个自适应一行 可以尝试在 onMeasure 方法中重写 measureChildWithMargins 或 measureChild 方法来实现这个需求。 对于只有一个字的 View,我们可以把它的宽度设为屏幕宽度,高度设为最大高度,这样这个 View 就会占满一整行…...
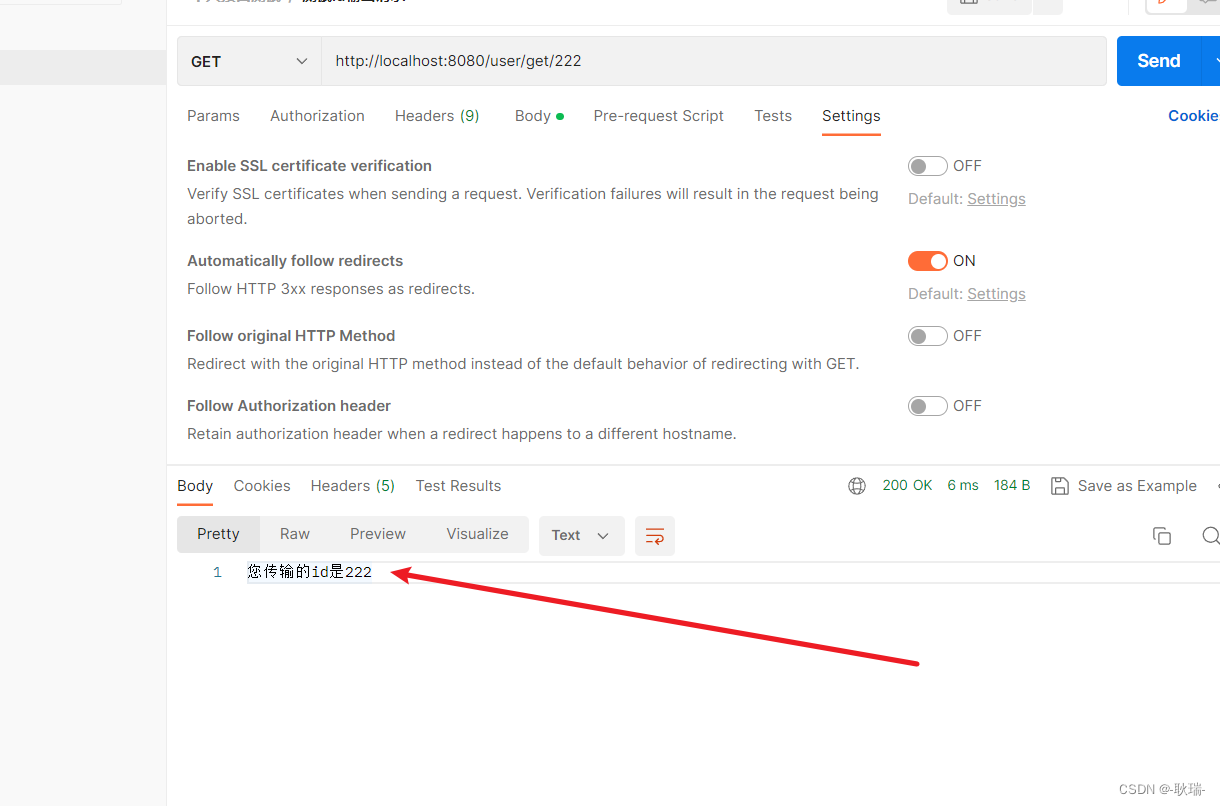
Postman创建项目 对接口发起请求处理
查看本文之前 您需要理解了解 Postman 的几个简单工作区 如果还没有掌握 可以先查看我的文章 简单认识 Postman界面操作 那么 掌握之后 我们就可以正式来开启我们的接口测试 我们先选择 Collections 我们点上面这个加号 多拉一个项目出来 然后 我们选我们刚加号点出来的项目…...

在Vue3项目中js-cookie库的使用
文章目录 前言1.安装js-cookie库2.引入、使用js-cookie库 前言 今天分享一下在Vue3项目中引入使用js-cookie。 1.安装js-cookie库 js-cookie官网 安装js-cookie,输入 npm i js-cookie安装完成可以在package.json中看到: 安装以后,就可…...

【论文笔记】Attention和Visual Transformer
Attention和Visual Transformer Attention和Transformer为什么需要AttentionAttention机制Multi-head AttentionSelf Multi-head Attention,SMA TransformerVisual Transformer,ViT Attention和Transformer Attention机制在相当早的时间就已经被提出了&…...

独立IP服务器和共享IP服务器有什么区别
在选择一个合适的服务器时,最常见的选择是共享IP服务器和独立IP服务器。尽管两者看起来很相似,但它们有着很大的不同。本文将详细介绍共享IP服务器和独立IP服务器的不同之处,以及如何选择适合您需求的服务器。 一、什么是共享IP服务器? 共享…...

Java8
Java8 (一)、双列集合(二)、Map集合常用api(三)、Map集合的遍历方式(四)、HashMap(五)、LinkedHashMap(六)、TreeMap(七&a…...

nn.conv1d的输入问题
Conv1d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue) in_channels(int) – 输入信号的通道。在文本分类中,即为词向量的维度out_channels(int) – 卷积产生的通道。有多少个out_channels,就需要多少个1维…...
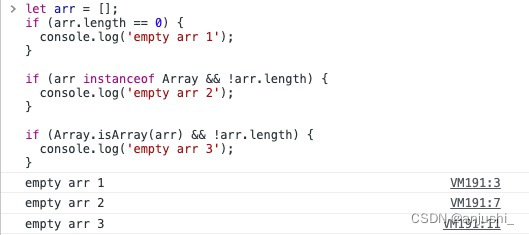
js判断是否为null,undefined,NaN,空串或者空对象
js判断是否为null,undefined,NaN,空串或者空对象 这里写目录标题 js判断是否为null,undefined,NaN,空串或者空对象特殊值nullundefinedNaN空字符串("")空对象(…...

Java每日一练(20230501)
目录 1. 路径交叉 🌟🌟 2. 环形链表 🌟🌟 3. 被围绕的区域 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏…...

从零开始学习Web自动化测试:如何使用Selenium和Python提高效率?
B站首推!2023最详细自动化测试合集,小白皆可掌握,让测试变得简单、快捷、可靠https://www.bilibili.com/video/BV1ua4y1V7Db 目录 引言: 一、了解Web自动化测试的基本概念 二、选择Web自动化测试工具 三、学习Web自动化测试的…...

fastdfs环境搭建
安装包下载路径 libfastcommon下载地址:https://github.com/happyfish100/libfastcommon/releasesFastDFS下载地址:https://github.com/happyfish100/fastdfs/releasesfastdfs-nginx-module下载地址:https://github.com/happyfish100/fastdf…...

有什么牌子台灯性价比高?性价比最高的护眼台灯
由心感叹现在的孩子真不容易,学习压力比我们小时候大太多,特别是数学,不再是简单的计算,而更多的是培养学生其他思维方式,有时候我都觉得一年级数学题是不是超纲了。我女儿现在基本上都是晚上9点30左右上床睡觉&#x…...

信息系统项目管理师 第9章 项目范围管理
1.管理基础 1.产品范围和项目范围 产品范围:某项产品、服务或成果所具有的特征和功能。根据产品需求来衡量。 项目范围:包括产品范围,是为交付具有规定特性与功能的产品、服务或成果而必须完成的工作。项目管理计划来衡量 2.管理新实践 更加注重与商业分析师一起…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
