排序算法总结
常见排序算法的时间复杂度、空间复杂度及稳定性分析:
| 时间复杂度 | 空间复杂度 | 是否有稳定性 | ||
| 基于比较的排序算法 | 选择排序 | O(N^2) | O(1) | 否 |
| 冒泡排序 | O(N^2) | O(1) | 是 | |
| 插入排序 | O(N^2) | O(1) | 是 | |
| 归并排序 | O(N*logN) | O(N),每次需要额外一个数组用于拷贝 | 是 | |
| 快排 | O(N*logN) | O(logN) | 否 | |
| 堆排序 | O(N*logN) | O(1),数组本身可以作为堆,用的只是有限几个变量 | 否,堆插入的过程不稳定如果最后插入一个 | |
| 不基于比较的排序算法 | 计数排序 | O(N) | O(M),M表示数的枚举值个数 | 是 |
| 基数排序 | O(N) | O(N) | 是 |
(1)不基于比较的排序,对样本数据有严格的要求,不易改写
(2)基于比较的排序,只要规定好两个样本怎么比大小就可以直接复用。
(3)基于比较的排序,时间复杂度的极限是O(N*logN)
(4)时间复杂度为O(N*logN),额外空间复杂度低于O(N)且稳定的基于比较的排序是不存在的。
(5)为了绝对速度选快排,为了省空间选堆排,为了稳定性选归并
稳定性分析:
选择排序:肯定做不到稳定性,比如原来的数组是[5,5,5,5,5,3,5,5],每次选最小的与0位置做交换,那原来0位置的5会越过1,2,3,4位置的5来到5位置。
冒泡排序:取决于相等的时候怎么处理相等,如果相等不交换就能保证稳定(如果相等还要交换的话也就不会有稳定性了)
插入排序:和冒泡排序一样,取决于怎么处理相等。
归并排序:也是处理相等的时候,相等的时候先拷贝左边的就可以保证稳定性(先拷贝右边不行,因为左组的元素在原来数组中是在右组的元素之前的)。
快速排序:无法保证稳定性,因为Partition过程做不到稳定,比如原数组是[4,4,4,4,1,4,3],我们以快排1.0为例,先选数组最后一个数字去做划分值,当遍历到4为止的1的时候,1比3小,需要和0位置的4做交换,0位置的4换到了4位置,跨过了1,2,3位置的4,其他快排也是类似的
堆排序:完全保证不了稳定性,整体调成大根堆或者小根堆的过程就不稳定,比如数组是[4,4,4,4,4,4,4,4,6],前7个4插入结束后,堆是这样的:

当最后一个6来了之后需要先跟3交换,然后和1交换,然后和0交换
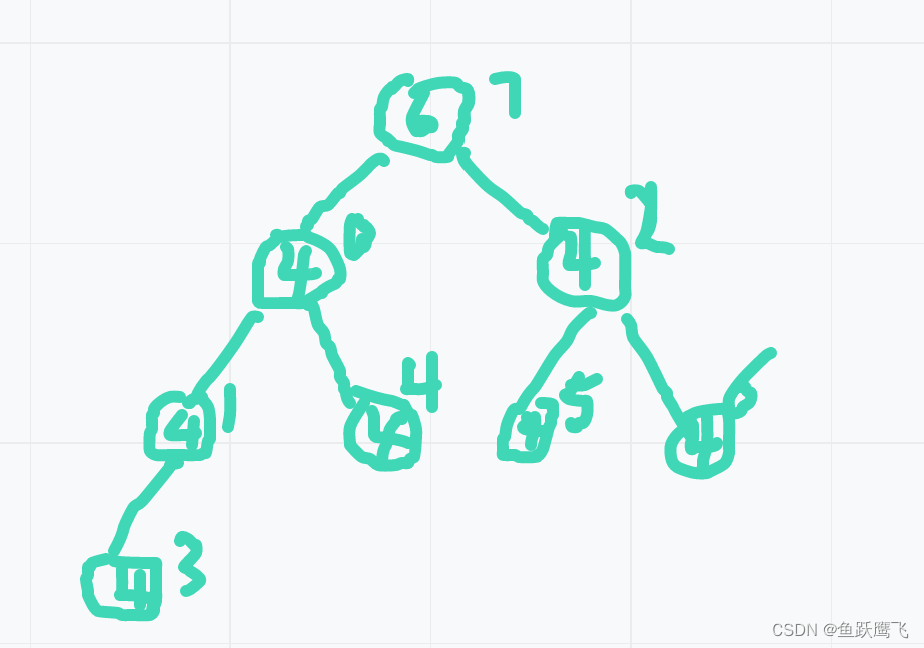
原数组中1位置的4跑到了2位置之后,3位置的4跑到了4,5,6之后
三种O(N * logN)的比较排序,如果追求速度用快排,因为
单纯追求速度使用快排:虽然时间复杂度是一样的,但是快排的常数时间更好
追求稳定性用归并:三个算法中唯一的稳定性算法
追求绝对的省空间适用堆排序:数组本身可以作为堆,用的只是有限几个变量
目前来说时间复杂度为O(N*logN),额外空间复杂度低于O(N)且稳定的基于比较的排序是不存在的。
Java自带的Arrays.sort的排序逻辑:
如果是基础类型,使用改进后的快排,因为基础类型排序,稳定性不重要而快排确实是最快的,时间常数最好的
如果是引用类型使用归并排序,也许稳定性不一定需要,但是未知的东西我们不能认为没有,只能考虑最差情况,为了保证稳定性,O(N*logN)只能用归并,且要保证相等时拷贝左边半区的元素
部分语言中会在快排的算法中写类似L + 60 < R使用插入排序的逻辑,这是因为虽然插入排序的时间复杂度是O(N^2),但是它的常数项更好,在数据量比较小的情况下插入排序执行时间可能小于快速排序,60是在长期实验条件下确定的值,这是工程上对于排序算法的改进。
相关文章:

排序算法总结
常见排序算法的时间复杂度、空间复杂度及稳定性分析: 时间复杂度空间复杂度是否有稳定性基于比较的排序算法选择排序 O(N^2)O(1)否 冒泡排序O(N^2)O(1)是插入排序O(N^2)O(1)是归并排序O(N*logN)O(N),每次需要额外一个数组用于拷贝是快排O(N*log…...
java+jsp企业物流货运快递管理系统servlet
功能需求具体描述: (1)用户功能模块包括用户登录注册,用户信息的修改,用户发布货物信息,给客服人员留言,对运输公司进行评价。 (2)企业功能模块包括企业注册登录,企业信息的修改,受理用户发布的…...

【ROS仿真实战】获取机器人在gazebo位置真值的三种方法(三)
文章目录 前言一. 使用ROS tf库二、 使用Gazebo Model Plugin三、 使用libgazebo_ros_p3d插件四、总结 前言 在ROS和Gazebo中,获取机器人的位置信息通常通过ROS消息传递进行。在这篇文章中,我们将介绍三种获取机器人在Gazebo中位置真值的方法࿱…...
——FontDialog(史上最全))
Winform从入门到精通(35)——FontDialog(史上最全)
文章目录 前言一、属性1、Name2、AllowScriptChange3、AllowSimulations4、AllowVectorFonts5、AllowVerticalFonts6、Color7、FixedPitchOnly8、Font9、FontMustExist10、MaxSize11、MinSize12、 ScriptsOnly13、ShowApply14、ShowColor15、ShowEffects16、ShowHelp...

AcWing 854. Floyd求最短路Floyd模板
Floyd算法: 标准弗洛伊德算法,三重循环,基于动态规划。 循环结束之后 d[i][j]存储的就是点 i 到点 j 的最短距离。 需要注意循环顺序不能变:第一层枚举中间点,第二层和第三层枚举起点和终点。 特点: 1.复杂…...
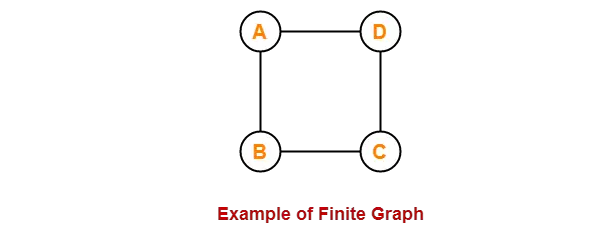
Graph Theory(图论)
一、图的定义 图是通过一组边相互连接的顶点的集合。 In this graph, V { A , B , C , D , E } E { AB , AC , BD , CD , DE } 二、图的类型 2.1 Finite Graph A graph consisting of finite number of vertices and edges is called as a finite graph. Null Graph Tri…...

[Python]生成 txt 文件
前段时间有位客户问: 你们的程序能不能给我们生成个 txt 文件,把新增的员工都放进来,字段也不需要太多,就要 员工姓名/卡号/员工编号/员工职位/公司 这些字段就行了,然后我们的程序会去读取这个 txt 文件,拿里面的内容,读完之后会这个文件删掉 我: 可以接受延迟吗?可能没办法实…...

GeoTools实战指南: 自定义矢量样式并生成截图
GeoTools实战指南: 自定义矢量样式并生成截图 介绍 本段代码的主要功能是将矢量数据(Shapefile)渲染成一张图片。 准备环境 首先,您需要将GeoTools库添加到您的项目中。使用Maven或Gradle添加依赖项,或者直接下载GeoTools的jar文件并添加到您的类路径中。 Maven <…...

深度学习超参数调整介绍
文章目录 深度学习超参数调整介绍1. 学习率2. 批大小3. 迭代次数4. 正则化5. 网络结构总结 深度学习超参数调整介绍 深度学习模型的性能很大程度上取决于超参数的选择。超参数是指在训练过程中需要手动设置的参数,例如学习率、批大小、迭代次数、网络结构等等。选择…...
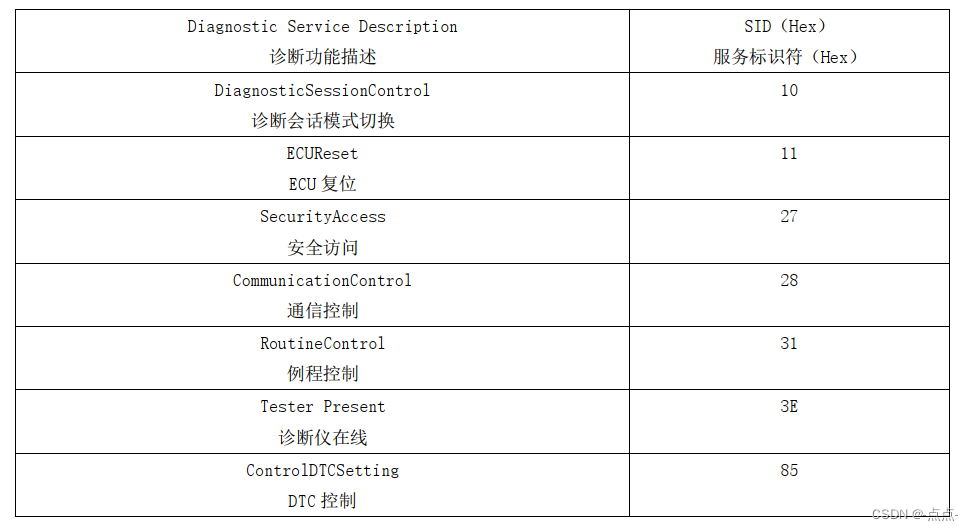
Bootloader
本篇不作太过的技术了解,仅可作为初学者的参考。用嘴简单的语言讲清楚一件事。 项目中遇到Bootloader升级MCU,我很好这是什么软件,逻辑是什么,怎么升级的。 术语及定义 指纹信息fingerprint诊断仪用于标识特定的下载尝试的信息 …...

安卓开发_广播机制_广播的最佳实践:实现强制下线功能
安卓开发_广播机制_广播的最佳实践:实现强制下线功能 ActivityCollector类用于管理所有的ActivityBaseActivity类作为所有Activity的父类创建一个LoginActivity来作为登录界面布局LoginActivity 在MainActivity中加入强制下线功能布局MainActivity在BaseActivity中注…...
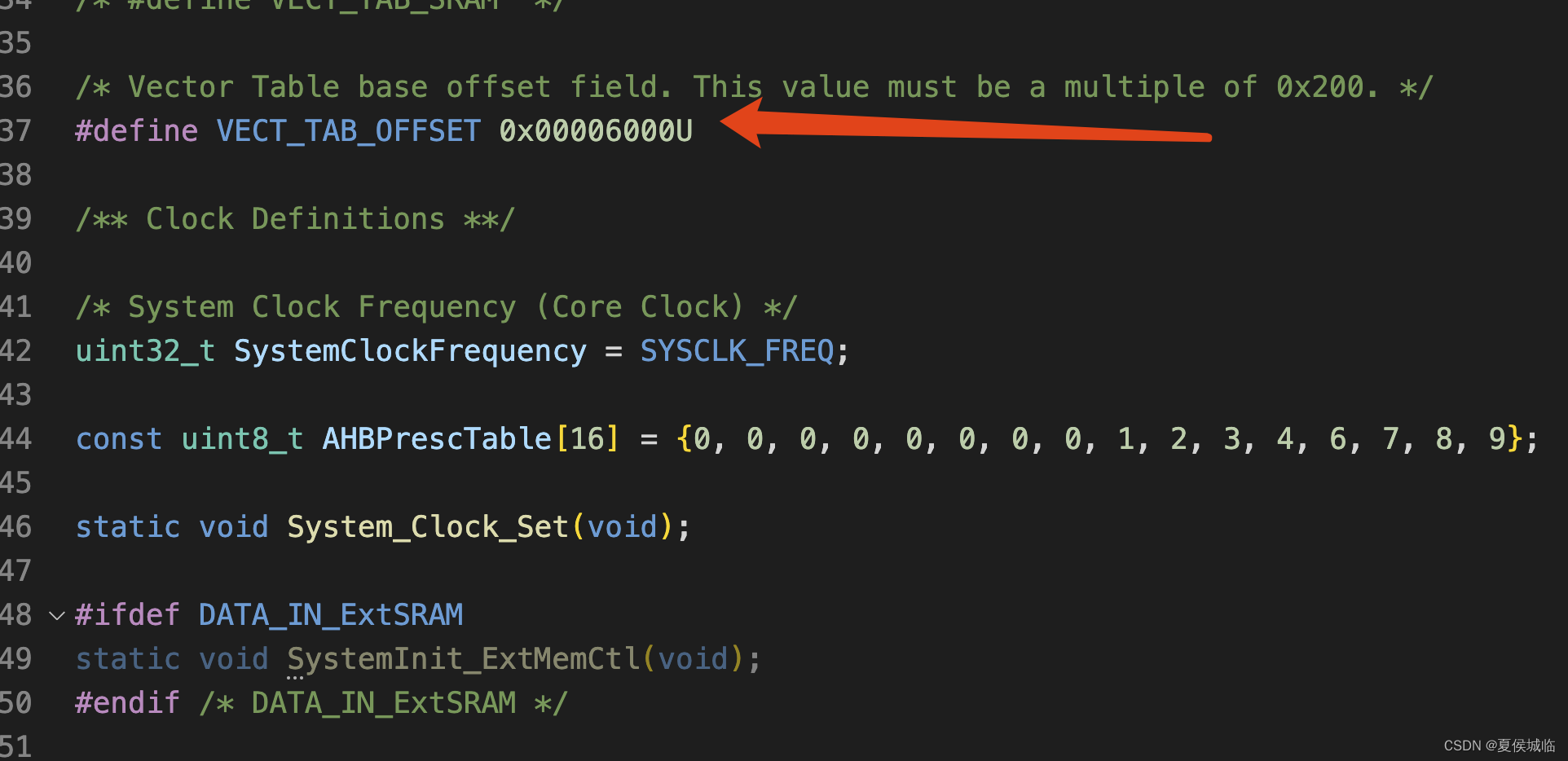
国民技术N32G430开发笔记(10)- IAP升级 Application 的制作
IAP升级 Application 的制作 1、App程序跟Bootloader程序最大的区别就是, 程序的执行地址变成了之前flash设定的0x08006000处, 大小限制为20KB 所以修改Application工程的ld文件 origin 改成 0x08006000 length 改成0x5000 烧录是起始地址也要改为x0x…...

[计算机图形学]材质与外观(前瞻预习/复习回顾)
一、图形学中的材质 不同的物体表面有着不同的材质,而不同的材质意味着它们与光线的作用不同。那么我们之前在介绍辐射度量学和渲染方程提到过其中一个函数,叫做BRDF,而在实际上,也就是BRDF定义了不同的材质。BRDF决定了光如何被反…...
Java 的简要介绍及开发环境的搭建(超级详细)
图片来源于互联网 目录 | CONTENT Java 简介 一、什么是 Java 二、认识 Java 版本 三、选择哪个版本比较好 搭建 Java 开发环境 一、下载 Java 软件开发工具包 JDK 二、配置环境变量 自动配置 手动配置 三、下载合适的 IDE IntelliJ IDEA Visual Studio Code Eclip…...

每天一道算法练习题--Day15 第一章 --算法专题 --- -----------二叉树的遍历
概述 二叉树作为一个基础的数据结构,遍历算法作为一个基础的算法,两者结合当然是经典的组合了。很多题目都会有 ta 的身影,有直接问二叉树的遍历的,有间接问的。比如要你找到树中满足条件的节点,就是间接考察树的遍历…...

golang - 函数的使用
核心化编程 为什么需要函数? 代码冗余问题不利于代码维护函数可以解决这个问题 函数 函数:为完成某一功能的程序指令(语句)的集合,称为函数 在 Go 中,函数分为:自定义函数(自己写…...

真题详解(极限编程)-软件设计(六十一)
真题详解(二分查找平均值)-软件设计(六十)https://blog.csdn.net/ke1ying/article/details/130417464 VLANtag属于 数据链路层实现。 数据链路层:网桥交换机。 网络层:路由器。 物理层:中继器。 Telent…...

计算机网络笔记:TCP粘包
默认情况下, TCP 连接会启⽤延迟传送算法 (Nagle 算法), 在数据发送之前缓存他们. 如果短时间有多个数据发送, 会缓冲到⼀起作⼀次发送 , 这样可以减少 IO 消耗提⾼性能。 如果是传输⽂件的话, 那么根本不⽤处理粘包的问题, 来⼀个包拼⼀个包就好了。但是如果是多条消息, 或者…...

Vue(标签属性:ref、配置项:props、混入mixin、插件、样式属性:scroped)
一、ref(打标识) 前面提及到了标签属性:keys 这里将了解ref:打标识 正常布置脚手架并创建入口文件main.js,引入组件 1. 可以给元素注册引用信息(获取真实DOM) 给一个按钮获取上方的dom的方法,方…...
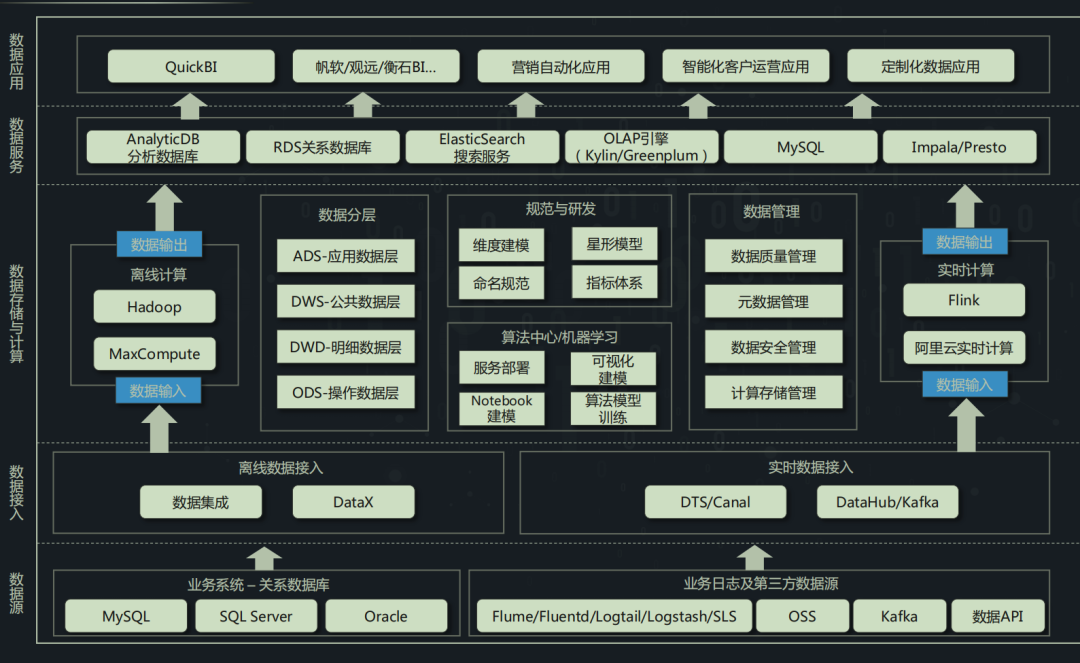
数仓建设规划核心问题!
小A进入一家网约车出现服务公司,负责公司数仓建设,试用期主要一项 OKR是制定数据仓库建设规划;因此小 A 本着从问题出发为原点,先对公司数仓现状进行一轮深入了解,理清存在问题,然后在以不忘初心原则提出解…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
